非标准有限差分法求解一类Burgers-Fisher方程
2019-12-20张艳敏
张 艳 敏
(青岛理工大学 琴岛学院, 山东 青岛 266106)
扩散方程在非线性研究领域占据非常重要的地位,在生物学、力学、物理等领域均有重要作用[1-3].而非线性Burgers-Fisher方程是描述流体动力学中非常重要的模型之一.很多学者对这个方程各种性质和解进行了研究[4-6].比较于线性Burgers-Fisher方程而言,非线性Burgers-Fisher方程更难得到其解析解,或者解析解中含有特殊函数,计算非常麻烦.所以研究对其进行数值求解是很有必要的.目前常采用的数值求解方法主要有有限差分法、插值法等方法[7-9].
本文利用非标准有限差分法(NSFD)[10-13]研究非线性Burgers-Fisher方程. 利用NSFD构建的非标准有限差分格式比较于传统有限差分格式具有更好的动力学行为. 同时给出了差分格式稳定性的条件, 并且对数值解和数值误差的特征进行分析, 最后通过数值算例验证方法的有效性.
本文将研究如下非线性Burgers-Fisher方程
ut-ux+uux=uxx+u(1-u).
(1)
其中,u=u(x,t),(x,t)∈(0,L)×(0,T].
初、边界条件为
式中,L、T为给定的正数,φ(x),φ0(t),φ1(t)为连续函数.
1 预备知识
Mickens在文献[14]中讨论了非线性反应-对流方程
ut+ux=u(1-u),
给出了一个非标准有限差分格式
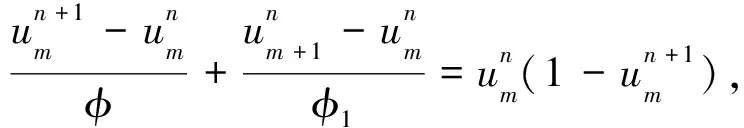
(4)
式中,φ(Δt)=eΔt-1,φ1(h)=eh-1.
式(4)具有如下特征:
1) 取Δt=h,建立了空间步长和时间步长的关系;
2) 导数项离散后的分母是关于步长Δt,h的函数;
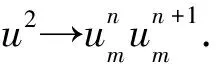
Mickens[15]172-173讨论了对流-扩散方程
ut+ux=buxx,b>0,
给出了一个非标准有限差分格式
(5)
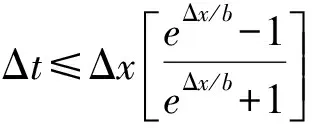
Mickens[15]178-179讨论了非线性扩散方程
ut=uuxx+λu(1-u),
利用子方程法给出了一个非标准有限差分格式
并讨论了式(6)的稳定性.
张蕾在文献[16]中讨论了Burgers-Fisher方程
ut+uux=uxx+λu(1-u),
给出了一个非标准有限差分格式

2 非标准有限差分格式构造

初始条件:

(9)
边界条件:

(10)
式中,φ(Δt)=eΔt-1,φ1(h)=2(eh/2-1),φ2(h)=(eh-1),Ψ=sin2h.
式(8)即为式(1)的非标准有限差分格式.
注2 分母函数φ,φ1,φ2,Ψ均为步长的函数.
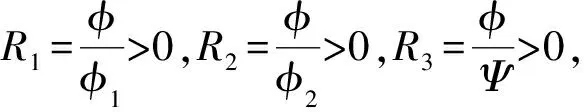


传统的有限差分格式为
3 差分格式数值解与数值误差的特征
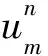


(13)
即满足
得
R1+R2+2R3≤2,
(14)
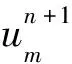
用数值表达式(11)的分子减去分母的一部分项得到
当
1-R1-R2-2R3≥0⟹R1+R2+2R3≤1,
(16)
由式(15)、式(16)得
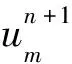
结合式(14)、式(16)得,当R1+R2+2R3≤1时,定理成立.
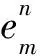
根据定理1的证明过程,定理2显然成立.
4 稳定性与收敛性的证明
引理1[17](Lax等价定理)给定一个适定的初值问题以及与其相容的差分格式,则差分格式的稳定性是收敛性的充分必要条件.
引理2[18-19]差分格式(11)的右端项为非负时,差分格式是稳定的.
定理3 当Δt≤ln(1+h(eh-1))时,式(11)稳定.
证明 根据定理1的证明,当R1+R2+2R3≤1,即可以保证式(11)右端项均为非负,即
(17)
对式(17)进一步整理
稳定性得证.
根据引理2,差分格式也是收敛的.
5 数值算例
考虑如下定解问题
初始条件:
u(x,0)=e-x,x∈(0,1).
边界条件:
u(0,t)=et,u(1,t)=et -1,t∈(0,1].
该问题的精确解为u(x,t)=et -x.取h=0.1,Δt≤ln(1+h(eh-1))≤0.010 462.取Δt=0.01,满足定理1的条件.计算数值解的相对误差见表1.

表1 数值解相对误差Table 1 The relative error of numerical solutions
利用传统的有限差分格式(12)对上述算例使用与式(11)相同的时间和空间步长进行计算.当计算到第16层,即n=16时,数值解就达到了1043数量级,说明数值计算格式(12)是不收敛的.即非标准有限差分格式(11)对时间和空间步长的使用条件更广泛,稳定性与收敛性更好.
从表1可以看出,利用非标准有限差分法求解此类方程精度较高,差分格式数值解和数值误差具有很好的适定性,因此该方法在求解此类方程时是一个有效的方法.
6 结 论
1) 对于非线性项,利用非局部离散方式可以保持差分格式的收敛性与稳定性.
2) 导数项离散后的分母利用步长函数进行逼近可以提高数值精度.
3) 非标准差分格式数值解与原微分方程解析解可以保持相同的动力学行为.
