基于国外技术研究方法的弯道驾驶行为特征统计分析

宋敏

（长春汽车工业高等专科学校，长春 130013）

1 前言

过去10年，通过大数据对驾驶员的驾驶行为进行分析和建模已经成为一个活跃的研究领域。如何使自动驾驶车辆具有类人操作特性，适应复杂驾驶场景并与其他道路使用者进行合理互动，是目前研究的热点。为实现这一目标，通常需要在分析大量自然驾驶数据的基础上，理解和发现驾驶员在驾驶过程中的重要行为特征。

国外科研人员利用自然驾驶数据集开展驾驶员行为方面的研究早于我国[1-4]。美国公路战略研究计划二期项目（Strategic Highway Research Program 2，SHRP 2）共采集了不同年龄段2 800 多名志愿驾驶员超过53 100 000 km 的自然驾驶数据，研究驾驶员的表现和行为在交通安全中的作用，以及如何影响碰撞风险[5]。W.Wang 等利用高斯核密度估计方法，采用相对熵评估2个具有不同数据量数据集的密度函数间的相似度，提出捕捉驾驶员行为基本特征的通用评估方法[6]。朱西产等利用中国大型实车路试项目（China Field Operational Test，China FOT）自然驾驶数据集对驾驶员行为特征、危险工况等进行了广泛、深入的研究，成果应用于自动驾驶控制策略和测试场景开发[7-10]。

弯道行驶是典型的自然驾驶工况，需驾驶员同时控制方向和车速，协调横摆角速度、侧向加速度与弯道曲率的关系。为设计具有类人驾驶行为方式和决策能力的自动驾驶或驾驶辅助系统，应了解该过程的驾驶员行为特征。

文献[11]基于驾驶模拟器研究了弯道行驶过程中驾驶员的速度控制和车道位置选择；文献[12]基于自然驾驶数据集研究了道路曲线形状对驾驶员行为的影响；文献[13]表明车辆侧向加速度是弯道行驶过程中速度选择的关键因素；文献[14]通过对自然驾驶数据的研究发现，弯道行驶过程中最大侧向加速度发生在入口处；文献[15]利用自然驾驶数据集研究了驾驶员如何调整行为以适应车速限制和道路几何形状；文献[16]对全工况自然驾驶数据的研究表明，驾驶员的纵向加速度与侧向加速度分布在双三角形区域内。

驾驶员行为受周围环境和驾驶员自身不确定性的影响很大，但在长时间的驾驶过程中，单个驾驶员的驾驶行为统计特征将趋于稳定。对驾驶员自然驾驶过程长时间采集得到的自然驾驶数据集可以提供真实可靠的、能够表征驾驶员特征的驾驶行为数据。借鉴国外先进研究方法，本文针对弯道行驶场景，分析驾驶员在弯道行驶过程中的行为特征参数的分布特性与相互关系。

2 自然驾驶数据集

本文使用的自然驾驶数据集来自纯电动汽车，共21 位驾驶员驾驶车辆，试验数据采集时间范围为2018年3月19日～2018年10月25日，总行驶里程80 864 km，数据记录时长2 307 h。以10 Hz频率采集了GPS位置、驾驶员操作信号、车辆响应信号等数据。车辆行驶道路主要为城市主干道、城市快速路及高速公路，行驶区域为长春、成都、上海、厦门等10个城市。

3 弯道工况识别

分析弯道工况驾驶员行为特征，首先要准确确定弯道行驶过程。由于自然驾驶数据集中未记录高级驾驶辅助系统（Advanced Driving Assistant System，ADAS）的传感器数据，采用文献[17]提出的方法，利用车辆状态信号对弯道过程进行识别。

根据车辆动力学原理，与直线行驶相比，转弯时车辆航向角、横摆角速度和侧向加速度发生明显变化。考虑到转向盘转角信号随车速变化较大，且由于转向间隙引起的信号误差较大，利用横摆角速度信号进行弯道识别。根据弯道工况的统计分析结果，确定弯道工况辨识逻辑的各项判定阈值，辨识逻辑如图1所示。

其中任意时刻t的航向角φ(t)通过横摆角速度w对时间τ积分计算得到：

式中，t0为开始时刻。

为了验证弯道工况辨识逻辑的准确性，利用车辆GPS 信号绘制车辆运动轨迹，标出已辨识出的弯道工况，辨识结果如图2所示。对150个弯道识别结果进行验证，识别准确率为98.6%。

图1 弯道工况辨识逻辑

图2 弯道工况辨识逻辑验证

利用自然驾驶数据集，共识别得到有效弯道行驶工况29 571个。弯道行驶工况航向角变化如图3所示，弯道航向角可分为4种情况，即φ∈[10°,70°)、φ∈[70°,145°)、φ∈[145°,210°)、φ∈[210°,400°]，分别对应不同的日常驾驶场景，如快速路或高速公路弯道、城市道路路口转弯、180°掉头行驶及高架桥匝道等。航向角的弯道行驶工况占所有弯道行驶工况总数的54%，可能原因是数据集中快速路及高速公路行驶数据比例较高。航向角φ∈[70°,145°)行驶工况占总数的90%，远高于其他2 种弯道行驶工况，这也与日常的实际驾驶经验相符。

4 驾驶行为特征参数分布的收敛性

为了准确描述驾驶行为特征参数的概率分布特性，首先需确定当前数据集数据能否得到稳定收敛并真实可信的驾驶行为特征参数的概率分布结果。数据量不足可能导致无法得到准确的分析结果，过多的数据则会浪费数据采集资源。针对这一问题，文献[6]提出了一种基于高斯核密度估计的驾驶员行为综合评价方法，应用相对熵测量不同数据量的密度函数之间的相似性，本文基于文献[6]中提出的方法，讨论基于自然驾驶数据集的驾驶行为特征参数概率分布收敛性。首先，使用核密度估计得到不同加速度分布数据量数据集的驾驶行为特征参数的概率分布；其次，使用相对熵来衡量各数据集核密度估计间的差别；最后，根据相对熵的变化确定能够得到稳定收敛驾驶行为特征参数概率分布的数据量，确定当前数据集能否满足分析要求。

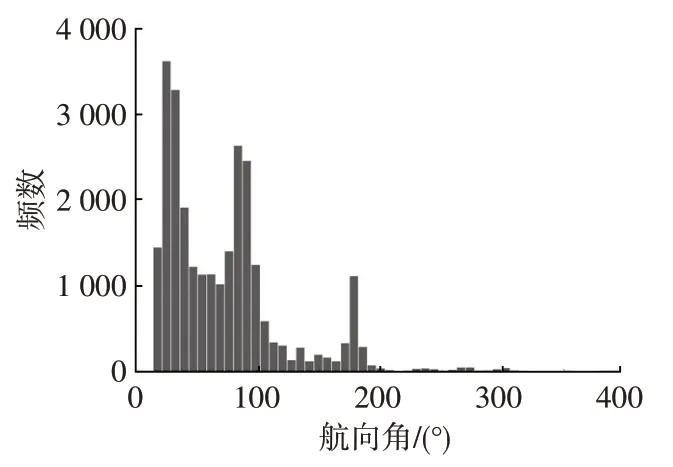
图3 弯道过程航向角分布

由于驾驶员行为数据不能通过传统的分布函数（正态分布、泊松分布、指数分布等）进行拟合，也就无法通过概率密度函数对特征分布进行表达。研究表明，通过多元高斯混合模型（Gaussian Mixture Model，GMM）可以描述驾驶行为特征[18]。核密度估计（Kernel Density Estimation，KDE）是概率论中用来估计未知密度函数的方法。利用高斯混合模型和核密度估计等非参数方法可以通过有限的数据采样点来拟合驾驶员的行为特征分布。

记xi为一组观测向量，多维核密度函数定义为：

式中，K(x)为核函数；x为任意一组观测向量；n为观测数据的数据量。

选择多维高斯函数作为核密度估计的核函数，则核函数可以表示为：

式中，d为观测数据维数；H为d×d维的带宽矩阵，使用文献[19]中的方法进行估计；|H|为矩阵H的行列式。

相对熵（Relative Entropy）又被称为Kullback Leibler散度或信息散度，是2个概率分布间差异的非对称性度量，可用于描述2 个概率分布之间差异的大小，当一组新的数据加入到原有数据集后，可以使用相对熵来检验原数据集与新数据集之间是否存在显著差异。记一组新数据的数据量为m，原数据集的数据量为n，则新数据集的数据量为(n+m)，2个数据集的相对熵定义为：

对纵向加速度和侧向加速度联合分布数据进行分析，结果如图4 所示。当相对熵DKL＜ϵ ∙（ϵ为判断阈值）时，认为2个数据集之间的相对熵趋于稳定，本文设ϵ=0.001。随着样本数量的增加，相对熵变化情况如图5 所示，当分析样本数量达到25×105个时，满足收敛条件。本文提取到的弯道行驶样本数量为5 078 649个，能够获得稳定收敛的驾驶行为特征参数概率分布。

图4 纵向加速度与侧向加速度联合分布

图5 相对熵随样本数量变化曲线

5 驾驶行为特征分布特性及应用

弯道行驶过程中，驾驶员根据道路曲率，考虑车辆动态响应和运动极限，通过调整转向盘、油门踏板和制动踏板控制车辆。车速、侧向加速度、纵向加速度及横摆角速度通常显著变化，并存在耦合关系。其中，侧向加速度与纵向加速度通过附着椭圆相互影响，侧向加速度、纵向加速度、横摆角速度通过圆周动力学相互影响。

5.1 纵向加速度与侧向加速度的关系

纵向加速度和侧向加速度联合分布的分位曲线如图6所示。其中，纵向加速度的正、负分别表示驱动加速及制动减速过程，侧向加速度的正、负分别表示左、右转弯，侧向加速度在左、右转弯过程中没有显著区别。随着驱动加速度或制动减速度的增加，侧向加速度减小；侧向加速度较大时，纵向加速度较小，说明车辆以较大侧向加速度通过弯道时，驾驶员通常选择保持车速稳定。

图6 纵向加速度和侧向加速度联合分布不同百分位统计

从联合分布数据中可以看出，弯道行驶过程中，车辆通常达不到附着极限。对第99 百分位曲线进行拟合，可以认为，在联合分布坐标系中，纵向加速度和侧向加速度分布在由(3.3 m/s2,0 m/s2)、(-0.3 m/s2,3.9 m/s2)、(-4.0 m/s2,0 m/s2)、(-0.2 m/s2,-4 m/s2)4 个点控制的四边形区域内，这一结论与文献[9]基本相同。由于本文对弯道行驶场景进行分析，得到的四边形区域沿侧向加速度方向对角线较长。

5.2 车速对侧向特征的影响

车速与侧向加速度的关系如图7 所示。在10～40 km/h 车速区间，随着车速增加，侧向加速度缓慢增大；在＞40～50 km/h车速区间，驾驶员通常选择较大侧向加速度；在＞50～80 km/h车速区间，侧向加速度随车速逐步减小；车速超过80 km/h后，侧向加速度随车速缓慢增大，可能原因是车辆行驶在快速路或高速公路上，道路曲率一定时，随车速的增加，侧向加速度增大。

图7 车速与侧向加速度的关系

车速与侧向加速度第99.9 百分位曲线可以认为是自然驾驶的极限情况，车速小于60 km/h时，侧向加速度基本超过3.5 m/s2。为保证行驶安全性和舒适性，自动驾驶或驾驶辅助系统开发时，车辆的最大侧向加速度应控制在第99.9百分位线以内。

车速与横摆角速度的关系如图8所示。由图8可以看出，在0～15 km/h低速区间范围，随车速的提高，横摆角度最大值线性增大，这种状态是由于车辆低车速掉头行驶时，转向盘处于极限位置造成的。车速超过15 km/h以后，横摆角速度随车速升高而减小，车速大于100 km/h时，横摆角速度趋于稳定而略有增大。

图8 车速与横摆角速度的关系

在低车速区间，驾驶员通常选择较大横摆角速度，以提高车辆的通过性；在高车速区间，不同百分位曲线较为接近，说明在转弯过程中，横摆角速度通常维持在相对稳定的区间范围内。

5.3 最大侧向加速度与曲率半径的关系

为了分析弯道行驶过程中的稳态操作行为，对弯道行驶最大侧向加速度（不区分左转与右转）与曲率半径进行分析。弯道行驶过程中，根据不同的弯道曲率，驾驶员以侧向加速度为预瞄目标，调整车辆行驶速度，以合适的侧向加速度通过弯道。

弯道过程最大侧向加速度与曲率半径的关系如图9 所示，在小曲率半径（0～200 m）区域，最大侧向加速度随曲率半径增加迅速减小，随后最大侧向加速度随曲率半径增加缓慢减小。曲率半径较大时，受车辆响应及附着极限影响，驾驶员通常选择较小的侧向加速度通过弯道。其中，第99 百分位曲线可以用于高速自适应巡航系统在弯道行驶过程中极限情况下车速选择的参考。

图9 弯道过程最大侧向加速度与曲率半径的关系

5.4 驾驶行为特征分布应用

自动驾驶汽车应具有类人的驾驶能力，弯道过程驾驶行为特征分布特性可用于自动驾驶汽车的驾驶能力测试。通过自动驾驶汽车获得在真实驾驶场景下的弯道驾驶行为数据，确定其驾驶行为特征分布，并与本文得到的驾驶行为分布特征进行对比，二者越符合，表明自动驾驶汽车在弯道行驶中的行为与人类驾驶员越相似。

根据驾驶员的驾驶行为特点，人类驾驶员表现出不同的驾驶风格，如追求速度的运动型驾驶员、追求舒适的平稳型驾驶员等。对于自动驾驶汽车或驾驶辅助系统，同样应具有不同的风格，以满足不同人群的需求。根据自然驾驶数据集获得的弯道驾驶行为特征分布，选择不同的百分位曲线，用于自动驾驶汽车及驾驶辅助系统控制目标设定，可在相同驾驶条件下，使自动驾驶汽车的驾驶行为体现出差异性。

6 结束语

本文利用自然驾驶数据集研究了弯道行驶过程中驾驶员行为特征的统计特性。利用动力学方法识别车辆弯道行驶工况，利用核密度估计及相对熵描述不同数据集间驾驶行为特征参数概率分布的差异。对驾驶行为特征参数的分布特性进行分析，结果表明：纵向加速度与侧向加速度存在明显的耦合关系，但未达到附着极限，分布在四边形区域内；在40～50 km/h车速范围，驾驶员通常选择较大的侧向加速度；在低车速区间，横摆角速度变化更为剧烈；弯道过程最大侧向加速度随道路曲率半径增大而降低，在小曲率半径区间下降更为迅速。弯道驾驶行为特征分布可用于自动驾驶汽车类人驾驶能力评价，自动驾驶或驾驶辅助系统选择不同的百分位曲线作为控制目标及边界，可以实现不同的驾驶风格。