求解散射问题中消除多次透射边界飘移失稳措施的效果分析

唐晖　李小军

摘要：针对应用多次透射人工边界公式求解散射问题时可能出现的飘移失稳现象，对比分析了实时降阶法、修正算子法、附加黏弹器法和改进输入法的消飘效果和对计算精度的影响，结果表明：4种方法均可有效消除或抑制比较缓慢的飘移失稳现象;飘移趋势强烈时，修正算子法和附加黏弹器法可能无法有效地抑制失稳;当阻尼较小时，采用实时降阶法可能引入额外的低频误差;在能够确定适当参数值的前提下，修正算子法和附加黏弹器法能够提高低频计算精度;改进输入法则无需人为设置参数，能够在抑制飘移失稳的同时提高计算精度。

关键词：多次透射人工边界公式;飘移失稳;消飘措施

中图分类号：P315.9 文献标志码：A 文章编号：1000-0666（2019）04-0493-10

0 引言

多次透射人工边界（MTF）是由Liao和Wong（1984）提出的可具有N阶精度的局部人工边界条件，其基本思想是直接模拟外行波穿过边界的过程，通过与边界点相邻的内部点在现在时刻以及前几个时刻的运动给出边界点在下一时刻的运动量。这种时空解耦的边界条件不仅物理意义清晰，且易于在数值离散计算中实现，良好的普适性、灵活性以及计算效率等方面的明显优势使其能够在求解复杂问题中发挥积极的作用，得到广泛应用（杨光，刘增武，1994;李小军等，1995;金星等，2004;丁海平等，2006;孔戈等，2007;徐建平等，2008;陈少林等，2010;卢再华等，2010;唐晖等，2012;李铁飞等，2013;方宏远，林皋，2013）。

与其它局部边界相同，该边界条件在应用中也存在稳定性问题，这也一直是人们关注的重要问题。为了消除或抑制多次透射人工边界可能引入的飘移失稳，李小军和廖振鹏（1996）首先针对散射问题探讨了低频飘移现象的形成机制，指出入射波场采用连续介质解析解与离散模型中实际入射波之间的差别会导致低频飘移失稳，并给出了计算过程中实时降低透射阶数以稳定计算的建议;周正华和廖振鹏（2001，2004）基于双曲型偏微分方程数值解稳定性GKS准则给出飘移失稳的另一个解释，即多次透射人工边界无法阻止波动中的零频成分进入计算区域，提出了在多次透射人工边界公式中加入修正算子的消除漂移失稳措施;李小军和杨宇（2012）尝试在边界施加黏弹性组件来抑制飘移失稳;唐晖等（2016）给出了一种改进的波动输入方法，即通过划分边界区，计算获得入射波场的数值解以实现波动输入，从而减小入射波场采用解析解引入的误差以消除或抑制低频飘移现象。

实际工程中采用何种消除飘移失稳措施（后文简称消飘措施），除了考虑其能否在计算时间内消除或抑制飘移失稳现象，还须考量所采用方法对于计算精度的影响，尤其是对低频响应较为敏感的长周期结构等。鉴于此，本文针对利用多次透射人工边界求解如构筑物抗震分析等波动散射问题时可能出现的飘移失稳现象，综合对比分析实时降阶法、修正算子法、附加黏弹器法和改进输入法在消除飘移失稳方面的效果和对计算结果精度的影响，以期为多次透射人工边界条件在工程中应用提供有益的参考。

1 飘移失稳机制

对于采用多次透射人工边界时出现的飘移失稳机制有2种：一种是从透射边界公式本身出发，另一种是针对利用多次透射人工边界求解散射问题的情况。

第一种（周正华，廖振鹏，2001，2004）定义传递因子为Bmn，传递函数为：

式中：upj代表计算区域内与边界相距jcaΔt、处在时刻pΔt的位移，其中ca为人工波速，Δt为离散时间步距;j，p，m和n均为任意非负整数，将N阶透射人工边界公式表示为：

依据GKS准则，计算中不出现飘移失稳的充分条件为：任何满足内域内行波的波动解，不同时满足边界条件。那么，对于满足内域的弹性波动解为：

将式（3）代入式（2）可以得到多次透射边界不飘移失稳的条件：

然而，对于零频和零波数，即ω=k=0的波动成分时，式（4）不成立，即零频成分可以从多次透射人工边界条件进入计算内域，从而引起飘移失稳。谢志南（2014）利用模态分析法进一步分析了相应的飘移失稳机制，并在此基础上结合Z变换解释了零频飘移失稳数值解的增长模式。

另一种，李小军和廖振鹏（1996）指出在求解散射问题时，为了利用透射边界模拟外行波，地震波动输入过程中需要将总波场分离为入射波场和外行波场：

U=Ui+Us（5）

式中：U，Ui和Us分别代表总波场、入射波场和外行波场。然而，离散网格中实际入射波场不易获得，往往采用解析解，其与真实入射波场之间存在一定差别，公式如下：

式中：Uci，Ucs和ΔU分别代表计算中的入射波场、外行波场以及计算入射波场和真实入射波场之间的误差。将式（6）（7）代入式（5）可以得到：

即透射边界模拟的外行波不仅包含真实的外行波Us，还包含了入射波场误差ΔU，这会导致飘移失稳现象的产生。

2 消飘措施

2.1 实时降阶法

李小军和廖振鹏（1996）指出由于入射波场引入的误差会导致飘移失稳趋势的出现，并且证明了当外行波场出现式（9）和（10）的失稳趋势时，利用二次及二次以上透射公式时，计算飘移失稳趋势将会继续，即高阶透射公式将可能引起计算飘移失稳现象：

式中：upJ-i表示在时刻pΔt、计算区域内垂直于边界并距离边界节点J的第i个节点（i=0，1，…，m）的外行波位移。基于此，李小军和廖振鹏（1996）给出了实时降低透射阶数以消除飘移失稳的方法，在计算过程中对边界点和对应的区域内m個节点进行实时监测，一旦满足如式（9）和式（10）给出的条件，则之后的n个计算步均采用一阶透射公式。

2.2 修正算子法

基于飘移失稳机制的第一种解释，周正华等（2001，2004）针对边界条件式（2）进行了修改：

式中：γ是任意小正数。

将式（3）代入式（11）得到对于任何频率均可满足的条件式：

2.3 附加黏弹器法

李小军和杨宇（2012）尝试在边界区节点施加黏弹性元件，以约束边界区域不合理位移，从而消除高频或飘移失稳趋势向计算内域的延续。该方法将边界区内包括边界点J在内的边界法向上2N个节点（N阶透射公式）的动力方程定义为：

式中：[M]为质量矩阵;[K′]和[C′]分别为对体系固有的刚度矩阵[K]和阻尼矩阵[C]进行修正后的阻尼矩阵和刚度矩阵：

式中：k0和c0为附加弹簧的剛度系数和附加阻尼器的阻尼系数。

2.4 改进波动输入法

基于消除或减小所采用的入射波场与有限元网格中的实际入射波场的差别，从而消除或抑制飘移失稳现象的思路，唐晖等（2016）给出了改进波动输入的方法，尝试利用多次透射人工边界条件获得网格中实际入射波场用于波动输入中。该方法无需根据试算或经验设定参数，计算方便并能提高计算精度。

3 消除飘移措施分析

如上文所述，在应用多次透射公式求解实际工程问题，尤其是对低频成分敏感的构筑物地震响应时，不仅要关注所采用的消飘措施能否有效消除或抑制失稳现象，还须关注其对计算精度的影响。因此，下文将对这2方面开展对比分析。需要特别说明的是，波动有限元中瑞利阻尼的质量系数使得零波数及邻近波动对应为非行进波，但该数值对计算稳定性影响较小，而刚度系数使得行波的衰减随波数增大而增大，能够抑制高频失稳（章旭斌，谢志南，2017），因此，下文分析中仅考虑瑞利阻尼的刚度系数。

3.1 消飘措施效果分析

3.1.1 算例一

如图1所示的均匀水平地表场地，有限元模型尺寸为L=300 m、H=100 m，网格尺寸为2 m×2 m，S波波速为2 100 m/s，瑞利阻尼刚度系数β=0.001，如图2所示的SH波位移脉冲以角度θ=45°入射，采用二阶透射人工边界。

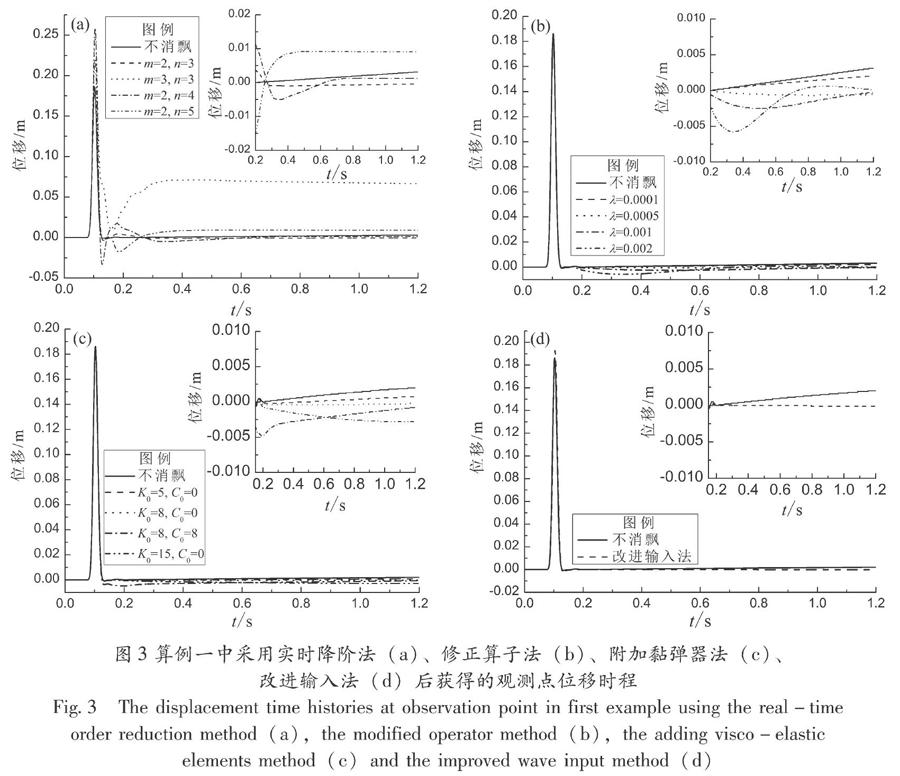
当采用实时降阶法时，式（9）或（10）中用于判断失稳趋势的节点数和连续使用一阶透射的时间步数，即参数（m，n）分别为（2，3）（3，3）（2，4）和（2，5），计算所得地表观测点的位移时程如图3a所示，本算例中飘移失稳趋势较为缓慢。如何设置用于判断失稳趋势的节点数和连续使用一阶透射的计算步数对于消飘效果会产生显著影响，其中（m，n）为（2，3）的消飘效果较好，而一阶透射计算步数增加为4和5时，计算误差随之增加，在计算时间内无法有效抑制低频飘移，当m=3时，即基于边界法向上包括边界节点在内的4个节点判断失稳时，计算结果会出现更明显偏离。

图3b为采用修正算子法获得的计算结果，其中修正算子λ取值分别为0.000 1，0.000 5，0.001和0.002。当λ=0.000 1时，对计算结果影响有限，无法有效抑制飘移现象;λ=0.000 5时，该方法较好地消除了飘移失稳;而λ=0.001和0.002时，给计算结果引入了较大的低频干扰。

采用附加黏弹器法在边界设置附加弹簧和附加阻尼系数分别为（5，0）（8，0）（8，8）和（15，0）时，相应的计算结果如图3c所示，其中附加弹簧和附加阻尼系数为（8，0）时能够有效地消除飘移失稳，与修正算子法类似，其消飘效果依赖于附加弹簧系数和附加阻尼系数取值。

采用改进输入法获得的观测点位移时程如图3d所示，该方法可以有效地抑制低频飘移现象，重要的是，采用该方法不需要依据经验试算设定参数。

3.1.2 算例二

如图4所示的不规则凹陷场地，计算区域尺寸为L=950 m，H=200 m，SH波以30°从左下角入射，其位移时程如图2所示，S波波速2 100 m/s，瑞利阻尼与算例一相同，最小网格为2 m左右。采用实时降阶法，修正算子法，附加黏弹器法和改进输入法获得的观测点位移时程和其频谱曲线如图5所示。与算例一不同，该算例中飘移失稳趋势较为强烈，当m=2以及连续使用一阶透射的次数n为3，4和5时，实时降阶法均能在计算时间内较好地抑制飘移失稳，而m=3时无法抑制或消除失稳现象。修正算子法中修正算子λ分别为0.000 1，0.001，0.002和0.005，修正算子λ越大，对飘移现象的抑制作用越强，但也会给计算结果带来过大的低频干扰，从而失去了应用意义。而边界设置附加弹簧和附加阻尼系数分别为（5，0）（15，0）（30，0）和（30，30）时，与修正算子法相同，无论如何设置黏弹器参数也无法在不过度引入低频误差的前提条件下有效地抑制飘移失稳现象。采用改进输入法后，计算时间内失稳趋势同样得到了很好的抑制。

综上可知，就二阶透射而言，对于失稳现象较为平缓的情况，上述4种方法均能消除或抑制飘移失稳。基于边界内几个点判断失稳趋势以及失稳趋势出现后采用一阶透射时间步数都会对实时降阶法的消飘效果产生影响，二者取值过大可能会给结果引入过多误差，影响消飘效果，建议判断失稳趋势时，式（9）（10）中m和连续使用一阶透射次数n分别取值2和3。修正算子法中修正因子λ如何选取十分关键，其取值过小无法很好地抑制或消除飘移失稳，取值过大则会影响计算精度，尤其是对于低频波动成分，修正算子λ如何取值既能消除失稳又不过多影响计算结果精度。目前除了经验试算仍没有很好的方法，然而，对于一些复杂工程问题往往无法通过经验试算来判断λ取值是否合理。与修正算子法类似，附加黏弹器法亦需要通过经验试算确定。改进的输入法可以有效地消除飘移失稳，并获得合理的计算结果。

与实时降阶法和改进输入法不同，当失稳趋势强烈时，修正算子法和附加黏弹器法可能无法在过多影响计算精度的前提条件下有效地抑制低频飘移失稳。

3.2 消飘措施对计算精度影响分析

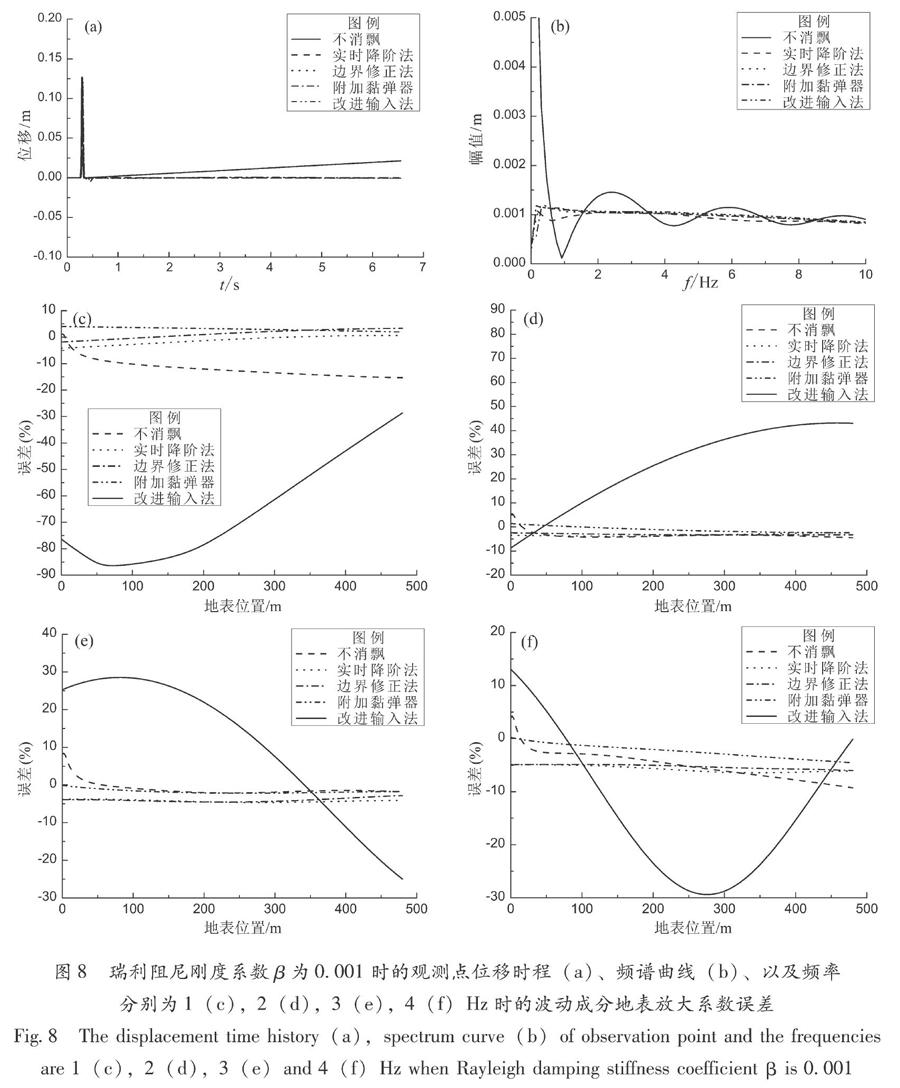
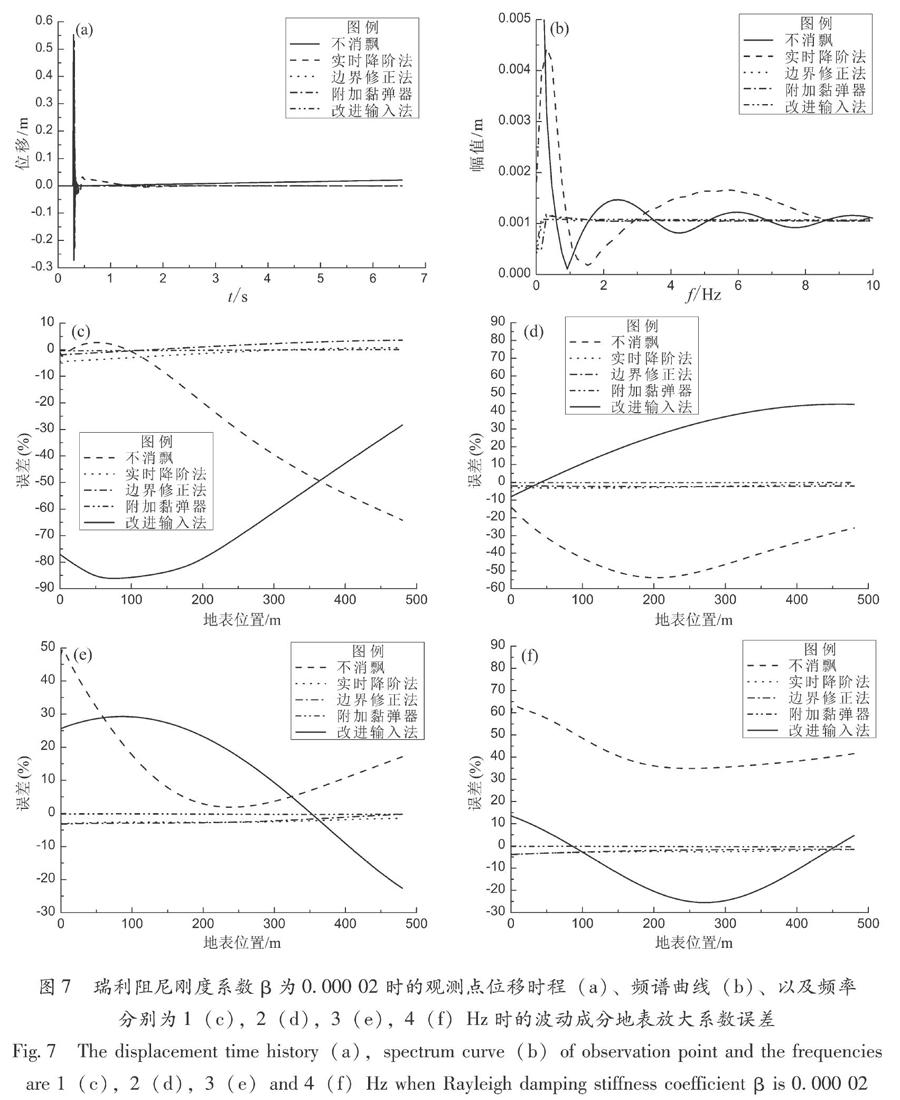
为了对比上述消除低频飘移方法对计算精度的影响，以如图1所示的水平均匀场地为算例，模型尺寸L和H分别为480和200 m，有限元网格亦为2 m×2 m，计算时间步距为0.000 2 s，位移时程如图6所示，SH波从模型左下以45°角度入射。参考算例一的结果，实时降阶法中用于判断失稳的边界内节点数和连续一阶透射计算步数（m，n）为（2，3），修正边界法中修正因子λ=0.000 5，附加黏弹器法中弹簧和阻尼系数为（8，0），在算例一中，4种消飘措施均能抑制飘移失稳现象。瑞利阻尼刚度系数为0.000 02和0.001时，地表观测点的位移时程分别如图7a和图8a所示，其频谱曲线分别如图7b和图8b所示，对于低频波动成分为1，2，3，4 Hz，阻尼可忽略，地表处相对于输入的放大系数可以近似为2，图7c～f和图8c～f则分别给出计算获得的地表放大系数误差。观察输入位移脉冲和计算所得地表观测点的频谱曲线、地表放大系数误差曲线可以看出，当阻尼为0.000 02时，实时降阶法虽然抑制了“零频”飘移，却给低频成分的计算结果引入了更大的误差，而阻尼为0.001时，该方法在抑制失稳的同时提高了低频成分计算精度，这可能是因为低阻尼时高频波动成分丰富，而实时降阶法对这部分波动的计算精度影响较大，误差波在计算区域叠加从而导致了低频误差增加。阻尼大小对其他3种消飘措施的影响较小，这3种方法不仅能够在计算时间内消除“零频”飘移现象，还能提高计算精度，其中，改进输入法对低频计算精度的提高最为明显。

4 结论

本文对比分析了实时降阶法、修正算子法、附加黏弹器法和改进输入法等4种消飘措施的消飘效果和对计算精度的影响。得出以下结论：

（1）对于二阶人工透射边界，就消飘效果而言，当飘移失稳较为缓慢时，实时降阶法、修正算子法、附加黏弹器法和改进输入法均可用于抑制失稳，但是，前3种措施的消飘效果与其参数设置有关。当基于包括边界点在内的3个节点的结果来判断失稳趋势，并在失稳趋势出现后连续使用3

图8 瑞利阻尼刚度系数β为0.001时的观测点位移时程（a）、频谱曲线（b）、以及频率分别为1（c），2（d），3（e），4（f）Hz时的波动成分地表放大系数误差次一阶透射计算步数进行计算时，实时降阶法的消飘效果相对较好。而为了消除失稳的同时不过多影响计算精度，修正算子法中修正算子以及附加黏弹器法中弹簧和刚度系数则需要通过经验试算来确定。然而，对于许多复杂的实际工程往往无法评价参数的选取是否合理，改进输入法不需要人为设置参数，且消飘效果良好。

（2）飘移失稳趋势强烈时，修正算子法和附加黏弹器法可能会引入较大低频误差，从而失去了应用价值。不同于失稳趋势缓慢的情况，实时降阶法在基于包括边界点在内的边界内3节点判断失稳趋势，且连续使用一阶透射次数大于或等于3次时，均能在计算时间内有效地抑制失稳现象。鉴于此，在利用實时降阶法时，建议判断失稳趋势的节点选取包括边界点在内的3个节点，且失稳趋势出现后的3个计算步骤均使用一阶透射;改进输入法则仍能够有效地抑制失稳现象。

（3）当4种措施都能抑制飘移失稳时，即计算出现缓慢的飘移现象时，实时降阶法在阻尼较大时可以提高低频成分计算精度，但是，由于降低透射阶数也就降低了精度，所以，这方面不如另外3种措施，而阻尼较小时，该方法则可能会引起更大的低频误差。在能够确定合适参数的前提条件下，修正算子法和附加黏弹器法可以在抑制低频飘移的同时提高计算精度。改进输入法不仅消飘效果良好，其对计算精度的提高也十分明显，重要的是该方法不需要人为设置参数，应用较为方便。

对于三阶及三阶以上的高阶透射边界，单独采用这4种方法均无法有效地消除或抑制失稳现象，而本文的研究结果提供了将改进输入法和其他措施结合以消除失稳的思路。

参考文献：

陈少林，唐敢，刘启方，等.2010.三维土-结构动力相互作用的一种时域直接分析方法[J].地震工程与工程振动，30（2）：24-31.

丁海平，刘启方，金星.2006.长周期地震动三维有限元数值模拟方法[J].地震工程与工程振动，26（5）：27-32.

方宏远，林皋.2013.基于辛算法模拟探地雷达在复杂地电模型中的传播[J].地球物理学报，56（2）：653-659.

金星，孔戈，丁海平.2004.水平成层场地地震反应非线性分析[J].地震工程与工程振动，24（3）：38-44.

孔戈，周健，徐建平，等.2007.盾构隧道横向地震响应规律研究[J].岩石力学与工程学报，26（增刊1）：2872-2879.

李铁飞，陈学良，高孟潭.2013.盆地场地效应的三维数值模拟研究进展及沉积环境对盆地场地的影响[J].世界地震工程，29（3）：56-68.

李小军，廖振鹏，关慧敏.1995.粘弹性场地地形对地震动影响分析的显式有限元-有限差分方法[J].地震学报，17（3）：232-244.

李小军，廖振鹏.1996.时域局部透射边界的计算飘移失稳[J].力学学报，28（5）：627-632.

李小军，杨宇.2012.透射边界稳定性控制措施探讨[J].岩土工程学报，34（4）：641-645.

卢再华，张志宏，顾建农.2010.透射边界在点声源海底地震波数值计算中的应用[J].应用声学，29（5）：358-363.

唐晖，李小军，李亚琦.2012.自贡西山公园山脊地形场地效应分析[J].振动与冲击，31（8）：74-79.

唐暉，李小军，周国良.2016.散射问题求解中消除多次透射公式漂移失稳的一种措施[J].岩土工程学报，38（5）：952-958.

谢志南.2014.透射边界零频飘移失稳数值解增长模式解释[J].地震工程与工程振动，34（4）：15-20.

徐建平，孔戈，周健.2008.接头形式对联络通道抗震性能影响的研究[J].工程抗震与加固改造，30（2）：57-62.

杨光，刘增武.1994.地下隧道工程地震动分析的有限元-人工透射边界方法[J].工程力学，11（4）：122-130.

章旭斌，谢志南.2017.离散网格中瑞利阻尼对波动的影响分析[J].地震工程与工程振动，37（1）：141-148.

周正华，廖振鹏.2001.消除多次透射公式飘移失稳的措施[J].力学学报，33（4）：550-554.

周正华，廖振鹏.2004.修正算子γB_0^0的物理含义解释[J].地震工程与工程振动，24（5）：17-19.

Liao Z P，Wong H L.1984.A transmitting boundary for the numerical simulation of elastic wave propagation[J].Soil Dynamics and Earthquake Engineering，3（4）：174-183.

Analysis on Measures of Eliminating Drift instability of Multi-transmissionFormula in Solving Scattering Problems

TANG Hui1，LI Xiaojun2，3

（1.Nuclear and Radiation Safety Center，MEP，Beijing 100082，China）（2.College of Architecture and Civil Engineering，Beijing University of Technology，Beijing 100124，China）（3.Institute of Geophysics，China Earthquake Administration，Beijing 100081，China）

Abstract

Abstract：For solving the wave scattering problems with Multi-Transmitting Formula，the effects of the real-time order reduction method，the modified operator method，the adding visco-elastic elements method and the improved wave input method on eliminating drift instability and on computation accuracy are compared and analyzed to provide useful reference for engineering application of this artificial boundary.The results show these four methods can effectively eliminate the relatively slow drift instability phenomenon;when the instability trend is strong，the modified operator method and the adding visco-elastic elements method cannot depress the instability effectively.The low-frequency errors may be introduced by the real-time order reduction method when the damping is small.Under the premise that the values of parameters can be determined appropriately，the modified operator method and the adding visco-elastic elements method can improve the calculation accuracy of low-frequency.The improved wave input method can depress drift instability and improve calculation accuracy without setting parameters artificially.

Keywords：Multi-Transmitting Formula;drift instability;measures of eliminating drift instability