基于特征线法计算的超细群慢化方程求解方法

秦 帅，张 乾,*，赵 强，梁 亮，吴宏春，曹良志

(1.哈尔滨工程大学 核安全与仿真技术国防重点学科实验室，黑龙江 哈尔滨 150001；2.西安交通大学 核科学与技术学院，陕西 西安 710049)

共振自屏计算是反应堆物理计算中的关键环节，它为输运计算提供共振能群的群常数。然而在共振能区，共振核素的各种截面随能量变化十分剧烈，共振区群常数与实际问题的几何、材料、温度等均有着密切的关系。

目前常用的共振计算方法有等价理论[1]和子群方法[2]。其中，等价理论的基本思想是建立起均匀系统和非均匀系统之间的等价关系，算法稳定，计算效率高，工程应用经验丰富，但等价理论中引入了诸如窄共振近似、平通量假设等多种假设或近似，影响了计算精度[3]。子群方法根据截面值的大小将1个较宽的共振群划分为几个子群，利用子群参数来描述截面进入子群的概率。子群方程与中子输运方程在形式上相似，能与各种输运方法相结合[4]，因此子群方法几何适应性好，可很好解决空间效应，但子群方法在处理子群参数时存在数值不稳定性。同时，传统的等价理论和子群方法均不能很好处理共振干涉效应。

超细群共振计算方法的基本思想是对共振区做非常精细的能群划分，建立超细群慢化方程，自上而下依次求解慢化方程，获取超细群结构的中子能谱，进而归并出有效自屏截面。超细群方法是一种严格精确的共振计算方法，可有效计算复杂几何、复杂能谱下的共振问题。1964年，日本原子能研究院开发了第1个具备工程实用价值的超细群共振计算程序RABBLE[5]，一些商业程序如SRAC[6]和AEGIS[7]也采取了超细群方法。此外，国内西安交通大学也开发了超细群共振计算程序UFOP[8]。传统超细群程序采用一维圆柱几何和预制碰撞概率插值表的方法求解慢化方程，但这种方法不具备处理复杂几何的能力，同时预制插值表的维数会随共振材料种类的增加而增加，当插值表维数较高时，预制该表的计算成本无法接受。

随着核能技术的发展，未来燃料栅元和组件的设计趋于复杂，为实现复杂几何、复杂能谱条件下的精细共振计算，本文根据超细群慢化方程理论模型，结合特征线法(MOC)[9]计算，建立基于特征线的超细群慢化方程求解方法，计算一系列复杂问题。

1 理论模型

对于要求解区域，近似认为不考虑裂变源，同时，散射源项也可仅考虑各向同性弹性散射[7]，同时也不考虑上散射[10]。这样，中子慢化方程可写成如下格式：

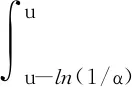
(1)

式(1)右端为慢化方程的散射源项，可写为：

(2)

当考虑一个划分为多区域且包含多种核素的实际问题时，对于1个区域R，式(2)可写为：

(3)

式中：K为核素数；Δk为中子与核素k发生碰撞后所能获得的最大对数能降。

将共振能区划分为非常精细的能群，称为超细群，为保证中子在1个超细群所包含的能量范围内只发生1次碰撞，超细群的能群宽度应远小于中子与最重的核素发生1次碰撞后所能获得的最大对数能降。为方便计算，将所有超细群的宽度设为相同值，对于某个超细群g，式(3)可写为：

(4)

式中：Lk为中子与核素k发生1次碰撞后有可能穿过的最大能群数，Lk=-lnαk/Δuf；Pnk为中子与核素k发生1次碰撞后穿过n个能群进入g群的概率；Δuf为超细群的能群宽度。由于中子在1次碰撞后有可能穿过的能群数过大，直接求解式(4)会非常耗时，文献[11]给出了Qg的递推关系式：

(5)

对于式(5)的递推关系，首先需计算超细群首群的散射源，而超细群首群的慢化中子来源于共振求解区域以上的能量段，在共振能区以上，截面随能量的变化较平缓，因此可将这一能量区域内核素的截面看作常量，而通量在这一能量区域内的分布则认为符合1/E分布，这样根据式(4)即可计算超细群首群的散射源。得到超细群首群的散射源后，首群的中子通量即可通过1次单群固定源计算得到，而得到的中子通量又可用于下一群的散射源计算，依次进行这样的计算，即可得到整个超细群能量范围的精细能谱，根据式(6)可归并出某个共振群G的共振自屏截面。

(6)

固定源计算的准确与否直接影响到共振自屏截面的计算精度，本文通过耦合西安交通大学开发的模块化特征线法程序MOCHA[12]进行超细群的群内固定源计算。MOC利用数学方法将中子输运方程转化为沿某一角度某一根特征线上的方程，可同时处理空间角度变量和空间变量，实现对任意几何的处理。模块化特征线法主要是指特征线的生成技术，该方法以模块为单位产生特征线，保证相邻模块之间特征线能首尾相连。

2 数值结果

本文共计算了1个典型压水堆栅元问题、1个带有温度分布的燃料栅元问题、1个燃料区存在UO2和MOX燃料粘合的特殊栅元问题以及1个板状组件问题，使用的多群数据库为WLUP[13]发布的基于ENDF-B-Ⅶ.0评价库[14]制作的WIMS格式69群数据库，其中第15～27能群为共振能群，耦合特征线的超细群慢化方程求解方法(UFG-MOC)使用的截面为使用NJOY程序[15]制作的基于ENDF-B-Ⅶ.0的点截面数据库。超细群的能群宽度设置为0.000 25，不加说明的情况下，MOC计算参数为32个方位角，8个极角(高斯-勒让德求积组)，射线间距为0.012 5 cm。所采用的参考结果由上文提到的基于碰撞概率插值的超细群程序UFOP计算或蒙特卡罗程序MCNP5[16]统计得到。MCNP计算设置为投入300代粒子舍弃50代，每代投入1 000 000个粒子。

2.1 压水堆栅元问题

本文使用UFG-MOC计算了不同235U富集度和不同水铀比的UO2单栅元问题以及不同Pu含量的MOX单栅元问题，单栅元的几何尺寸取自JAERI[17]发布的轻水堆基准题，问题中不同的水铀比是以改变燃料区与栅元总体积比来体现的。基准结果由UFOP程序计算得到。表1、2列出了这些问题的详细描述。

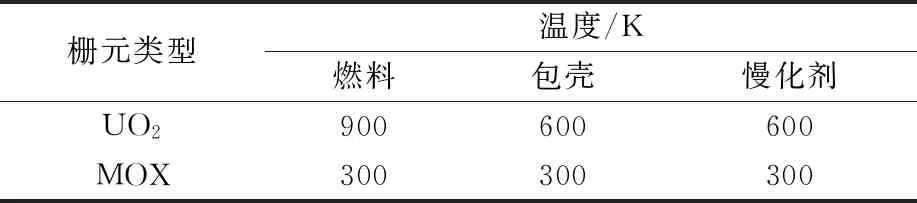
表1 不同类型栅元的温度分布Table 1 Temperature distribution of different pin cell types

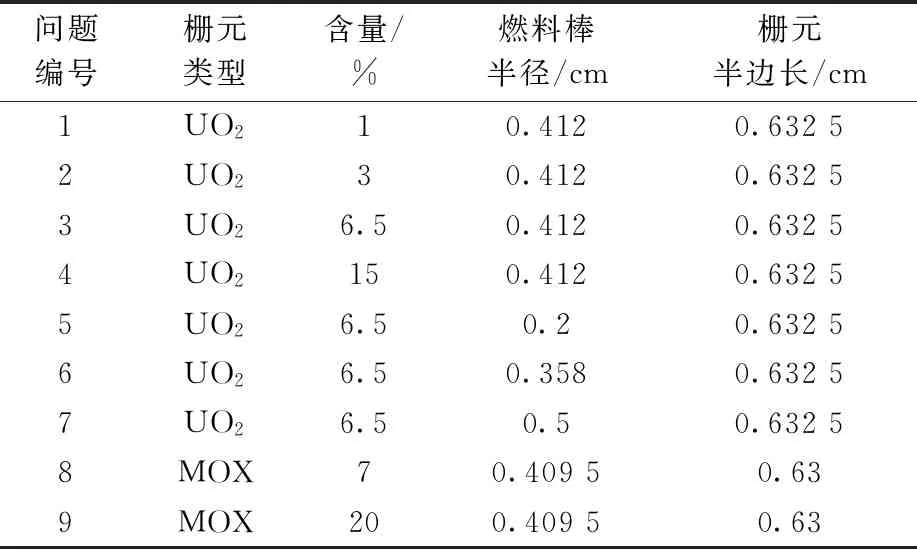
表2 栅元问题描述Table 2 Description of pin cell case

注：含量中UO2栅元为235U富集度，即质量分数；MOX栅元为Pu含量，即混合物中PuO2质量在PuO2和UO2质量之和的百分比

图1示出了9个子问题中235U、238U、239Pu的共振吸收截面计算结果和参考结果的相对误差，可看出，UFG-MOC中235U的相对误差不超过0.9%，238U的相对误差不超过1.3%，239Pu的相对误差不超过1.2%。

为避免输运计算方法不同等原因所导致的误差，分别使用UFG-MOC计算所得的共振截面和参考结果进行相同的MOC输运计算，表3列出不同问题计算的有效增殖因数keff的误差，最大误差为112.1 pcm。

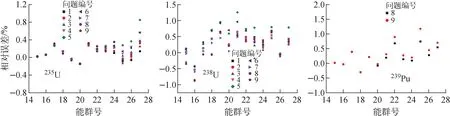
图1 不同问题的235U、238U、239Pu共振吸收截面相对误差Fig.1 Relative errors of 235U, 238U and 239Pu resonance absorption cross sections for different cases

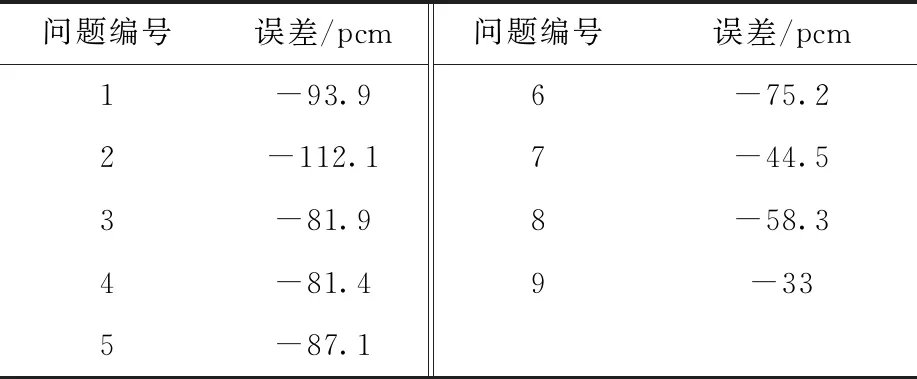
表3 不同问题中共振截面所引起的keff误差Table 3 Error of keff caused by resonance cross sections for different cases

2.2 带有温度分布的燃料栅元问题

在对燃料进行完整性评估[18]以及高保真计算[19]中，需对带有不等温分布的燃料棒进行精确的共振计算。传统计算中常采用空间相关的丹可夫方法(又称为SDDM方法)[17]进行计算，但存在一定误差，一些基于子群方法的改进也用于计算这类问题，但需对子群结构进行精细处理并且采用的半经验公式并不一定能反映真实问题[20]。对于基于碰撞概率插值的超细群程序如PEACO，当计算带有不等温分布的问题时，由于共振区增多，中子飞行首次碰撞概率的计算过于耗时，常采用均匀碰撞概率模型[21]，但这种计算存在理论缺陷，会引入一定误差[22]。

本文使用UFG-MOC对这类问题进行了计算，几何尺寸来自于JAERI发布的轻水堆基准题中的UO2栅元，燃料为富集度为6.5%的UO2燃料，包壳和慢化剂区域的温度为600 K。燃料区域从内到外被划分为等体积10环，每环的温度均不同，图2示出了燃料棒的空间离散情况。另外MOC计算时射线间距调整为0.005 cm。

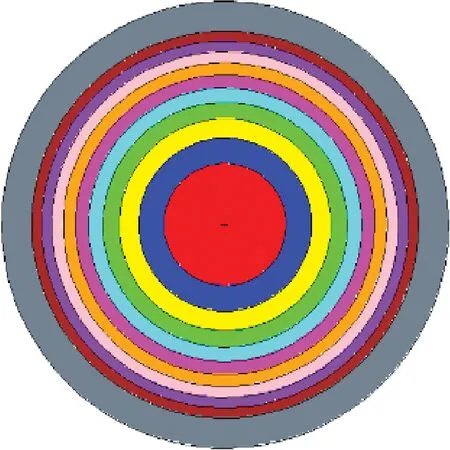
图2 燃料棒空间离散示意图Fig.2 Spatial discretization of fuel pin

表4列出了燃料棒温度分布。

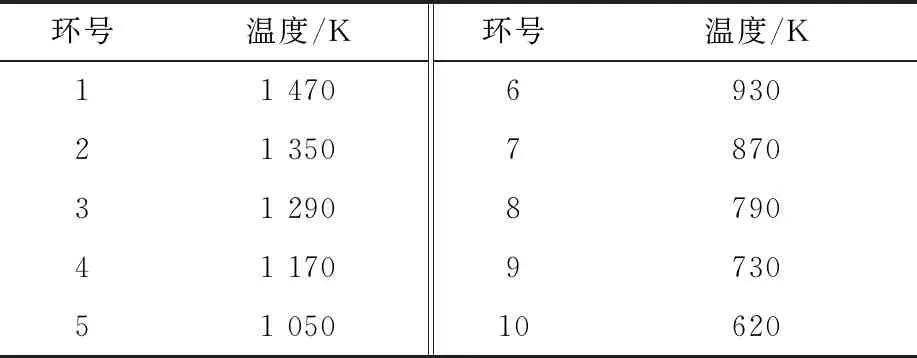
表4 燃料棒温度分布Table 4 Temperature profile of fuel pin

图3为UFG-MOC计算得到的第1、4、7、10环的238U吸收截面相对误差，参考结果来自于MCNP统计，最大相对误差不超过2%，大部分相对误差均在1%以内。分别使用UFG-MOC计算和MCNP统计得到的共振截面进行相同的MOC输运计算，所引起的keff误差为-68.5 pcm。

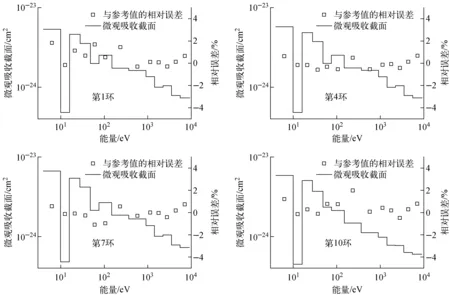
图3 第1、4、7、10环238U吸收截面相对误差Fig.3 Relative errors of group-wised 238U microscopic cross sections in ring 1, 4, 7 and 10

2.3 燃料内部存在不均匀性问题

随着核能技术的发展，未来燃料组件和栅元的设计将会更加复杂，因此设计了一个燃料棒内部存在两种材料的栅元问题。问题几何示于图4，1区为235U富集度为6.5%的UO2燃料，2区为Pu含量为20%的MOX燃料，温度均为300 K。对于这样的问题，传统的共振计算方法是无法计算的。

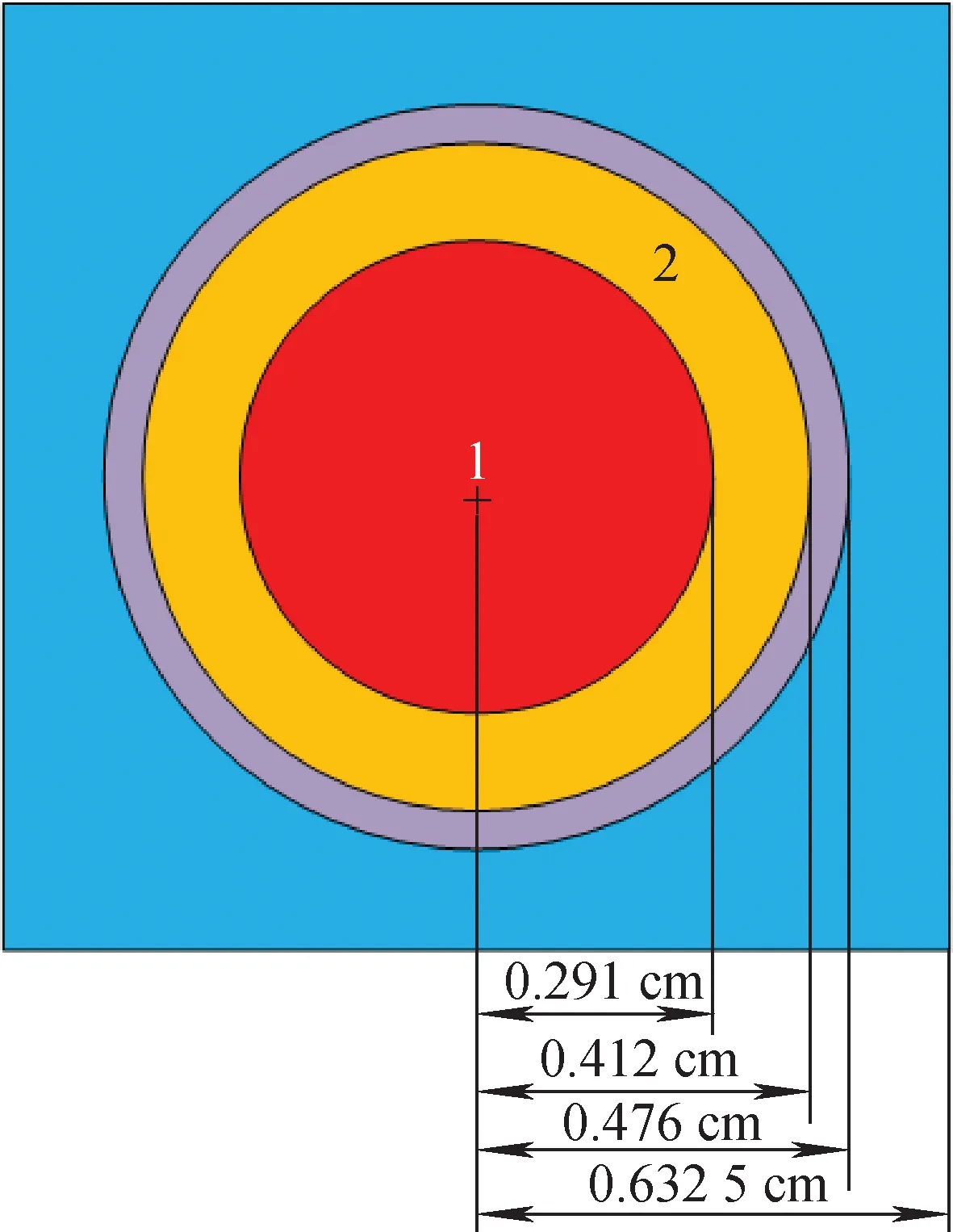
图4 本问题几何Fig.4 Geometry of this problem

图5示出了本问题中UO2和MOX燃料区域中部分主要共振核素的共振吸收截面与参考值的相对误差，参考值由UFOP程序计算得到。可看出，在UO2燃料区域，235U的共振吸收截面相对误差不超过0.4%，238U的共振吸收截面相对误差不超过1.3%，在MOX燃料区域，235U的共振吸收截面相对误差不超过0.4%，238U的共振吸收截面相对误差不超过1.3%，239Pu的共振吸收截面相对误差不超过0.7%。

另外，使用UFG-MOC计算所得的共振截面和参考值进行相同的MOC输运计算，所计算的keff的误差为30.3 pcm。

图6示出了3种不同情况下使用UFG-MOC所计算的4～9.877 eV归一化后的中子能谱可看到，由于钚核素在4.2 eV和7.8 eV附近的共振，MOX无限栅格的中子能谱在此处出现了相应的共振峰，而UO2-MOX问题中UO2燃料区域的中子能谱也出现了相同的现象，这说明UO2-MOX问题中的UO2燃料区域受到了来自MOX燃料区域的共振干涉，传统的共振计算方法如等价理论、子群方法均无法对这种现象进行准确计算，这体现了UFG-MOC在处理复杂能谱下的优势。

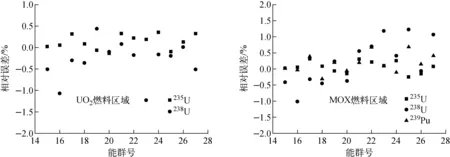
图5 UO2和MOX燃料区域主要共振核素的共振吸收截面相对误差Fig.5 Relative errors of resonance absorption cross sections for major resonance nuclides in UO2 and MOX fuel regions

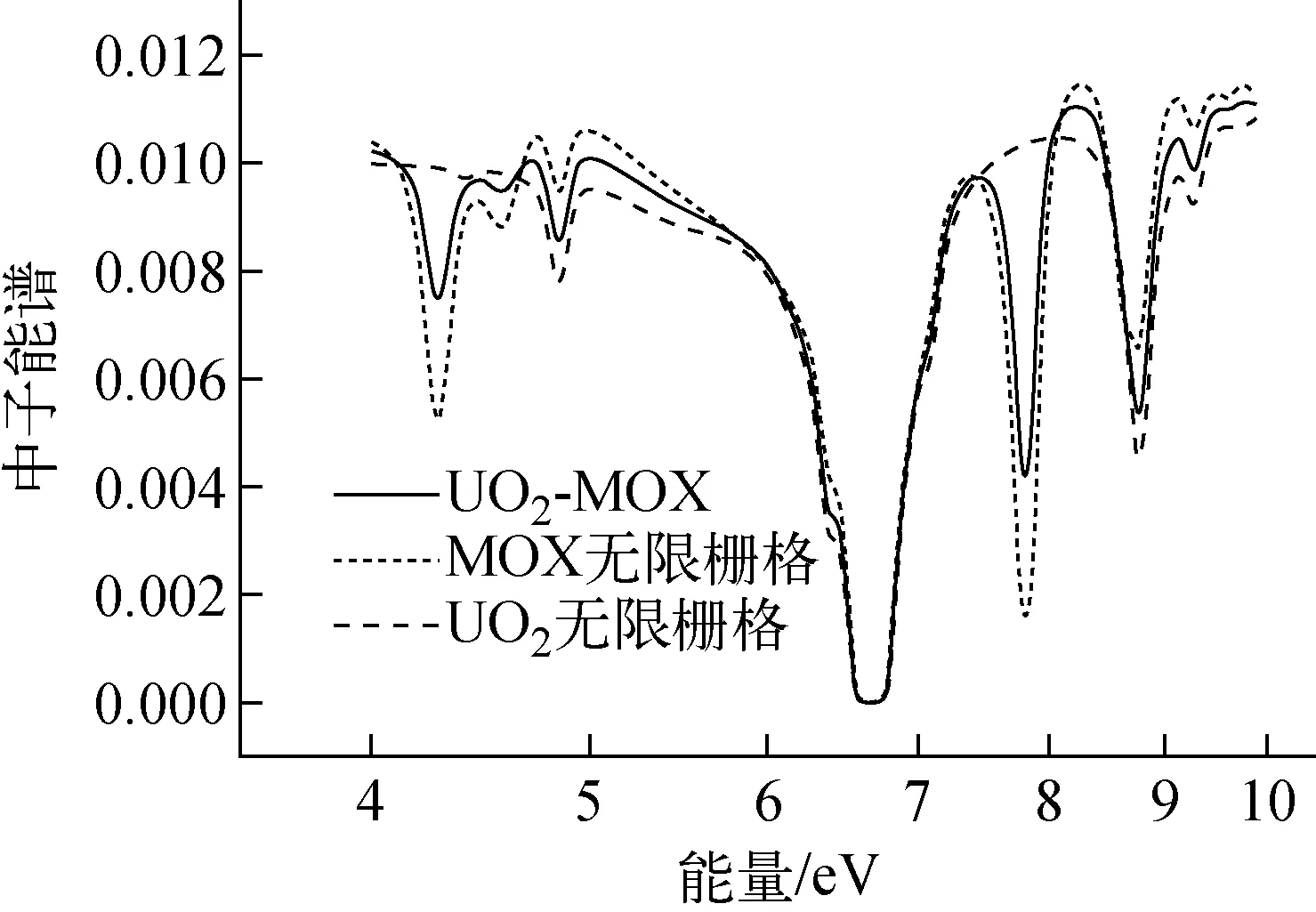
图6 UFG-MOC计算所得不同问题能谱Fig.6 Neutron spectra of different problems calculated by UFG-MOC

2.4 板状组件问题

本文所计算的板状组件由16块相同的单板栅元组装而成，为方便计算，对问题进行简化，问题中只包含燃料和慢化剂，几何示意图示于图7。燃料选取235U富集度为6.5%的UO2燃料，所有区域的温度均为300 K，采用的基准结果由MCNP5统计得到。

图8示出了图7中标注的1～4号燃料区使用UFG-MOC所计算的238U的共振吸收截面与MCNP参考结果的相对误差。可看出这4个区域的238U吸收截面的相对误差大多小于1%，最大不超过2%。与上述相同，将UFG-MOC计算的共振截面和MCNP统计的共振截面分别进行相同的MOC输运计算，计算得到共振截面所引起的keff的误差为-106.9 pcm。

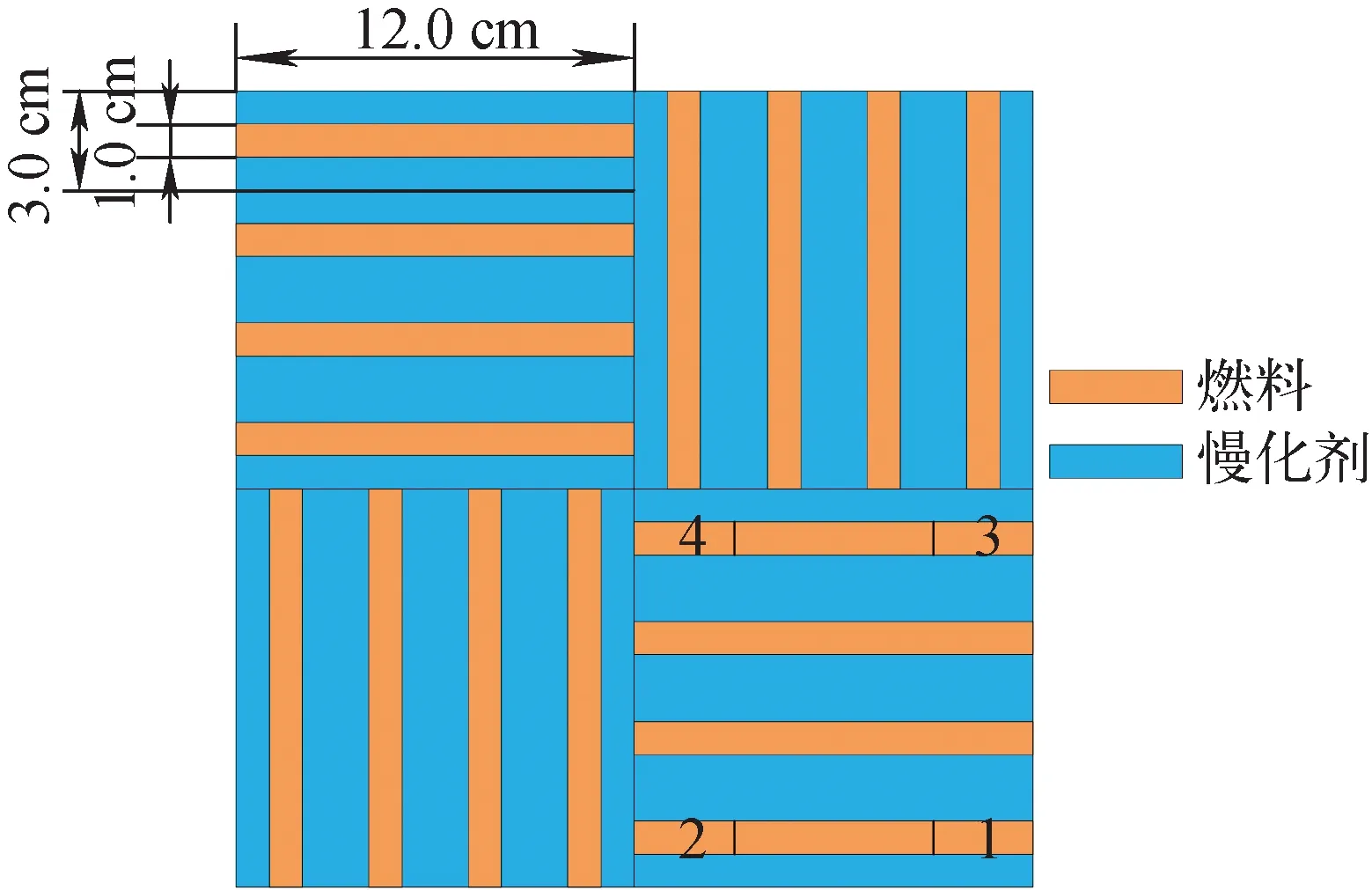
图7 板状燃料组件几何Fig.7 Slab fuel assembly geometry

等价理论在对板状燃料组件进行计算时通常会采用一维等效平板，但这种假设并未充分考虑板状组件中由于相互交错所引起的空间效应。使用UFG-MOC计算了具有相同燃料和慢化剂体积比的一维平板，表5列出了238U共振吸收截面的比较。可看到，单板栅元和交错并不显著的燃料1区，238U的共振吸收截面并不存在较大的差别，但在交错较为显著的燃料3区和4区，238U的共振吸收截面已出现了一定的差别，在交错最为显著的4区，238U吸收截面的误差已经超过了3%。这说明，在板状燃料组件中，燃料板的相互交错所引起的空间效应已给计算带来了不可忽略的影响。

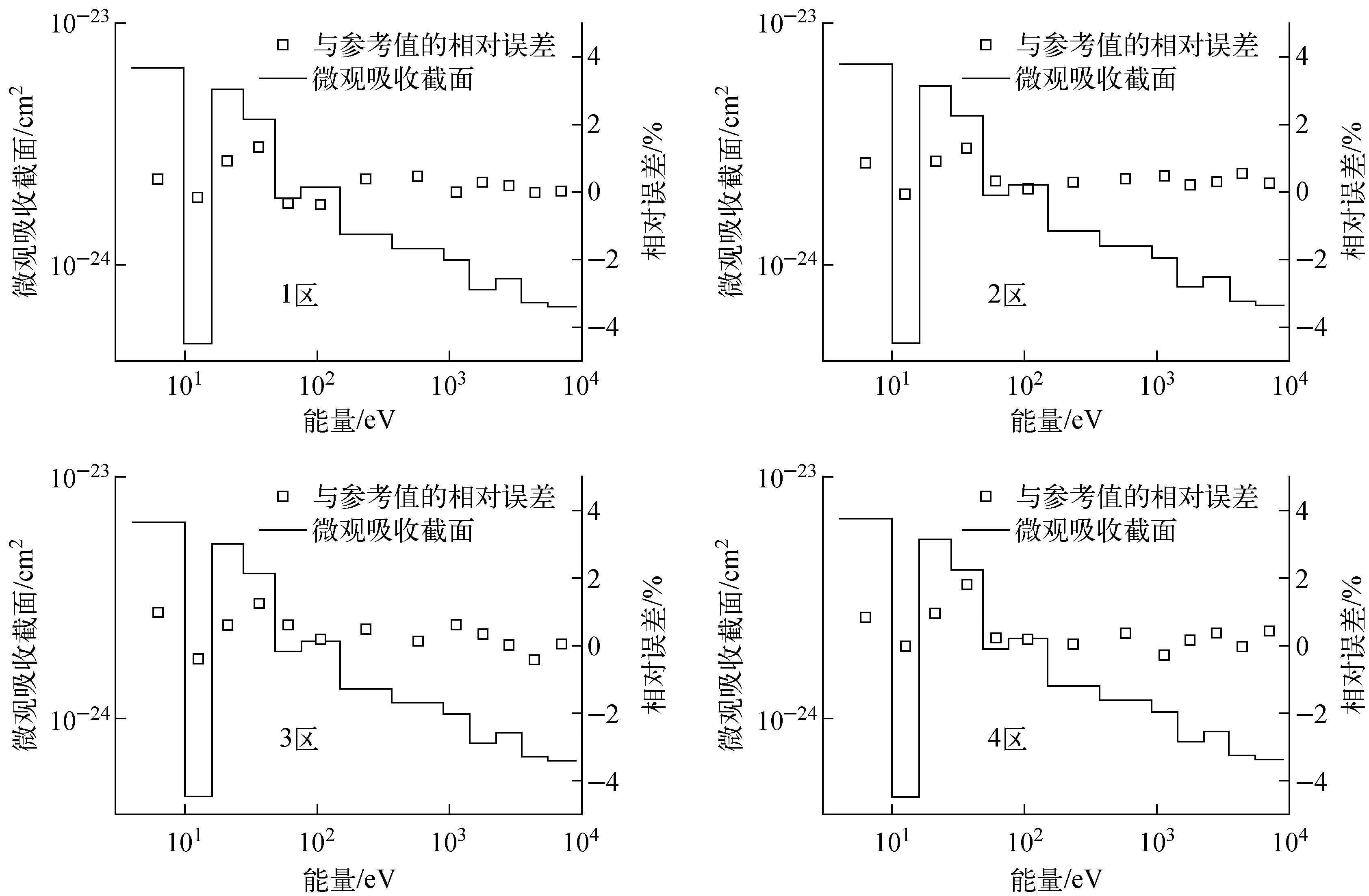
图8 1～4区中238U吸收截面相对误差Fig.8 Relative error of 238U microscopic absorption cross section in region 1-4

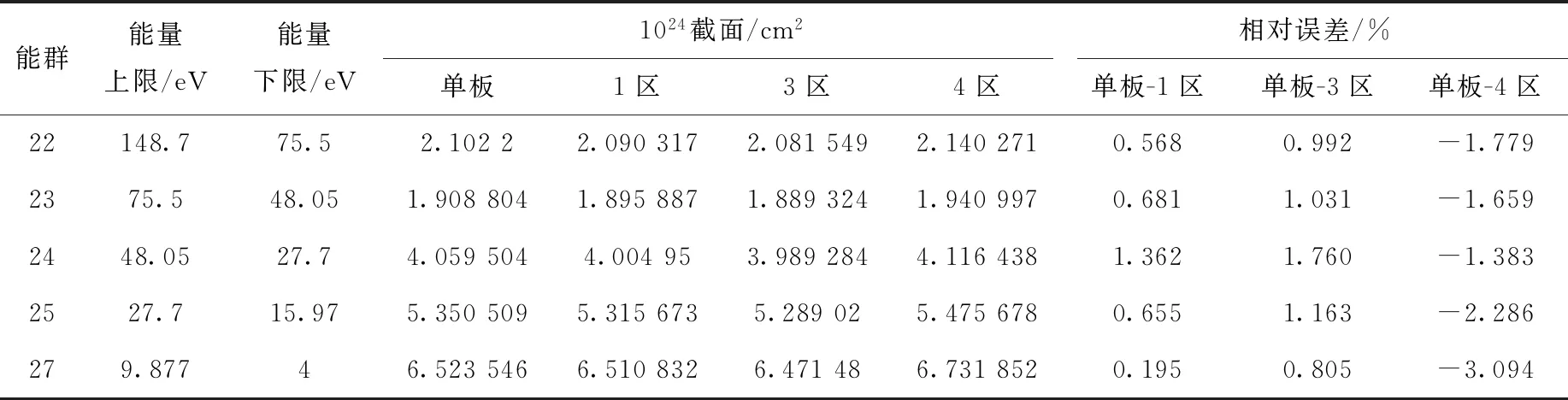
表5 238U共振吸收截面的比较Table 5 Comparison of 238U resonance absorption cross section

3 结论

本文提出了基于特征线计算的UFG-MOC，用于实现对于复杂几何、复杂能谱问题的精细共振计算。根据本方法对多种问题进行了计算，对共振自屏截面和其所引起的keff变化进行了对比，结果表明本方法可对多种复杂问题进行精确计算，为共振计算提供基准。与其他传统共振计算方法相比，UFG-MOC具有较高的计算精度，并且可直接有效解决不同核素间的共振干涉而不需要核素迭代或其他处理，与等价理论相比，UFG-MOC具有较强的几何处理能力，但同时应注意到，相比于等价理论和子群方法，UFG-MOC的计算效率不高，下一步可对提高计算效率展开研究。