基于层间模型知识迁移的深度堆叠最小二乘分类器

冯 伟 杭文龙 梁 爽 刘学军 王 辉

1(南京工业大学计算机科学与技术学院 南京 211816)2(南京邮电大学地理与生物信息学院 南京 210023)(fengwei@njtech.edu.cn)

最小二乘分类器(least square classifier,LSC)模型参数的解析解形式，使其通过留一交叉验证策略可以简便快速地确定最优模型参数(如平衡参数以及高斯核宽)，避免耗费大量计算成本进行参数寻优[1].因此，LSC模型被广泛应用于图像识别[2-3]、语音识别[4-5]、文本分类[6]等领域.然而，随着信息技术的发展，数据特征和结构趋于复杂化，例如遥感图像、医学图像等.这些数据往往需要专业领域人员根据应用场景设计特征提取器，将原始数据转化成分类器易于处理的数据特征形式.上述过程需要辅助大量的领域知识和专业经验，给传统的LSC模型在实际场景中的应用带来极大的挑战.

近年来，深度学习在理论与技术的突破性发展，表现出优于传统机器学习算法的性能[7].深度学习框架主要由多个非线性单元堆叠而成，其利用相邻前层的输出作为下一层的输入，经过多层特征提取后，自适应地从原始数据中抽象出有效的特征表示.深度学习方法由于其强大的特征学习能力受到学术界和工业界的广泛关注，目前已成功应用于计算机视觉[8-10]、自然语言处理[11-13]等领域.然而，主流的深度学习方法大多基于多层感知机，需要求解非凸优化问题，容易陷入局部最优值.且参数较多、模型训练时间过长[14-16].

针对这些问题，本文结合堆叠泛化理论以及迁移学习机制提出一种新的堆叠架构，在LSC模型的基础上提出了深度迁移最小二乘分类器(deep transfer least square classifier,DTLSC)，其具有2个特点：

1)基于堆叠泛化原理，利用LSC模型作为基本堆叠单元构建深度堆叠架构，避免了传统深度网络中需要求解非凸优化的问题，提升模型分类性能的同时提高了网络计算效率.具体地，DTLSC的第1层输入为原始数据.从第2层开始，每一层的输入由所有前层输出的随机投影与原始特征叠加而成.从而利用了前层输出递归地改变原始数据流形，有助于下一层分类器对数据进行分类.

2)利用迁移学习机制，自适应迁移所有前层网络的模型知识以辅助当前层网络的模型构建，以充分利用深度堆叠网络中各层之间的关联性，尽可能保持了层间模型的一致性，提升分类器泛化性能.此外，采用选择性迁移策略，通过最小化当前层训练集上的留一交叉验证误差，自适应地确定每个前层模型迁移知识的权重，避免因使用不相关模型知识导致的负迁移效应.

1 相关工作

Wolpert[17]首先提出堆叠泛化理论，通过将多个简单的函数或浅层分类器堆叠构成深度网络，以得到更加复杂的函数或者深层分类器，从而最终提升分类或预测的准确性.目前已经有较多关于深度堆叠架构的研究成果，根据堆叠单元不同，其方法大致可归纳为2类：1)通过堆叠多个多层感知机来构建深度网络，此类深度网络在相邻层间传递数据时通常不包含监督信息.目前应用较为广泛的有卷积神经网络(convolutional neural network,CNN)[18-19]、深度玻尔兹曼机(deep Boltzmann machines,DBM)[20-21]、深度自编码器(deep auto-encoder，DAE)[22-23]等.2)将多个简单的浅层分类器作为基本堆叠单元构建深度网络，该类深度网络通常利用前层输出以及原始输入特征构成当前层的输入.可以看出:此类深度网络在层间传递数据过程中利用了监督信息，提高了模型的分类性能.此外，由于每层只需使用一个简单的分类器，避免了由于求解非凸优化问题而容易陷入局部最优的问题.另外，通过利用前层的预测值递归改变原始数据流形结构，使得不同类别的数据样本更加可分，有助于提升整个深层架构的分类性能.Vinyals等人[24]提出了一种随机递归线性支持向量机(random recursive support vector machine，R2SVM)，将线性支持向量机(support vector machine，SVM)作为基本堆叠单元，同时引入随机投影作为核心堆叠元素;Yu等人[25]结合极限学习机与堆叠泛化理论，提出了极限学习机深度网络结构(deep representations learning via extreme learning machine，DrELM);Wang等人[26]提出了深度迁移叠加核最小二乘支持向量机(deep transfer additive kernel least square support vector machine,DTA-LSSVM)，所提深度网络以叠加核最小二乘支持向量机(additive kernel least square support vector machine,AK-LSSVM)作为基本堆叠单元，将上一层输出作为一个附加特征对原始特征扩维作为当前层的输入，并且在相邻层之间进行知识迁移以提升模型的泛化性能.然而，目前这类深度堆叠架构大部分均未充分考虑到深度堆叠网络中各层之间的关联性，模型的泛化性能有待进一步改善.

本文所提DTLSC算法利用LSC作为基本堆叠单元构建深度堆叠网络，每层输入均由所有前层输出的随机投影结果与原始输入特征叠加而成，同时引入选择性迁移学习机制，对所有前层的模型知识进行自适应迁移来辅助当前层模型的构建.值得注意的是，在深度堆叠网络构建过程中，相比于DTA-LSSVM仅迁移前一层的模型知识，DTLSC算法利用了文献[24]中的数据生成方式，递归地改变原始数据流形，增加了数据的可分性；此外，DTLSC算法考虑了所有前层之间的关联性，采用自适应迁移学习技术，能合理有效地利用所有前层的模型知识，进一步提升了模型的泛化性能[26].

2 问题定义

Table 1 Parameters Description表1 参数描述

本文介绍经典的LSC模型，然后给出本文提出的DTLSC算法.

3 最小二乘分类器

基于等式约束，Suykens等人在文献[27]中给出了LSC模型：

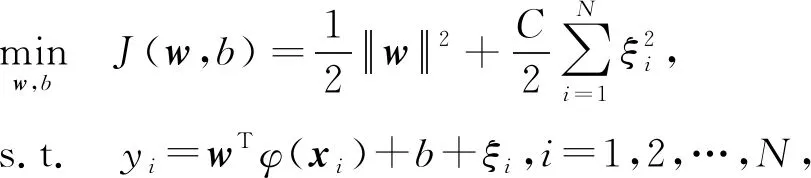
(1)

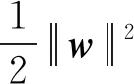
LSC模型的优化可以归结为线性方程组的求解问题，由于使用了等式约束使其较易得到方程的解析解形式.然而，传统LSC模型在有限的样本和计算单元的情况下对复杂函数的表示能力有限，处理复杂的分类问题时存在局限性.

4 深度迁移最小二乘分类器

本文基于堆叠泛化理论和迁移学习机制，提出一种深度迁移最小二乘分类器DTLSC，该算法充分利用了深度堆叠架构以及迁移学习的优势来提高LSC模型的学习与泛化性能，以提升传统LSC在处理复杂的数据特征时的分类效果.

4.1 基本框架

DTLSC算法总体框架如图1所示:

Fig.1 The overall framework of DTLSC图1 DTLSC的整体框架

具体地，DTLSC算法第1层基本单元为传统LSC，其输入为原始数据X.从第2层开始，每一层的输入由所有前层输出的随机投影与原始输入特征叠加而成.利用前层输出的随机投影可以改变原始数据的流形结构[24]，使得数据更具可分性，从而提升了分类器的分类性能.此外，从第2层开始，每层基本模块为迁移LSC.具体地，采用迁移学习策略，自适应地学习前层模型知识来辅助当前层的分类模型构建.

Fig.2 Composition of the l th layer input图2 第l层输入数据的构成

(2)

其中,pl,j表示第l层用于投影第j层输出的投影矩阵.

4.2 自适应深度迁移

深度堆叠网络中各层之间存在一定的关联性[26]，为尽可能保持层间模型的一致性，DTLSC算法在深度堆叠架构中引入迁移学习机制，利用前层的相关模型知识辅助当前层的模型构建，以进一步提升模型的泛化性能.具体地，以构建第l层模型为例，下面将介绍自适应迁移前l-1层模型的详细过程.首先，我们引入模型知识迁移权重βj,l，j=1,2,…,l-1，用于表示网络层间知识迁移的程度，βj,l反映了第j层与当前第l层模型知识之间的相关程度.给出DTLSC算法的目标函数：

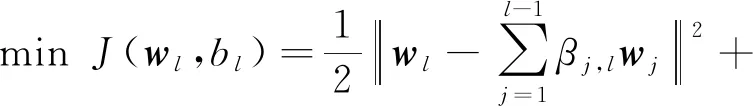
(3)

其中,Cl为当前层权衡函数复杂度和分类误差的平衡参数，ξi,l为第l层第i个训练样本的分类误差.可以看出，当β1,l=β2,l…=βl-1,l=0时，目标函数退化为传统LSC模型.

从式(3)看出，由于引入反映深度网络结构层间迁移程度的模型参数βj,l，j=1,2,…,l-1，DTLSC算法能够缓解利用不相关的前层模型知识而导致的负迁移效应，保证了模型的泛化性能.

4.3 算法求解

式(3)的拉格朗日形式：

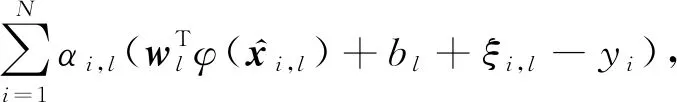
(4)

(5)

(6)

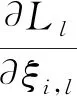
(7)

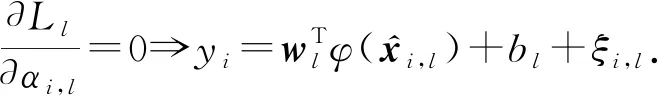
(8)

将式(5)～(7)代入式(8)，可得:

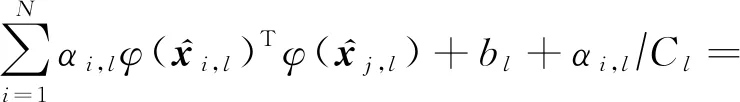
(9)

将式(9)写成矩阵形式，可得:

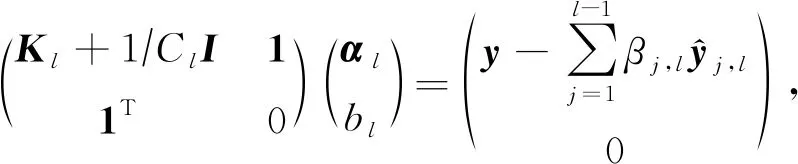
(10)

采用Ml表示式(10)等号左边第1个矩阵，即：

(11)

则可以得到当前层的模型参数，即:

(12)

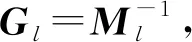
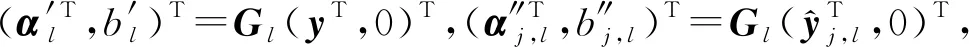
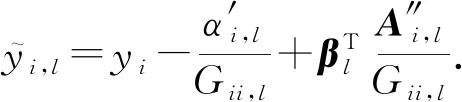
(13)

证明.令α(-i),l和b(-i),l表示第l层留一交叉验证中第i次迭代得到的模型参数.在第1次迭代时，第1个样本被取出作为测试集，可得:

(14)

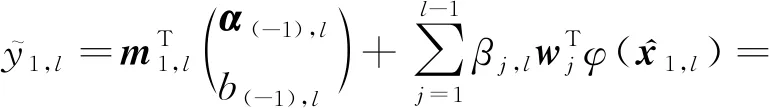
(15)

结合式(10)和式(11)可知:

因此：

(16)

由式(10)可得:

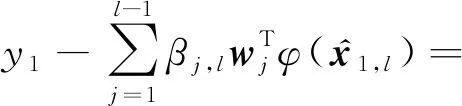
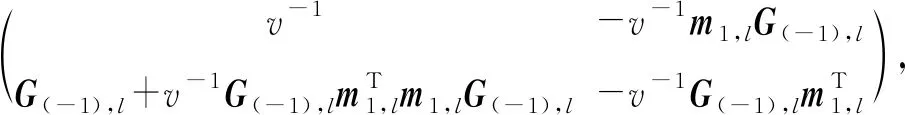
(17)

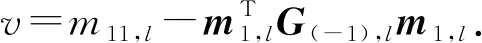
(18)

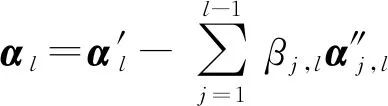
(19)

证毕.

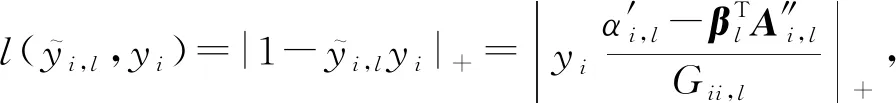
(20)

其中,|x|+=max(0,x).

则最优化βl可表示为目标函数：

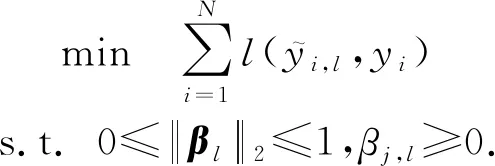
(21)

式(21)可通过梯度下降法求解，伪代码如算法1所示.

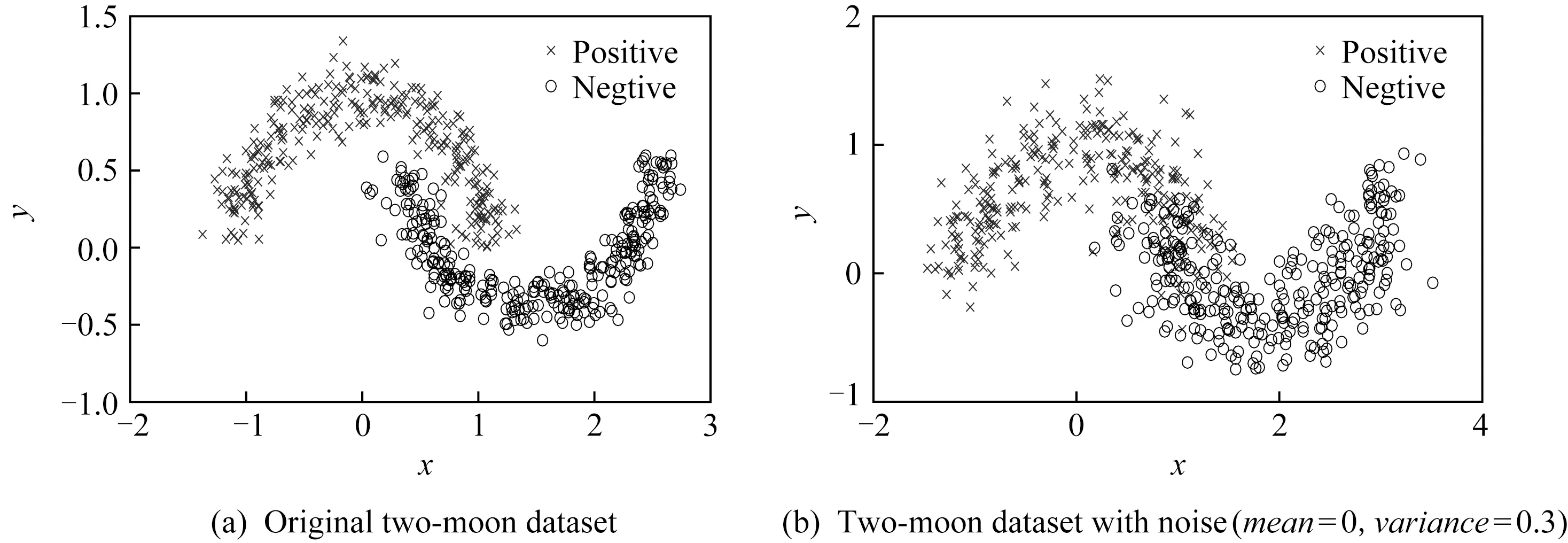
Fig.3 Artificial dataset图3 人造数据集

算法1.梯度下降优化算法.

输出：βl.

初始化：βl=0，当前迭代值t=1；

Repeat

end if

Step5.βj,l←max(βj,l,0),∀j=1,2,…,l-1；

Step6.t←t+1；

Until convergence

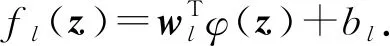
4.4 时间复杂度分析

DTLSC算法使用留一交叉验证策略快速地进行模型参数选择，其仅需要较少的计算时间便可以获得最优参数.在深度网络建立过程中，第1层进行LSC模型构建的时间复杂度为O(N3).从第2层开始，每个模块的时间复杂度主要分为2个部分:1)求矩阵Ml的逆运算，相应的时间复杂度为O(N3);2)用梯度下降法迭代求出迁移权重βl，相应的时间复杂度为O((L-1)N).因此，DTLSC算法的整个时间复杂度为O(LN3+(L-1)2N).

5 实验与分析

本节将对所提DTLSC算法在人造数据集和真实数据集上的分类效果进行实验验证与分析.

5.1 实验数据集

1)人造数据集.本文将验证在不同噪声下算法的分类性能.首先构造正、负类各300个样本的双月数据集,图3(a)所示.随后分别对双月数据集施加不同的高斯噪声(均值为0，方差分别为0.1,0.3,0.5,0.8,1).图3(b)中展示的是施加了均值为0、方差为0.3噪声的双月数据集.

2)真实数据集.为进一步验证DTLSC算法的分类性能，本文在10个UCI数据集上进行了实验验证，具体描述如表2所示:

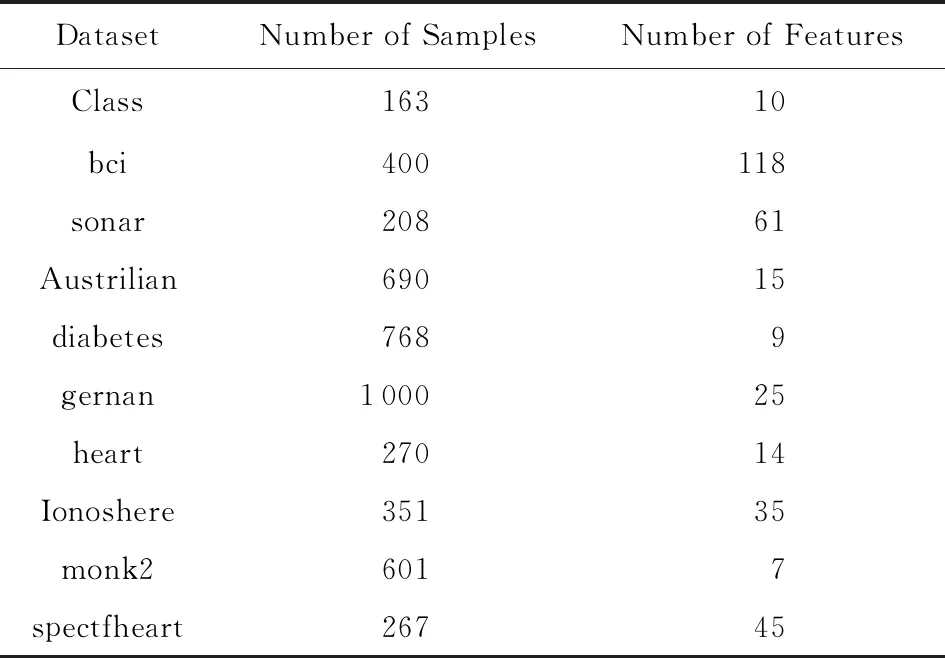
Table 2 Description of UCI Datasets表2 UCI数据集描述

5.2 实验设置

本文采用5种对比算法：

1)经典最小二乘分类器(LSC)[27]；

2)随机递归层叠LSC(RRLSC)[24]；

3)深层迁移叠加核LSC(DTA-LSC)[26]；

4)本文所提DTLSC算法；

5)仅迁移前一层模型知识的DTLSC算法(DTLSC-S).

在上述对比算法中，本文将R2SVM算法的基本单元替换成LSC模型；此外，将DTA-LSSVM算法的基本单元(AK-LSSVM)替换成LSC模型.所有算法均采用线性核和RBF核，参数设置如表3所示：

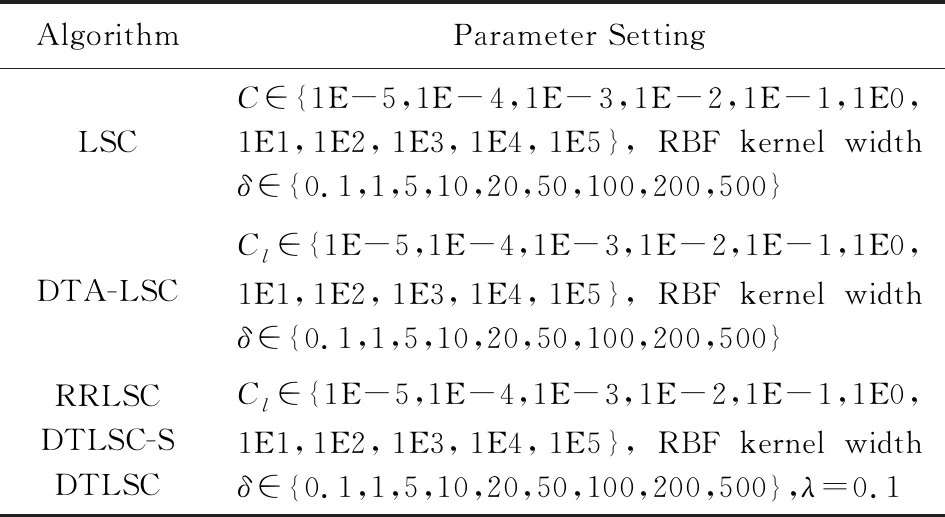
Table 3 Parameter Setup表3 实验参数设置

对于人造数据集以及真实数据集，分别随机抽取20%和30%的样本用于训练，剩下的样本用于测试，数据均统一进行归一化处理.在训练过程中采用五折交叉验证方法确定最优参数Cl和δ.同时采用分类精度评估各算法的性能，具体表示为

(22)

其中，Dte表示测试数据集，yi表示zi的真实标签，sgn(f(zi))为zi的预测标签.所有算法均执行10次，最后计算出各自的均值与方差.

本文实验硬件平台为Windows 64位Intel Core i5，内存为8 GB.编程环境为MATLAB 2014b.

5.3 实验结果

5.3.1 人造数据集实验结果

图4(a)(b)分别展示了设置20%样本用于训练时各对比算法采用RBF核及线性核的分类精度.图4(c)(d)分别展示了设置30%样本用于训练时各对比算法采用RBF核及线性核的分类精度.根据图4可以得到结论：4种深度堆叠算法，即RRLSC，DTA-LSC，DTLSC-S，DTLSC较浅层学习算法LSC可以获得更好的分类准确率.这主要是因为基于深度堆叠架构的分类器模型能够改变数据的流形结构，模型的分类性能得到提升.在一般情况下，对比无迁移的深度堆叠架构RRLSC，深度迁移堆叠架构DTA-LSC，DTLSC-S能获得更高的分类精度，但却都要逊于DTLSC算法.其原因主要是 DTA-LSC和 DTLSC-S仅仅利用了前一层模型的知识来辅助当前层分类器模型的构建，并未考虑到深度堆叠网络中其他前层之间的关联性.DTLSC算法通过自适应迁移所有前层模型的有用知识可以改善上述问题，增强了模型的泛化性能.可以看出，本文所提DTLSC算法算法在人造数据集上的分类性能优于其他对比算法.此外，由于DTLSC算法能够利用留一交叉验证法快速、自适应地决策各前层模型知识的迁移权重，可以避免因利用不相关模型知识导致的负迁移效应，具备一定的实用价值.

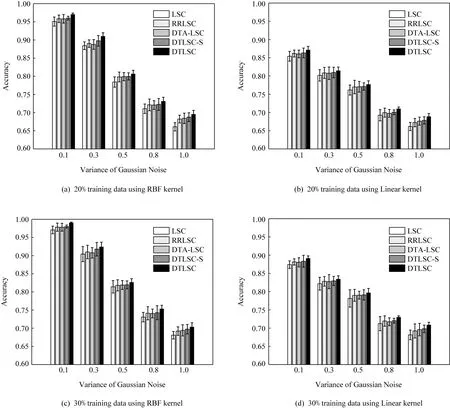
Fig.4 Results of different algorithms on the two-moon dataset图4 不同算法在双月数据集上的实验结果

5.3.2 真实数据集实验结果

表4～7分别给出了各个对比算法在UCI数据集上的分类精度.其中，表4～5为仅有20%训练数据时，分别采用线性核以及RBF核的分类结果；表6～7为有30%训练数据时，采用线性核以及RBF核的分类结果.从各算法的分类结果中，可得到3个结论：

Table 4 Accuracy of Comparison Algorithms on Ten UCI Datasets (RBF Kernel,20% Training Data)表4 对比算法在10个UCI数据集上的精确度结果(RBF核,20%训练数据)

Note:The values in boldface represent the highestclassification accuracy.

Table 5 Accuracy of Comparison Algorithms on Ten UCI Datasets (Linear Kernel,20% Training Data)表5 对比算法在10个UCI数据集上的精确度结果(线性核,20%训练数据)

Note:The values in boldface represent the highestclassification accuracy.

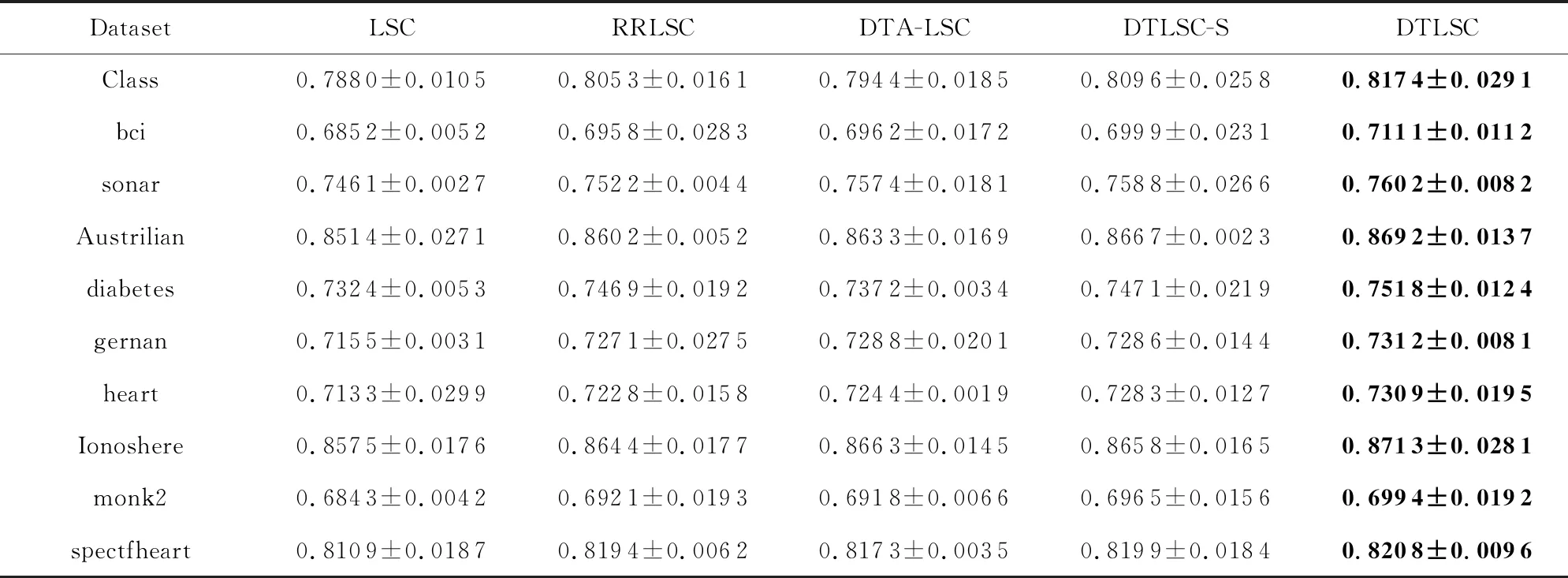
Table 6 Accuracy of Comparison Algorithms on Ten UCI datasets (RBF Kernel,30% Training Data)表6 对比算法在10个UCI数据集上的精确度结果(RBF核,30%训练数据)

Note:The values in boldface represent the highestclassification accuracy.

Table 7 Accuracy of Comparison Algorithms on Ten UCI Datasets (Linear Kernel,30% Training Data)表7 对比算法在10个UCI数据集上的精确度结果(线性核,30%训练数据)

Note:The values in boldface represent the highestclassification accuracy.

1)RRLSC的分类精度优于LSC.这主要是由于RRLSC利用前层输出的随机投影改变了数据的流形结构，使得不同类别的数据相互分离，增加了数据可分性.

2)DTA-LSC以及DTLSC-S算法的分类精度优于RRLSC.这主要是由于DTA-LSC，DTLSC-S都考虑了相邻层的关联性，利用相邻层的模型知识以辅助当前层模型的构建，提升了模型的泛化性能.

3)本文所提算法DTLSC的分类精度优于DTLSC-S以及DTA-LSC算法.这主要是由于DTLSC-S，DTA-LSC仅利用了相邻层间的模型知识，虽然具备一定的迁移效果，却忽略了其他前层蕴含的有用知识.DTLSC算法能够选择性地迁移所有前层模型知识，最大化利用深度堆叠网络中各层之间的关联性，进一步增强了模型的泛化性能，故其分类效果得到提升.

综上，通过在人造数据集以及真实数据集上的实验与分析，验证了DTLSC算法的可行性与有效性.

6 结 论

本文基于堆叠泛化理论与迁移学习机制，提出了深度迁移最小二乘分类器DTLSC.所提算法既利用了前层输出的随机投影改变了输入数据间的流形结构，增加了数据间的可分性，同时通过自适应迁移所有前层的模型知识来辅助当前层模型的构建，能够最大化利用深度堆叠网络中各层之间的关联性，尽可能保持层间模型的一致性，增强了分类模型的泛化性能.此外，基于留一交叉验证策略，能够快速决策网络中所有前层模型知识的迁移权重，避免了利用不相关模型知识导致的负迁移效应，提高了模型的可靠性.在人造数据集和真实数据集上的实验结果均验证了本文所提DTLSC算法的有效性.

尽管DTLSC算法表现出良好的分类性能，但仍存在部分需要进一步研究的问题.例如，如何将hinge loss 函数的优异学习能力与本文所提快速模型知识迁移权重求解方法相结合；如何将DTLSC算法拓展到多分类任务中以及其他的学习系统中(如模糊系统)等均是我们未来研究工作的重点内容.