基于模糊Black-Scholes模型的螺纹钢期权定价

李明昕, 唐 俊, 白 云, 马行达

(内蒙古科技大学 理学院,内蒙古 包头 014010)

0 引言

钢铁价格与下游相关行业产品价格之间存在着平衡关系。在短时间内受各种因素的影响，使得钢铁价格上下波动出现产生偏离平衡值的现象，但从长期来看，终将达到平衡状态。本文通过对螺纹钢价格的研究，在现有螺纹钢实物期权定价模型的基础上，采用模糊数学方法优化现有螺纹钢实物期权定价模型，探究现有模型的不足之处，减少或者避免风险对螺纹钢实物期权价格的影响[1]。在此基础上进一步探讨螺纹钢实物衍生品的风险来源、成因和传导机制，提出了相应的风险管理措施，具体步骤如下：

第一步：经典的布莱克-斯科尔斯实物期权定价模型(Black-Scholes实物期权定价模型，以下简称B-S模型)存在着一定的局限性，本文将通过一系列的优化过程，将其转变为模糊B-S实物期权定价模型[2,3]。

第二步：隶属度α的确定是运用和建立模糊B-S实物期权定价模型的核心。本文将数据进行判断矩阵变换、尺度转换以及综合评定结果计算等过程，确定模糊B-S实物期权定价模型所适用的隶属度α[4～6]。采用模糊数学方法来确定收益率和风险度量值的优点是可以控制收益率和风险所在的区间，克服由于经典B-S模型采用历史数据进行收益率和风险度量值拟合单个数据而带来的不精确性，使得模型实际应用更加合理且具有可操作性。

第三步：利用VaR在险价值方法(Value at Risk)，对融资风险进行量化，为实体金融风险的管理提供理论依据[7,8]。

第四步：利用模糊B-S实物期权定价模型进行实例分析和计算。

1 模糊B-S期权定价理论

1.1 B-S期权定价模型

经典B-S期权定价模型为[2]：

C=SN(d1)-Xe-rTN(d2)

(1)

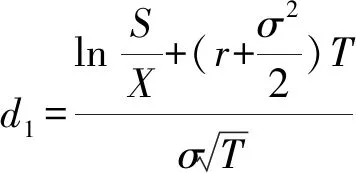
(2)

表1 符号表

在该B-S期权定价模型中，无风险利率通常以复利年息进行计算，期权剩余存续时间用分数计算，即期权剩余存续天数与365天的比值。

1.2 三角模糊数

首先，我们给出模糊数的定义[9]：

设在数域U上给定了映射：

(3)

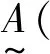
定义：假设A∈F(u)(模糊幂集)[9]

(4)

(5)

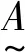
图1 隶属函数坐标

(6)

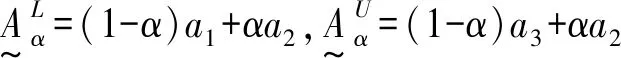
(7)

1.3 模糊B-S期权定价模型

模型假设[10]：(1)无风险利率不随时间的变化而改变；(2)标的资产价格(即实物期权项目的未来现金流现值)的波动服从布朗运动，其收益率服从对数分布；(3)风险投资没有分红；(4)贷款利息忽略不计。

对经典B-S实物期权定价模型中的波动率σ、无风险利率r以及标的资产价格S这三个变量进行模糊化后，可以得到以下结果：

(8)

其中，每个变量由三个数构成，三个数表示变量估计值的最小值、最可能值和最大值。

我们将上述三个自变量带入经典B-S期权定价模型，可以进一步推导出模糊B-S实物期权定价模型的公式[2]:

(9)

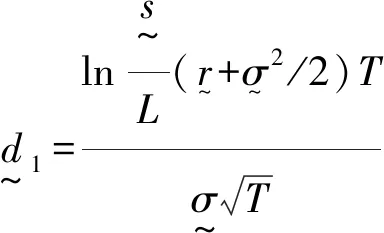
(10)

引入α-水平集的定义：

(11)

根据三角模糊数的四则运算规则，我们将模糊B-S实物期权定价模型转换为以下形式:

(12)

(13)

(14)

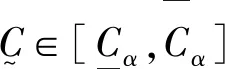
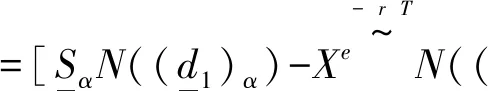
(15)

其中:

(16)

2 VaR模型

2.1 VaR在险价值度量模型

VaR方法(Value at Risk)，其意义是在一定的的显著水平下，对某既定的目标期间内，不利的市场变动可能导致资产价值的预期最大亏损的一种估计[4,8]。可以表示为:

P(ΔV<-VaR)=1-p

(17)

其中，ΔV表示投资组合价值的收益；1-p为尾部水平。

2.2 VaR的计算

假定某种股票的现价为S，年波动率为σ，年收益率r服从标准正态分布，即r～N(0,σ)，p=0.95。计算接下来一段时间内可能出现的最大亏损。假定：

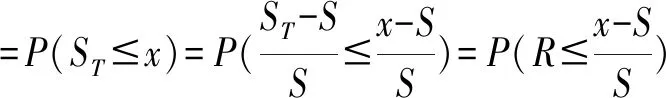
(18)

⟹F-1(1-p)=x=S+SσN-1(1-p)

(19)

所以：VaR=S-F-1(1-p)=S-S-SσN-1(1-p)

=-SσN-1(1-p)

(20)

其中，N(·)为标准正态分布；N-1(·)为标准正态分布的逆分布；p为置信水平，一般取p=0.95。

根据上述的VaR计算度量模型，本文通过某企业螺纹钢的产品数据，即螺纹钢实物期权的预期现金流现值和风险波动率，利用VaR计算度量模型，计算这一实物期权在给定置信水平下的损失大小，由此来判断此螺纹钢实物期权的风险大小，从而制定风险管理决策。

3 模糊B-S实物期权定价模型实例分析

3.1 隶属度α的确定

设定螺纹钢风险等级量化向B=(0.0974,0.2417,0.3353,0.2731,0.0628)[4,7,8]，并构建风险量化标准V=(0.9、0.8、0.7、0.6、0.5)，V中各个数字表示的意义见表2:

表2 风险评价等级量化表

即可获得最终的风险量化结果：

(21)

根据有关钢铁行业的判断矩阵和风险综合评价矩阵[4,7]，通过尺度变换、一致性检验和综合评价结果计算等一系列的工作，我们得出对于钢铁行业风险项目的可控程度为0.7110。本文将风险量化的最终结果作为模糊B-S实物期权定价模型中的隶属度，即α=0.7110。为了便于后续的计算，本文保留两位有效数字，即α=0.71。

3.2 模糊B-S实物期权定价模型的应用

本文以某钢铁(集团)有限责任公司螺纹钢投资计划书为数据来源，通过模糊B-S实物期权定价模型进行案例分析。

假设在未来一段时间内，该公司的新开项目的年产量为150万吨，原材料价格为461.5元/吨，生产综合加工成本为291元/吨，税率25%，其他成本为7261万元。则可以得到项目投资计划表：

表3 项目投资计划表

假设该项目分为两期，第一期为5年的基建期，从2009年1月1日开始，到2013年12月31日结束，项目总共投资107003.2万元，没有盈利收入；第二期为营业期，从2014年1月1日开始，到2019年12月31日结束，持续5年，每年的税后现金流量为13741万元，规定此项目的必要报酬率为10%，五年期内的无风险利率(五年期国债贴现率)恒定不变，为4.17%，为便于后续计算，我们暂且按4%处理。那么营业期5年项目的现值为:

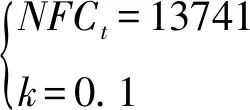
(22)

则S=32343.29。由于项目总投资金额为107003.2万元，假设项目在建设期期初投资一半，另一半则在建设期期末投资。则项目总投资金额的现值为:

(23)

则X=97476.02。由于营业期期初的投资额为53501.6，则可以得到营业期的净现值为:

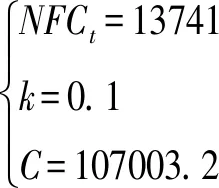
(24)

从上面的计算结果可以看出，此项目在营业期5年内的NPV为负的876.99，显然是不可取的。

据国内股票期货市场经验行情可知，股票市场的价格平均波动率约为30%，定义该钢铁投资项目的资产价格波动率大约为33%，即σ=0.33。

根据以上数据，此投资项目期权的主要参数：

表4 模糊B-S实物期权定价模型参数表

把经典B-S实物期权定价模型的三个变量：无风险利率、波动率、标的资产价格进行模糊化处理后，得到结果如下:

r=(0.036,0.04,0.044),σ=(0.30,0.33,0.36),S=(29108.96,32343.29,35577.62)

根据公式(6)，运用三角模糊数的运算规则，在α=0.71的情况下对以上3个参数进行模糊化运算，可以得到：

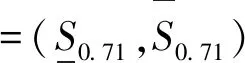
=(s1(1-α)+αs2,s3(1-α)+αs2)

=(31405.33,33281.25)

(25)

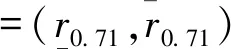
=(r1(1-α)+αr2,r3(1-α)+αr2)

=(0.03884,0.04116)

(26)

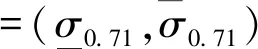
=(σ1(1-α)+ασ2,σ3(1-α)+ασ2)

=(0.32043,0.33957)

(27)

我们带入公式(16)可以得到：

=-0.2150

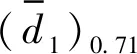
=-0.0854

(28)

由模糊B-S期权定价模型公式(15)可以得到：

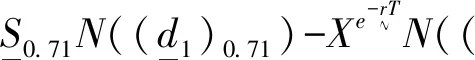
(29)

此项目的净现值NPV为负的876.99，故可以得到此项目的期权实际价值为(6502.97-876.99，6727.15-876.99)，即(5625.98，5850.16)。

3.3 VaR在险价值方法应用

据某钢铁(集团)有限责任公司螺纹钢投资计划书数据我们可以得到以下计算：

表5 VaR值计算参数表

根据公式(20)我们可以计算出此螺纹钢实物期权的在险价值为：

VaR=-SσN-1(1-p)

=-32343.29×0.33×N-1(0.05)

=17556

(30)

运用模糊B-S实物期权定价模型，可以得到此螺纹钢项目在风险可控度为0.71时其价值为(5625.98，5850.16)万元，短期利润额即可超过11%，投资可行性较高。根据风险测算结果可知，此项目在5%的显著水平下的在险价值为17556万元，此项目总投资为107003.2万元，其风险大小对比多种大型实物期权风险投资而言，风险基本可控，此项计算为投资者进一步优化投资决策提供了理论依据。

4 结论

根据本文研究结果可以知道，模糊B-S实物期权定价模型在实际问题中，得到的是风险投资项目期权价格的区间范围，与经典B-S期权定价模型相比，模糊B-S实物期权定价模型引入了项目综合评定过程，分析了风险项目可能不完全实现的问题，考虑了风险项目不同的外部风险情况，这使得钢铁项目的投资者在投资前有一个价格参考区间，而非一个精确值[9～16]。如图2所示，在不同的外部风险情况下，所得到的项目隶属度也不同，从而使得风险项目的期权价格区间也不同。从图2可以看出，风险项目的风险可控度越高，即模糊B-S实物期权定价模型的隶属度越大，那么风险项目期权价格区间也越精确。

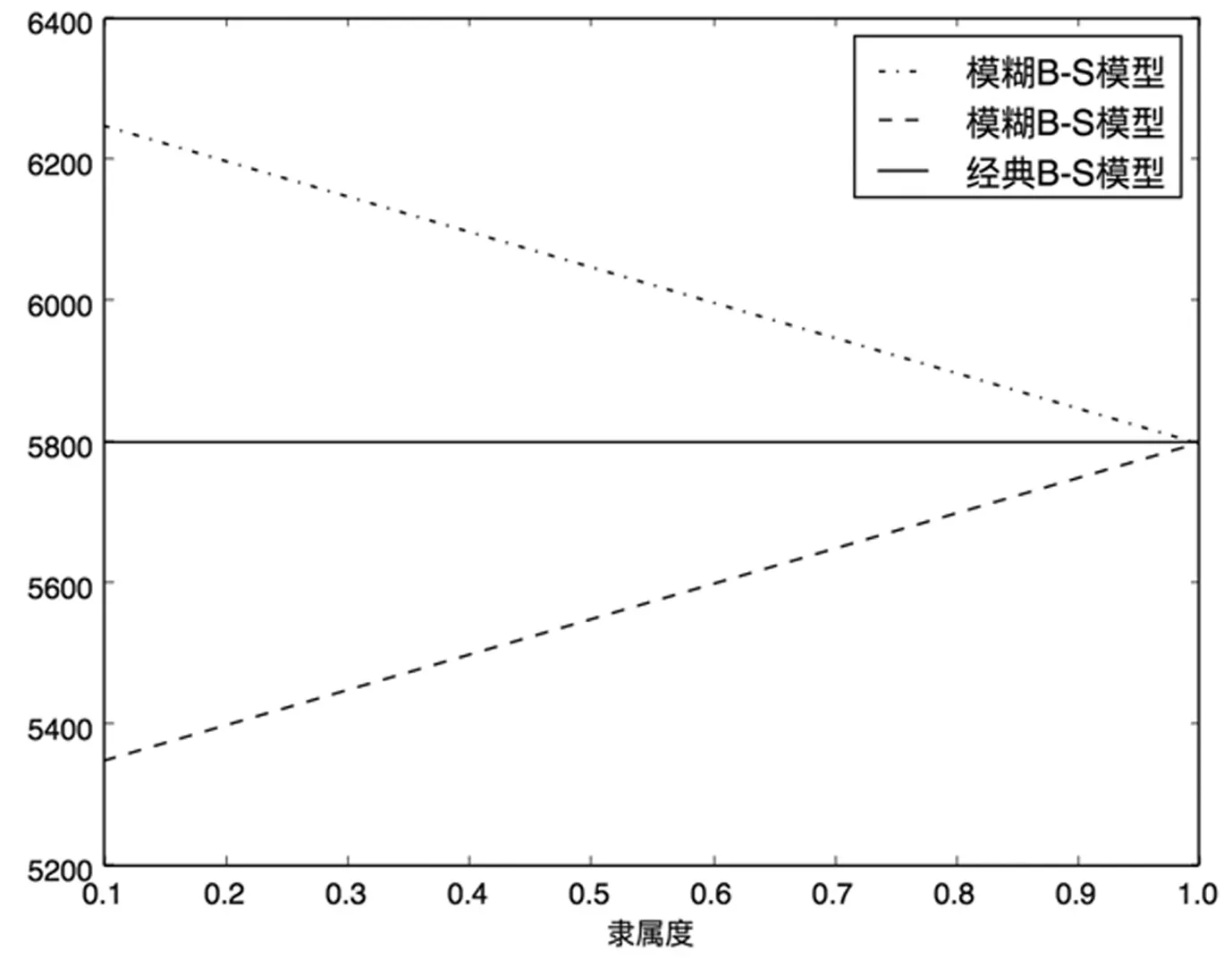
图2 隶属度图

VaR在险价值方法的运用，得到了钢铁类项目风险未来可能损失的最大值，这给项目投资者提供了统一的风险计量标准。而且VaR在险价值方法在测量项目风险中简洁明了，相对于以往诸多事前衡量的风险管理方法，其可以实现事前计算风险，这不仅方便了项目的投资者和管理者，而且为市场监管者提供了监测市场风险资本充足率的有效途径。

模糊B-S实物期权定价模型和VaR在险价值方法，能够在环境复杂多变、市场竞争日益激烈的情况下，对钢铁类实物期权进行合理的定价和风险量化，这促进了我国金融衍生品市场的发展，有利于实物风投项目综合风险控制的精准性。