多轴轮毂电机驱动电动车电子差速控制研究
2019-12-17靳立强田端洋
靳立强,田端洋,宋 琪
(吉林大学 汽车工程学院,吉林 长春 130025)
0 引 言
轮毂电机独立驱动的车辆,由于其省去了传统车辆的传动系统,同时每个车轮的驱动力矩独立可控、能实时准确反馈转矩转速等信息,使得整车传动效率大大提高,布置设计更为灵活,在稳定性、主动安全控制和节能方面比传统车辆更具显著的控制优势[1-2]。轮毂电机驱动车辆的电子差速器主要是为了代替传统车辆的机械式差速器,通过协调各驱动电机,保证车辆行驶时的操纵稳定性,它是轮毂电机驱动车辆必须解决的关键技术之一。
对电子差速控制的研究,学界主要有3个方面:对电机转速控制、对电机转矩控制、改变电机结构。翟丽等[3]所研制的“E-touring Car”电动游览车,根据阿克曼转向定理估算出各车轮理论轮速,从而完成闭环控制;F.J.PEREZ-PINAL等[4]利用建立参考模型方法,计算得到各车轮转速;LEE Ju-sang等[5]通过神经网络拟合转向时车轮转角及轮速关系,对车轮转速进行控制;何仁等[6]根提出一种基于车轮滑转率的模糊PID控制方法,对电驱动桥客车左右轮进行转速协调控制。这些研究都是基于不同的模型算法,目的是得到车轮期望转速,从而对各驱动电机进行转速控制。
单一转速控制对电机要求很高,同时不能适应路面不平或车轮滚动半径不等及车辆高速行驶时非线性动力学导致的差速问题。吴浩[7]以目标滑转率为控制目标,利用鲁棒控制器得到各轮的驱动转矩;张慧慧[8]和赵艳娥等[9]分别以轮胎滑移率为控制目标,采用滑膜控制,对两侧车轮转矩进行分配;葛英辉等[10]采用比例控制方法,利用可获得的信息估算出路面附着及车轮滑转率,进而完成驱动轮期望滑转率的计算,对各车轮驱动转矩进行再分配,实现差速控制的目的。
但当以滑转率为控制目标时,难以实现对小滑转率的实时监测和控制,同时目标滑转率估算受相关因素影响较大,难以准确估算,而单一的转矩控制也无法协调行驶过程中车辆受力的动态变化。A.KAWAMURA等[11]设计了一种特殊的多向电机以实现电子差速;JIN Liqiang等[12]则发明了一种单定子、双转子的感应电机来实现差速控制。通过改变电机结构方法,会大大减弱轮毂电机独立驱动优势,增加驱动系统复杂程度。
对多轴重型车辆而言,其自重及载重都很大,差速问题相对来说更为突出和严重。基于此,为了能满足各种行驶工况的整车差速性能要求,同时充分发挥轮毂电机独立驱动特点,笔者提出对电机采用转矩指令控制,但其不与油门相对应,而将转速进行反馈,利用其与期望值的差值输出各轮驱动转矩。从整车层面看,整体控制策略为功率控制,这与传统汽车的动力系统特性相对应。对各轮毂电机采用转矩指令控制、转速随动方法,各车轮根据实际受力状态建立平衡以得到转速,这保证了该控制策略具有较强适应性,能适应任意差速工况。
1 多轴电动轮汽车动力学
对于多轴车辆而言,由于其轴数相较于传统两轴车辆有所增加,其动力学问题也随之更为复杂。建模时不同自由度的整车模型会使仿真精度有所区别,理论上所考虑的整车自由度越多,仿真效果越好,但同时实际需要输入的参数也就越多;当无法得到相关参数时,整车自由度越多反而会影响其实际结果。对于文中所研究的8×8轮毂电机独立驱动电动车,其动力学模型考虑车身纵向、侧向、垂向、横摆、俯仰、侧倾全部6个自由度, 8个车轮的垂向跳动和转动自由度及一个车轮偏转自由度,共计23个自由度。
1.1 整车模型
对传统两轴车辆的动力学问题,大多是以经典的汽车线性二自由度理论模型入手,该方法对研究更为复杂的多轴车辆问题就显得不够精确。故笔者利用汽车系统动力学相关理论,将多轴汽车系统划分成车身、悬架、车轮和轮胎等几个主要部分,分别加以分析并建立模型,如图1。
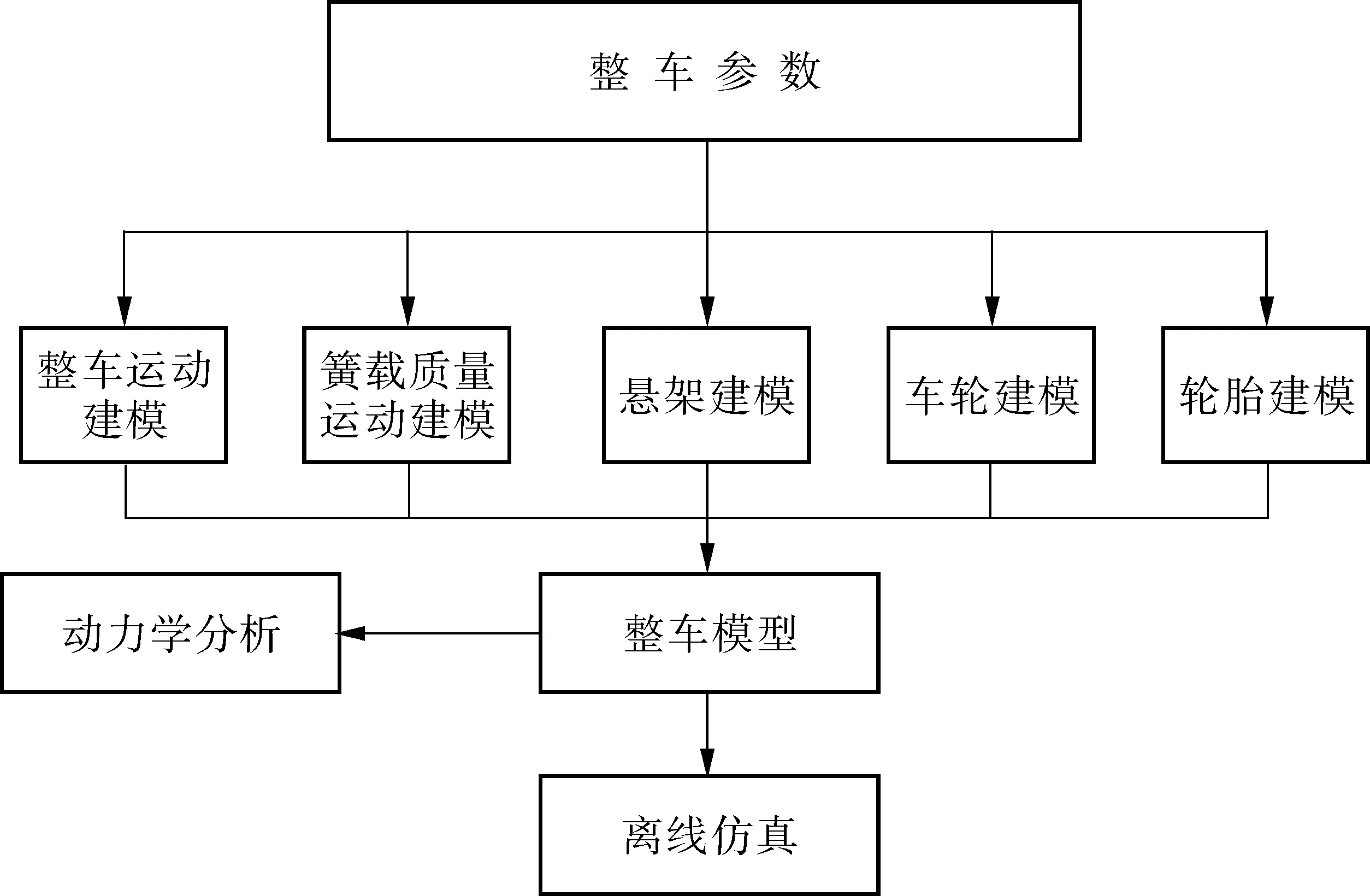
图1 多轴电动轮车辆建模流程Fig. 1 Modeling process of multi-axle electrical wheel vehicle
笔者针对车身运动6个自由度,建立坐标系。x轴正向沿车体纵向对称线,向前为正;y轴通过质心沿汽车横向位置,向右为正;z轴根据右手定则,竖直向下为正。根据车辆受力情况,综合考虑各方向运动之间的影响,如式(1)~(6):
纵向运动:
(1)
侧向运动:
(2)
垂向运动:
(3)
式中:u、v、w分别为车身纵向、侧向和垂向速度;r为车身横摆角速度;p为车身侧倾角速度;q为车身俯仰角速度;Mt为汽车总质量;Ms为簧载质量;h′为簧载质量质心至侧倾轴距离;Ff为总的行驶阻力;Fxi、Fyi、Fvi分别为车轮在纵向、侧向以及垂向上作用在悬架处的力;Bi为与悬架相关的参数。
俯仰运动:
(4)
横摆运动:
(5)
侧倾运动:
(6)
式中:Ixxs、Iyys、Izzs分别为簧上质量绕各方向转轴的转动惯量;Ai为悬架几何参数;T为轮距;L1、L2、L3分别为轴距;Lf、Lr分别为质心距2轴和3轴的距离;Φ为车身侧倾角。
对于车轮垂向跳动的问题,整车采用麦弗逊独立悬架,悬架模型如图2。
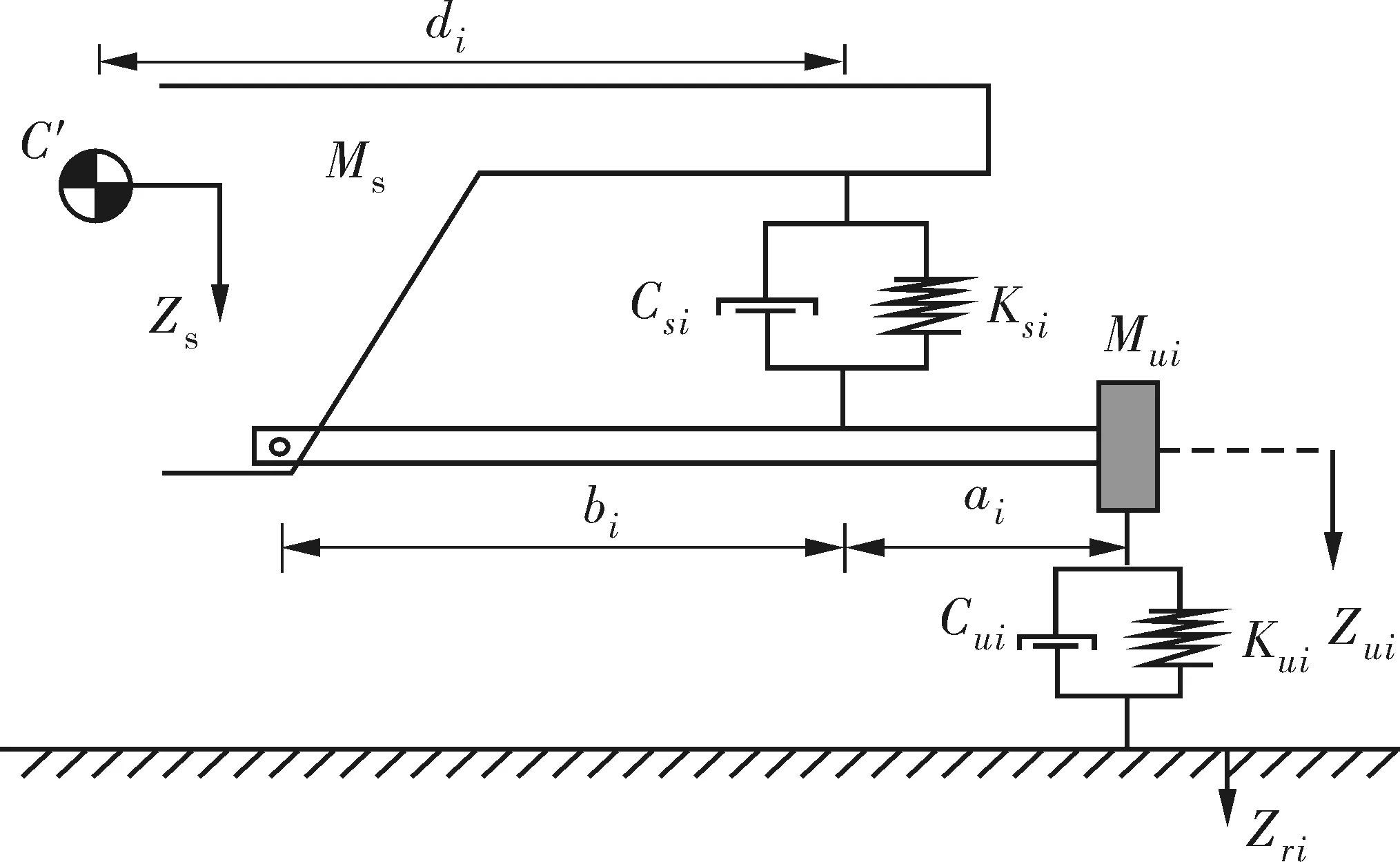
图2 悬架模型Fig. 2 Suspension model
图2中:C′为簧载质量质心;Kui、Ksi分别为各轮胎及悬架垂向刚度;Cui、Csi分别为对应阻尼;Zri为路面不平度在车轮处的输入;Zui为簧下质量质心高度;Zs为簧上质量质心高度。其车轮垂向跳动计算如式(7)。
(7)
式中:wui为车轮垂向运动速度;wri为车轮接触路面的不平度变化率。
整车为全轮转向,车轮的偏转自由度则是通过建立线性单轨多轴车辆转向模型,并根据阿克曼转向定理将各个车轮转向角联系起来,使得各车轮绕同一转向瞬心偏转。
1.2 车轮旋转动力学
差速问题实质是车轮转动时其边缘处线速度是否与该车轮轮心处的平移速度相协调,若不协调就会引起车轮拖滑或滑转,从而导致功率循环或车辆无法正常行驶。因此车轮旋转线速度和轮心处速度就是两个关键的物理量,那么就需要对车轮旋转动力学进行深入分析和讨论。
对于传统车辆车轮受力分析,一般只考虑车轮的驱动力矩、制动力矩及路面作用于车轮的反力,但此时并没有将悬架与车轮之间的作用考虑在内,因此无法解释从动轮运动。对于轮毂电机驱动车辆而言,由于各车轮驱动完全独立,显然要对车轮旋转动力学方程进行补充。
在分析传统车辆车轮受力基础上,当考虑悬架和车轮相互作用力及主动、从动轮问题时,动力学模型如图3。
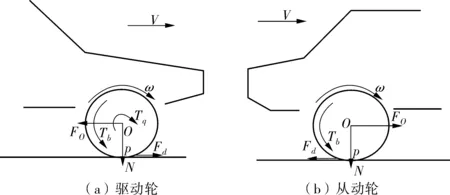
图3 车轮完整旋转动力学模型Fig. 3 Wheel complete rotation dynamics model
由图3可发现:悬架作用在轮心位置的力其实并没有在轮心处产生力矩,但它的变化会改变地面与轮胎之间的纵向力。对驱动轮来说,轮胎纵向力可以由“魔术公式”计算得到;但对从动轮而言,由于其滑转率在非制动时为0,传统汽车车轮旋转动力学则不能表示其运动状态。故需对车轮旋转动力学方程进行补充,如式(8):
(8)
式中:Iw为车轮转动惯量;Tq为车轮驱动力矩;Tb为制动力矩;rω为车轮滚动半径;Fd为轮胎与路面之间纵向力;Mω为车轮质量;ωo为车轮转速;Vω为车轮轮心处速度。
式(8)中:方程右侧最后1项为相比传统汽车车轮旋转动力学的补充项,其含义为由轮轴对从动轮轮心处的作用而在地面上形成的反力。经过这样补充,式(8)可同时表示驱动轮及从动轮动力学问题。其中ξ为作用系数,其取值如式(9):
(9)
在驱动车轮或制动车轮时,Fd≠0,则式(9)与传统汽车车轮旋转动力学方程相同;而对从动轮而言,非制动时由于其滑转率为0,无法求出车轮纵向力,则Fd=0,此时从动轮轮心绕接地点p的角加速度可用式(10)表示:
(10)
车轮旋转角加速度和轮心绕接地点处的角加速度相等,则式(10)可表示为式(11)~(12):
(11)
(12)
对车轮轮心进行转矩分析,式(10)两侧同时乘上车轮转动惯量,整理后即可得到完整的车轮旋转动力学方程。补充后的方程能同时反映驱动轮受驱动、制动和路面的作用及车体与车轮相互作用对从动轮运动影响。
2 控制策略制定
机械差速器一般存在1%~5%的内阻,这使得两侧车轮驱动力实际并不完全相等,故对于传统车辆能够实现差速,除机械差速器外,很重要的一点是在于整个动力系统采用功率传递,这保证了虽然两侧半轴转速和差速器壳的转速存在固定关系,但这3者都是根据实际工况动态变化。发动机传给车轮的为功率而非单一转矩或转速,各车轮根据路面负载从而实现自适应差速。那么电子差速实现原则也应模拟传统车辆从动力系统到差速器功率分配特性,以保证各车轮能够适应任意行驶工况。
2.1 控制策略
电动轮驱动汽车的驱动电机与车轮直接相连,由于路面负载的未知性,无法对电机转矩与转速同时控制(功率控制)。选择以驱动转矩为控制参数对电机进行控制,不进行转速控制,其转速根据车轮实际受力情况自行得到,因此每个车轮就增加了一个转动自由度。此外,当车轮驱动转矩没有超过路面附着极限时,路面摩擦力对轮心处力矩必定与车轮驱动转矩相等,而同时滑转率也必定处于附着特性的稳态区,车轮不会出现过度滑转或拖滑。由于车轮转速随动,整车的电子差速控制问题归根结底转化为对整车的车速控制问题,这里采用车速反馈法解决,防止电机转速失控,具体控制流程如图4。
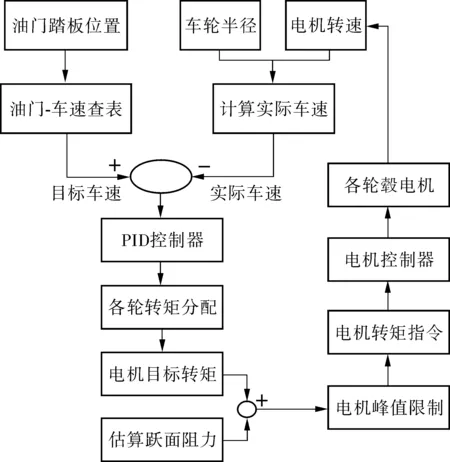
图4 自适应电子差速控制模块流程Fig. 4 Self-adaptive electronic differential control module process
以油门踏板开度传感器为控制输入,反映驾驶员期望的车辆驱动情况,利用该信号查表得到对应的期望车速值,再与轮速传感器或轮毂电机反馈的轮速信号计算出的实际车速做差,将偏差值输入到PID控制器中,进而输出驱动电机的目标转矩,根据估算的行驶阻力进行一定的补偿,在峰值转矩及功率的限制下发送给轮毂电机控制器,对各车轮进行驱动控制。车轮实际转速由电机驱动转矩和实际车轮受力的平衡点决定,并反馈给整车控制器实现闭环,使得油门踏板同时控制车速(电机转速)和电机转矩,从整车层面看即为一个功率控制模式。
2.2 电子差速控制系统
整个控制系统主要包括3部分:主控制器、各轮毂电机及控制器系统、CAN总线通讯网络。图4中:自适应电子差速控制流程,主控制器采集油门踏板位置信号及车轮转速信号分别计算出目标车速和实际车速,进而分析计算得到实际应该提供给各车轮的驱动转矩,并将此信号发送给各轮毂电机控制器。各电动轮及其控制器是整个电子差速控制系统的执行部分,由于电机直接作用于车轮,相关数据能实时准确地进行反馈,响应迅速。CAN总线则是负责连接电子控制单元与执行部分,及时准确的将控制信号传递到电机控制器。
3 离线仿真及台架试验
3.1 整车参数
仿真中采用四轴轮毂电机全轮驱动(8×8)电动车,此外整车还采用全轮线控转向技术,1~4轴采用逆相位转向。仿真中整车的相关参数如表1。
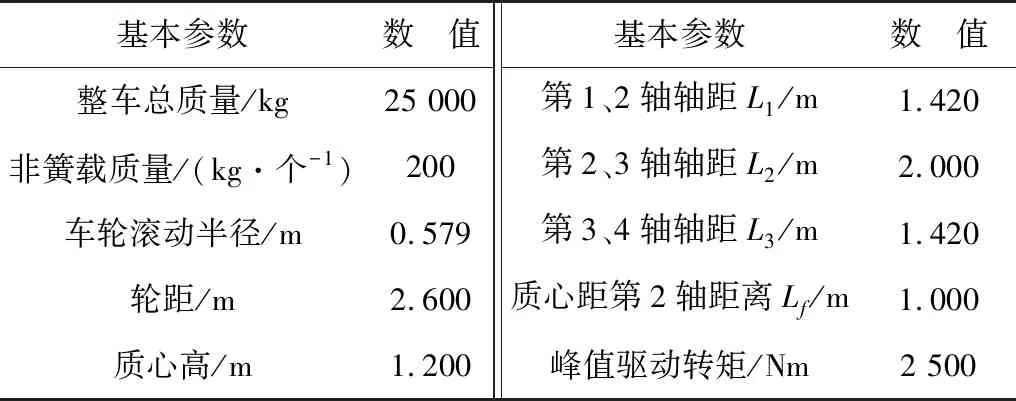
表1 8×8整车主要参数Table 1 Main parameters of the 8×8 whole vehicle
3.2 离线仿真试验
车辆差速问题主要是指车轮转动时轮边处线速度不能与该车轮轮心处平移速度相协调,那么可将出现差速的工况大致归为3类:① 转向行驶时,因为车辆发生横摆运动,这导致各车轮轮心处的加速度产生差异,使得各轮轮速不同;② 行驶于不平路面时,由于各轮轮心经过的轨迹长度不同,而导致各轮转速不同;③ 当各车轮滚动半径不同时,各轮轮心经过的轨迹长度虽然相同,但由于车轮半径不同,导致各轮转速不同。
3.2.1 转向工况
整车由静止开始加速,目标车速40 km/h,在20 s时对左前轮输入0.1 rad的阶跃转向角,使整车逆时针转向行驶。图5为仿真时的整车车速变化。
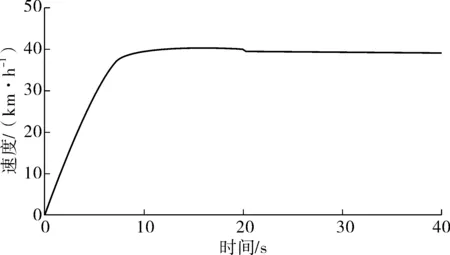
图5 整车纵向速度Fig. 5 Longitudinal velocity of the whole vehicle
由图5可看出:在15 s时整车达到车速为40 km/h的匀速行驶工况;20 s时方向盘输入阶跃转向角,由于整车行驶阻力增大,从而导致车速下降,这与实际工况相符。
图6表示各车轮转角值,基于阿克曼转向定理,根据左前轮转角得到其他各车轮实际转角。
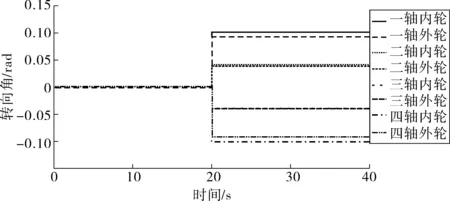
图6 各车轮偏转角Fig. 6 Wheel turning angle
图7分别为各车轮轮心速度和旋转线速度与时间的关系。输入向左的方向盘转角后,由于整车发生横摆运动,这导致各轮心速度发生变化,而各车轮旋转线速度能相应较好的与轮心速度相协调。右侧车轮速度普遍大于左侧车轮速度,即转向时外侧车轮速度大于内侧车轮速度,这与实际情况相符。

图7 速度与时间关系Fig. 7 Relation between speed and time
图8为各车轮滑移率变化。由图8可看出:各车轮均没有发生明显滑移或者滑转,也就代表着各车轮旋转线速度与轮心速度实现了较好协调。此外转向行驶时,发生载荷转移,各车轮载荷发生改变,而各车轮驱动转矩仍相等且没有超出路面附着极限,那么路面摩擦力必然与其平衡,因此各车轮滑转率稍有不同。
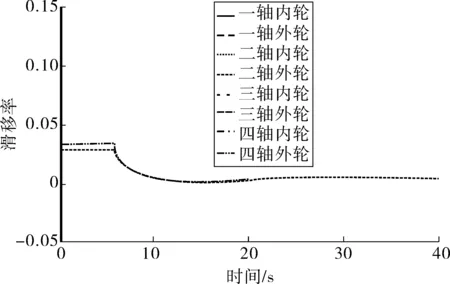
图8 滑移率变化Fig. 8 Slip rate variation
整车行驶轨迹如图9。由图9可看出:自适应电子差速控制能够协调转向行驶时的轮速,使车辆按照驾驶员期望轨迹行驶。
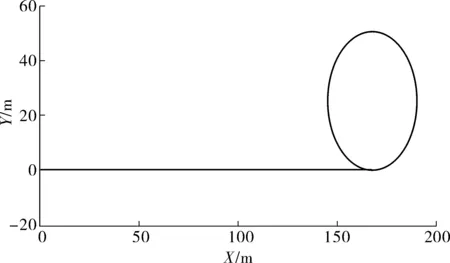
图9 整车行驶轨迹Fig. 9 Driving track of the whole vehicle
图10为各车轮受到的地面纵向力变化。由图10可看出:左侧车轮地面纵向力均大于右侧车轮,那么在各车轮驱动转矩相同情况下,左侧车轮即内侧车轮转速均要小于同轴的外侧车轮,这与实际相符。在控制中只对轮毂电机采用转矩指令控制,且各车轮驱动转矩相同,那么车轮转速仅随地面纵向力变化。而地面纵向力其中也包含了车辆内部之间作用力,比如车轮与车体之间的相互作用力,其二者的动态协调应是实现各车轮差速的根本条件。而自适应电子差速控制使车轮根据实际受力状态建立平衡,得到轮速,这就能保证整车内部各系统间的作用力相互协调,从而适用于任意行驶工况。
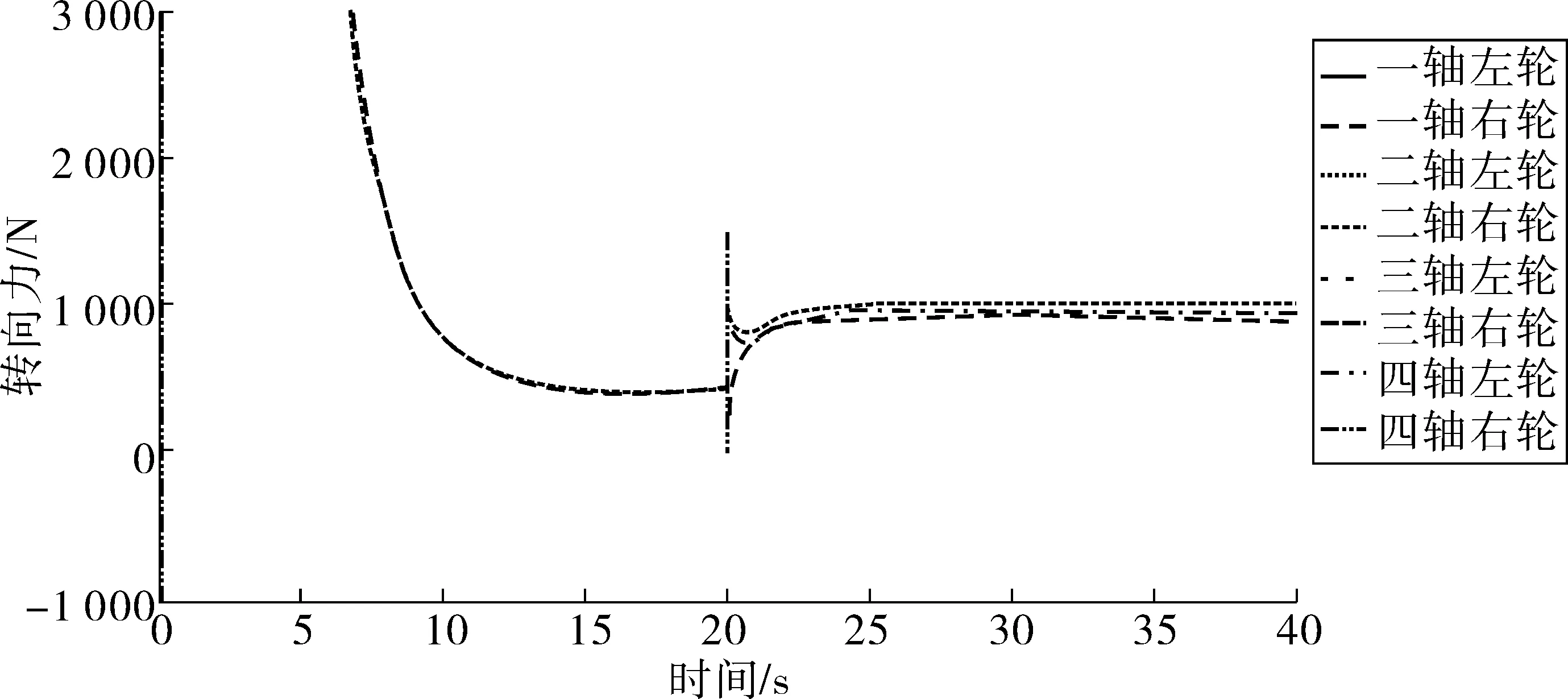
图10 各车轮地面纵向力Fig. 10 Longitudinal force on the ground of each wheel
3.2.2 不平路面工况
整车从静止加速到40 km/h匀速行驶,第19 s时第1轴左侧车轮驶入正弦变化的不平路面;2~4轴左侧车轮依次驶入,右侧车轮行驶于水平路面,所得行驶性能曲线如图11。

图11 行驶性能曲线Fig. 11 Driving performance curve
图11(c)、(d)为各车轮轮心速度与车轮旋转线速度变化。从第1轴左侧车轮遇到不平路面开始,所有右侧车轮受左侧车轮的速度影响也开始变得时快时慢;由其速度变化曲线可看出,这些车轮能自适应由于单侧车轮路面不平度引起的“不适”。
图12分别为各车轮轮心垂向位置变化以及垂向速度变化,车轮沿地面做近似纯滚动而没有出现拖滑。在车轮刚接触正弦路面时,车轮垂向速度存在一个突变,这与实际情况相符,所建模型很好模拟了车轮在不平路面行驶时的运动状态。

图12 车轮轮心位置和速度变化Fig. 12 Variation of wheel center position and speed
3.2.3 车轮半径不等工况
车轮半径参数如表2。改变第1、2轴这4个车轮滚动半径,使其各不相同。汽车由静止开始加速,目标车速为40 km/h,然后保持匀速直线行驶,仿真时各车轮驱动转矩始终相等。
图13分别为汽车各车轮转速及滑移率变化情况,行驶过程中各车轮并没有出现拖滑。但由于各车轮的实际滚动半径不等,这导致了各车轮转速有所差别,各车轮在此过程中实现了自适应差速。
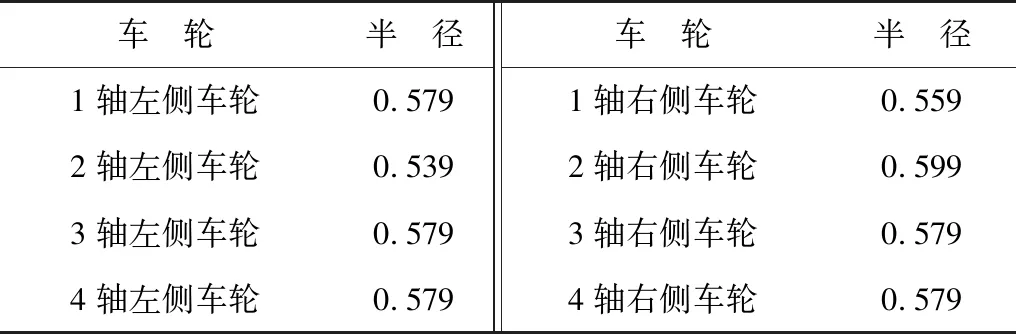
表2 车轮半径参数Table 2 Wheel parameter m

图13 各车轮转速和滑移率变化Fig. 13 Variation of wheel rotation speed and slip rate
图14分别为各车轮旋转线速度与轮心速度的变化曲线。在各车轮滚动半径不等工况下,车轮旋转线速度和轮心速度能相协调,各个车轮实现了很好地自适应差速性能。

图14 车轮轮心速度和旋转线速度曲线Fig. 14 Curve of wheel center velocity and rotation velocity
3.3 性能评价
差速工况主要包括:转向、车轮半径不等和路面不平,故要验证差速性能是否理想。要验证这3种工况下各轮旋转线速度能否与各轮轮心速度相协调,即车轮运动能否满足式(13)、(14):
ui=ωi·rwi
(13)
(14)
式中:ui为各车轮轮心处平移速度;ωi为各车轮旋转角速度;rwi为各车轮实际滚动半径;Si为车轮轮心处平移距离。
若车辆实际各车轮运动学状态满足式(14),则说明车辆不存在差速问题,或差速问题已得到解决。则定义第i个车轮轮心理论行驶距离Si与其实际滚过距离Xi的比值为ηi,则有式(15):
(15)
当ηi=1时,说明该车轮旋转线速度与轮心速度保持一致,没有发生拖滑或滑转现象,二者能很好的进行协调,差速性能良好;若ηi<1时,说明轮心理论行驶距离小于车轮实际驶距离,意味着车轮在行驶过程中发生滑转,使得轮心行驶距离偏小;若ηi>1时,则说明该车轮发生了滑移;故评价车辆电子差速性能良好的标准即ηi≈1。以上述转向工况仿真为例,利用此法进行评价(表3),为保证数据可靠性,排除启动加速过程中车轮滑转影响。表3为加速过程完成后15~40 s所对应仿真工况结果。
当ηi稍小于1时,说明各车轮发生了轻微滑转。同时各车轮轮心行驶距离与实际滚过距离误差百分比均很小,说明在该工况下,各车轮差速性能较好。同样对其他两种工况进行分析,可发现其采用自适应电子差速控制的各车轮理论与实际行驶距离误差均小于0.5%,证明达到了较好的差速控制效果。
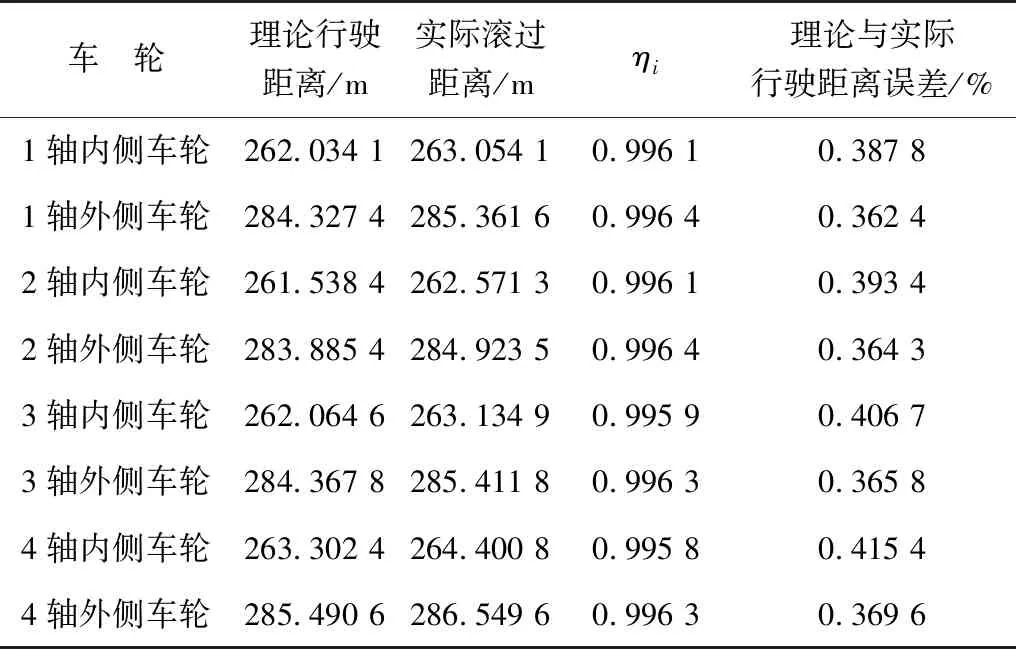
表3 阶跃工况各车轮滚动参数Table 3 Rolling parameters of each wheel in step condition
3.4 控制性能对比
为进一步证明笔者所提出的观点,将其与转速控制进行对比。转速控制主要依据阿克曼转向原理,在转向行驶时使各车轮转速满足绕转向中心行驶的几何及运动学约束,转向中心由车速与方向盘转角计算获得。
图15(a)为自适应电子差速控制与转速控制各车轮滑移率变化对比。当目标车速为40 km/h,方向盘为20 s时,阶跃输入转角为0.1 rad。这两种控制下各车轮滑移率均极小,相较而言转速控制滑移率略大,但各车轮均没有发生明显滑转或滑移。
图15(b)为车速80 km/h时的滑移率对比曲线。此时转速控制下各车轮发生了一定滑转,差速性能变差,这主要是因为高速或较大转向角时汽车相关运动已不能用线性方程表示,各车轮实际需求转速与计算值相差较大,致使转速控制差速性能变差,同时其无法针对路面不平及车轮滚动半径不等工况。
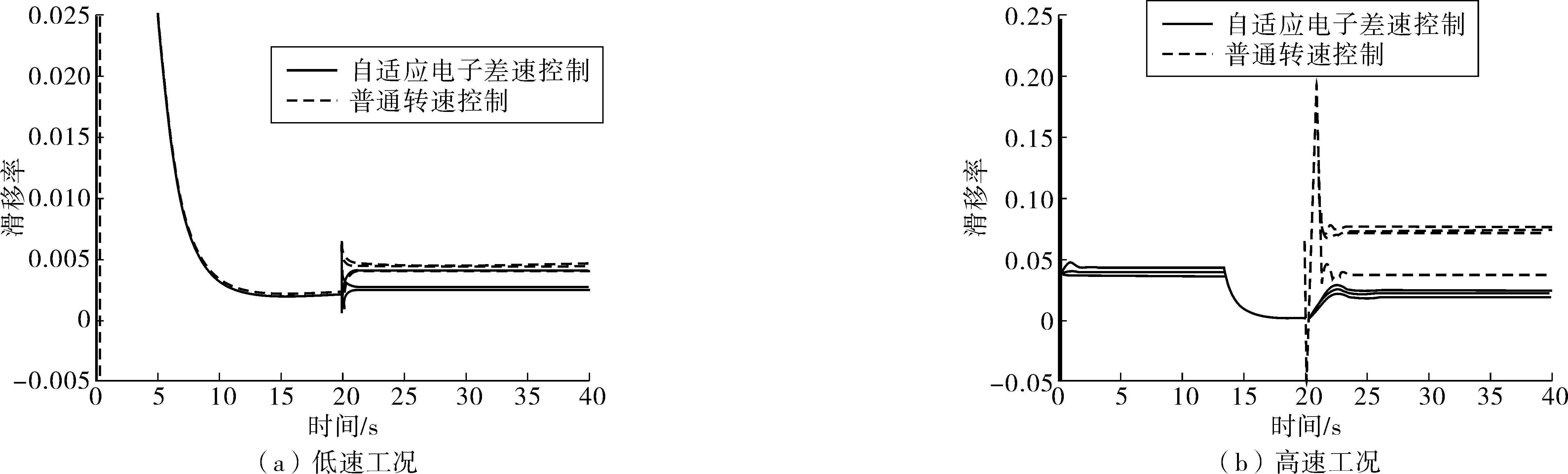
图15 低、高速工况滑移率对比Fig. 15 Comparison of slip rate under low and high speed conditions
3.5 台架试验
为进一步对控制策略进行验证,同时为后续实车试验验证等相关测试做准备,笔者又进一步进行了台架试验。考虑到控制模型所需外部输入,台架中接入方向盘转角传感器与油门踏板传感器。利用Truck-Sim对整车模型进行设置,具体参数设置与离线仿真相同,并将其下载到快速原型控制器Simulator中,控制模型下载到TTC作为整车控制器,具体架构如图16。
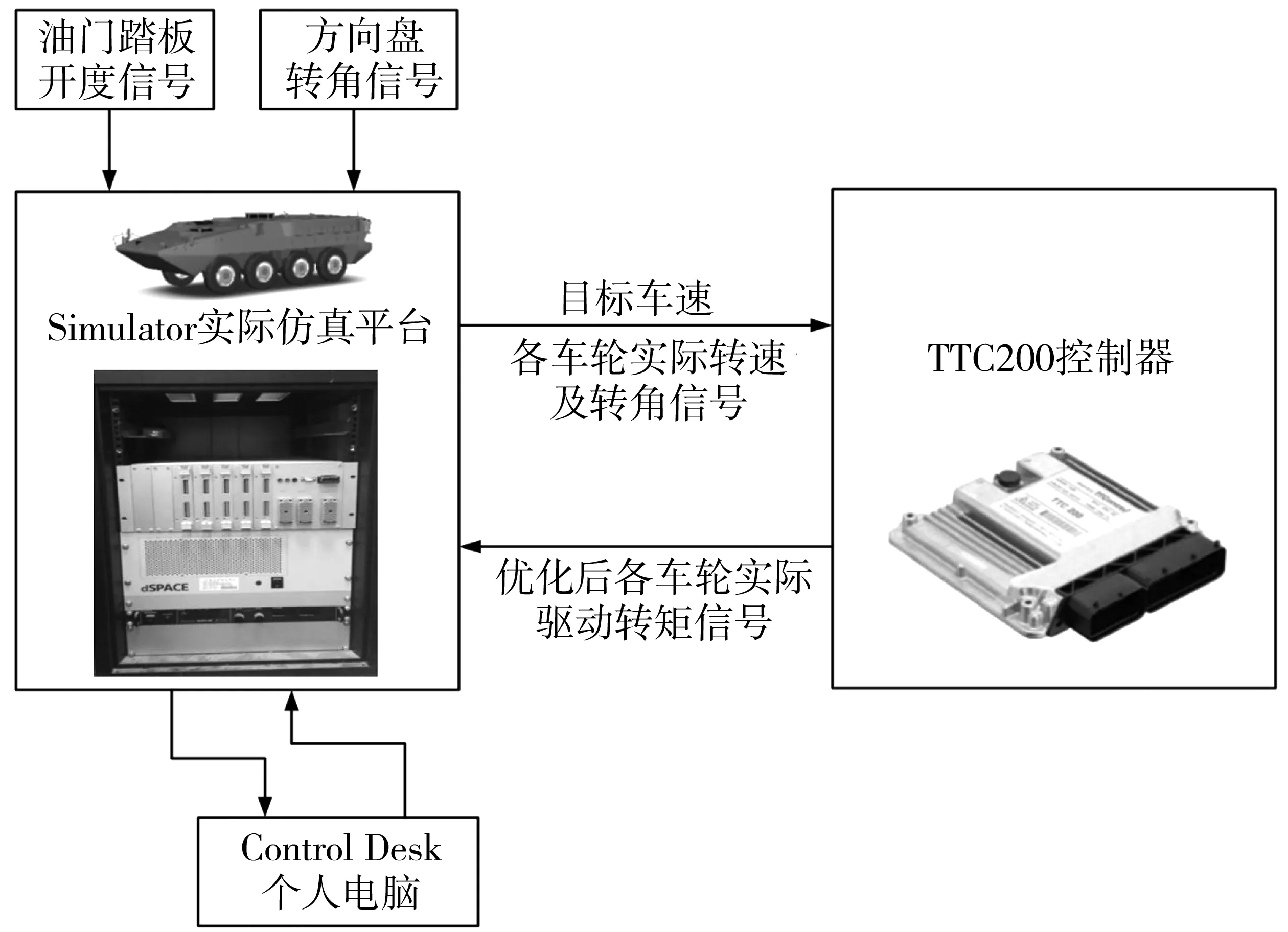
图16 硬件在环架构Fig. 16 HIL frame diagram
通过踩下油门踏板,使车辆由静止加速到60 km/h左右,并保持油门踏板开度。手动左右转动方向盘,考虑到整车行驶稳定性,车辆只采用1、2轴转向,方向盘转角幅值在30°~35°,方向盘及各车轮实际转角如图17。
图18为台架试验过程中各车轮轮心速度及车轮旋转线速度随方向盘转动的变化曲线。这二者受方向盘转角不断变化影响,并在目标车速附近波动;这两者变化趋势相同时,即能实现较好的协调。图19为各车轮滑移率变化,由此发现各车轮滑移率均很小,没有发生明显拖滑或滑转,这代表台架试验的结果也是积极的。

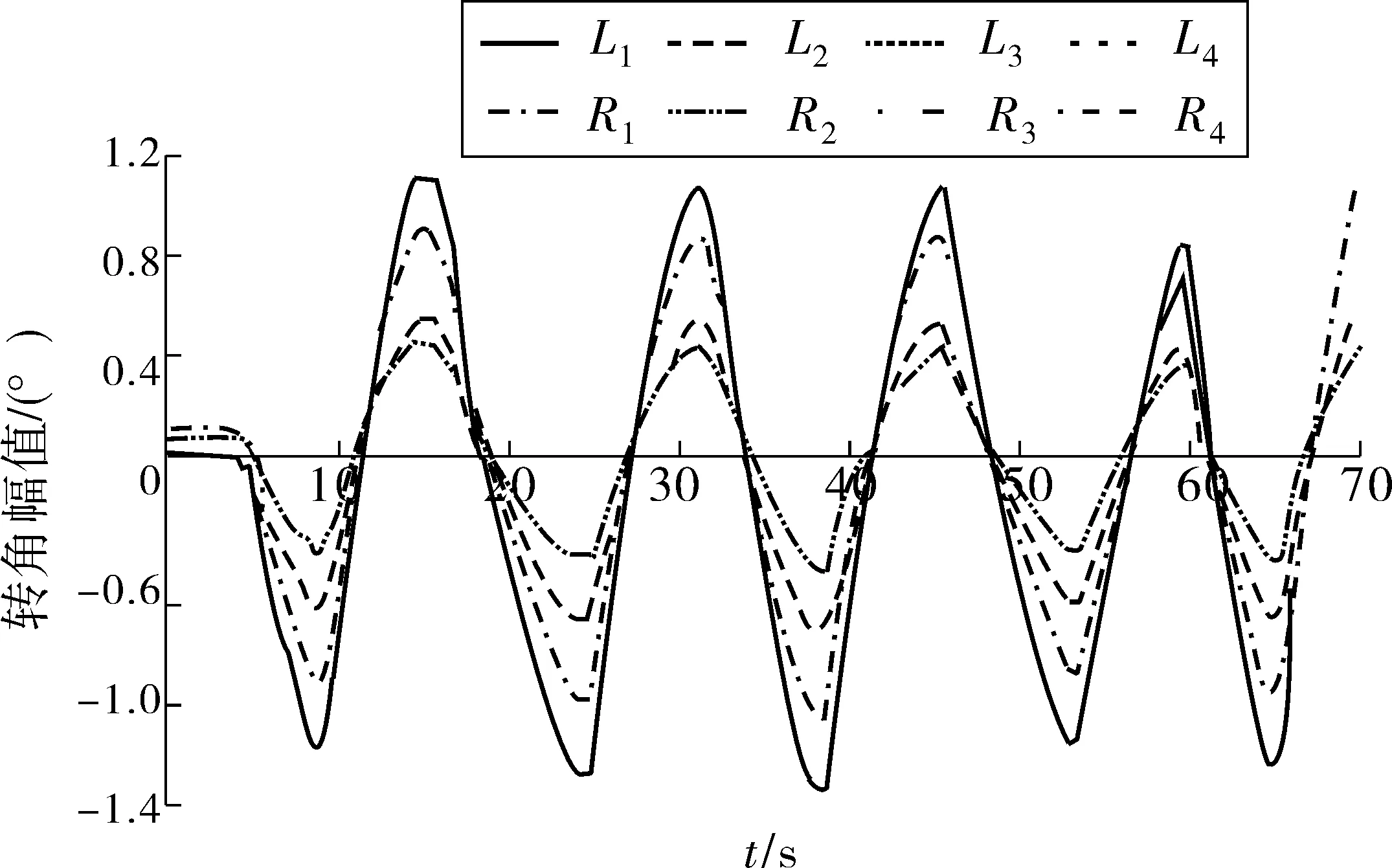
图17 方向盘和车轮转角曲线Fig. 17 Curve of steering wheel and wheel turning angle
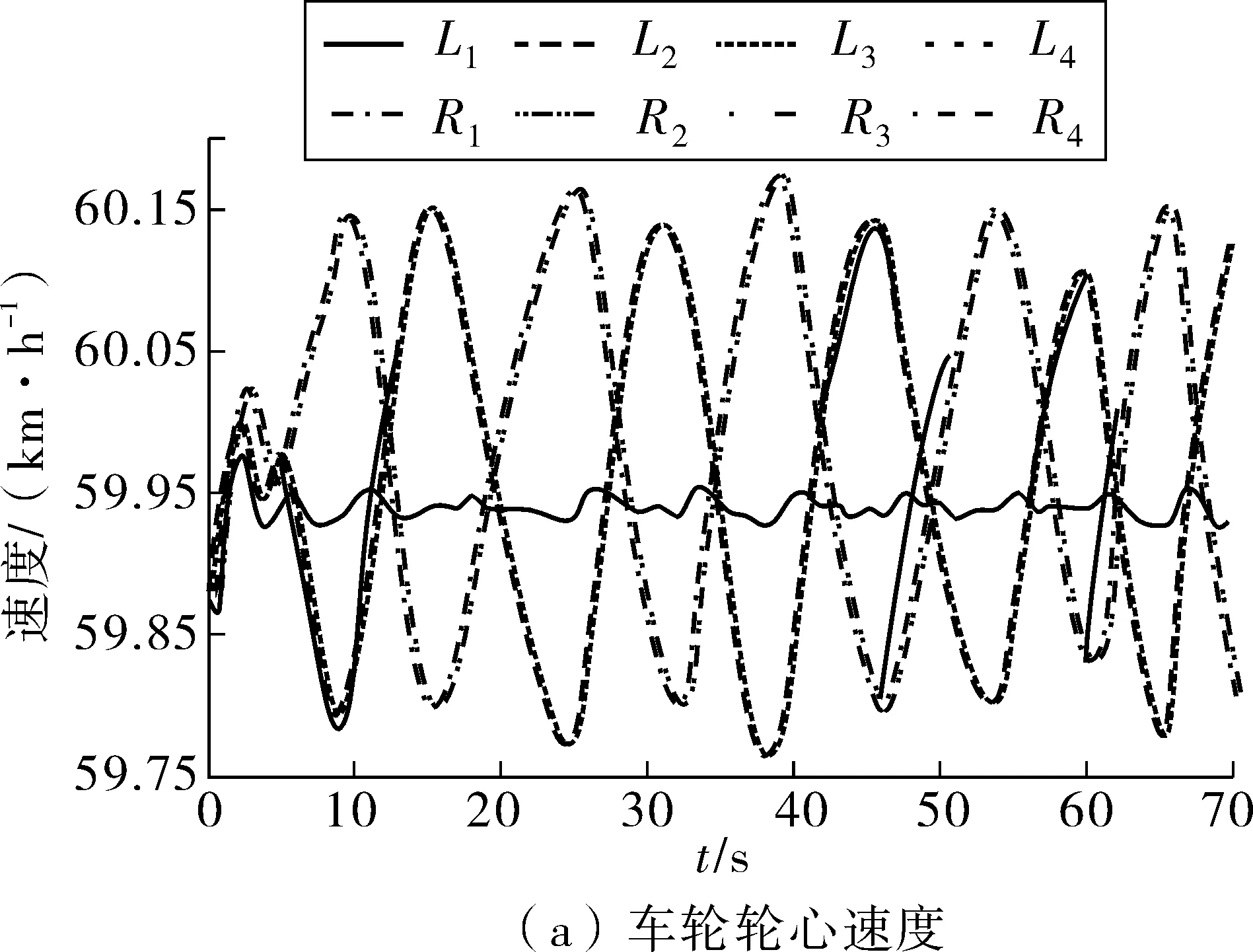
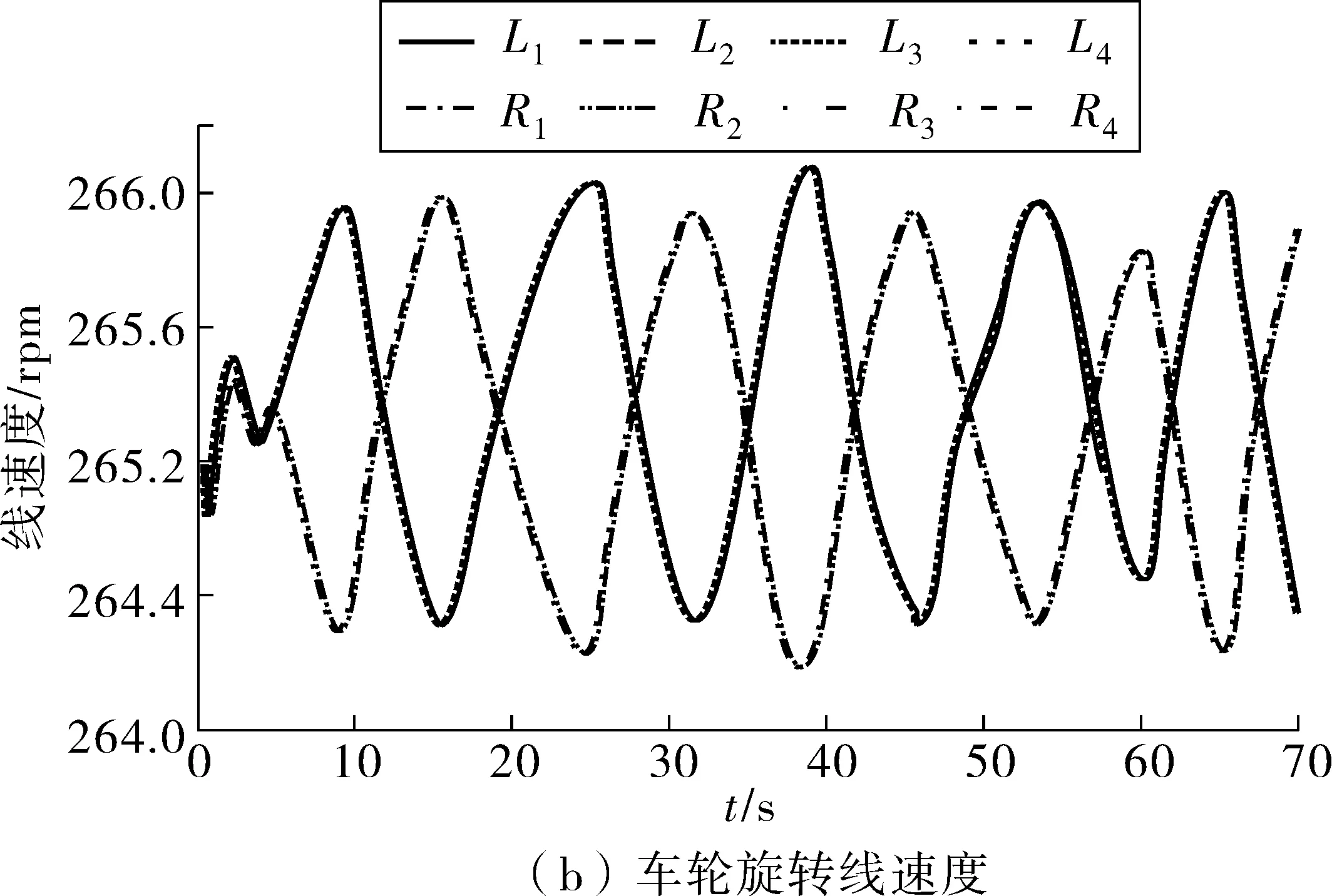
图18 车轮轮心速度和车轮旋转线速度曲线Fig. 18 Curve of wheel center velocity and wheel rotation velocity
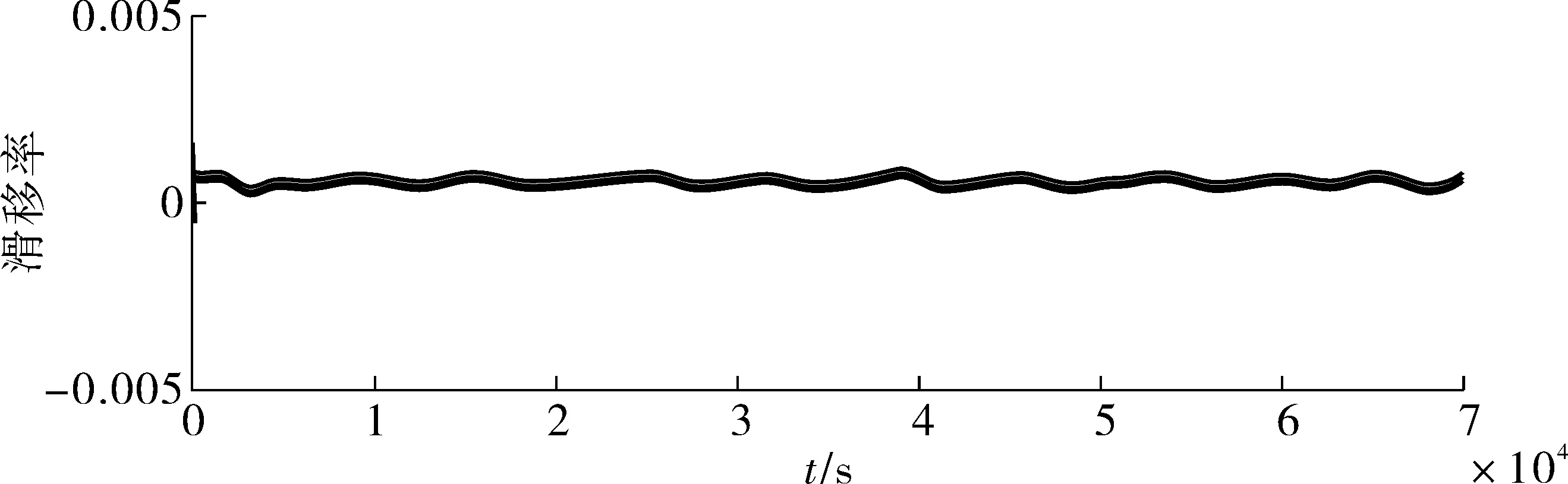
图19 各车轮滑移率Fig. 19 Wheel slip rate
4 结 论
1)笔者提出自适应电子差速控制策略,并对各驱动电机采用转矩指令进行控制,转速随动方法,能使多轴轮毂电机驱动电动车各车轮轮心速度与车轮旋转线速度在转向、不平路面及车轮滚动半径不等这3种工况下实现相互协调。利用离线仿真及台架试验结合所提差速性能评价方法,证明该控制策略所实现的差速性能较好,各车轮理论与实际行驶距离误差不超过0.5%,有效避免各车轮因差速问题出现明显的拖滑或滑转现象。
2)相较于其他电子差速控制方法,自适应电子差速控制主要特点在于:其能适应任意行驶工况,如路面不平、车轮滑移率较小等,使各车轮根据其自身受力状态而自由转动,实现较好的差速性能,鲁棒性较强。
3)由于自适应电子差速控制实际对各车轮的驱动转矩相同,车轮转速完全是由其自身受力状态而决定,因此自适应差速控制策略对仿真中涉及的这3种工况而言无论是低速还是高速均适用。
