基于微波热裂法的陶瓷切割技术

2019-12-17王向伟王海龙

中国机械工程 2019年23期

王向伟王海龙王扬

1.哈尔滨商业大学轻工学院，哈尔滨，1500012.哈尔滨工业大学机电工程学院，哈尔滨，150001

0 引言

平板陶瓷如碳化硅、氧化铝等具有的优质力学性能和物化属性，使其在航空航天、装备制造和电子器件等行业中得到了广泛的应用。平板陶瓷切割是陶瓷产品重要制造工艺之一。目前广泛采用的切割方法有机械切割[1]、激光熔融切割[2]、等离子切割[3]和水射流切割[4]等。利用上述方法对陶瓷材料进行切割时，会不可避免地将切割轨迹周围的大量材料同时去除，因此在切割表面上会遗留各种加工痕迹和微裂纹，得到的切割轨迹及加工表面质量较差，降低了产品边缘的力学性能和产品在使用过程中的可靠性，且加工过程产生大量的切屑将造成严重的噪声污染、切削污染。

与上述切割方法不同，热裂法是利用热应力诱导材料边缘初始裂纹沿预定轨迹扩展以完成平板陶瓷的切割加工。在热裂法切割加工过程中无材料去除，切割表面无加工痕迹和微裂纹，最大程度地维持了材料本身的原貌，将材料整体的弯曲强度提高了近1.8倍[5]，保证了陶瓷产品的高可靠性要求。此外，由于热裂法切割过程中无切屑产生，不产生噪声和切屑污染，切割过程和结果更绿色环保，因此在可持续加工技术领域中得到了越来越多的关注和研究[6-7]。

热裂法的发展总是伴随着热裂法热源形式的发展[8]。国内外学者尝试利用多种波长和形状的激光热源去获得更高的切割质量[9]、更大的切割厚度[10]、更快的切割速度[11]。激光热裂法已成熟地应用于玻璃切割中，KANG等[11]变换了激光光束的形状(采用更长的椭圆形光斑)和冷却介质(采用液体冷却)，使得高速切割夹层玻璃得以实现，他们研制出的系列产品已在市场中得到了广泛应用。

激光热裂法在陶瓷切割中的应用却鲜见成功的报道。TSAI等[12-14]尝试利用激光对氧化铝陶瓷进行热裂切割，虽获得了较好的切割轨迹，但热损伤层的出现，使得切割表面产生了大量微裂纹，这背离了热裂法研究的初衷。此外，激光的高成本也限制了激光热裂法的进一步应用。

本课题组在前期研究中已成功采用椭圆形微波热源对玻璃和碳化硅陶瓷进行了热裂切割[15]。虽然椭圆形微波热源有利于直线切割加工玻璃和碳化硅陶瓷，但是椭圆形微波热源并不能实现有效的曲线切割。为进一步发展微波热裂法，本文采用圆形微波能束代替激光作为热裂法热源，来实现陶瓷材料的圆波束微波热裂切割，基于微波热裂法原理，采用波导同轴转换方法，构建了圆形微波能束的技术模型，并研制了微波热裂切割实验装置；对该装置形成的微波热源进行了表征，并得到了微波热源的表征方程；最后利用微波热裂切割实验装置对玻璃、碳化硅、氧化铝和氧化锆四种陶瓷进行了热裂切割，通过分析切割轨迹和表面，定性揭示了微波热裂切割陶瓷的机理。

1 微波热裂切割技术原理及实验装置

微波热裂法切割原理见图1a。利用入射微波束沿预定轨迹从工件边缘向工件内部扫描加热，工件将产生不均匀温度场及相应热应力场，该热应力场将在工件边缘初始裂纹尖端处产生应力集中。当初始裂纹尖端应力集中因子KC大于或等于工件断裂韧性KIC(即KC≥KIC)时，裂纹将沿最大能量释放率方向扩展。通过调整微波能束扫描方式(扫描路径、速度、功率及微波能束形状)可产生合适的热应力分布场，以控制裂纹沿预定轨迹扩展。当裂纹沿预定轨迹扩展至工件任意边缘处时，整个切割加工过程得以完成。

微波能束的聚焦技术是实现图1a所示的微波热裂切割加工原理的关键技术。基于波导同轴转换原理建立的圆能束微波热裂切割陶瓷技术模型见图1b，其中控制器控制磁控管在激发波导内部产生所需功率的TE01微波场。激发波导入口封闭，出口与环形器入口相连接。环形器将激发波导内部的微波单向传输至与其出口相连接的波导-同轴转换组件，并防止反射微波损伤磁控管。与环形器相连接的矩形波导出口处连接有可调节的短路活塞。通过调节短路活塞在矩形波导内部的位置，可激发波导内部的微波产生谐振态。同轴波导内芯则在谐振态最强处将谐振微波能量耦合并传输至同轴内芯末端。被传输的微波在同轴内芯末端产生辐射近场。若将工件放置在辐射近场内部，吸波陶瓷或吸波媒质将有效地吸收微波能量并将其转化为热能。吸波陶瓷在水平方向移动，可控制微波能束对吸波陶瓷沿预定轨迹的扫描加热。

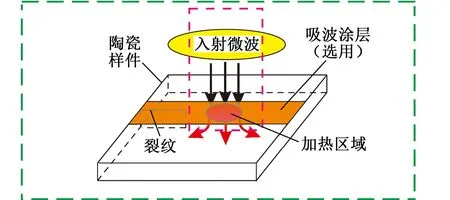
(a)微波热裂法原理

(b)圆能束微波热裂切割技术模型图1 微波热裂法原理及圆能束微波热裂切割技术模型Fig.1 The principle and model of thermal controlled fracture method by using microwave

基于图1的原理及技术模型，开发出了基于波导同轴转换原理的微波热裂切割陶瓷实验装置，见图2。微波源集成了图1中的微波源控制器和磁控管。激发波导采用BJ26波导，并深入至微波源内部将磁控管产生的微波传输至环形器。环形器与同轴聚焦装置连接，同轴聚焦装置集成了图1中的同轴外套筒、同轴内芯、矩形波导和短路活塞。短路活塞由螺母丝杠组成。同轴聚焦装置内芯末端放置工件，工件放置在三维移动平台上，实现微波扫描轨迹和扫描速度的控制。垂直方向可手动调节，可调节工件与同轴内芯末端的距离。

图2 微波热裂切割装置Fig.2 The cutting equipment with microwave based on thermal controlled fracture

本实验工件的尺寸如下：钠钙玻璃和碳化硅陶瓷板的尺寸均为100 mm×100 mm×3 mm，氧化铝和氧化锆陶瓷板的尺寸均为100 mm×100 mm ×1 mm。上述工件的切割制备中，在边缘处残留有许多微裂纹(长度约0.1 mm)，残留的微裂纹可作为工件热裂切割加工用初始裂纹。工件初始裂纹的长度及其所在位置对裂纹扩展轨迹精度的影响较大，但对切割表面质量的影响较小，对工件初始裂纹的长度及其所在位置方面的机理进行探讨需要较大篇幅，本文主旨在于对所构建的圆能束微波热裂切割技术模型进行验证，因此本文不再赘述上述机理。

2 微波热源表征

对图1b中同轴内芯末端产生的微波能束引起的热源进行准确表征，是理解微波热裂切割陶瓷机理的关键。为对此热源进行定量的描述，本文采用电磁生热仿真结果与测温实验结果进行对比的方法对该热源的拟合模型进行验证。首先利用电磁仿真得到该热源的表征方程，采用有限元仿真分析方法分析该热源作用下的温度场；然后采用光纤测温方法对同等条件下的工件加热区域进行样本点测温实验，并与仿真得到的温度场进行比较，从而验证所表征的热源方程的准确性和适用性。

2.1 热源表征仿真模型及理论基础

基于图1b所示的技术模型，取其中影响波导-同轴耦合方式和效率的关键结构和尺寸，建立图3所示的仿真模型。该模型由同轴内芯、同轴外套管、BJ26矩形波导和工件组成。在矩形波导左侧输入功率Pin=1 kW的TM10微波，矩形波导右侧封闭，输入微波将在此封闭的矩形波导谐振腔内形成谐振态分布的微波场。在距离输入端244 mm(两倍波长)处设置一同轴波导耦合器(由同轴波导内芯和同轴波导外套组成)。同轴波导耦合器内芯深入至矩形波导内部，与内部谐振电场耦合，将微波电场耦合传输至内芯底部末端。同轴波导外套约束同轴内芯耦合处的微波向底部工件处传输聚焦，但该微波不能远场传输，只会在同轴内芯末端形成的局部微波频率谐振电场。若该谐振电场分布区域穿透工件，则该电场将在工件内部形成有效体加热热源。

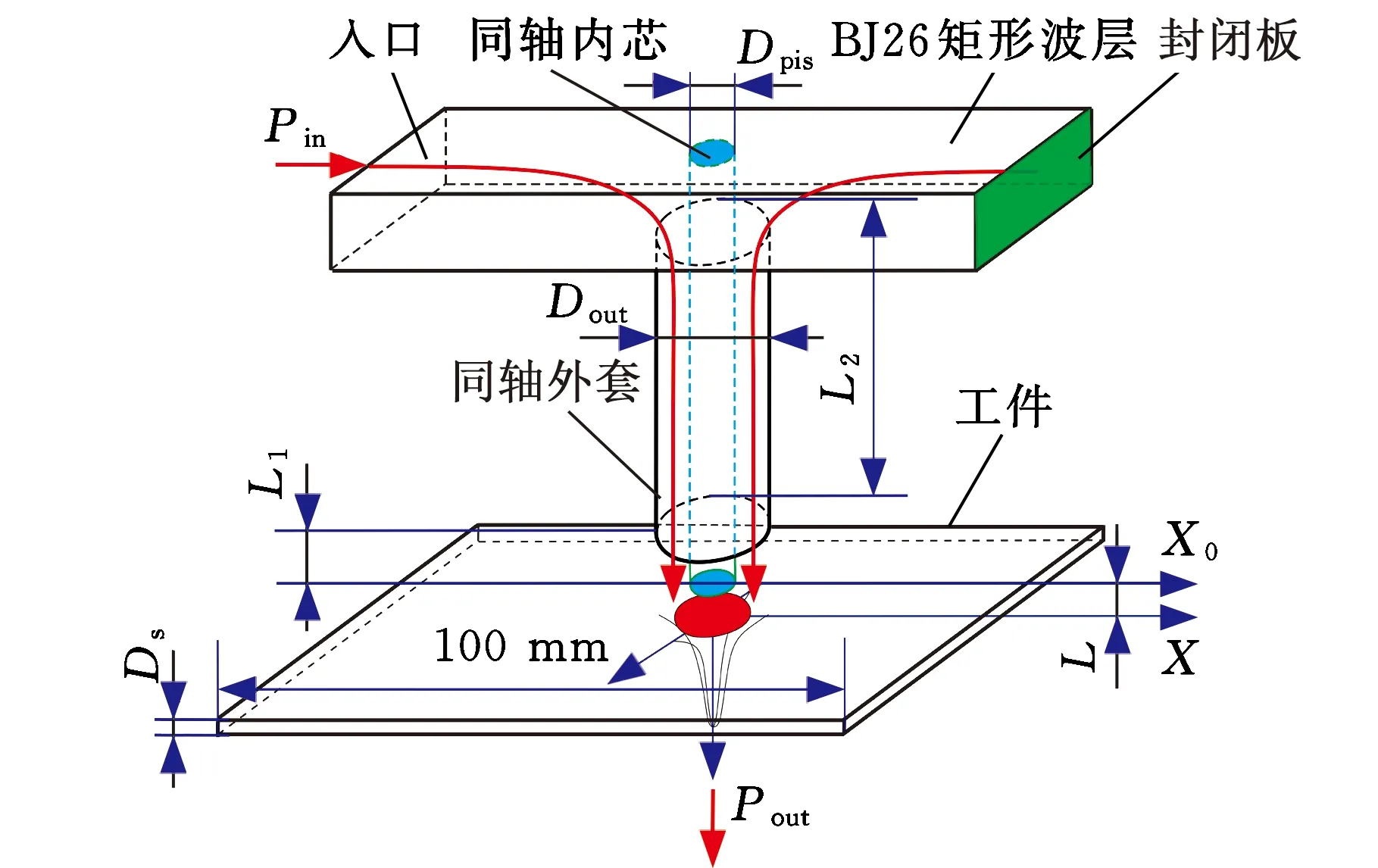
图3 微波热源表征仿真模型Fig.3 Simulating model of microwave heating source

由同轴波导特性可知，影响图3中结构的微波耦合谐振聚焦特性的关键尺寸如下：工件厚度Ds=3 mm、同轴外套直径Dout=70 mm、同轴内芯直径Dpis=10 mm、同轴内芯伸出同轴外套长度L1=5 mm、同轴外套长度L2=220 mm、同轴内芯末端与工件之间距离L=0.5 mm。

微波在传输过程中满足麦克斯韦方程，即

(1)

D=εEB=μH

式中，H为磁场强度，A/m；J为电流密度，A/m2；D为电位移，C/m2；E为电场强度，V/m；B为磁通密度，T；ρ′为电荷密度，C/m3；ε为介电常数，F/m；μ为磁导率，H/m。

将各波导及同轴内芯表面边界条件视为理想导体(PEC)，则微波加热工件时工件区域的电磁场求解问题可转化为在一定的初始条件和边界条件下求解上述微分方程的问题。本文采用电磁仿真软件CST对上述模型中的电磁场分布及热源分布特性进行求解，其中电场强度与热源热功率密度分布之间的关系满足：

Pv=2πfε0ε′tanδ|E|2

(2)

式中，Pv为微波热源热功率密度，W/m3；f为微波频率，Hz；ε0为真空介电常数，ε0=8. 85×10-12F/m；ε′为相对介电常数；tanδ为介电损耗正切；|E|为负载处电场强度幅值，V/m。

将微波作为体加热热源时，工件温度与热功率密度之间的关系满足：

(3)

式中，θ为工件温度，℃；t为加热时间，s；a为吸波材料工件热导率，W/(m·K)；ρ为材料密度，kg/m3；C为材料质量热容，J/(kg·℃)。

热涂层与非吸波脆性材料之间满足传热方程，即

(4)

式中，Q为热流密度(可等效为面热源的热功率密度)，W/m2；z′为涂层厚度，m；a′为等效热导率，W/(m·K)；a1、a2分别为涂层和非吸波材料工件的热导率，W/(m·K)。

依据式(1)～式(4)计算图3所示的微波热源的热功率密度。首先利用CST软件对上述参数下微波电场的谐振特性进行仿真，并计算出聚焦区域微波热源热功率密度分布值；然后利用高斯分布方程对该热源进行拟合，得到考虑各结构参数的微波热源热功率密度拟合方程；接着利用ABAQUS有限元软件和式(3)计算该微波热源热功率密度分布拟合方程作用下的温度场，将该温度场与实际测温结果进行对比，并对该热源热功率密度分布拟合方程的有效性进行验证；最后依据式(4)将石墨涂层的体加热热源转化为工件表面的面加热热源。

基础热源热功率密度仿真分析时工件材质为玻璃，其物理参数见表1，其中相对介电常数和损耗正切值由日本AET公司生产的网络分析仪和共振探针测量得出，其他参数值由玻璃材料厂家提供。

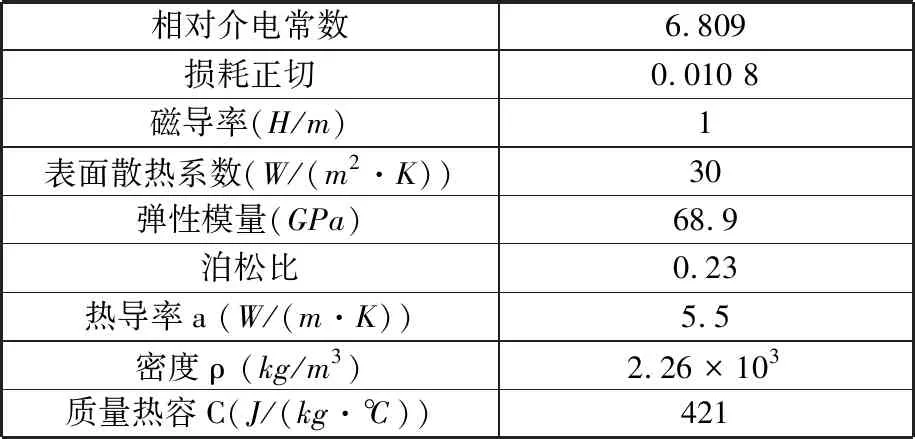
表1 玻璃工件物理参数Tab.1 Physical parameters of glass workpiece

2.2 热源仿真结果拟合

利用满足上述参数的同轴-波导谐振器对尺寸为100 mm×100 mm×3 mm的玻璃工件进行加热，所形成的谐振态微波热源热功率密度的分布云图见图4，其中z为工件内部距工件上表面的距离。微波穿透了玻璃板，对整个厚度的玻璃板均可实现有效的加热，因此该热源为体加热热源。该热源热功率密度等值线为一系列同心圆，可认为该结构实现了圆形分布的谐振态微波热源。该热源与传统激光热源不同，其内部形成的热源值要大于表面形成的热源值，即聚焦微波电场穿透了工件表面，在工件内部形成了更强的聚焦区域。这种热源将在工件内部产生快速加热的效果，更有利于形成热裂法所需的高梯度温度场和应力场。这种内部聚焦生热热源是在热裂法研究中首次被提出，该热源更有利于在较低的温度下诱导初始裂纹扩展，可为降低工件的加工温度和减小残余热应力提供技术保证。

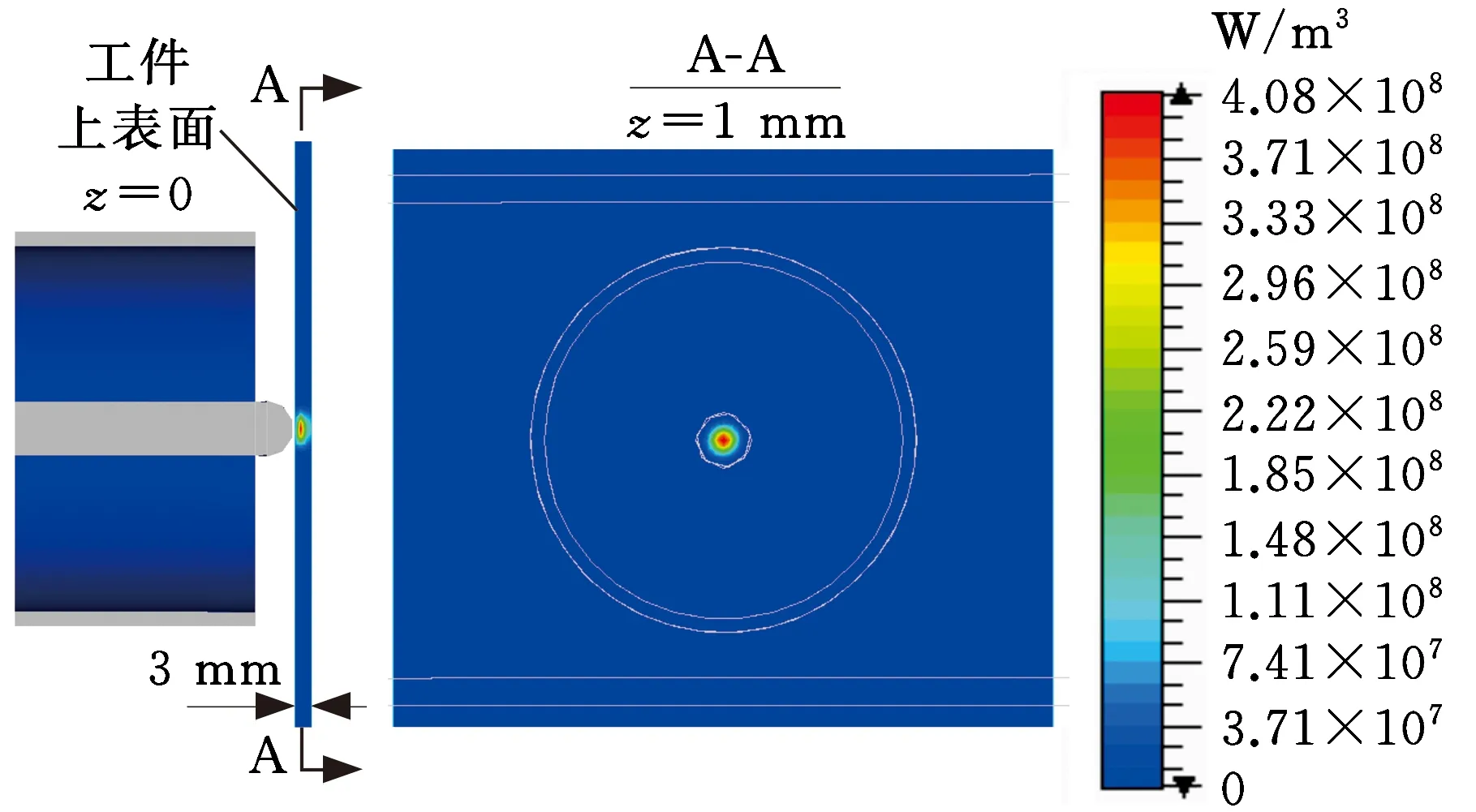
图4 微波热源仿真结果Fig.4 Simulating results of microwave heating source

对工件内部各厚度层的微波热源热功率密度分布进行曲面拟合，可得到工件各厚度层的典型热功率密度分布曲面，见图5。由图5可以看出，微波热源在各层均具有近似的空间分布形式(即均为圆形分布)，热功率密度值在每层的中心点达到最大值。随着厚度的增大，圆形分布的热源直径也在不断增大，工件深层可获得较大的加热区域。已有研究结果表明，加热区域即热压应力区域，该区域越大，越利于形成稳定的裂纹扩展，因此该热源的上述分布特点具有维持裂纹稳定扩展的作用。

观察热源热功率密度分布曲面可以发现，该曲面与高斯曲面具有相似性，因此可考虑利用高斯方程对各层热功率密度分布进行拟合计算，从而可得到各层的热功率密度分布方程。该热源的热功率密度分布拟合方程如下：

(7)

式中，Pv0为热源分层热功率密度，W/m3；P0为高斯拟合方程初值，W/m3；Pv0，max为热源热功率密度峰值，W/m3；Xc、Yc为高斯热源中心点位置坐标值；WX、WY分别为高斯热源降低为热功率密度峰值的e-1倍时等值椭圆X向和Y向的端点坐标值。

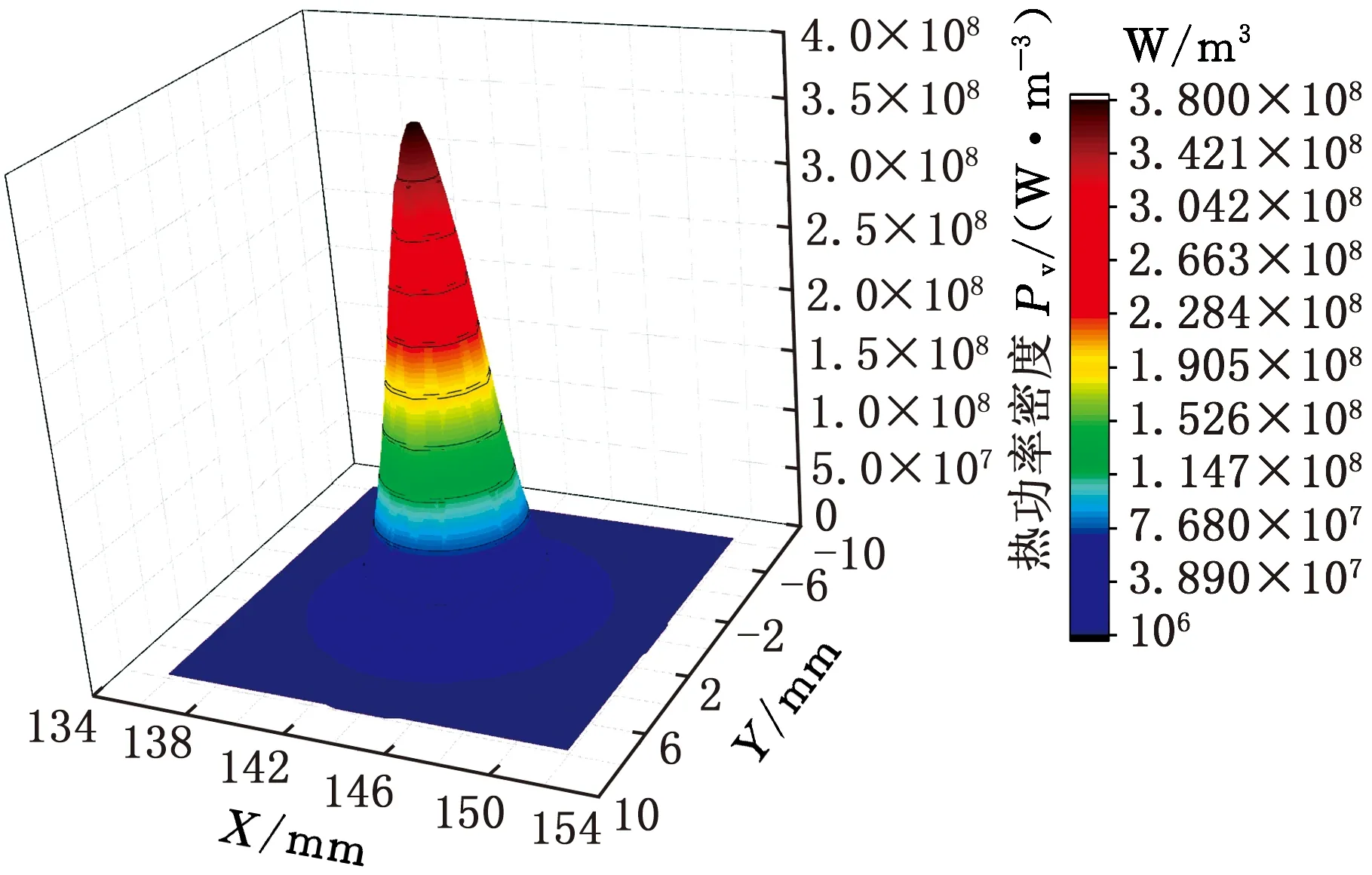
(a)z=0

(b)z=1 mm

(c)z=2 mm

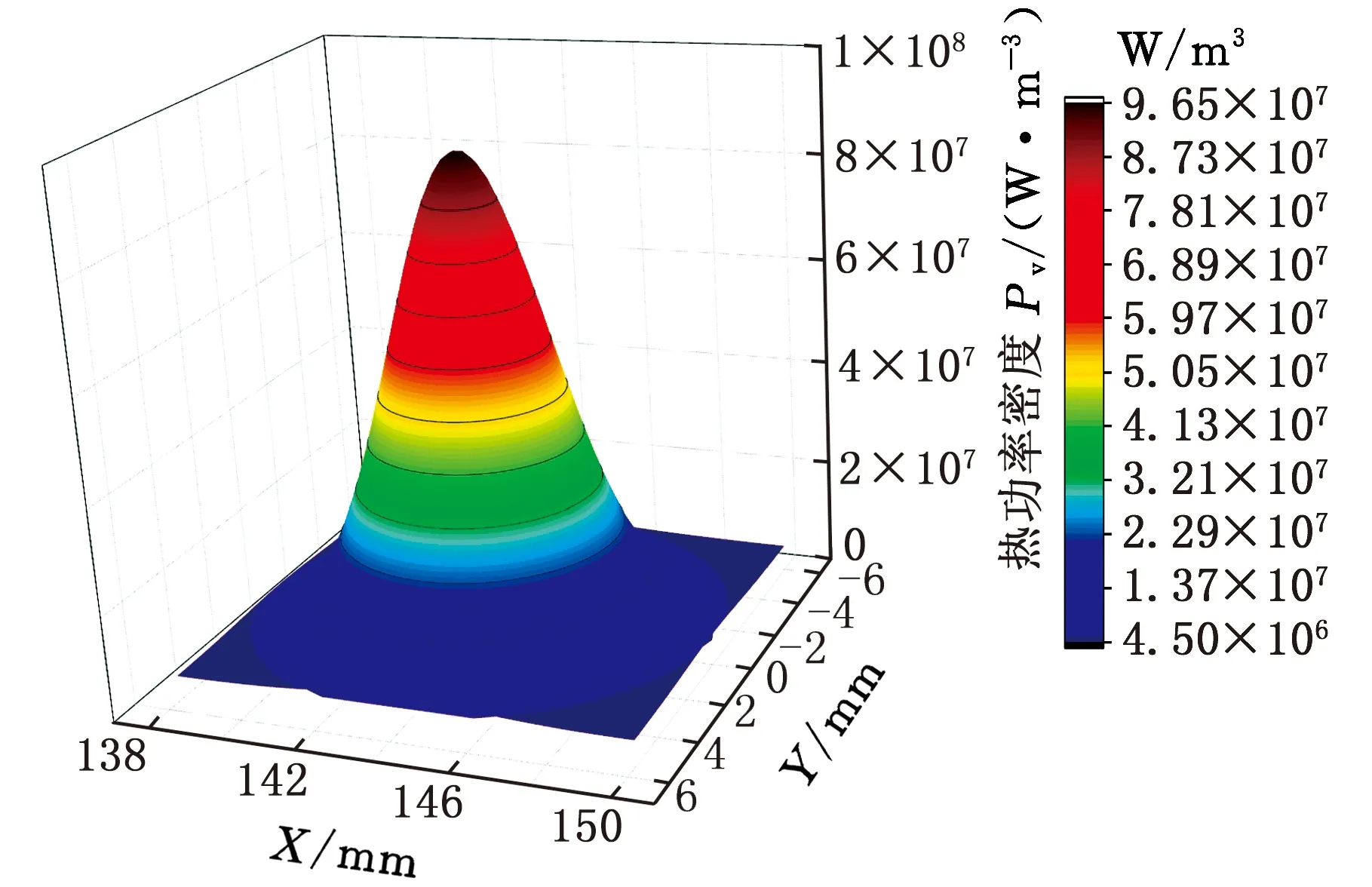
(d)z=3 mm图5 样件厚度层典型微波热源拟合曲面Fig.5 Classical fitting surface of power density of microwave heating source

拟合方程各参数拟合值见表2。由表2可知，各层Pv0,max随厚度z的增大呈现先增大后减小的趋势，在工件内部距工件上表面0.5 mm位置处(即z=0.5 mm时)达到最大值，此处的Pv0,max比表面的Pv0,max增大了3×107W/m3。进一步分析上述拟合方程的参数可以发现，只有高斯分布方程中的Pv0,max、WX和WY对z比较敏感。每层中WX与WY的取值相等，将两者统一为W，且与z近似成线性关系，可得出W与z之间近似满足：

本着体现童真童趣、学生主编的思路，家长可以带领小组同学创编故事，给故事配图。学生创编题材多样，有关爱动物的，有倡导环保的，有书写个人成长的，有改编经典的……每个班都创编、出版一个绘本集，这也是学生上学后自己出的第一本书。

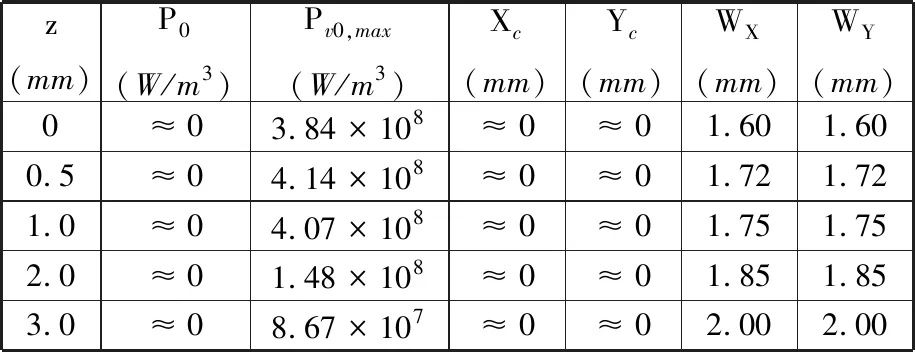
W=1.6+0.13z (8)表2 圆形微波热源热功率密度拟合方程参数Tab.2 Fitting parameters of power densityof circular microwave heat source

根据表2绘制Pv0,max-z曲线，该曲线进一步量化了上述微波热源热功率密度最大值与厚度之间的关系。利用多项式对上述曲线进行拟合，拟合曲线见图6，并得到了用z表示的微波热源热功率密度最大值的表达式：

Pv0,max(z)=(3.801 6+3.206 61z- 3.770 42z2+0.791 5z3)×108

(9)

则整体热源热功率密度Pv2可表示为

(10)

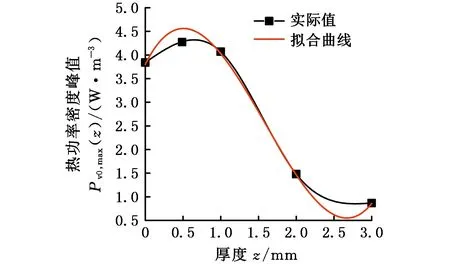
图6 热源热功率密度峰值曲线及拟合方程Fig.6 Fitting curve and equation of the peak of power density of heat source

输入总功率值和工件的介电参数仅影响微波热源热功率密度峰值，而不会改变微波热源热功率密度分布状态。若将1 kW输入功率加热玻璃时所形成的微波热源作为基准，则任意输入功率χ的圆形聚焦微波热源热功率密度Pv3可表示为

Pv3=χPv2

(11)

对于任意介电参数为ε1tanδ1的陶瓷材料，其圆形微波热源热功率密度Pv4可表示为

(12)

2.3 热源表征方程验证

利用功率为1 kW的热源方程仿真分析尺寸为100 mm×100 mm×3 mm的玻璃工件加热过程，工件的温度场分布结果见图7。由图7a可以看出，圆形热源在工件中心加热时，形成了同心圆形的等温区域；在工件内部距工件上表面0.5 mm位置(即z=0.5 mm)处为热源热功率密度最大值处，且由于上下表面存在散热，从而导致工件内部存在较大的高温区域面积。由图7b可以看出，当工件加热70 s时，中心点温度达到了140 ℃左右；随着距离中心点越远，升温速度越慢、温度梯度也越大，这是因为距离中心点越远，微波热功率密度值减小速度越快，微波加热功率与散热功率平衡时所能达到的最高温度也越小，从而导致温度梯度增大。

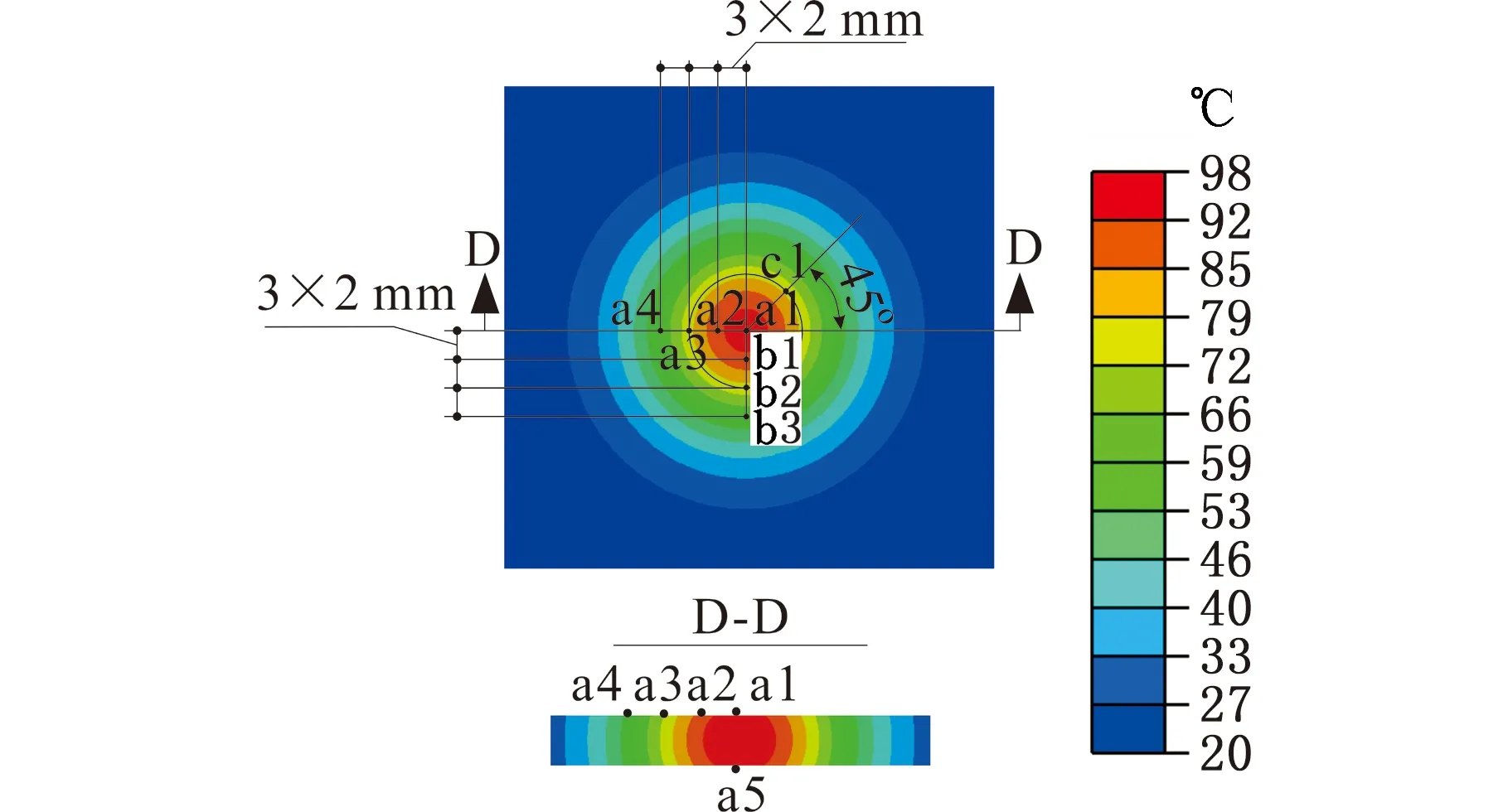
(a)微波加热玻璃过程温度仿真云图

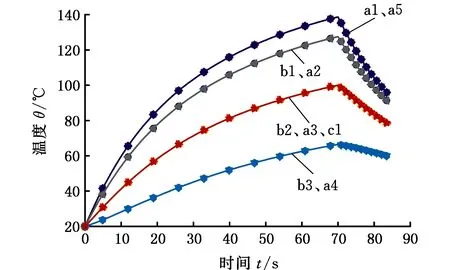
(b)微波加热玻璃样本点温升曲线图7 微波加热温度场仿真结果Fig.7 Simulating results of temperature field heated by microwave heat source

为验证上述仿真结果的正确性，对相同加热过程中实际工件的a1～a5点、b1～b3点以及与a3、b2位于同一个圆上的c1点进行温度测量，测温实验结果见图8。实验结果表明，中心点被该微波椭圆热源加热70 s时，其温度确实达到了140 ℃；在70 s之前，所有点的升温曲线均具有先快速增大后趋于平缓的特征；中心区域的a1点和a5点、b1点和a2点、b2点和a3点与c1点、b3点和a4点的升温曲线的变化趋势分别接近，这说明上述点的热功率密度值接近。距离中心点越远，升温曲线的变化趋势越缓，所能达到的最高温度越小，温度梯度越大。上述结果均与仿真结果具有较好的吻合性，因此可以间接表明仿真计算得出的热功率密度及其拟合方程，可有效地表征微波热源热功率密度分布，利用该热功率密度分布拟合方程仿真分析得出的温度场可有效地表征实际微波热源加热过程中的温度场分布。仿真分析得出的结果是可靠的，过程中误差可控，具有一定的准确性。不同条件下得到的热功率密度分布方程均为上述步骤的重复，具体过程不再累述。

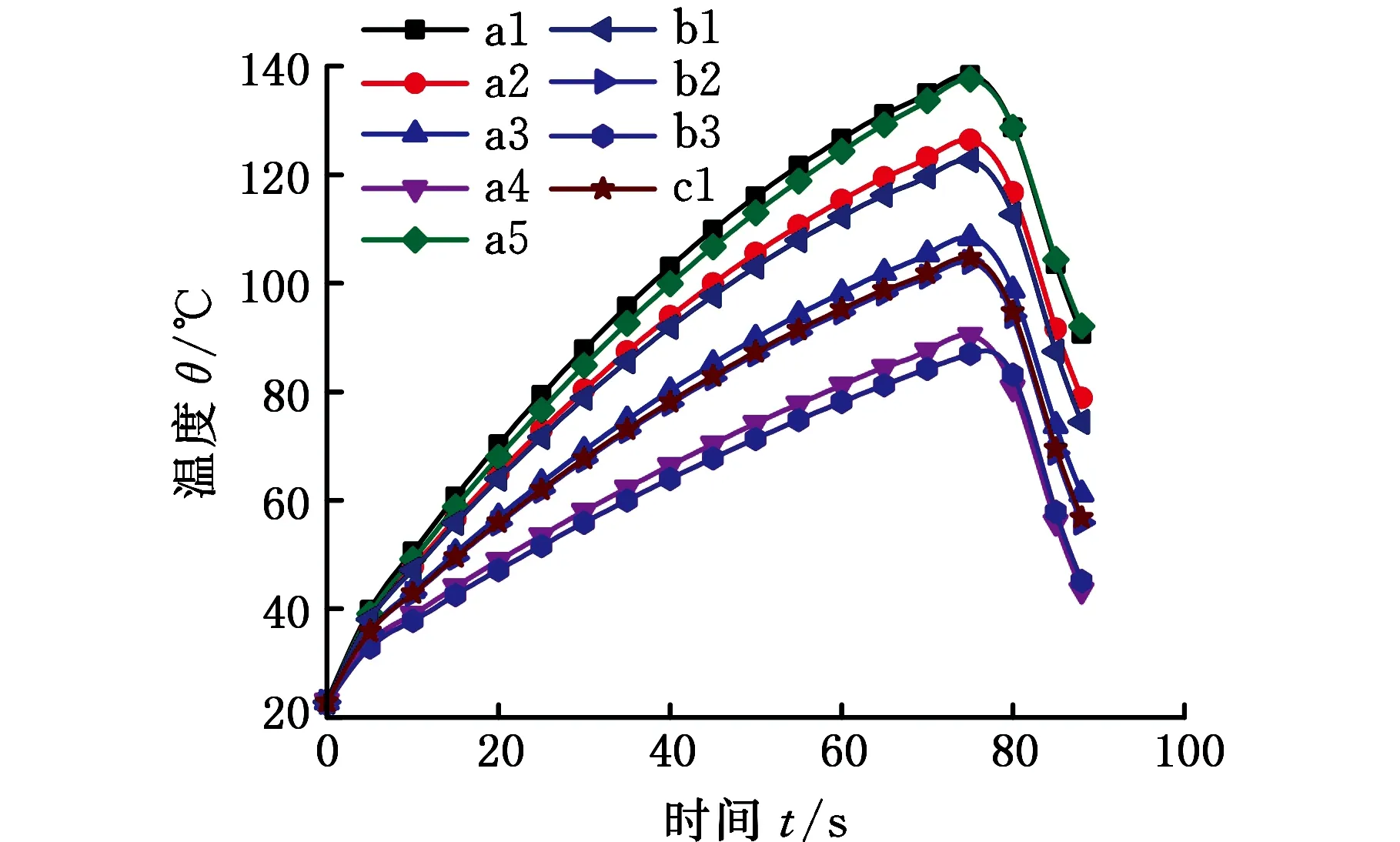
图8 加热区域测温结果Fig.8 Temperature measurement results in the heating zone

3 微波热裂切割陶瓷实验结果

本文成功切割了尺寸均为100 mm×100 mm× 1 mm的氧化锆板和氧化铝板，结果见图9，其中氧化铝陶瓷的切割温度约为260 ℃，氧化锆陶瓷的切割温度约为200 ℃。两种材料的切割轨迹分别见图9a和图9d，可以看出，氧化铝板和氧化锆板的切割轨迹均近似为直线，但在裂纹的起始处，氧化铝和氧化锆切割轨迹均发生了较大的偏移。由图9b可知，表面涂碳层对陶瓷内部具有一定的热扩散渗透的作用，在图9c中可清晰地看到内部碳化的结果。在微波热裂切割过程中，氧化铝陶瓷的涂层表面不时有亮线出现，这是因为有快速的放电产生，快速放电也会使得碳涂层可渗透于材料内部；除了宏观的热应力以外，还有微放电产生的局部热应力，这也是微波能在较低的温度下成功切割氧化铝陶瓷和氧化锆陶瓷的原因(微波切割氧化铝和氧化锆温度均低于300 ℃，而激光切割温度约为1 000 ℃)。对比氧化铝陶瓷和氧化锆陶瓷可以发现，两者初始裂纹处的偏移具有相似性，这与氧化铝和氧化锆在面加热过程中产生的温度场、应力场及裂纹起始处的应力集中因子组成有关。由图9e和图9f可以分析氧化锆陶瓷断面的微观形貌，该断裂是沿晶断裂伴随少数的穿晶断裂，穿晶断裂的一个典型特征就是有较为明显的撕裂面。由观察微观组织可知，氧化锆同氧化铝一样，宏观上具有均匀一致的连续性，但在微观上是不同相的组合，材料内部也充斥着大量的微裂纹和气孔等缺陷，这些缺陷一方面降低了微波热裂切割的温度，另一方面使得裂纹扩展更不稳定，这是利用热控裂纹扩展技术切割陶瓷需要注意的因素。

尺寸均为100 mm×100 mm×3 mm的玻璃和碳化硅板的切割结果见图10，其中玻璃陶瓷的切割温度约为85 ℃、碳化硅陶瓷切割温度约为230 ℃。由图10a和图10d可以看出，碳化硅和玻璃的切割轨迹均为直线，在裂纹的起始处，碳化硅和玻璃切割轨迹发生了不同程度的偏移。在切割过程中发现，碳化硅的裂纹扩展是突变的，即当热源行进至40 mm左右时，碳化硅板突然断裂。这是因为碳化硅板具有较高的导热性，在热源行进至40 mm左右时，在碳化硅板起始裂纹处和末

(a)氧化铝陶瓷切割轨迹 (b)氧化铝陶瓷切割断面 (c)氧化铝陶瓷切割断面(放大图)

(d)氧化锆陶瓷切割轨迹 (e)氧化锆陶瓷切割断面 (f)氧化锆陶瓷切割断面(放大图)图9 微波热裂切割氧化铝和氧化锆结果Fig.9 Thermal controlled fracture results of Al2O3 and ZrO2 by using microwave

(a)碳化硅陶瓷切割轨迹 (b)碳化硅陶瓷切割断面 (c)碳化硅陶瓷切割断面(放大图)

(d)玻璃陶瓷切割轨迹 (e)玻璃陶瓷切割断面 (f)玻璃陶瓷切割断面(放大图)图10 微波热裂切割碳化硅陶瓷和玻璃结果Fig.10 Thermal controlled fracture results of SiC and glass by using microwave

尾均出现了较大的拉应力区，当该拉应力区的应力集中因子超过断裂韧性时，碳化硅板将从两端向中间扩展。碳化硅具有较小的表面能，通过端面分析可以发现，其内部充满了气孔、微裂纹等缺陷(图10b)，这些缺陷导致仅需很小的应变能释放就可实现较大的新端面。此外，碳化硅内部有很多小的碳聚集点，碳的导电性使得该处产生了大量的电荷聚集，极易发生内部打火，形成内部“微爆炸”现象(图10c)，这使得碳化硅陶瓷的断裂极不稳定。与碳化硅不同，玻璃的裂纹扩展是渐进的，即随着热源的扫描过程逐步进行。与激光热裂法相比，微波热裂法可在较低的温度(85 ℃左右)对玻璃实现热控切割。通过分析玻璃的微观组成相(图10e)可以发现，微观尺度的玻璃并非连续一致的均匀相，而是由圆斑型的富硅氧相和聚堆的富钠钙相组成(图10f)，且两者吸收微波的能力并不相同。与富硅氧相相比，富钠钙相具有较大的介电常数和介质损耗系数，因此也具有较高的微波吸收能力。微波加热玻璃的过程，本质上是先加热富钠钙相再将热量传给富硅氧相的过程。两者吸波能力的差距以及两者热导率和热膨胀系数的差距，最终导致产生了不均衡热应力，这种不均衡热应力与宏观的热应力叠加，会导致实际所需要的宏观温度梯度和热应力均小于激光热裂法所需的切割温度梯度和热应力阈值。较低的切割温度意味着较小的残余热应力和较高的切割断面强度，这是体加热微波热裂切割方法的优势。

高能聚焦微波，一方面增加了微波电场强度和利用效率，另一方面不可避免地会产生放电打火现象。当增大微波功率至一定值时，会对所有待加工材料均产生或多或少的放电打火损伤，见图11。微波对玻璃的放电打火会导致玻璃内产生大量的球状缺陷(图11a)，该球状缺陷极不稳定，当不施加任何外力时，该球状缺陷会产生微爆现象，当在此处略微施加外力时，玻璃会炸碎。致密碳化硅内部产生的放电会导致碳化硅局部产生圆形碳化烧黑损伤(图11b)，该损伤降低了裂纹的扩展阈值，使后期的裂纹扩展极不稳定，无法实现有效的热控裂纹扩展切割。由于氧化锆内部存在钇聚集，因此微波在该区域也会产生放电损伤，见图11c，该损伤降低了氧化锆的强度和表面质量，且导致裂纹扩展不稳定。多孔碳化硅内部有大量的石墨聚集区域，该区域也会诱导微波产生聚集放电打火，从而导致出现热损伤，见图11d。由于各种材料引起微波聚集放电打火的机理均不相同，因此微波放电控制无法做到收放自如。这需要对多种材料微波放电机理进行揭示，以此开发微波放电控制技术，减小微波放电对裂纹扩展过程的影响，为热控裂纹扩展切割技术的应用提供有效的技术保障，这也是未来亟需研究的问题。