无人机声学脱靶量测量系统精度分析
2019-12-17吕晓林中国人民解放军92419部队辽宁省兴城市125106
吕晓林/中国人民解放军92419 部队,辽宁省 兴城市 125106
无人机声学脱靶量测量系统声学传感器采用四元十字阵列,可以确定目标在测量坐标系的空间位置。在研究四元十字阵定位算法和精度估计的基础上,采用最佳时延估计法,分析了定位误差产生的原因,推导了误差计算公式,通过仿真计算,四元十字阵天线测距精度受方位角与俯仰角影响较小,测距精度较好,理论上能够满足定位要求。
无人机声学脱靶量测量系统传感器阵列布设方式可分为线型阵列,平面阵列和立体阵列等。线型阵列可确定目标的二维参量;平面阵列能确定目标的三维参量。在时延估计精度相同的情况下,对于不同的阵型,所得到的目标定位性能是不同的。所以在实际应用中,选用和设计合理的阵型是非常重要的。合适的几何阵形,不仅可以消除目标方位变化时对测距精度的影响,还可以抑制时延估计方差对测距性能的影响。
立体阵可以对整个空间进行定位,但其算法要复杂得多。面阵可以在整个平面对目标进行定位,也可以对阵列所在平面为界的半个平面进行定位。由N个声传感器阵元组成的阵列,可以得到N-1个独立的时延,空中的飞行目标对于被动声定位系统来说可以看成点目标,有三个自由度。所以,对目标进行定位,至少需要四个阵元组成的声传感器阵列。
四元十字阵定位算法
四元十字阵传声器阵列由4个微传声器组成如图1所示,T表示目标声源,S1、S2、S3、S4分别表示四个传声器,位于正方形的四个顶点处,用来接收信号。设定S1,为基准传声器,且四个传声器位于同一平面上,设基阵的半径为a,则各个传声器的坐标可表示为:S1(a,0,0), S2(0,a,0), S3(-a,0,0), S4(0,-a,0);声源目标T的位置坐标为(x,y,z),声源T与坐标原点之间的距离为r,仰角为β,方位角为α。
根据图1建立如下方程组:
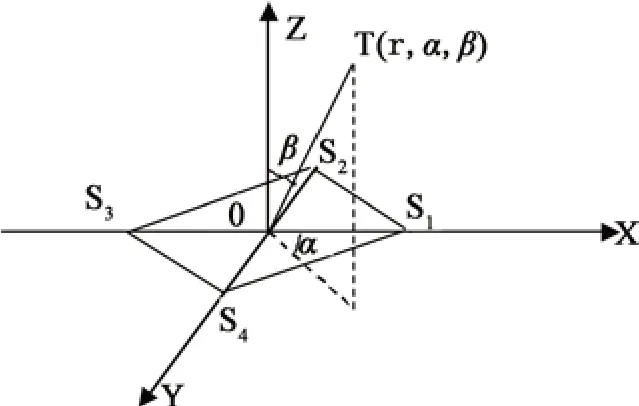
图1 四元十字阵测量示意图

式中,d21,d31,d41分别对应声学传感器与基准声学传感器之间的声音传播路程差。
d21= cτ21,d31= cτ31,d41= cτ41(2)式中:c声速τ21,τ31,τ41分别对应声学传感器与基准声学传感器之间的声音传播路程时延。
直角坐标与极坐标转换关系如下:

解方程组(1),可得:

求解得:

对(4)变换,于是:

由直角坐标与极坐标的关系可以求出方位角α和俯仰角β。

由于r1≫di1,所以

通过上述分析可以看出,只要测量出时延τ21、τ31、τ41,就可以由阵列和目标声源空间几何关系计算出目标发声时的位置,实现对目标定位。
在实际的使用中,将首先采集到目标激波信号的声学传感器定义为基准传感器。相对于基准传感器的激波信号时间差di1取值均大于0。
测量精度分析
为分析问题方便,约定στ为时延误差,σd = cστ为声程误差。
由上式可知,时延值τ21、τ31、τ41,声速c,以及阵元间距a都会对定位精度带来影响。
由于声定位的本质是采用声信号的相位定位,所以各种影响声信号传播,对声定位精度都有直接影响,这些误差通过影响时延估计精度而影响声定位精度,而且各类误差之问是相互独立的,因此,以上各种误差都可以换算为时延误差。
影响声定位的所有误差可以归类为三个方面,即:算法误差,系统误差和随机误差。在此,分别记为στ1、στ2、στ3。
算法误差是由不同时延估计算法带来的,可通过选取高精度的时延估计算法来减小此类误差。
假定信号和噪声是不相关的平稳随机过程,则最佳时延估计误差能够达到Cramer—Rao下限,即,
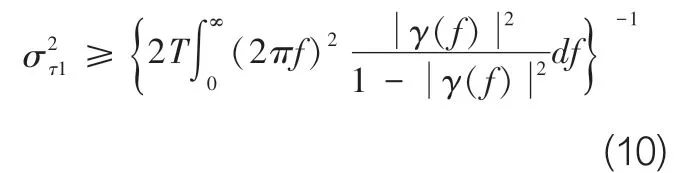
其中,T是观测时间,γ(f)是相关函数,且:
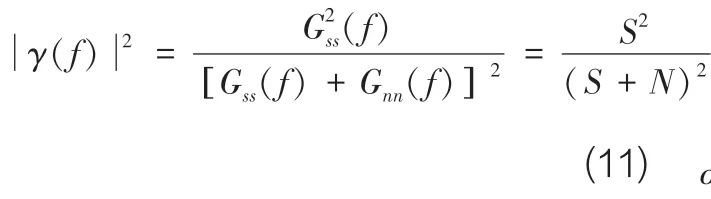
式中,Gss(f)和Gnn(f)分别是噪声和信号的自功率谱,S、N分别代表信号和噪声的功率。假设信号和噪声都是带限白噪声,则,

式中,f1和f2分别是信号处理系统的工作频带的上下限。
从上式可知,算法误差与信噪比、观测时间、工作频带有关,结合声测系统实际工作环境,一般情况下取στ1=2~8μs。
系统误差主要由阵元间距误差即测量系统电气性能不一致产生的,声接收传感器的时延误差στ2=9~15.8μs 。
随机误差主要由信号传播起伏及风的影响带来的声信号的幅度和相位起伏所致,其中,相位起伏为主要影响因素。一般情况下,取随机误差στ3=13.13~20.7μs 。
由于以上所述各类误差之间是不相关的,而各通道的时延误差的统计误差特征也是相同的,所以,各类误差折合的时延误差用στ表示,由误差合成理论,总的时延误差可表示为:
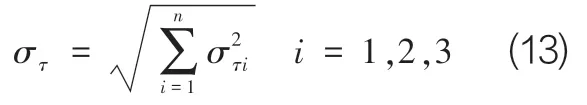
将στ1、στ2、στ3带入上式,可得
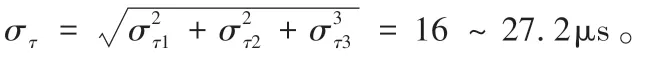
对平面四元十字阵定位误差,为了使分析结果更具有普遍意义,统一采用误差合成理论来推导时延估计误差所带来的方位角、俯仰角以及距离估计误差。
方位角估计精度分析
根据误差合成理论,方位角的误差可表示如下:

最终可得,

俯仰角估计精度分析
根据误差合成理论,俯仰角的误差可表示如下,

由时延估计误差引起的俯仰角误差为:
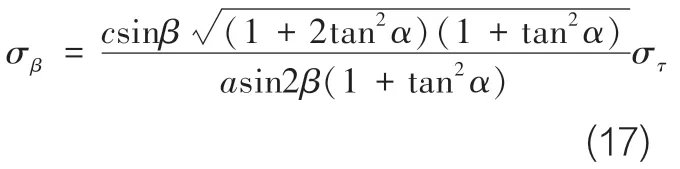
距离估计精度分析
根据定位原理和极坐标转化关系来分析声阵列的距离估计精度,根据误差合成理论,可获得距离估计误差的表达式如下,

依据误差合成理论,可分别得到x、y、z的误差表达式如下,
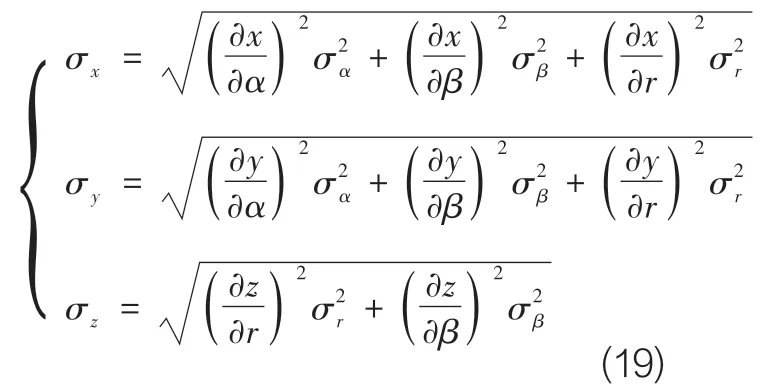
经化简整理可得:
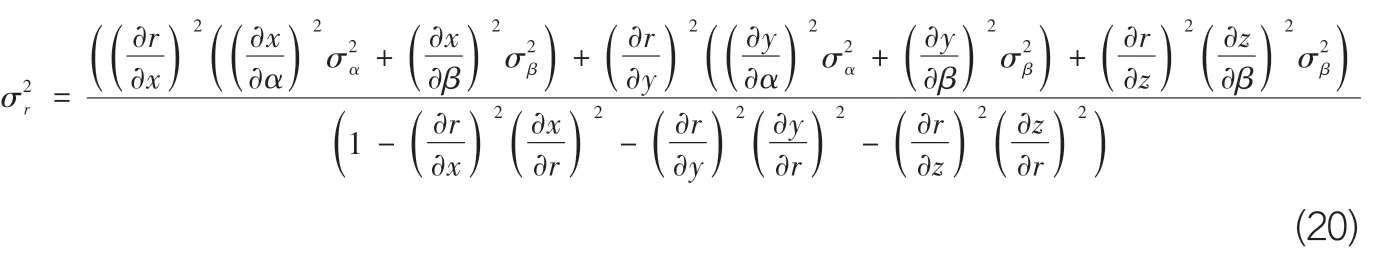
仿真计算
采用MATLAB对平面四元十字阵的定位精度进行了仿真,仿真分别从方位角、俯仰角和距离估计精度三个方面进行。
方位角估计精度仿真
图2和图3分别是方位角误差与方位角、俯仰角的关系图(俯仰角为60°、方位角为60°、阵元间距为0.95m、声速为340m/s)。
由图2可以看出,方位角的改变对方位角估计精度影响不大。
由图3可知,方位角误差随俯仰角的减小呈逐渐增大的趋势。但这种改变十分缓慢,所以在绝大部分的俯仰角范围内,可以认为方位角误差不受俯仰角的影响。但当俯仰角小到一定程度后,方位角误差开始明显增加,而当俯仰角接近于零时,误差激增。此时阵列已失去定向能力,但实际上,此时目标正处于阵列正上方,已没有必要再精确地判定方位角了。

图2 方位角误差与方位角关系图

图3 方位角误差与俯仰角关系图
由仿真结果可知,在时延估计达到一定精度后,在相当大的角度范围内,方位角的估计误差都在0.6°以内,所以,平面四元十字阵对方位角的估计稳定性与精确度都是较好的,仿真结果表明其能够满足实际定向的要求。
俯仰角估计精度仿真
图4和图5分别是俯仰角误差分别与方位角、俯仰角的关系图。
由图4可以看出,由方位角的改变引起的俯仰角误差的波动较为平缓,方位角的改变对俯仰角估计精度影响不大。

图4 俯仰角误差与方位角关系图
由图5可以看出,俯仰角误差受俯仰角影响较大,俯仰角误差在俯仰角接近90°时急剧增加,所以,俯仰角接近90°的区间是平面四元十字阵的俯仰角定位盲区,但考虑到这种情况一般出现在目标处于远场,其带来的实际影响相对较小。
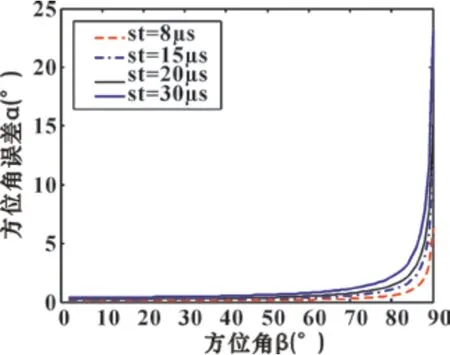
图5 俯仰角误差与俯仰角关系图
从仿真结果来看,平面四元十字阵俯仰角判定精度较好,定向盲区带来的实际影响较小,所以能够满足定向测量要求。
距离估计精度仿真
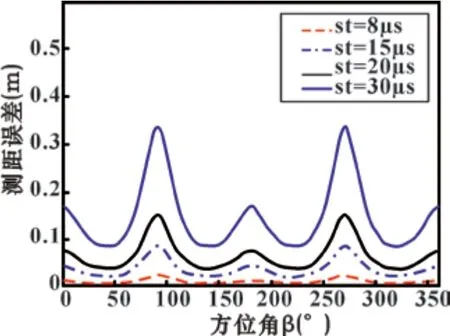
图6 测距误差与方位角关系图
图6和图7分别是测距误差与方位角、俯仰角的关系图(距离取50m)。
由图6可知,相比绝对误差,测距误差随方位角不同而变化的改变值较小。所以,整体上仍可以认为测距精度受方位角影响较小。

图7 测距误差与俯仰角关系图
由图7可知,测距误差基本上是随俯仰角的减小而增大。由以上两图可以看出,距离误差受方位角和俯仰角的影响都较小。
图8是测距误差与目标距离的关系图。可以看出,测距误差与目标距离呈正比关系。当目标在50m以内时,测距误差小于1m。
结论
综上所述,以上仿真结果表明,无人机声学脱靶量测量系统测距精度受方位角与俯仰角影响都较小,测距精度较好,理论上能够满足定位要求。

图8 测距误差与目标距离关系图
