基于熵值法和比较静态分析的省级农业科技DEA效率

董奋义　齐冰

摘要：我国正处在传统农业向现代农业转型的关键时期，而科技是农业快速发展的重要手段。基于熵值法计算出我国各省份农业科技发展程度与相对农业科技产出，并利用数据包络分析（DEA）模型对我国2005、2010、2015年各省份的农业科技DEA效率进行比较静态分析。结果表明：我国多数省份的农业科技DEA效率处于非DEA有效状态，2005—2015年我国整体农业科技水平呈下降趋势;大部分省份农业科技DEA效率处于无效状态，这是因为纯技术效率与规模效率的发展存在严重失衡。最后，根据分析结果提出了相关对策建议。

关键词：农业科技;熵值法;DEA模型;技术效率;规模效率;比较静态分析;对策建议

中图分类号： F302文献标志码： A

文章编号：1002-1302（2019）19-0321-06

收稿日期：2018-07-16

基金项目：国家自然科学基金（编号：41171444）;河南省软科学项目（编号：182400410256）;河南省高等学校重点科研项目（编号：15A630032）。

作者简介：董奋义（1972—），男，河南平舆人，博士，副教授，从事灰色系统理论、决策分析等研究。E-mail：dfenyi@163.com。

“民以食为天。”粮食的重要性奠定了农业在我国的基础地位，我国作为世界人口第一大国，农业的发展对我国的重要性不言而喻。农业的发展来源于工业发展的反哺，可以说农业的发展取决于人类科技的整体进步。众所周知，虽然中国正处于传统农业向现代农业转型时期，但不可否认，中国农业科技水平落后于发达国家。因此，对我国农业科技效率进行评价，不仅有利于我国农业从事者发现自身的差距与不足，而且对于其更合理地进行科技资源配置、提升科技资源的使用效率、加速农业转型有着现实的意义。

很多学者都对农业科技投入所产生的影响进行了研究与分析。孙慧波等利用DEA-Tobit两步法对全国农业科技服务对农业生产效率的影响进行了实证分析[1]。杨剑波利用协整分析方法、向量误差修正模型等证明农业科技投入的变化会导致粮食产量的重大变化[2]。张红辉等采用分布滞后模型等方法证明了农业科技投入与农业经济增长之间存在长期的稳定均衡关系[3]。黄敬前等也利用协整理论与方法分析了我国农业科技投入与农业科技进步之间长期的均衡关系[4]。刘敦虎等利用动态计量分析模型研究四川省农业科技投入与农业经济增长的动态关系，证明了四川省农业科技投入对其农业经济增长具有重要作用[5]。除此之外，还有很多学者研究了农业科技投入对于农业生产[6-10]、农业科技投入效率[11-15]等的影响。但是大多数学者在进行研究时只是把我国农业科技作为一个整体，单纯地对我国或者各省份进行农业科技投入效率测算与分析，并没有对我国各省份的农业科技水平提供一个定量研究，且农业科技投入产出指标大多还不具有一致性，如研究农业科技的科技论文数却使用各行业整体的科技论文数来代替等。可见，运用上述内容测算得出来的结果对于清晰地认识我国各省份农业科技水平的意义是有限的。

因此，本试验基于以往学者的研究，以熵值法为工具，以各省份的农业科技相关数据为基础，在对我国各省份农业科技水平与农业科技产出进行定量研究的基础上，利用DEA模型对我国2005、2010、2015年各省份的农业科技DEA效率进行比较静态分析。最后，在对2005、2010、2015年我国各省份农业科技DEA效率进行分析的基础上，提出相应的对策建议。

1 模型介绍

1.1 农业科技产出测算方法

各省份农业科技发展水平的测算是一个复杂的过程，只有正确得出农业科技发展水平，才能得出具有可信度的农业科技产出。为保证计算得出的农业科技发展水平具有客观性与可信度，筆者借鉴文献[16-19]，采用熵值法作为计算农业科技发展水平的工具。熵值法是根据各指标的变异程度利用信息熵计算各指标的熵值，能深刻反映出指标的区分能力的一种客观赋权方法。相对于主观赋权法，熵值法具有较高的可信度和精确度。因此，利用熵值法可以把各项农业科技产出指标作为一个整体对各省份进行客观的衡量，以大致得出各省份的农业科技发展水平。设有m个评价对象、n个评价指标，原始评价对象的指标值可以用矩阵X=（xij）mn来表示。具体计算步骤如下：

（1）由于在评价指标体系中各指标在量纲等方面可能存在较大差异，应对指标进行标准化处理。

正向指标：xij′=xij-min（xij）max（xij）-min（xij）;

逆向指标：xij′=max（xij）-xijmax（xij）-min（xij）。

可以得到标准化矩阵X=（xij′）mn，为方便起见，标准化后的数据仍记为X=（xij）mn。

（2）计算第j项指标下第i个评价对象的指标值的比重pij。

pij=xij∑mi=1xij。（1）

（3）计算第j项指标的熵值ej与信息冗余程度dj。

ej=-k∑mi=1pijln（pij），dj=1-ej。（2）

式中：k=1lnm，1lnm≥0，若pij=0，则定义limpij→0pijlnpij=0。

（4）进而确定各指标的权重wj。

wj=dj∑nj=1dj。（3）

（5）计算各评价对象的综合得分si，si也是本试验所求的各省份的农业科技发展水平。

si=∑mi=1wjxij′。（4）

式中：si∈（0，1），是各省份对农业科技重视程度与发展水平的体现，si越大，表示其所在城市的农业科技发展水平越高。

（6）通过综合得分si折算出理论上我国各省份相对农业科技产出Oi。具体折算方法如下

Oi=si×zi。（5）

式中：zi为农林牧渔总产值，表示在农林牧渔总产值中农业科技所产生的经济效益，即相对农业科技产出。各省份农业科技发展程度不同，农林牧渔总产值水平不同，甚至相差数倍，因此各省份得出的相对农业科技产出也会不同，甚至相差数倍。

1.2 技术效率测算方法

关于效率的评价方法，包括以随机前沿分析法（SFA）、自由分布法（DFA）为代表的参数法与以数据包络分析（data envelopment analysis，DEA）为代表的非参数法等，考虑到农业科技各指标的关系可能适用于不同的函数形式，且参数法的赋值方法带有主观性，故采用非参数法中的数据包络分析作为本研究的技术效率测算模型。DEA模型是美国著名运筹学家Charnes、Cooper和Rhodes于1978年正式提出的以相对效率概念为基础，以凸分析和线性规划为工具，计算比较具有相同类型的多投入、多产出的决策单元（decision making unit，DMU）之间的相对效率，并对评价对象作出评价的方法[20]。其基本模型为C2R模型与BC2模型，两者之间区别在于C2R模型假定规模报酬不变（CRS），BC2假定规模报酬可变（VRS），其中BC2模型更符合农业科技投入与产出的情况。因此，本研究计算模型选用BC2模型。

假设n个决策单元对应的输入数据xij（i=1，2，…，m）和输出数据yrj（r=1，2，…，s），vi为对第i种输入数据的权重，ur为对第r种输出数据的权重，则xj=（x1j，x2j，…，xmj）T，yj=（y1j，y2j，…，yrj）T，v=（v1，v2，…，vm）T，u=（u1，u2，…，us）T，其中，xj>0，yj>0，j=1，2，…，n，描述了第j个DMU的投入和产出情况。

则投入导向角度的线性规划BC2模型（本研究所用模型均为投入导向）为：

（PIBC2）max （μTy0+μ0）=VP

ωTxj-μTyj-μ0≥0，j=1，2，…，n

ωTx0=1

ω≥0，μ≥0。（6）

其中：VP为最优效率评价指数;ω=tv，μ=tu，其中t=1[]vTx0，u、v为权重向量;对j0个决策单元进行效率指标评价时，为方便起见，记（x0，y0）=（xj0，yj0）。

为了更方便对BC2模型进行求解，引入非阿基米德无穷小量ε与松弛变量s-、s+的对偶BC2优化模型，表示为：

（DIε）min[θ-ε（e^Ts-+eTs+）]

∑nj=1xjλj+s-=θx0

∑nj=1yjλj-s+=y0

∑nj=1λj=1

s-≥0，s+≥0，λj≥0，j=1，2，…，n。（7）

式中：e^T=（1，1，…，1）Em，eT=（1，1，…，1）Es。θ为被评价DMUj0的有效值，即效率值;λ是相对于DMUj0重新构造一个有效的DMU中n个决策组合单元的组合比例。

则对偶规划（DIε）最优解为λ0、s-0、s+0、θ0：（1）若θ0<1，则DMUj0不为弱DEA有效（BC2）;（2）若θ0=1，e^Ts-0+eTs+0>0，则DMUj0仅为弱DEA有效（BC2）;（3）若θ0=1，e^Ts-0+eTs+0=0，则DMUj0为DEA有效（BC2）。

2 省级农业科技发展水平及DEA效率测算

2.1 省级农业科技产出测算

农业科技发展主要来源于农业研究和开发机构与高等院校，鉴于高等院校的农业科技研究相对于研究与开发机构的农业科技研究对农业发展的影响较为滞后，因此，本研究所有农业相关数据为农业研究发展机构数据。对于我国各省份（不含香港、澳门、台湾;西藏数据缺失，亦不包含）农业科技产出测算，遵循选取数据的可获取性、连贯性、综合性、客观性、代表性等原则，参考已有研究，以农业科技水平作为一级指标，选取研究与开发机构人员（人）、研究与开发机构内部经费支出（万元）、技术市场成交额（万元）、科技论文数（篇）（以上指标均为农业方面）作為二级指标。本研究所选取的农业科技指标体系包含一个地区从资金、人员投入到直接产出、间接产出，清楚完整地表达了一个地区的农业科技水平。本研究所采用的指标数据均来自《中国统计年鉴》《中国科技统计年鉴》《中国农村统计年鉴》以及各地方统计年鉴。在数据搜集过程中，我国农业科技的数据不仅不完整且有些地区数据多年不变，这在现实经济活动中是不可能存在的，因此为了更好地反映出各地区农业科技发展水平、了解各地区农业科技发展状况，本研究所用数据已事先经过整理处理，处理方法为：对于各省份缺失的数据，均采用灰色系统理论中的 GM（1，1） 预测模型对数据进行补齐;有些省份数据大量缺失且无法采用灰色GM（1，1）预测模型补齐的，采用数据折算方法进行整理，即搜集所有行业同类型的总数据作为原始数据，对农业方面数据进行折算，某年折算数据=某年所有行业同类型总数据×（某年农林牧渔总产值/某年国民生产总值）。鉴于篇幅，原始数据不再给出。

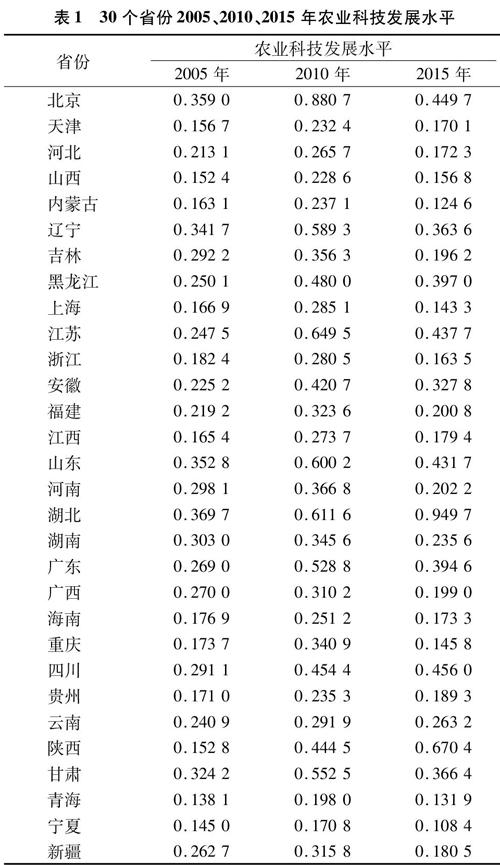
通过对各指标进行标准化，计算评价对象指标值的比重pij、各指标的熵值ej与信息冗余程度dj，并确定各指标的权重wj与各评价对象的综合得分si，即各省份的农业科技发展水平，结果见表1。

农业科技发展水平越高，表明本地区的农业科技水平越高。根据30个省份的农业科技发展水平，可以得到理论上各省份的相对农业科技产出Oi，结果见表2。

从表1、表2中可以看出，科技实力雄厚的地区，如北京、江苏等，科技发展水平较高，由于产业结构侧重不同，农业科技产出与农业科技发展水平的排名并不一致。须要说明的是，各省份的农业科技发展水平是根据各个指标客观权重计算得出的各省份的农业科技发展各指标的综合得分，表1只代表各省份相对农业科技发展程度，而表2依据各省份的农业科技发展水平计算得出相对农业科技产出，其差距较大，主要有以下2点原因：第一，各省份的农林牧渔总产值参差不齐，农林牧渔总产值最高与最低的省份相差数倍;第二，我国各省份农业科技发展程度差距较大，且两极分化比较严重。表2的农业科技产出只是根据熵值法求出的农业科技发展程度得到相对科技产出理论值，主要服务于各省份农业科技投入DEA效率测度，各省份相对农业科技产出的大小只是相对意义上的，并无特殊含义。

4 结语

本研究通过熵值法计算出各省份的农业科技发展水平与相对农业科技产出，运用DEA模型测算DEA效率，并对我国各省份在2005、2010、2015年的DEA效率进行比较静态分析，得出如下结论：第一，我国大部分省份农业科技DEA效率是非DEA有效的，绝大部分省份受技术无效和规模无效的双重作用，且2005—2015年我国农业科技水平整体上呈下降趋势。第二，在部分省份农业科技水平发展过程中，增强规模效率、提高规模报酬是使其转变为DEA有效的最佳途径。第三，大部分省份特别是偏远地区，纯技术效率的提高是其农业科技DEA效率提高的关键因素。第四，大部分省份纯技术效率与规模效率发展严重失衡，导致其综合效率低的原因是其中一方面发展良好，而另一方面发展落后。

因此，提高我国各省份农业科技水平主要应在以下几个方面进行调整：（1）继续深化农业科技研究，努力促进农业科技成果转化。中国正处于传统农业向现代农业转型的关键时期，构建现代农业科技创新体系是实现我国农业现代化和农业经济持续增长的重要战略支撑[21]，因此，我国要继续加大对农业科研的支持力度，对农业科技方面提供政策支持，培养专门的农业科研与技术人才。然而，现阶段我国农业科研过于看重学术价值，忽视其应用价值及推广价值，从而导致我国农业科技成果转化率较低。所以，我国各省份不仅要继续深化农业科技研究，更要努力促进农业科技成果的转化，以便更好地服务于我国农业现代化。（2）调整优化农业科技资源投入结构，增强规模优势。相对于美国等农业发达国家实行大规模现代化作业，我国多数地区农业分布相对分散，虽然各省份整体上规模效率良好，但我国农业的发展并不具有规模优势。因此，在我国大部分非DEA有效的省份要在努力提高技术效率的同时，完善农业科技管理体制，大力宣传规模经济的优势，促进农业合作社等农业集约化生产方式的发展，以促进机械化程度的提高。并在此基础上，有步骤地继续支持农业适度扩大规模经营，对农业科技资源结构进行调整优化，提高增强规模优势、规模效益。（3）深刻剖析导致农业科技非DEA有效的原因，合理配置农业科技资源。导致各省份之间农业科技DEA效率非DEA有效的原因不尽相同，因此，对于非DEA有效的省份应该深入剖析其无效的根本原因，不能只盲目地增加农业科技投入，各省份不能盲目增加农业科技资源投入，应找出导致各省份综合效率低下的根源，进而有针对性地采取措施，力求全面提升农业科技水平。（4）着重建设农业科技水平落后地区，全面提高我国农业科技水平。我国幅员辽阔，区域间自然要素禀赋与农业发展水平差距甚大。各省份间农业科技水平发展程度的不一致，导致整体上我国农业科技发展水平的低下。而各省份间农业科技发展水平的巨大差距是导致我国30个省份综合效率平均值落后的主要原因。因此，增强我国农业科技整体实力，需要国家对农业科技发展水平落后地区进行重点扶持，以缩小各省份农业科技DEA效率之间的差距。

须要提出的是，本研究所测算出来的农业科技DEA效率相对于其他学者的研究结果来说偏低，因为本试验运用研究与发展机构中关于农业科技的数据，利用熵值法计算农业科技产出，构建的投入指标与产出指标之间更具有一致性。

参考文献：

[1]孙慧波，赵 霞，何晨曦. 农业科技服务对农业生产效率的影响研究[J]. 科技管理研究，2016，36（12）：256-260，266.

[2]杨剑波. 1978—2003年我国农业科技投入和粮食产量关系的计量分析[J]. 科技管理研究，2007（5）：69-71.

[3]张红辉，李 伟. 农业科技投入与农业经济发展的动态关联机制分析[J]. 科技管理研究，2013，33（11）：149-151，159.

[4]黄敬前，郑庆昌. 我国农业科技投入与农业科技进步长期均衡关系研究[J]. 福州大学学报（哲学社会科学版），2013，27（3）：48-51.

[5]刘敦虎，赖廷谦，王 卿. 农业科技投入与农业经济增长的动态关联关系研究——基于四川省2000—2015年的经验数据[J]. 农村经济，2017（10）：118-122.

[6]罗小锋. 农户对生产中科技作用的认知及影响因素分析——基于9省1 311户农户的调查[J]. 农业技术经济，2010（8）：80-86.

[7]宋德军. 中国农业产业结构优化与科技创新耦合性评价[J]. 科学学研究，2013，31（2）：191-200.

[8]尹朝静，李谷成，范丽霞，等. 气候变化、科技存量与农业生产率增长[J]. 中国农村经济，2016（5）：16-28.

[9]金怀玉，菅利荣，焦立新. 安徽省农业技术效率变动的实证分析[J]. 中国科技论坛，2011（7）：129-133，146.

[10]杜 娟. 基于DEA模型的我国农业科技创新投入产出分析[J]. 科技进步与对策，2013，30（8）：82-85.

[11]杜宇能，潘驰宇，宋淑芳. 中国分地区农业现代化发展程度评价——基于各省份农业统计数据[J]. 农业技术经济，2018（3）：79-89.

[12]丁 雪，潘晨晔. 基于DEA模型的我国主要省市农业科技投入产出效率分析[J]. 现代农业科技，2015（3）：319-320.

[13]杨印生，王 舒，王海娜. 基于动态DEA的东北地区玉米生产环境效率评价研究[J]. 农业技术经济，2016（8）：58-71.

[14]李子君. 基于DEA的辽宁省农业生产效率分析[J]. 农业经济，2018（2）：54-56.

[15]许云芳. 基于DEA模型的山西省农业资源利用效率研究[J]. 山西农业大学学报（社会科学版），2018，17（4）：55-61

[16]黄安胜，许佳贤，刘振滨，等. 中国绿色农业技术效率及其省际差异分析——基于1998—2012年的面板数据[J]. 湖南农业大学学报（社會科学版），2014，15（4）：68-75.

[17]杨 丽，孙之淳. 基于熵值法的西部新型城镇化发展水平测评[J]. 经济问题，2015（3）：115-119.

[18]杨 龙，胡晓珍. 基于DEA的中国绿色经济效率地区差异与收敛分析[J]. 经济学家，2010（2）：46-54.

[19]辛 岭，高睿璞. 我国新型农业经营体系发展水平评价[J]. 经济学家，2017（9）：73-80.

[20]Charnes A，Cooper W W，Rhodes E. Measuring the efficiency of decision making units[J]. European journal of operational research，1978，2（6）：429-444.

[21]王雅鹏，吕 明，范俊楠，等. 我国现代农业科技创新体系构建：特征、现实困境与优化路径[J]. 农业现代化研究，2015，36（2）：161-167.