要素市场扭曲对区域创新效率的影响研究

2019-12-16郭将肖慧

科技与管理 2019年5期

郭将　肖慧

摘要：对劳动力要素市场扭曲和资本要素市场扭曲进行理论分析与假设，在运用随机前沿法测算区域创新效率的基础上，引入空间计量模型，研究发现考察期间我国劳动力和资本要素市场扭曲对区域创新效率整体呈抑制作用，但要素市场的抑制作用呈现地区异质性，劳动力市场扭曲对西部的抑制作用更强，而资本市场扭曲则对东部地区创新效率的负面影响更显著。

关键词：要素市场扭曲;区域创新效率;异质性;空间相关

DOI：10.16315/j.stm.2019.05.002

中图分类号： F0615

文献标志码： A

Research on the influence of factor market distortion on

the regional innovation efficiency

GUO Jiang， XIAO Hui

（Business School， University of Shanghai for Science and Technology， Shanghai 200093， China）

Abstract：This article mainly uses labor and capital market distortions for theoretical analysis and hypothesis， introducing the spatial econometric model on the basis of the measurement of efficiency of regional innovation by applying stochastic frontier. The study shows that during the observation period labor and capital market distortions inhibit the regional innovation efficiency on the whole， but the inhibitory effect presents the regional heterogeneity， labor market distortions has stronger inhibitory effect on the western region， while the negative effect of the capital market distortions in the eastern is more significant.

Keywords：factormarket distortion; regional innovation efficiency; heterogeneity; spatial correlation

收稿日期： 2019-06-29

作者简介：郭将（1978—），男，副教授，博士;

肖慧（1993—），女，碩士研究生.

改革开放40年来，我国依靠资源的大量投入，总量上经济已跃居世界第二，但质量上我国还处在全球价值链的中低端，缺乏核心竞争优势。而当前，我国经济更是面临着内忧外患的局面。国内消费和投资均面临着下行压力，国际上美国为维持自身技术优势，有意遏制中国产业升级和出口。中国经济要想维持增长并摆脱受制于人的困境势必要充分利用并调动好各个生产要素，提高自主创新能力。

回顾我国的经济发展历程，在早期依靠有形要素的成本优势，经济增速得以加快。但这种粗放式的经济增长方式所导致的资源消耗和污染等诸多弊端正逐渐放大，其中很重要的一点就是创新低效，如何改善资源配置以促进创新效率的提高已成为一个亟待解决的问题。传统经济学一般认为，在完全竞争市场条件下，企业会按照要素价格等于边际产出的原则安排生产，达到帕累托最优状态，但现实是我国各级政府普遍拥有要素的分配权、定价权和管制权，导致要素自由流动受阻和要素价格被低估等问题，形成要素市场扭曲[1]。

从目前的研究进展看，对于创新效率的研究颇多，但多聚焦在对其的测度和评价上[2-3]。而对于影响因素的研究，关注的一般是创新主体、创新环境及单纯的要素投入等这几个方面，将市场化进程中容易忽视但由来已久的要素市场扭曲现象与创新效率相结合的文献相对较少，且多聚焦在不同类型行业尤其是工业和制造业等中观层面上[4-5]，对要素市场扭曲造成的地区差异缺乏研究。基于此，本文主要着眼于在中国市场化进程的大背景下，要素市场扭曲对地区创新效率产生了何种影响这个问题。

1 理论分析与研究假设

在完全竞争条件下，要素价格由要素市场的供求关系决定，并能准确反映要素的稀缺程度及动态变化。然而当要素市场处于扭曲状态时，会导致要素价格失真，使企业不能根据比较优势选择适合自身发展的产业和技术，对要素的配置无法达到帕累托最优状态，从而抑制了创新效率。本文将主要从劳动力市场和资本市场2个角度来探讨。

1.1 劳动力市场扭曲与创新效率

从劳动力市场扭曲的角度看，其对区域创新效率的影响主要通过“就业抑制效应”、“低端锁定效应”以及“人才挤出效应”影响地区创新效率的变化。

劳动力市场扭曲通过“就业抑制效应”影响创新人才的空间配置，抑制区域创新效率的提升。虽然随着我国户籍制度的放开，劳动力有了大规模流动[6]，但户籍歧视伴随医疗教育等公共服务的地区差异及等人为因素，劳动力市场分割问题并未完全消除，造成地区科技创新人才空间配置水平低下[7]。

劳动力市场扭曲通过“低端锁定效应”影响区域创新效率。地方政府为保护本地利益，普遍漠视普通劳动者的权益被侵占现象，默许压低劳动者的工资，一方面让企业更倾向于使用有形要素，止步于原有的固定生产模式，另一方面也降低了劳动者的收入水平，造成地区劳动者需求层次的偏低，使企业的创新支出不能得到弥补，反过来削弱企业进行创新活动的动力。

劳动力市场扭曲通过“人才挤出效应”影响地区的人力资本水平。劳动力价值的“剪刀差”虽在短期能获得一定的竞争优势，但对低收入劳动者而言，收入水平过低会直接抑制其在家庭教育及自身技能提升等方面的投入，阻碍地区高素质创新人才的涌现[8]。而对于高收入劳动者群体来说，容易使其丧失进行生产活动的积极性导致产出低下，甚至导致人才从本地区流出。

1.2 资本市场扭曲与创新效率

从资本市场扭曲的角度看，其对区域创新效率的影响主要来自其对创新资本配置的干扰、诱发的“非生产性寻租”活动以及对企业创新需求的抑制导致的创新效率损失。

资本市场扭曲通过资源错配效应降低了创新资源的配置水平，进而抑制创新效率。资本市场扭曲主要从2个方面影响资本的配置水平：一是在政府 “晋升锦标赛”激励的约束下，倾向于能快速实现经济效益的一般生产性项目，通过强制干预金融机构的信贷决策形成金融抑制;二是资本市场扭曲释放出的虚假信息等信号，让金融资源财政补贴和税收减免等无法按市场规律流入边际生产率更高的领域。

资本市场扭曲诱发“非生产性寻租”[9]活动，通过“挤出效应”削弱区域整体创新效率。在一元金融资本体系结构下，政府部门对资本要素拥有配置权和定价权，由此带来了寻租空间。为了获得融资自由，企业拥有强烈动机去进行非生产性寻租，在这过程中，消耗了大量的人力和财力等资源，挤占创新资源。

资本市场扭曲通过需求抑制效应影响企业的创新效率，在面临资本市场扭曲的情况下，国有企业获取资金的成本较低，容易盲目追求规模扩张而忽略创新，造成产能过剩和创新能力不足。而大量中小企业，尤其是在创业初期的高科技企业，由于高风险性及缺少抵押资产，难以获得银行的信用融资[10]。即使能够获得创新融资，融资成本高昂也让其难以获得创新收益，不得不降低自身创新需求。

1.3 要素市场扭曲与区域创新效率关系的进一步思考

由于我国不同经济板块的开放时间不同，政府对要素市场的干预力度也存在差异，可能造成要素市场扭曲程度也存在着区域上的显著差异[11]。对于要素市场扭曲程度较高的地区，要素市场分割及要素价格扭曲水平更为严重，一方面让区域内部要素错配对创新生产的抑制作用效果更为显著;另一方面也会更深层次地抑制企业的创新生产积极性，将更多的要素投入到非生产性活动及一般性的生产项目。与之相反，在要素市场扭曲程度较低的区域，单位要素所能维持的边际产出依然较高[12]，企业进行寻租活动的空间相对较小，对创新要素投入的浪费也比较有限，而此时地方政府通过促进产业结构升级淘汰落后企业的意愿会更强烈。另外，随着扭曲程度的降低，市场竞争将更激烈，企业希望通过加大创新力度来获得竞争优势的意愿较强，此时地区的创新效率可能会得到改善。

综上，本文提出如下假设：

假设1：要素市场扭曲抑制了区域创新效率的提升，且扭曲程度越高，抑制作用会越明显。

假设2：要素市场扭曲对区域创新效率的影响存在地区异质性。

2 模型设定与指标选择

2.1 模型设定

2.1.1 随机前沿模型

目前，学者们对于创新效率的测算主要有数据包络分析[13]和随机前沿法。其中，随机前沿模型结合了生产函数与随机因素，使测算结果更加接近实际情况。对随机前沿生产函数的选择，本文构建了超越对数生产函数，因为其放宽了技术中性与产出弹性固定等严格假定，形式更为灵活，还能够避免函数形式设定错误而造成估计偏差。具体模型可表达为

ln yit=β0+βKln Kit+βLln Lit+βτt+

12βKK（ln Kit）2+12βLL（ln Lit）2+12βττt2+

βKLln Kitln Lit+βTKtln Kit+βTLtln Lit+vit-uit。（1）

其中：i代表地區;t代表年份;β0为常数项;βK，βL，βT，βKK，βLL，βTT，βKL，βTK，βTL分别表示劳动力，资本，时间和各二次项的回归系数;vit和uit相互独立，vit表示服从独立同分布的随机扰动项，uit表示技术非效率项。因为模型设定是否恰当极大地影响结论科学性，所以对模型做如下检验，即随机前沿模型的适用性检验、生产函数形式检验、技术进步检验、技术非中性检验以及技术效率的时变性检验。

2.1.2 ESDA空间自相关检验

考虑到目前创新活动存在明显的空间正相关性特征，忽略空间异质性假设可能导致研究结论出现偏差，为更好地解释区域创新效率的空间分布状况及其与要素市场扭曲的关系，本文将引入空间计量分析法进行分析。而是否有必要在模型中引入空间因素，一般先用Morans I指数来测度其空间关联程度，其计算式为

Morans I=∑ni=1∑nj=1Wij（yi-y）（yj-y）S2∑ni=1∑nj=1Wij。（2）

其中：y与S2分别为区域创新效率及其方差;Wij为空间权重矩阵。考虑到地理位置上邻近但实际上并不相邻的省域之间的相互影响，在此选择反距离空间权重矩阵。Morans I的取值范围为[-1，1];若非负，说明存在正空间自相关性;若为负，说明存在负空间自相关性;若等于0，表示目标区域在空间上呈随机分布。

2.1.3 空间面板模型

常用的空间计量经济模型，主要是空间滞后模型（SLM）和空间误差模型（SEM）。SLM探讨邻近地区被解释变量对本地区被解释变量的影响，其基本表达式为

yit=α+ρWyjt+βiχit+εit。（3）

其中：y是被解释变量;ρ是空间滞后系数;W是空间权重矩阵;χ是解释变量;β是待估参数;ε是随机误差项。

SEM的空间依赖关系则存在于扰动误差项中，探讨邻近地区因变量的误差冲击对本地区因变量的影响。其表达式为

yit=βiχit+εit。

εit=βγWεit+uit。（4）

其中：y是被解释变量;χ是解释变量;β是待估参数;γ是空间误差系数;W是空间权重矩阵;u是随机误差项。

2.2 数据说明与变量选择

2.2.1 数据说明

本文选取的研究样本为1998—2016年中国30个省级面板数据，为了便于资本存量化的处理，将重庆并入四川，西藏由于大量数据缺失，不予研究。原始数据主要来自历年《中国统计年鉴》、《中国科技统计年鉴》及EPS数据平台。

2.2.2 变量选择

1）创新效率。将其表示为实际产出期望值和最优前沿面的期望值之比，即：

TE=E[f（RDKit，RDLit）exp（vit-uit）]E[f（RDKit，RDLit）exp（vit）|uit=0]。（5）

其中：i和t分别为地区和年份，K和L为创新资本和劳动力的实际投入。若uit=0，则创新生产处在最佳前沿面f（Kit，Lit，t）exp（vit，uit=0）上。本文选择专利授权数来衡量创新产出，同时参考白俊红等[14]的研究，根据创新程度对发明、实用新型和外观设计专利分别赋予0.5、0.3和0.2的权重。另外，选取R&D人员和R&D资本存量作为创新投入指标。其中，R&D人员用R&D人员全时当量来衡量，因为创新活动的连续性，对R&D经费内部支出做存量化处理。

2）要素市场扭曲。现有文献对要素市场扭曲的测度方法主要有生产函数法、DEA法和市场化指数法等，生产函数法较其他方法而言，经济含义明确，且其可行性经过经典理论和实证充分验证，并可直接测算资本和劳动逐期的边际产出。因此，本文选择CD生产函数来测度要素扭曲，模型构建如下：

ln Yit=ln Ait+αtln Kit+βtln Lit+μt。（6）

其中：Yit，Kit，Lit分别为实际产出，资本和劳动力要素投入，Ait为技术水平。根据估计出来的生产函数，可计算出每期各要素的边际产出，最终得到要素边际产出与其实际价格的比值。本文中

Yit，Kit，Lit，Ait分别用地区生产总值、全社会固定资产投资、年末就业人数和第三产业占比来衡量。为了消除价格因素的干扰，将地区平减为以1998年为基期的价格。对资本存量的测算借鉴单豪杰[15]的方法，采用永续盘存法按1998年的不变价格计算，具体用以下式折算：

Kit=Kit-1（1-δit）+Iit。

其中：Kit、Iit分别表示为以1998年不变价格表示的i地区第t年的资本存量K和固定资产投资I，δ为经济折旧率，取10.96%。

3）控制变量。借鉴以往研究，本文主要从以下几个方面进行考察：政府影响力（goi）、产业结构（ie）、技术成果转化水平（tem）及地区对外开放水平（open）。分别用各省份财政科技支出占总支出比重、国有全社会固定资产投资占比、技术市场成交额和fdi占地区GDP比重来衡量。为了消除价格因素影响，将技术市场成交额用居民消费价格指数平减为1998年不变价。对于fdi占地区gdp比重的变量处理，将fdi用当年人民币对美元的实际汇率换算成人民币，再除以地区当年gdp。

3 实证结果分析

3.1 SFA检验及结果分析

如前文所述，对SFA模型设定的合理性进行检验，主要包括：随机前沿模型的适用性检验，模型原假设H0 为：γ=0。如果接受原假设，则模型不存在无效率项，反之拒絕原假设，无效率项存在，随机前沿模型具有适用性;生产函数形式检验，若模型中所有的二次项系数为零（H0），则函数应为CD形式，否则采用Translog生产函数形式;技术进步检验，检验模型是否存在技术变化;技术非中性检验，检验技术变化是否存在希克斯中性，原假设设定时间变量与投入变量的交互项系数为零，如果接受原假设，则模型变化为希克斯中性，反之技术变化与投入要素相关;技术效率的时变性检验，如果接受原假设η=0，表明技术效率不受时间变化的影响，反之亦反。上述检验结果，如表1所示。

由检验结果可得，上述5个假设均不成立。同时，γ=0.848，在1%的置信水平上显著，由此可以推断技术非效率项对区域创新效率具有显著影响，且在影响区域创新效率的随机因素中，技术非效率可解释其中的84.8%。所以本文应选择超越对数随机前沿模型进行估计，无法简化为CD函数形式。在此也给出了随机前沿生产函数中各参数的估计结果，如表2所示。

3.2 区域创新效率描述

3.2.1 区域创新效率的时空变化特征

利用Frontier41xp1软件可实现区域创新效率的测度，1998—2016年中国及3大地区创新效率的变动情况，如表3所示。1998—2016年我国创新效率提升较为明显，由“九五”期间的0.274增至“十二五”期间的0.420，增长态势较为强劲。东部地区创新效率一直高于全国平均水平，从1998年的0391增至2016年的0.571，增速达46.04%。中部和西部亦有较大提升，其中西部地区由于起点较低，增幅高达107.19%。但是从绝对值来看，中国整体的区域创新效率还处于较低水平，创新发展质量有待提高。

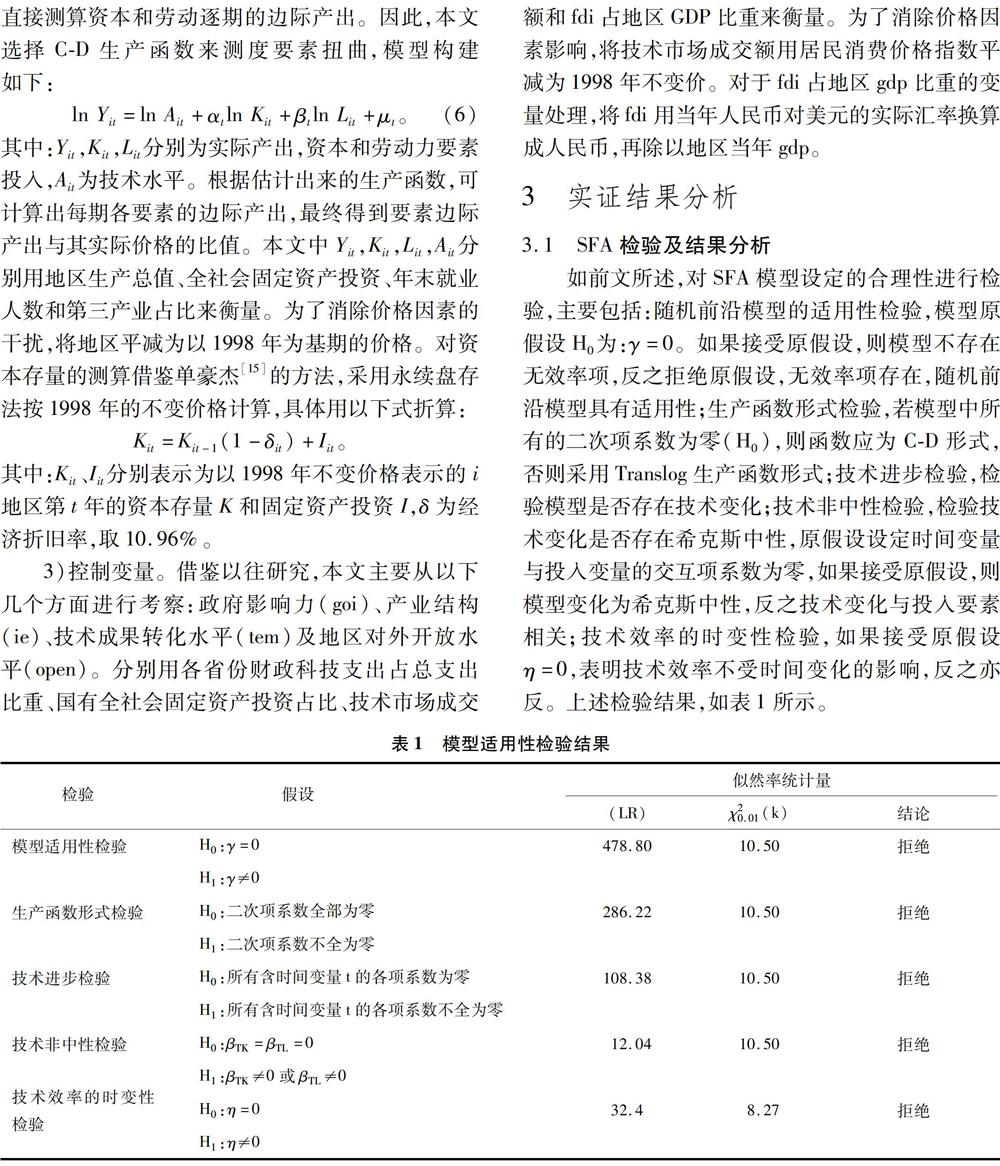
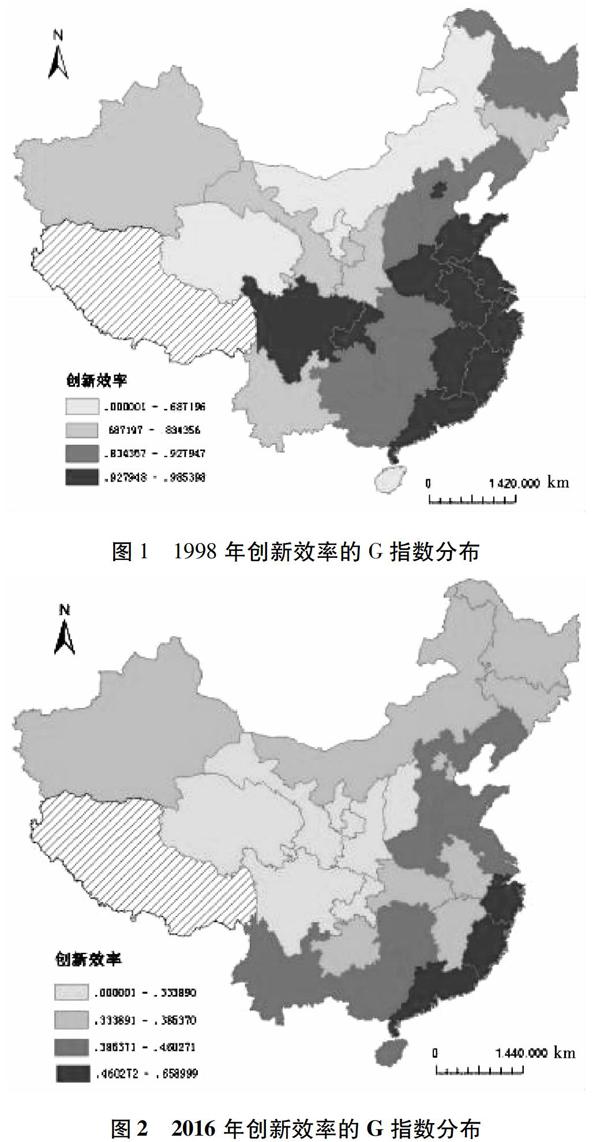
为进一步从空间演化角度分析区域创新效率的分布特征，利用Arcgis10.2软件对1998与2016年各省创新效率进一步对数据进行可视化处理，用自然断裂法将数值由低到高分为4类，分别为：冷点区、次冷区、次热区、热点区。通过对比可以发现：1998年创新效率热点区主要分布在东部沿海省份，主要为广东、浙江、福建，2016年扩大到江西、安徽、江苏等地区，北京则成为一个独立的热点区，总体来看，热点范围显著扩大;从冷点区看，1998年主要分布在四川、青海、甘肃、陕西等西部地区，2016年冷点地区明显缩小，只剩下青海、内蒙古和宁夏;次冷地区仍占据较大范围。

3.2.2 区域创新效率全局空间相关性分析

运用Geoda软件测度区域创新效率的Morans I指数，如表4所示。1998—2016年，全局Morans I指数为正，且在1%的置信水平上显著，这说明我国区域创新效率存在着显著的正空间自相关性。即对于创新效率相对较高的省份，往往存在着一个或多个高值省区与之相邻（高—高正相关）;相应地，创新效率低值省区也趋向于与低值省区相邻（低—低正相关）。另外，样本考察期内，Morans I指数均在0.25上下波动，说明我国省域创新效率关联效应不仅强且较为稳定。

3.3 模型回归结果及分析

3.3.1 总样本回归结果

根据ESDA空间自相关检验，区域创新效率在空间上存在依赖性。所以，采用传统经典估计方法得到的结果将有偏，应该运用空间计量经济模型进行估计。对模型进行Hausman检验后，P值为0.000 0，故采用固定效应进行回归估计。不同个体效应下的SLM和SEM的估计结果，如表5所示。

由表5可知，SEM模型和SLM模型都以空间固定效应为佳，但SLM模型的拉格朗日乘子、拟合优度和似然对数等统计量较SEM更为显著，说明SLM模型更为合适。故以下主要就空间滞后模型的估计结果进行解释与分析。SLM模型的解释空间滞后项系数ρ显著为正，说明表明省域创新效率存在着比较显著的空间溢出性，即邻省创新效率的提高能够带动周围省份。

从总体样本核心解释变量的回归系數来看，资本要素市场扭曲和劳动力市场扭曲的回归系数分别为-0.002 3和-0.014 4，且均在1%的显著性水平下通过了显著性检验，说明要素市场扭曲整体上抑制了区域创新效率的提升，这就验证了假设1。

控制变量中，政府影响力的回归系数整体通过了10%的假设检验，说明财政科技支出对创新效率有正向作用，现实情况下，政府对创新生产活动的干预程度越大，即政策或财政性支持越多，企业就有更多的资源去加大对创新的投入，提高创新生产水平。产业结构中，国有固定资产投资占全国比重的系数显著为负，说明市场化进程的推进有利于区域创新效率的提高。一般而言，国有企业拥有的政府支持较多，进行创新活动的积极性不高，与之相反，为在市场中获得超额利润，非国有企业进行创新研发的热情高涨。因此，随着市场化水平的提高，非国有企业所占比重越大，对于地区创新效率的提升往往有正向作用。技术市场成交额与区域创新效率均呈显著的正相关关系，说明创新成果的转化更有利于刺激创新效率的提升。地区开放水平的系数显著为正，因为对外开放水平越高，有利于外部技术的溢出，吸引更多的人才、资本和技术;也能够激发本土企业的竞争意识，对创新生产活动形成激励，从而提高创新效率。

3.3.2 区域异质性分析

为了进一步检验要素市场扭曲对不同地区的影响关系及验证结论稳健性，本文进行了东中西部回归分析，结果显示，要素市场扭曲对不同地区存在异质性影响：从劳动力市场扭曲的回归系数看，劳动力市场扭曲明显抑制了西部地区的创新效率的提升，对东中部地区则不太显著，可能是因为西部地区教育落后，人力资本相对低质有关。与之相反，资本市场扭曲对东部地区的负向作用更加显著，中部地区的回归系数为正但不显著，西部地区的回归系数为负但绝对值小，这是因为东部地区经济相对发达，区域内部的企业往往已经拥有一定的自生能力，这时政府干预资本市场会造成更大的资源配置低效，这就验证了假设2。控制变量中，政府的财政支持的回归系数在中部地区显著为负，在西部地区为负但不显著，这可能是因为中西部地区的市场竞争相对较弱，政府补贴可能在一定程度上造成了域内企业的创新惰性;国企占比对东中部的抑制作用更强，这也与企业的自生能力有关。

4 结论与建议

在对要素市场扭曲与区域创新效率二者关系进行理论分析后，本文运用空间计量模型来探讨要素价格扭曲与区域创新效率的关系。研究表明：1）劳动力和资本市场扭曲对区域创新效率整体上起抑制作用。2）劳动力市场扭曲更明显地抑制了西部地区的创新效率，而资本要素市场扭曲则对东部造成了更大的创新效率损失。3）财政科技支出的增加，创新成果的技术转化和良好的对外开放水平可以提升区域创新效率;而国有企业所占比重的提高则会阻碍市场化进程的推进，对区域创新效率起抑制作用。基于此，本文提出如下针对性的政策建议：

1）对于东部地区，应重点关注资本要素市场扭曲的问题，大力促进资本自由流动和利率市场化改革，从而提高资本要素的配置水平;对于中西部地区，更应该提高现有的工资水平来吸引并留住高素质劳动力，同时缓解地区资源不同而人为造成的要素市场分割，为区域创新效率的提升提供良好环境。

2）东部发达地区应继续提高自主创新水平，逐渐摆脱对外技术的依赖，成为我国的创新引领区;中部地区应重视科技创新水平方面的合作和提高吸引外资先进技术的能力;西部地区还需完善基础设施和重视人力资本的积累，现阶段还可以通过承接产业转移和技术模仿来实现科技创新。

3）西部地区资本相对稀缺，应加大对其的科研资金投入，但在这过程中需要严格把控资金的具体流向，防止因寻租和虚假信息等因素造成的资源浪费;而东中部地区资本相对充足，应制定良好的产业政策从而提高区域整体的创新实力。

4）东中部地区的技术成果转化的水平较高，需重点关注知识产权和专利的保护，同时吸引更多的外国优秀企业，激发本土企业的创新活力和竞争意识;西部地区在创新成果的市场转化和成本弥补上还需加强，目前还可以学习优秀创新型企业先进的管理模式和技术模仿，为新时期创新驱动战略打下良好的基石。

参考文献：

[1] 张杰，周晓艳，李勇.要素市场扭曲抑制了中国企业R&D？[J].经济研究，2011（8）：78.

[2] 王宁，史晋川.中国要素价格扭曲程度的测度[J].数量经济技术经济研究，2015（9）：149.

[3] 仲任.中国制造业要素价格扭曲研究：来自A股制造业上市公司的经验数据[J].科技与管理，2017（3）：41.

[4] 戴魁早，刘友金.要素市场扭曲与创新效率：对中国高技术产业发展的经验分析[J].经济研究，2016（7）：72.

[5] 余东华，孙婷，张鑫宇.要素价格扭曲如何影响制造业国际竞争力[J]，中国工业经济，2018（2）：63.

[6] BRANDT K，TREVOR T，ZHU X D.Factor market distortions across time， space and sectors in China[J].Review of Economic Dynamics，2013（16）：39.

[7] 白俊紅，卞元超.要素市场扭曲与中国创新生产的效率损失[J].中国工业经济，2016（11）：39.