高地温隧道荷载模式及二次衬砌安全特性研究
2019-12-13王明年王奇灵胡云鹏王翊丞刘大刚
王明年, 王奇灵, 胡云鹏, 王翊丞, 刘大刚
( 1. 西南交通大学土木工程学院, 四川 成都 610031;2. 西南交通大学 交通隧道工程教育部重点实验室, 四川 成都 610031 )
0 引言
随着交通强国战略的实施,在我国地质状况复杂的西部山区出现了大量超长的公路(铁路)隧道,而川藏线上隧道建设所面临的工程问题尤为突出。川藏铁路跨越我国二三级阶梯,隧线比极高,同时受到各种特殊地质的挑战,如高地温、岩爆、冰碛层等,特别是高地温引发的隧道施工环境恶化、锚杆抗拔力不足、支护结构安全性降低等问题十分突出。
目前,已有学者针对高地温隧道温度场变化规律、支护结构力学特性、材料劣化特性和支护结构形式等开展了相关研究。其中: 周小涵等[1]根据能量守恒原理,建立了空气-衬砌-围岩的二维非稳态有限差分方程,分析了季节性风温、不同初始地温等对于高地温隧道传热的影响;肖琳等[2]通过室内模型试验模拟了地铁隧道内的热传导,研究了地铁围岩内温度分布规律,并反算了热导率;张先军[3]以昆仑山隧道为依托工程,通过长期现场监测,获得了寒区隧道隔热层内外侧温度随季节的变化规律;邵珠山等[4]采用量纲一化和微分方程级数求解的方法,建立了隧道二维稳态热传导方程,得到了包含温度场、位移场和应力场的热弹性理论解;刘乃飞等[5]以布伦口水电站高温引水隧洞为背景,通过解析法探究了高温下围岩及支护结构的受力特性;陈勤等[6]以溪洛渡泄洪隧洞为对象,借助有限元计算软件,探究了温度应力对于衬砌受力及开裂情况的影响;CUI S.等[7]结合室内模块试验和电镜扫描技术,对比研究了普通喷射混凝土以及掺加粉煤灰或硅粉的混凝土在高温环境下的强度变化规律;何廷树等[8]通过模块试验研究了不同龄期、不同掺合料混凝土的强度特性,并借助XRD和SEM测试手段分析了胶凝材料反应速度以及扩散和致密程度;白国权等[9]通过数值模拟,针对高地温隧道隔热材料的类型和厚度进行了比选;王明年等[10]以吉沃希嘎隧道为工程依托,通过数值模拟,以热害等级、隔热降温效果和衬砌受力特性为依据对高地温隧道的支护结构形式进行了分级。
目前,针对高地温隧道的研究主要集中在隧道温度场与应力场变化规律的理论和试验研究,以模块试验和微观扫描技术为基础的混凝土在高地温环境下材料性能研究,综合材料试验和数值模拟的高地温支护结构形式研究[11-14],但针对高地温隧道荷载模式研究鲜有报道。因此,本文以川藏线桑珠岭超高地温隧道为工程依托,通过现场试验和数值模拟,提出了一种高地温隧道的荷载计算模式,并研究了高地温隧道二次衬砌的安全特性,以期为高地温隧道的设计和施工提供指导。
1 工程概况
川藏线桑珠岭隧道位于西藏桑日县桑加峡谷区沃卡车站至巴玉车站之间,隧道全长16 449 m,最大埋深达1 480 m,平均海拔约为3 700 m。隧道沿线穿越沃卡断裂带,与羽张断裂带相距5~8 km,地层以花岗岩、闪长岩等坚硬岩体为主,岩体破碎,地下水发育,隧道平面如图1所示。隧道采用钻爆法施工,全程共设置3个辅助坑道,多断面同时进行施工。其中,1#横洞开挖至81 m处出现高地温情况,探孔内温度最高可达89 ℃。岩石表面温度最高可达74.5 ℃,采取降温措施后环境温度达43.6 ℃,属超高地温隧道。

图1 桑珠岭隧道平面图
2 现场试验
对桑珠岭隧道支护结构的力学性能展开研究,共选取2个试验断面的初期支护和二次衬砌进行应力应变测试,试验断面里程分别为D1K175+103和D1K175+125。
2.1 监测点布置
测试断面宽8.26 m、高10.43 m,均为Ⅴ级围岩。初期支护厚度为0.25 m,二次衬砌厚度为0.45 m。对于初期支护,分别在左边墙、左拱腰、拱顶、右拱腰和边墙处埋设1个应力应变计,位于初期支护中部;对于二次衬砌,分别在左边墙、左拱腰、拱顶、右拱腰和右边墙处埋设2个应力应变计。监测点布置如图2所示。分别监测各位置内外侧应力的变化情况。
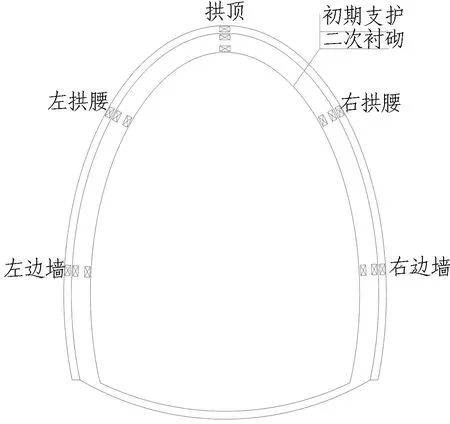
图2 监测点布置
2.2 测试方案
隧道爆破出渣立拱完成后,便进行试验仪器的安装。应变计在完成初始读数后,通过扎带绑扎于钢拱架上。初期支护监测时间为30 d,初始测试频率为1次/d,稳定后为1次/3 d。随着隧道不断开挖,当二次衬砌进度到达试验断面时,进行二次衬砌混凝土应力应变计的安装。二次衬砌监测周期为30 d,初始测试频率为1次/d,稳定后为1次/3 d。现场试验如图3所示。

(a) 混凝土应力应变计

(b) 初期支护仪器安装

(c) 二次衬砌仪器安装

(d) 数据采集
图3现场试验
Fig. 3 Field test
2.3 试验数据分析
通过对2个试验断面各自初期支护和二次衬砌应力的长期监测,获得了相关结构各部位应力变化的时程曲线,如图4和图5所示。
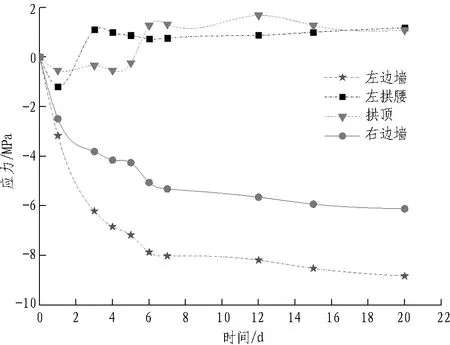
(a) 断面1初期支护喷混凝土应力时程曲线
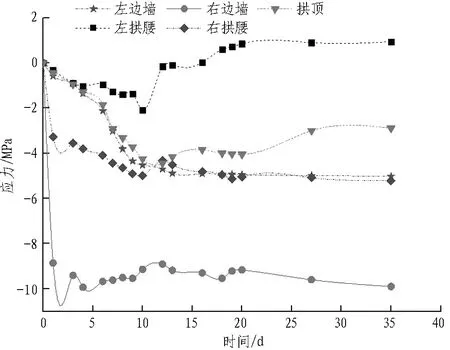
(b) 断面2初期支护喷混凝土应力时程曲线
图4初期支护应力时程曲线
Fig. 4 Time-history curves of primary support stress
由图4可知: 试验断面1中,应力在7 d内变化较快,15 d后基本稳定; 最大压应力为8.83 MPa,位于左边墙,最大拉应力为1.18 MPa,位于左拱腰。试验断面2中,应力在10 d内变化较快,18 d后基本稳定; 最大拉应力为0.94 MPa,位于左拱腰,最大压应力为9.90 MPa,位于右边墙; 拱顶和右拱腰处的应力随着开挖进尺而逐渐增大并最终稳定,其中拱顶应力增长幅度最大; 边墙处应力可能出现应力特性变化的情况,由受压变成受拉。
由图5可知: 试验断面1中,二次衬砌混凝土外侧应力在前8 d变化较快,12 d后基本稳定,左拱腰和拱顶受拉,其余各部位受压,最大压应力为2.08 MPa,位于右边墙,最大拉应力为0.56 MPa,位于拱顶;二次衬砌内侧应力在前6 d变化较快,12 d后趋于平稳,其中,最大压应力为1.46 MPa,位于左边墙,最大拉应力为0.62 MPa,位于拱顶。试验断面2中,内外侧应力均在10 d内变化较快,20 d后稳定,外侧最大压应力位于右边墙,数值为2.65 MPa,最大拉应力为0.50 MPa,位于拱顶;内侧最大压应力为1.06 MPa,位于右边墙,最大拉应力为0.90 MPa,位于拱顶。2个试验断面中,二次衬砌应力均在10 d内变化较快,20 d后趋于稳定。最大拉应力均位于拱顶处,且内侧最大拉应力大于外侧最大拉应力,而最大压应力常出现在边墙处。
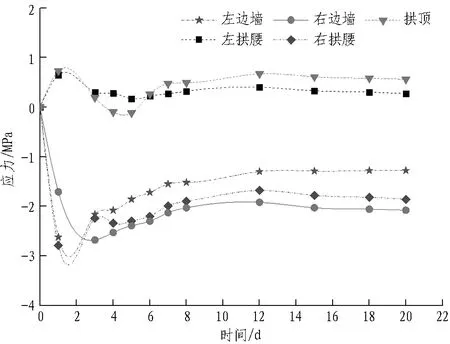
(a) 断面1二次衬砌混凝土外侧应力时程曲线
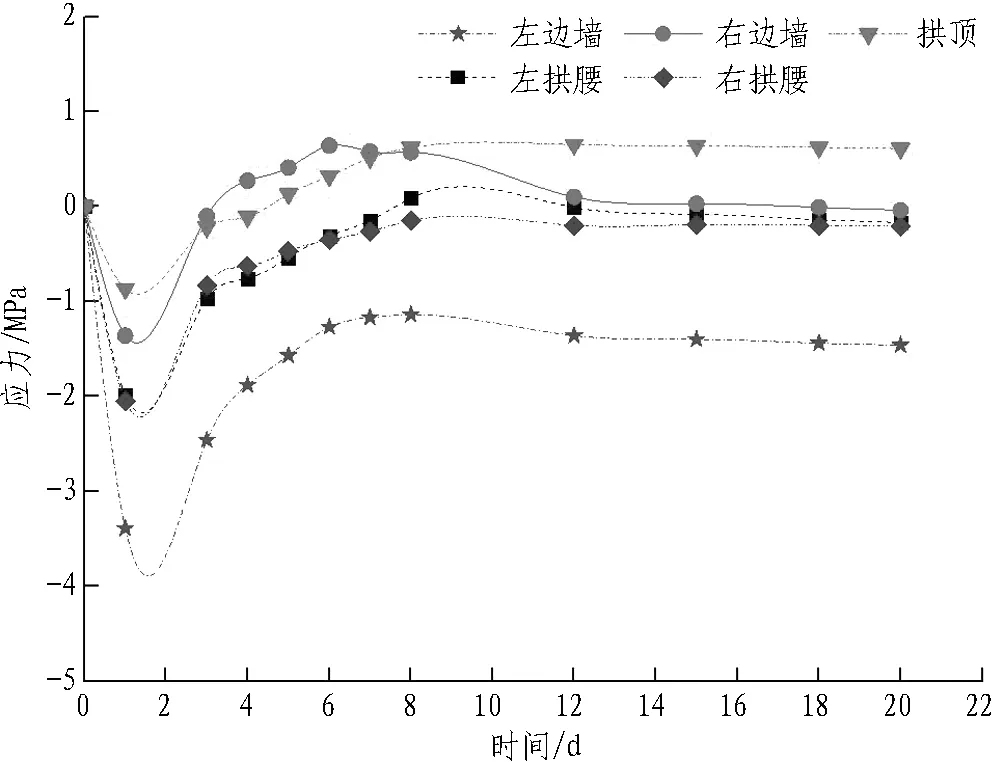
(b) 断面1二次衬砌混凝土内侧应力时程曲线
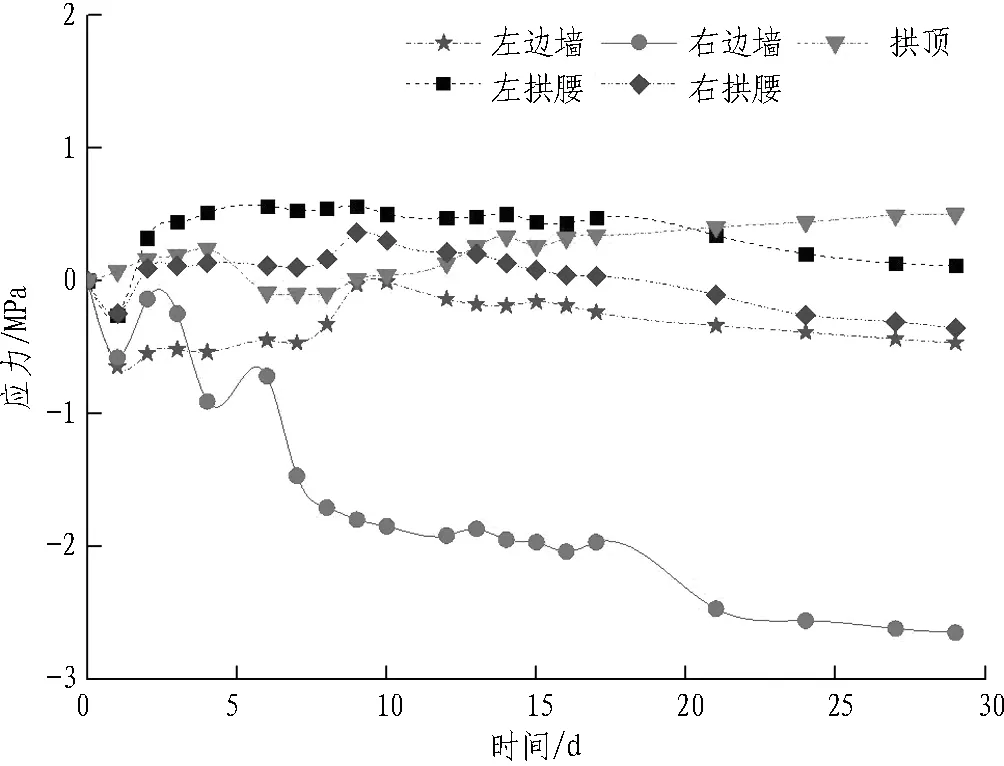
(c) 断面2二次衬砌混凝土外侧应力时程曲线
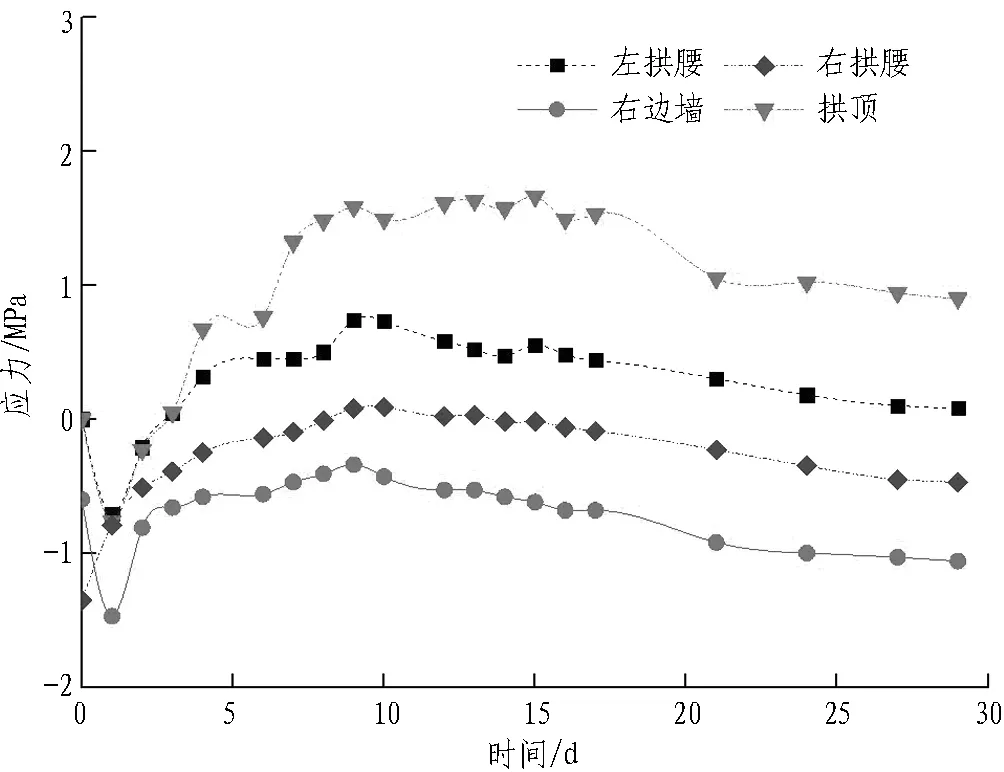
(d) 断面2二次衬砌混凝土内侧应力时程曲线
图5二次衬砌应力时程曲线
Fig. 5 Time-history curves of secondary lining stress
3 高地温荷载模式确定
通过Flac3D软件建立高地温隧道开挖和支护的三维热-力耦合模型,并将数值计算结果与现场试验进行对比验证。通过提取接触面的压力确定高地温隧道的荷载模式。
3.1 计算模型及参数
Flac3D中的热-力耦合计算模型可以同时对单元赋予力学和热学参数。计算原理以能量守恒定律为基础。高地温隧道衬砌结构温度附加应力源于超静定结构在高温下产生的应力以及衬砌和围岩间不协调变形产生的挤压应力。Flac3D中的热力单元计算原理能够较好地模拟该物理力学机制。模型中隧道围岩为Ⅴ级,埋深100 m,隧道模型底部围岩厚40 m,左右两侧宽度取为5倍的隧道跨度,约40 m,纵向长度为40 m,纵向单元长度为1 m。环向网格采用辐射状划分,尺寸由内向外逐渐变大。模型中隧道断面及支护结构尺寸与桑珠岭隧道实际尺寸相同,开挖循环进尺设为2 m,同时在初期支护和围岩之间建立接触面,计算模型如图6所示。通过对材料导热系数的测试(见图7),获得材料相关热学参数,其余参数依据规范和现场设计资料进行取值,以确保模型参数的准确性。具体参数如表1所示。
以围岩初始温度进行工况划分,共设置6种工况,如表2所示。围岩初始温度与相应工况对应,开挖后空气温度设定为28 ℃。为减少边界效应影响,选取开挖段中部断面为分析断面,并设置5个分析点,分别为拱顶、拱肩、拱腰、边墙、墙脚(因模型对称,只监测一侧),如图8所示。模型力学边界设为全约束边界,边界温度设为与工况对应的温度值,且恒定不变。
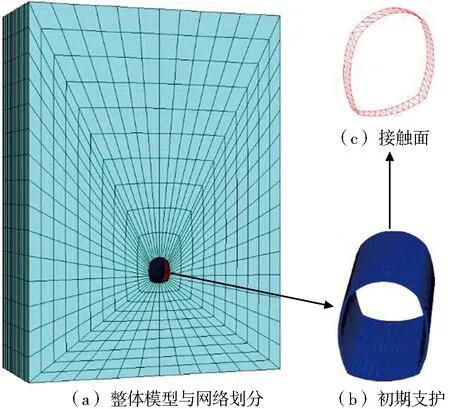

表1 热力学参数
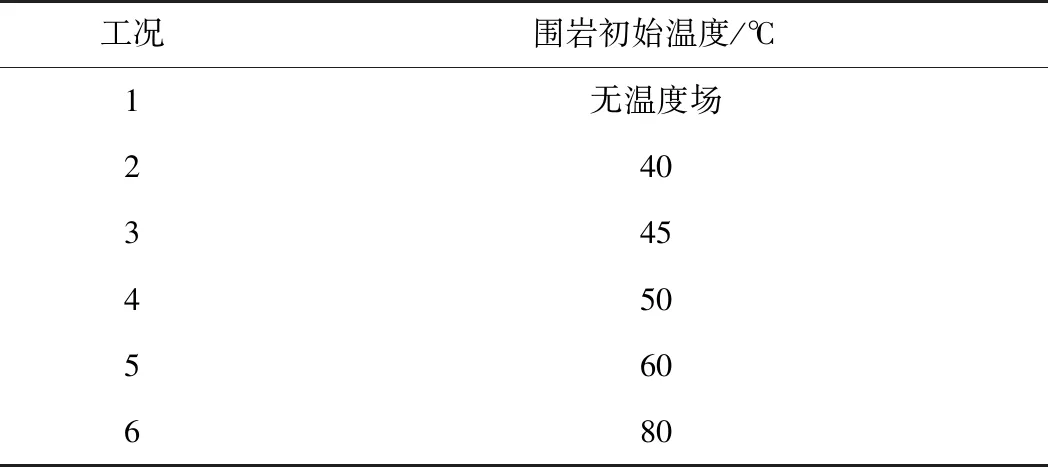
表2 结构受力计算工况统计
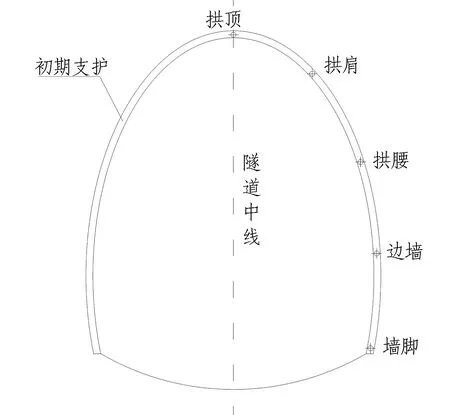
图8 分析点布置
3.2 模型与实测对比
现场实测围岩温度为45 ℃,因此将现场实测的初期支护应力与对应工况(围岩温度为45 ℃)下数值计算结果进行对比,如图9所示,并归纳总结,见表3。
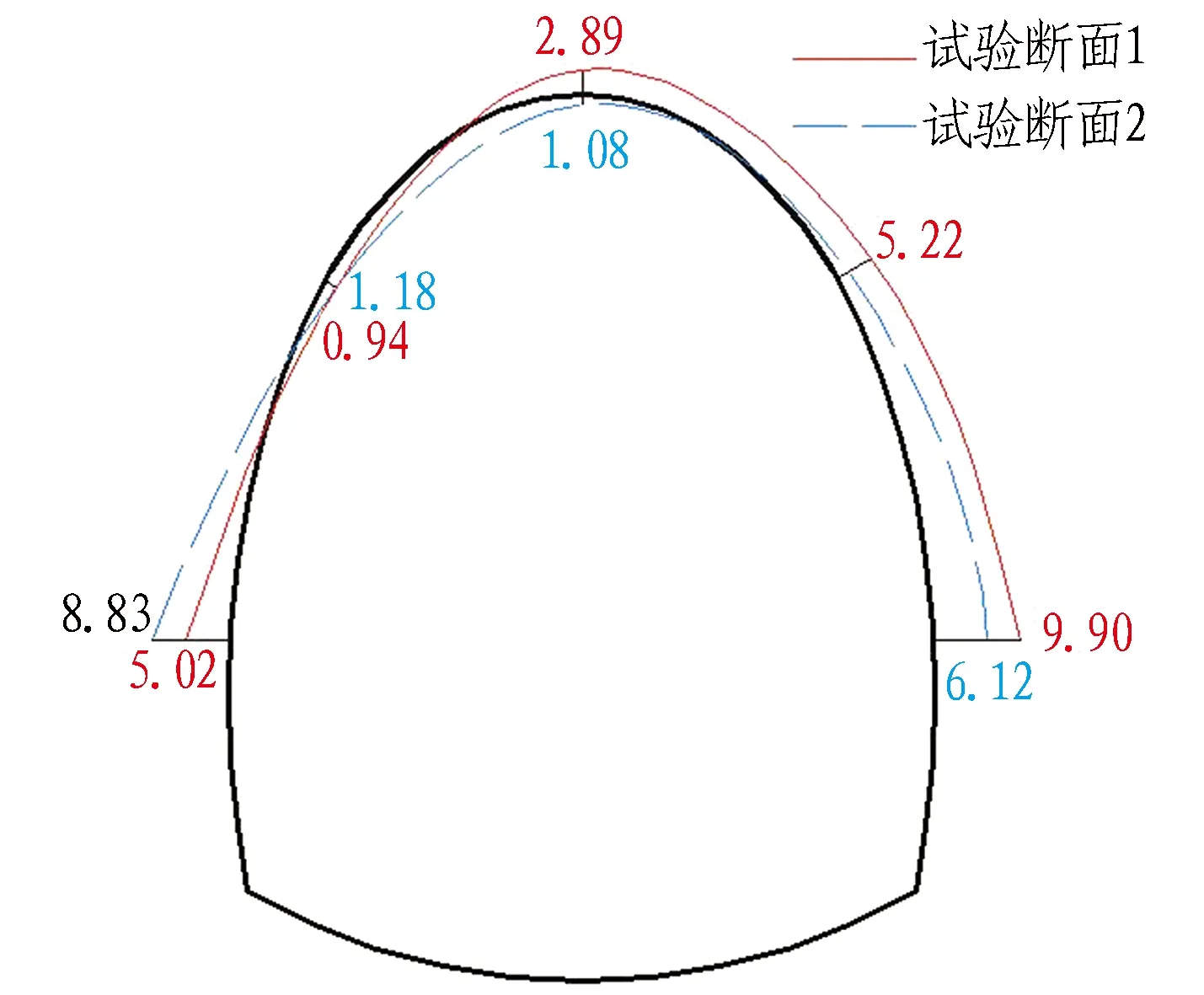
(a) 现场实测应力分布
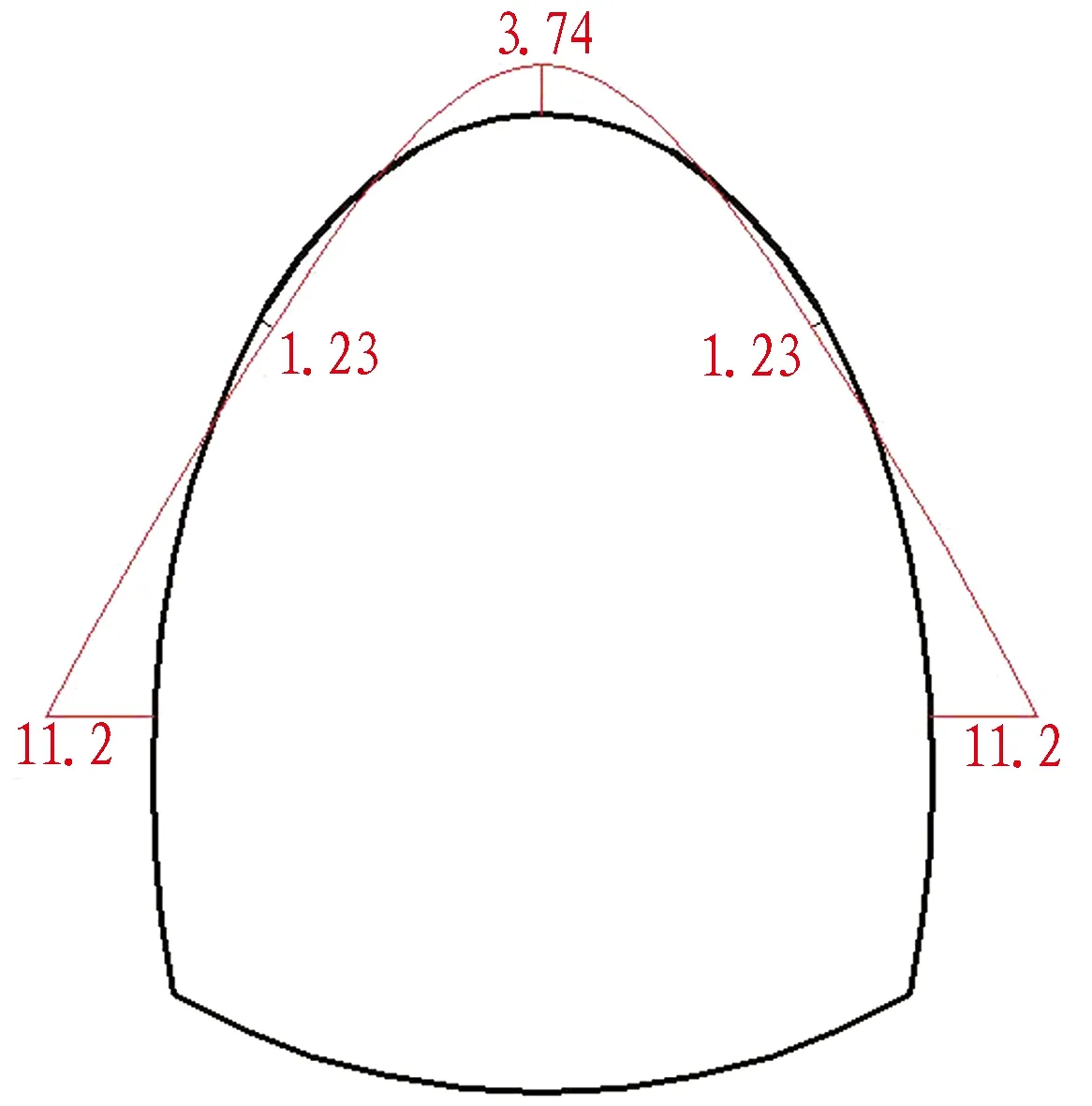
(b) 数值计算应力分布
Fig.9 Comparison between field test and simulation results (unit: MPa)

表3 实测结果与数值模拟结果对比
数值计算未考虑地形、施工等的影响,因此所得应力沿隧道中线对称。通过对比可知,数值模拟中初期支护应力与现场实测的应力特性在分布上大致相同,压应力集中于边墙,拉应力出现在拱腰和拱顶位置。数值上,数值计算中的拉压应力均偏大,拉应力偏大4%,压应力偏大10%。通过综合比较,2种试验方法所得初期支护应力在分布和大小上大致相同,因此认为该数值计算模型能够较好地反映实际情况。
3.3 荷载模式确立
通过初期支护和围岩之间的接触面,提取衬砌结构与围岩接触面处的切向压力和径向压力,提取范围为隧道墙脚至拱顶。同时,将接触压力沿水平和垂直方向(X、Y方向)进行分解,如图10所示。将起拱线以上部分垂直方向的分力作为隧道所受的竖向压力,将拱脚至拱顶水平方向的分力作为水平压力,并通过面积等效转化为均布荷载,如图11所示。无温度场时的压力通过《铁路隧道设计规范》[15]求得,其余工况下的压力通过数值计算获得。以无温度场时的压力为基础,将其余工况下的压力与之比较,进行量纲一化处理。各工况下的竖向压力和水平压力统计结果如表4所示。同时,分析量纲一化后的垂直均布压力和水平均布压力随围岩温度的变化规律,并进行数值拟合。围岩压力数值计算结果如图12所示。
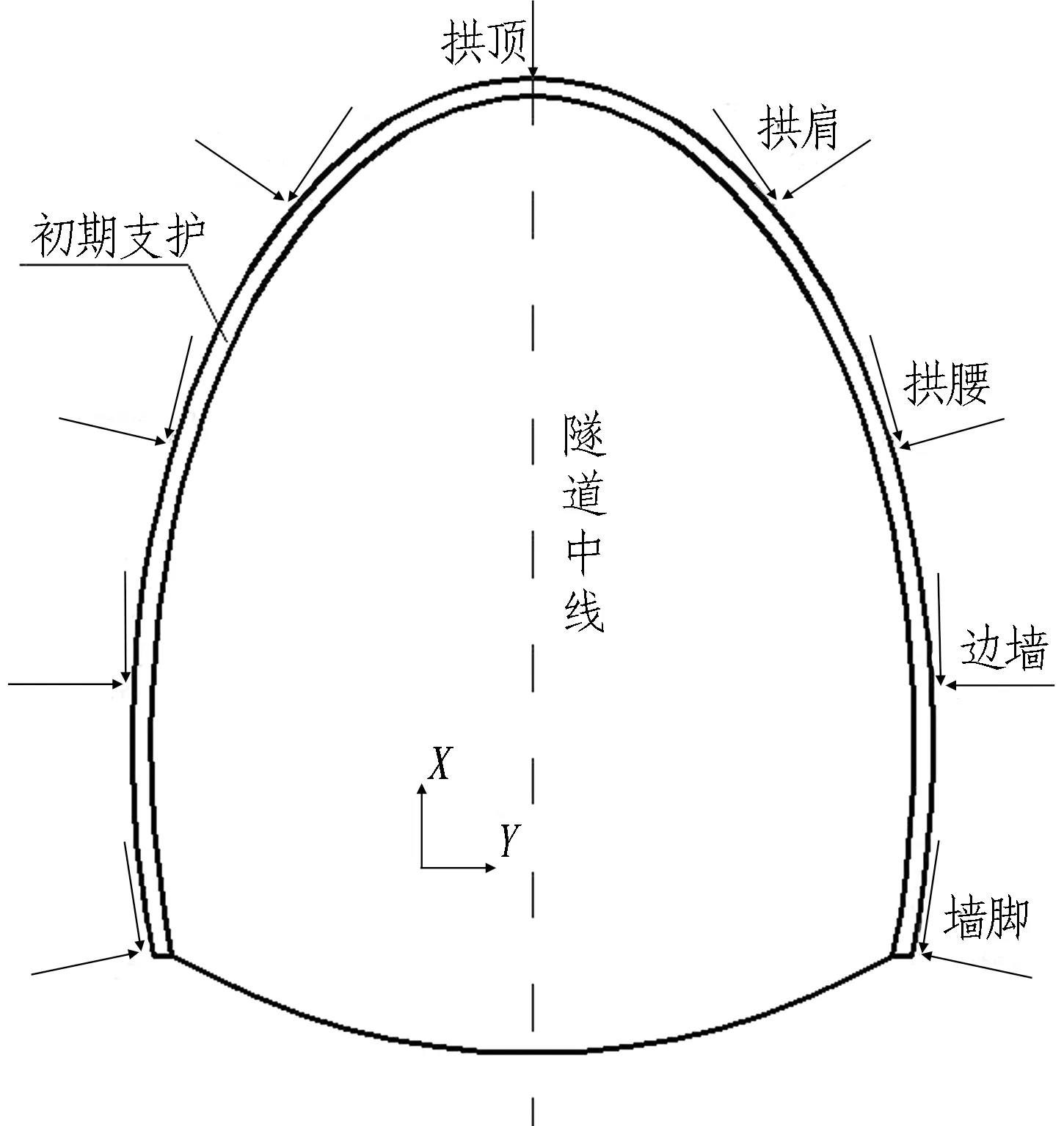
图10 围岩与初期支护接触面压力
Fig.10 Contact pressure between surrounding rock and primary support
以《铁路隧道设计规范》[15]中围岩荷载计算模式为基础,对高地温隧道中围岩的荷载模式进行修正,分别引入修正系数k1和k2。该公式只针对深埋的高地温隧道。
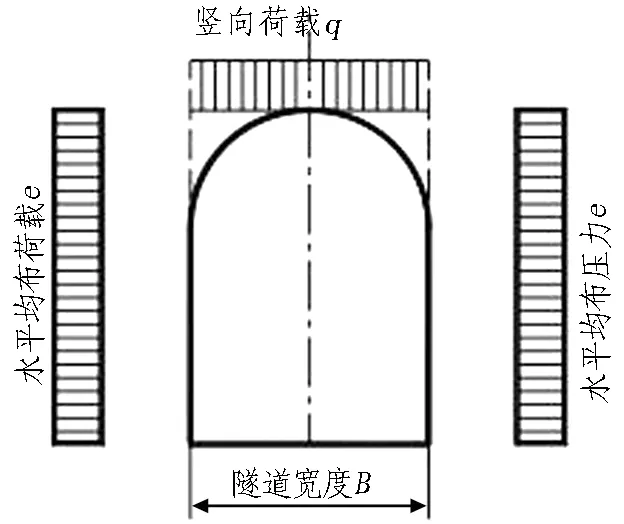
图11 荷载计算模式
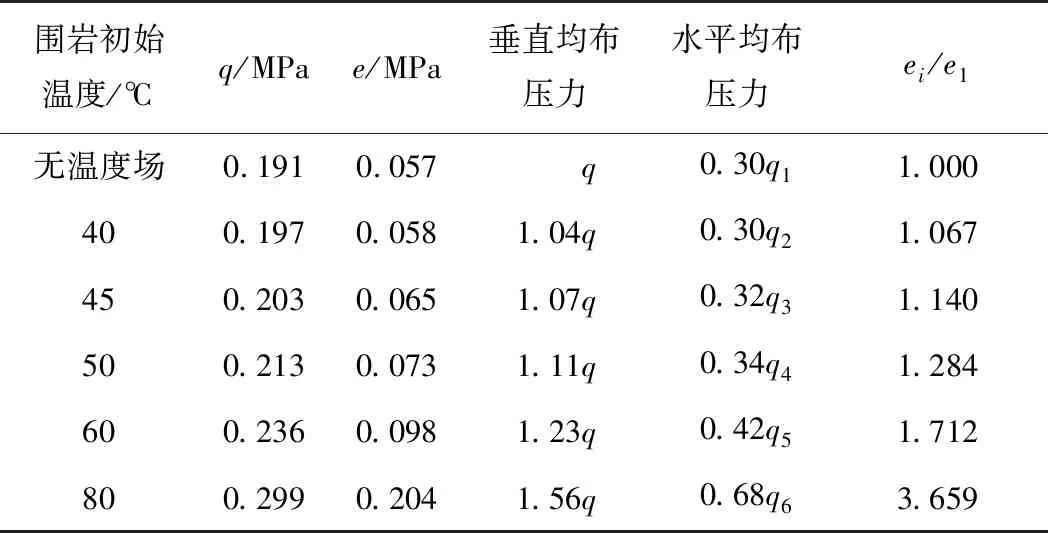
围岩初始温度/℃q/MPae/MPa垂直均布压力水平均布压力ei /e1无温度场0.1910.057q0.30q11.000400.1970.0581.04q0.30q21.067450.2030.0651.07q0.32q31.140500.2130.0731.11q0.34q41.284600.2360.0981.23q0.42q51.712800.2990.2041.56q0.68q63.659
3.3.1 垂直均布荷载修正公式
q=k1·0.45×2s-1γω;
(1)
k1=1.61×10-4t2-5.93×10-3t+1.01。
(2)
3.3.2 水平荷载修正公式
e=k2·q;
(3)
k2=1.1×10-6t3-1.28×10-5t2-1.08×10-3t+0.29。
(4)
式(1)—(4)中:s为围岩级别;γ为围岩重度;ω为宽度影响系数;t为围岩初始温度;k1为垂直均布荷载修正系数;k2为水平均布荷载修正系数。
由图12可知: 围岩垂直压力和侧压力系数均随着围岩初始温度的升高而变大; 当温度小于50 ℃时,增长速率较慢,当温度大于50 ℃时,增长速率逐渐变大。《铁路隧道设计规范》[15]中,对于Ⅴ级围岩,侧压力系数的经验取值为0.3~0.5; 而对于高地温隧道围岩,当围岩温度从40 ℃增长到60 ℃时,侧压力系数从0.3增大到0.42。
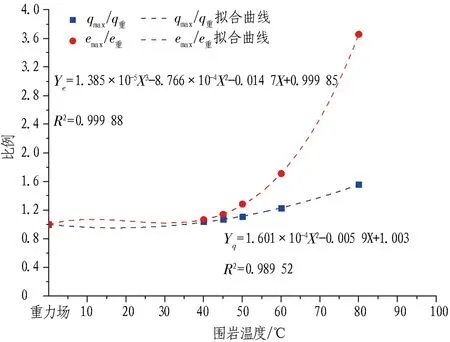
(a) 围岩压力增大比例随围岩温度的变化规律 (b) 侧压力系数随围岩温度的变化规律
图12围岩压力数值计算结果
Fig. 12 Numerical calculation results of pressure
4 荷载模式验证与运用
以高地温隧道荷载计算公式为基础,采用ANSYS有限元软件建立隧道二次衬砌的二维和三维荷载-结构模型,并与现场实测的二次衬砌应力进行对比分析,验证高地温隧道荷载修正公式的适用性,并探究高地温隧道二次衬砌的安全特性。
4.1 模型简介
4.1.1 计算模型及参数
运用ANSYS软件,建立二次衬砌的二维和三维荷载-结构模型。2个模型的相关参数选用桑珠岭隧道的设计参数,二次衬砌材料为C35混凝土和HRB400钢筋。在隧道拱顶、拱肩、拱腰、边墙和墙脚处设置监测点。具体建模和材料信息如表5和表6所示,模型如图13所示。

表5 模型信息

表6 衬砌材料参数
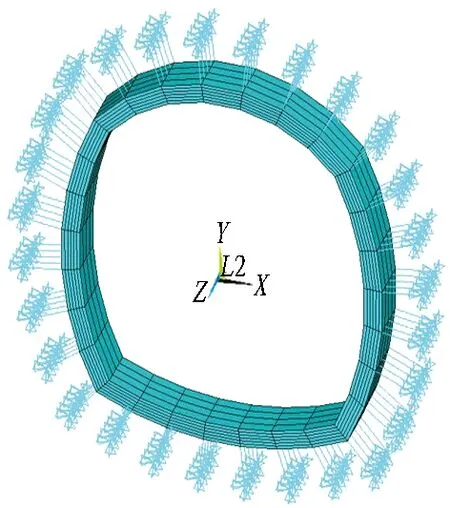
(a)三维荷载-结构计算模型
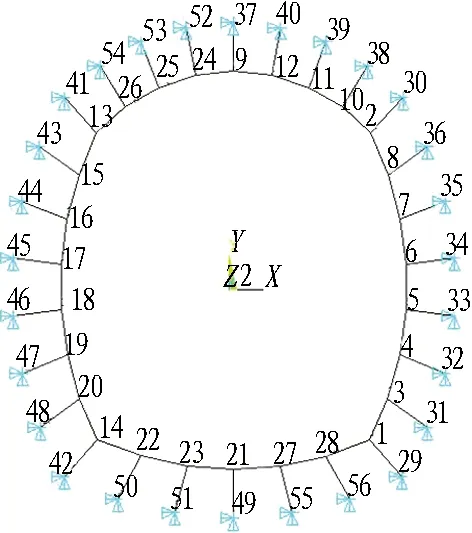
(b)二维荷载-结构计算模型
图13荷载-结构计算模型
Fig. 13 Load-structure calculation model
4.1.2 计算工况
依据文献[11]中的荷载公式和荷载修正公式,共设置6种计算工况,围岩等级设为Ⅴ级,二次衬砌荷载分担比取0.5,具体数值如表7所示。其中,无温度场时的工况通过《铁路隧道设计规范》[15]中公式计算得出,其余温度下的荷载通过荷载修正公式计算得出。各工况下的均布荷载转化为节点荷载后施加于模型节点上。
4.2 荷载模型再验证
现场试验中围岩初始温度为45 ℃,因此将现场试验与工况3的数值计算结果进行对比分析,如图14所示,并归纳总结,得表8。
表7 荷载-结构模型计算工况
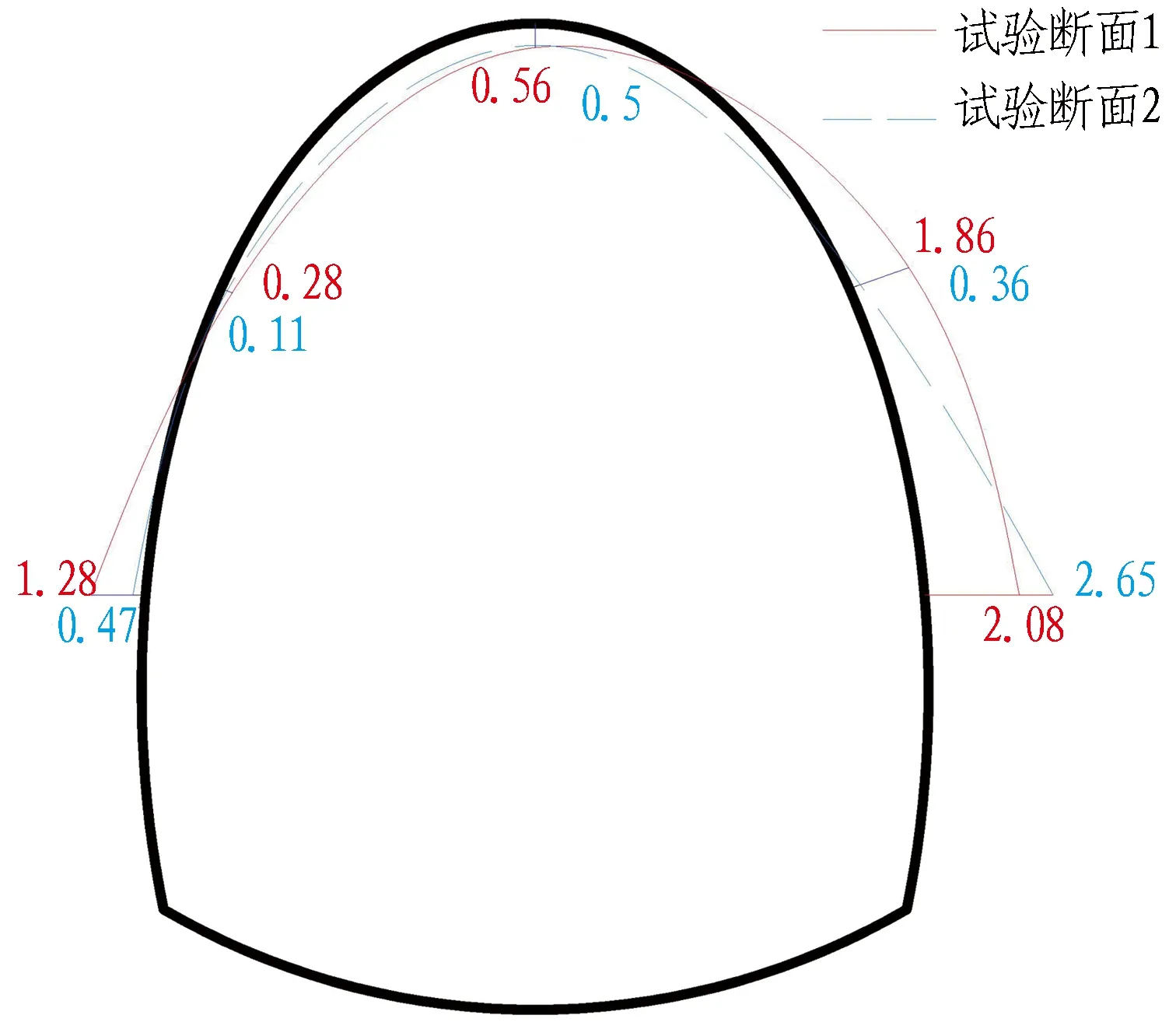
(a) 二次衬砌现场测试外侧应力

(b) 数值模拟外侧应力
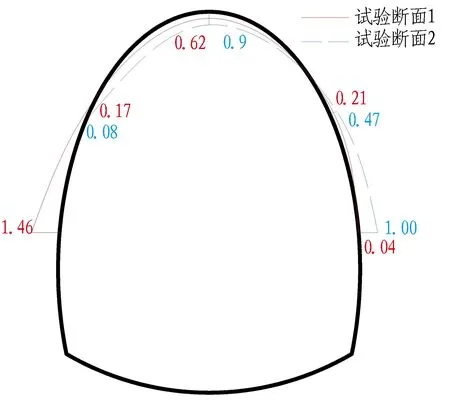
(c) 二次衬砌现场测试内侧应力
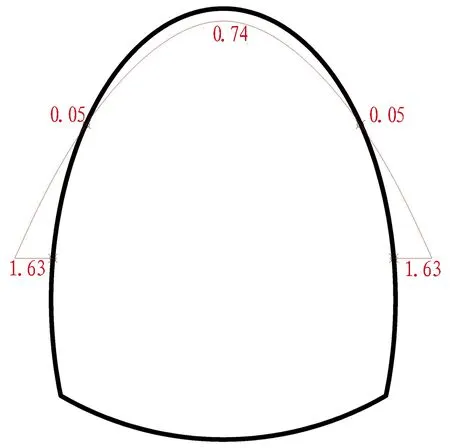
(d) 数值模拟内侧应力
图14二次衬砌应力对比分析(围岩初始温度为45℃)
Fig. 14 Comparison of stress in secondary lining (with initial temperature of surrounding rock of 45 ℃)
表8 二次衬砌现场实测与数值模拟对比
Table 8 Comparison of stress between field test and simulation results

研究方式拉应力分布拉应力max/MPa压应力分布压应力max/MPa对比结果二次衬砌外侧应力现场试验拱腰、拱顶0.56/0.5边墙、拱腰2.08/2.65数值模拟拱顶0.41边墙、拱腰2.00压应力平均偏差14.1%,拉应力平均偏差22%二次衬砌内侧应力现场试验拱腰、拱顶0.62/0.9边墙、拱腰1.46/1.00数值模拟拱腰、拱顶0.74边墙、拱腰1.63压应力平均偏差24.51%,拉应力平均偏差17%
由图14和表8可知: 通过现场试验和数值模拟获得的二次衬砌外侧应力均表现为边墙受压,并且从边墙到拱顶,应力状态逐渐由受压变为受拉; 现场试验所测得的外侧最大压应力分别为2.08 MPa和2.65 MPa,数值计算最大压应力为2 MPa,平均偏差为14.1%,而拱顶的最大拉应力偏差为22%,同时,二次衬砌内侧均表现为边墙受压,拱顶受拉; 2种试验方法测试下的最大压应力偏差为24.51%,最大拉应力偏差为17%。通过对比二次衬砌应力分布和大小可知: 应力分布大致相同,应力大小上存在误差,但相差不大。因此,证明高地温隧道荷载计算公式具有适用性。
4.3 数值计算结果分析
通过分析各工况下数值计算结果,获得隧道二次衬砌在高地温环境下的力学特性。
4.3.1 二次衬砌应力特性分析
通过数值三维荷载-结构模型获得了6种工况下二次衬砌的应力云图,部分云图如图15所示。提取各分析点应力,如图16所示。
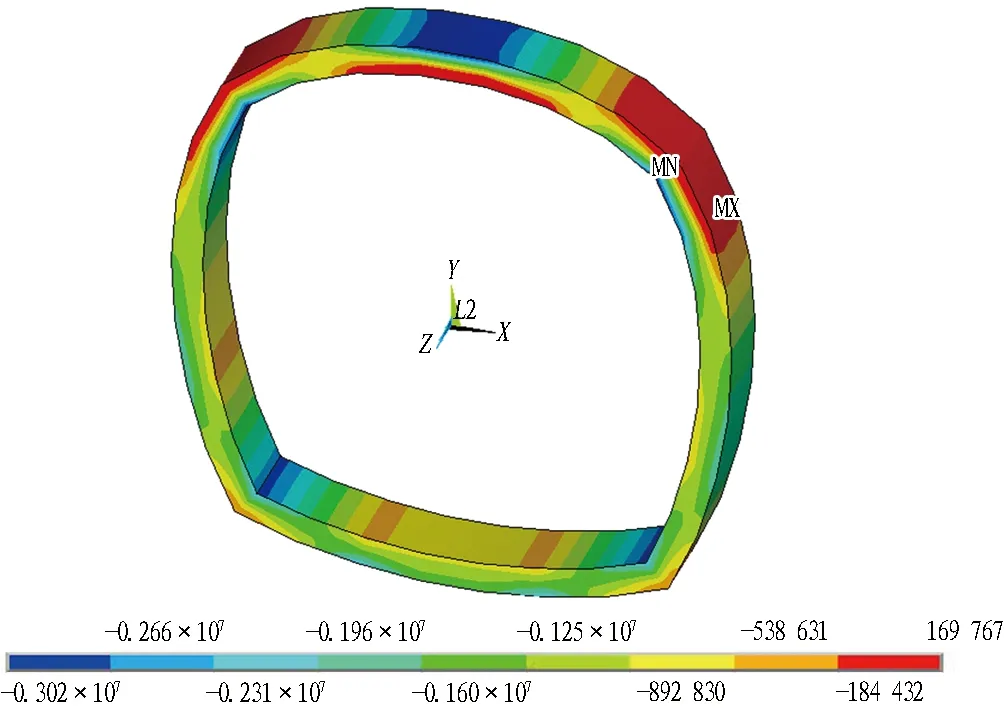
(a) 无温度场
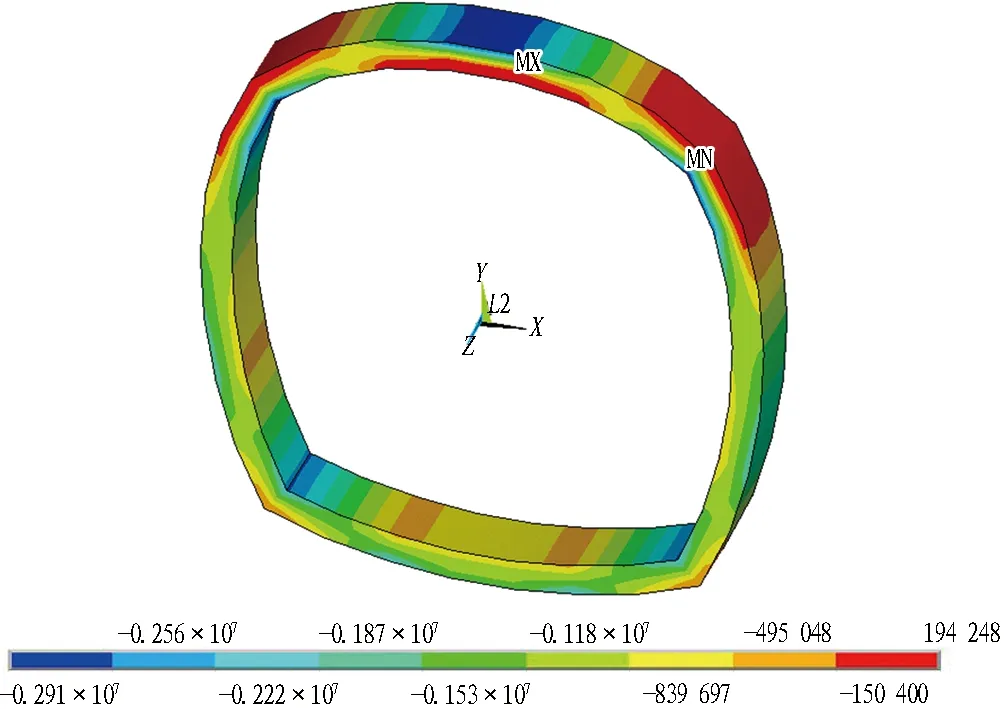
(b) 40 ℃
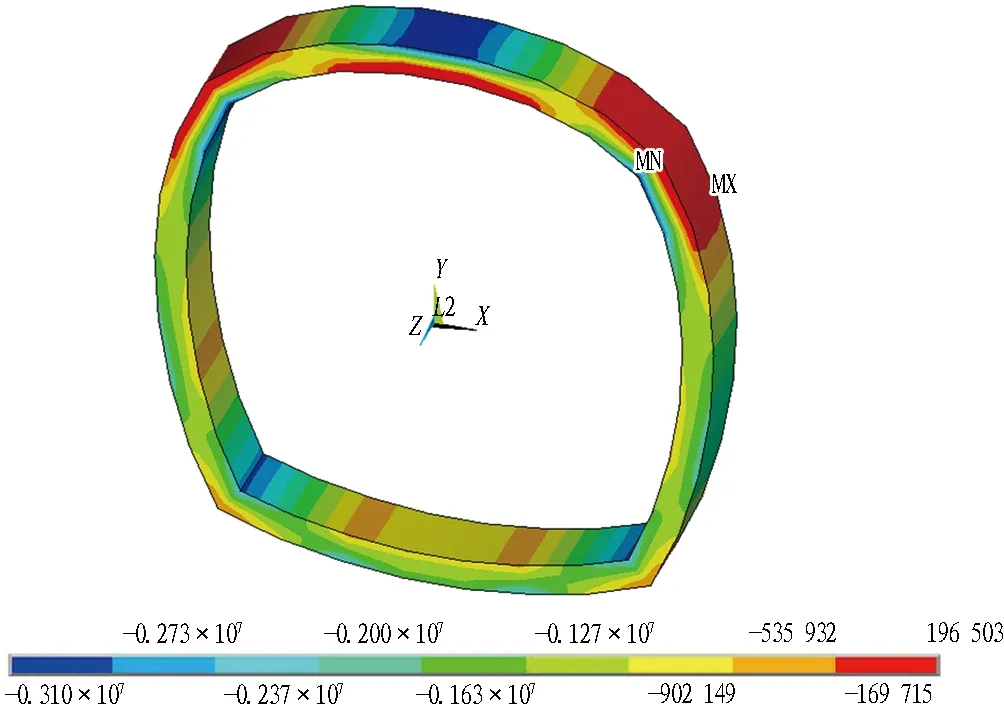
(c) 45 ℃
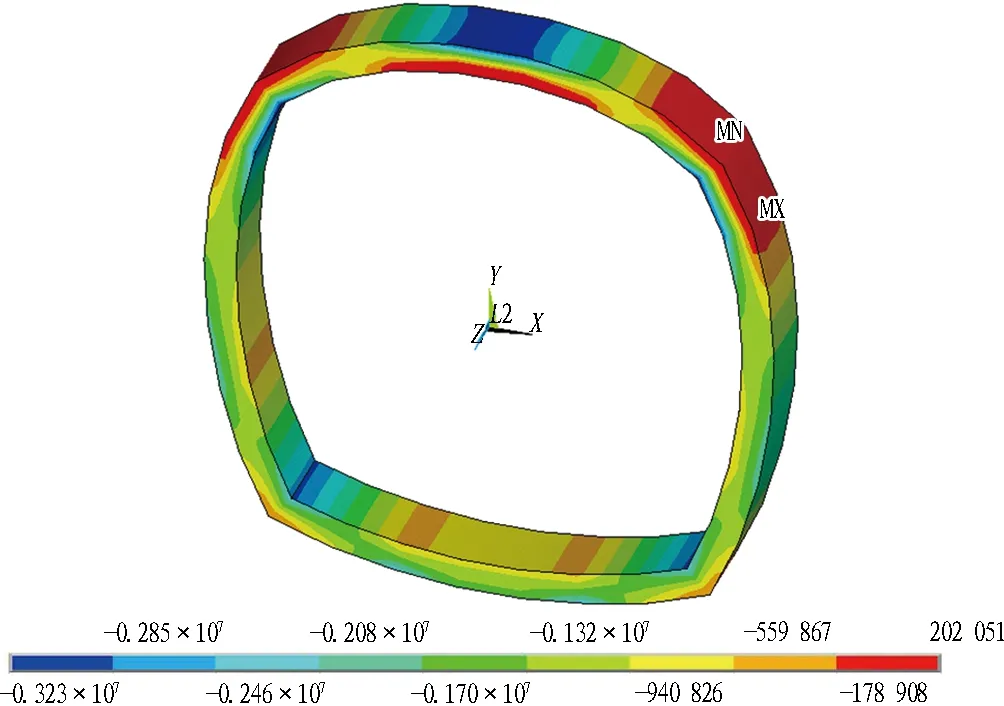
(d) 50 ℃
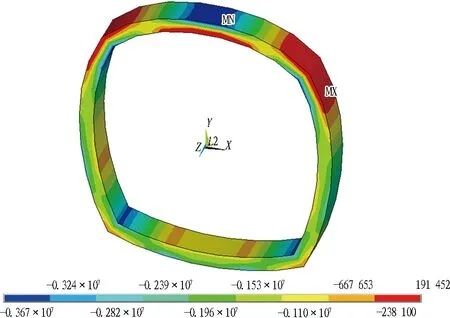
(e) 60 ℃
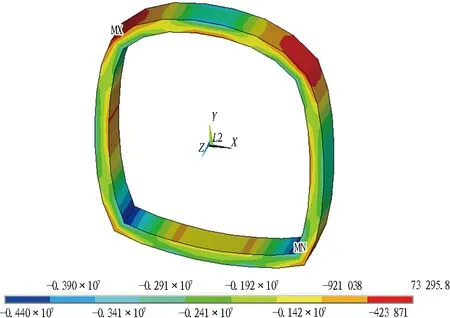
(f)80 ℃
图15各工况下二次衬砌第三主应力云图(单位: Pa)
Fig. 15 Stress nephograms of third principal stress in secondary lining (unit: Pa)
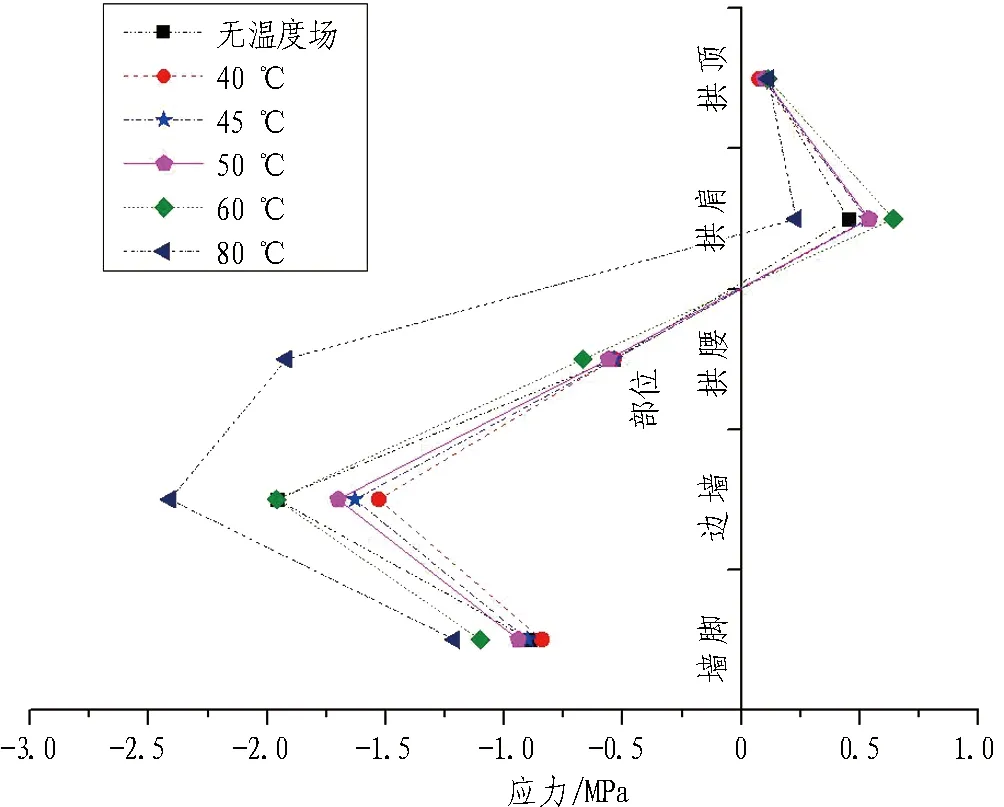
(a) 二次衬砌外侧应力变化曲线
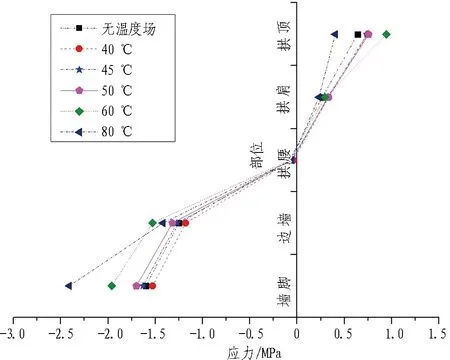
(b) 二次衬砌内侧应力变化曲线
由图16可知: 二次衬砌内外侧在墙脚和边墙处均受压,外侧最大压应力位于边墙,内侧最大压应力位于墙脚; 从墙脚向拱顶的过程中,衬砌结构的应力逐渐由受压变成受拉; 外侧最大拉应力出现在拱肩,而内侧最大拉应力出现在拱顶,且在数值上大于外侧拉应力的最大值; 无温度场的计算工况下衬砌应力较大,原因是无温度场的计算工况中,侧向均布压力系数是依据规范和经验进行选取的,取值较大,因而对计算结果存在一定影响; 从应力随温度变化的角度进行分析,内外侧压应力均随温度升高呈现出增大趋势,但各点增大速率存在一定差异; 拉应力值随温度的增加呈波动增长。
4.3.2 二次衬砌安全特性分析
通过二维荷载-结构模型,获得了各工况下二次衬砌的弯矩和轴力,并计算出各工况下的最小安全系数,同时得出最小安全系数随围岩温度的变化曲线,如图17所示。
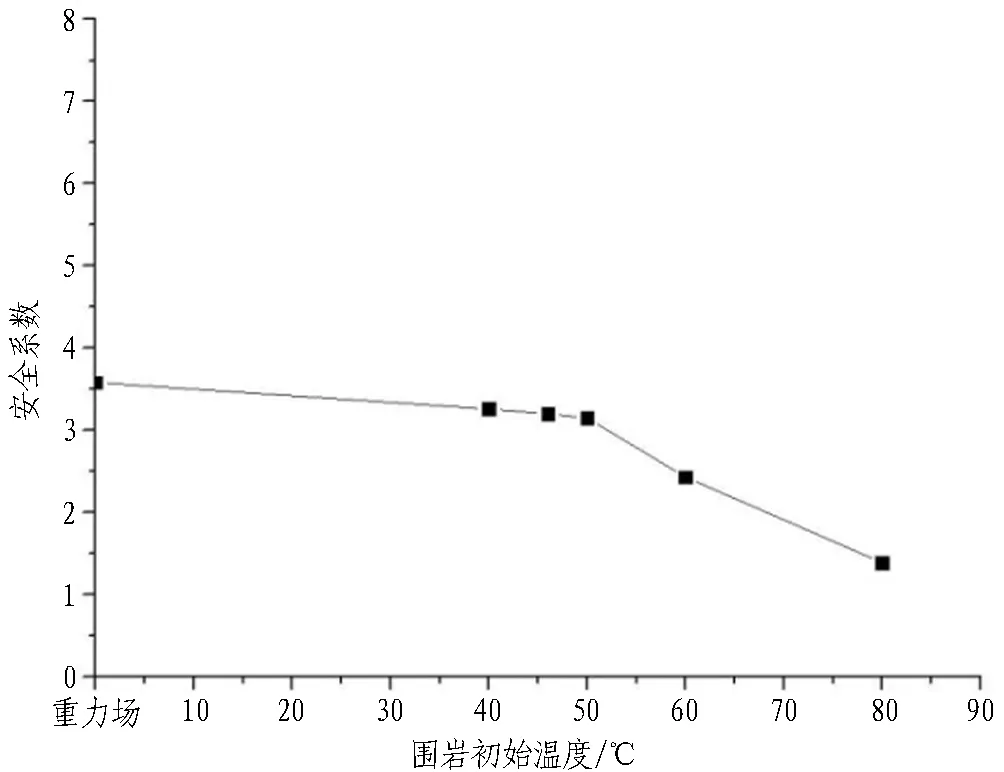
图17 最小安全系数随围岩温度变化曲线
Fig.17 Minimum factor varying with surrounding rock temperature
各工况下的最小安全系数均出现在衬砌拱顶位置,因而在高地温隧道中二次衬砌的拱顶为最不利位置。最小安全系数随围岩温度的升高呈降低趋势,温度小于50 ℃时,降低趋势较缓,温度高于50 ℃时,降幅变大。温度为50 ℃时,最小安全系数为3.15,已非常接近于受拉情况下的最小安全系数。温度为60 ℃时,最小安全系数为2.43,已经无法满足规范要求,存在被破坏的可能性。
4.3.3 二次衬砌裂缝分析
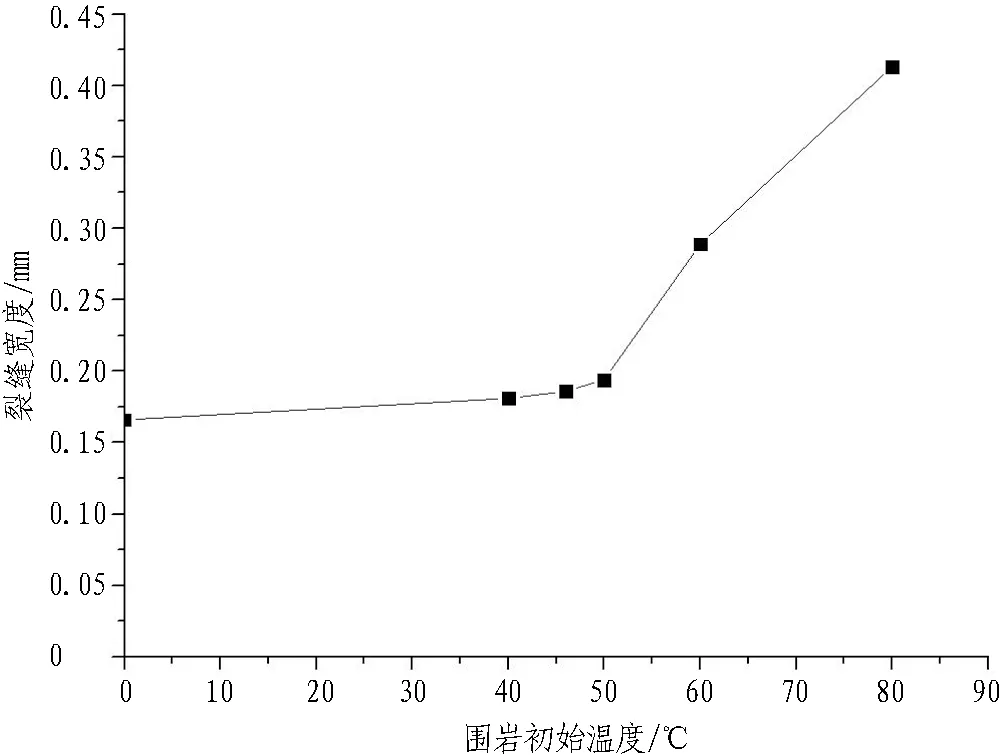
以二维荷载-结构模型中各工况下的轴力和弯矩值为基础,根据《铁路隧道设计规范》[15]中混凝土裂缝计算公式求出衬砌裂缝,各分析点裂缝宽度如图18所示。选取每种工况下最大裂缝宽度,获得最大裂缝宽度随围岩温度变化规律。同时,以无温度场时的裂缝宽度为基准,将其余工况下的裂缝宽度进行量纲一化处理,获得最大裂缝宽度扩大系数随温度的变化规律,如图19所示。
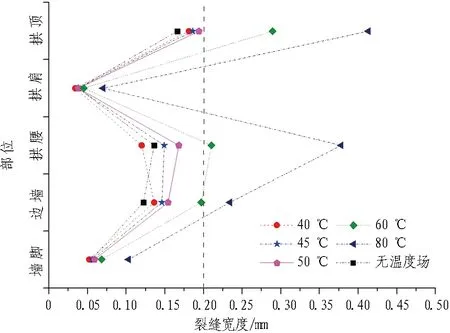
图18 各工况下分析点裂缝宽度
(a) 最大裂缝宽度随温度变化曲线
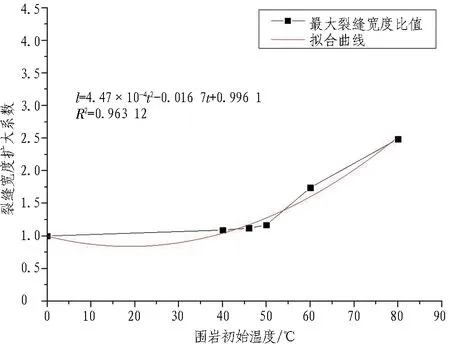
(b) 最大裂缝宽度扩大系数
Fig.19 Maximum crack width varying with surrounding rock temperature
由图18可知: 重力场和围岩温度较低的情况下,最大裂缝出现在拱顶处; 随着温度的升高,当温度达到80 ℃时,拱顶、拱腰和边墙处的裂缝宽度均大于0.2 mm。因此,随着温度的升高,裂缝的分布范围也存在扩大趋势。由图19可知: 随着围岩初始温度的升高,裂缝宽度呈现出增大趋势; 当初始温度小于50 ℃时,裂缝宽度的增幅不明显;当温度大于50 ℃时,裂缝宽度随温度发展的速率变快; 最大裂缝宽度的增大系数可拟合为l=4.47×10-4t2-0.016 7t+0.996 1 (l为高地温隧道裂缝扩大系数;t为围岩初始温度,℃)。
5 结论与讨论
结合桑珠岭隧道现场试验和数值分析,建立了高地温隧道荷载模式,探究了高地温隧道二次衬砌的安全特性,并得出以下结论。
1)高地温隧道二次衬砌应力在10 d内变化较快,20 d后趋于稳定。最大拉应力均位于拱顶处,且内侧最大拉应力大于外侧最大拉应力,而最大压应力常出现在边墙处。
2)建立了高地温隧道荷载计算模型,垂直均布荷载修正系数与水平荷载修正系数均可表示为围岩温度的多项式。
3)二次衬砌内外侧在墙脚和边墙处均受压。从墙脚向拱顶的过程中,衬砌结构的应力逐渐由受压变成受拉。外侧最大拉应力出现在拱肩,而内侧最大拉应力出现在拱顶。内外侧压应力均随温度升高呈现出增大趋势,但各点增大速率存在一定差异。拉应力值随温度的增加呈波动增长。
4)二次衬砌最小安全系数出现在衬砌拱顶位置,最小安全系数随围岩温度的升高而降低。温度小于50 ℃时,降低趋势较缓,温度高于50 ℃时,降幅变大。温度为60 ℃时,最小安全系数为2.43,存在被破坏的可能性。二次衬砌最大裂缝位于拱顶,裂缝宽度随围岩温度的升高而增大。
现场实测数据受施工影响干扰,可能会存在一定误差,同时,实测工况所包括的围岩温度范围还不够广泛,有待更多实测数据对结论和模型进行实际验证。
