基于差分进化电液伺服滑模控制研究
2019-12-13曹昌勇
曹昌勇,林 华,苗 芳
(1.皖西学院 机械与车辆工程学院,安徽 六安 237012;2.辽宁省计量科学研究院,沈阳 110004)
电液伺服系统质量轻,响应快[1],已在许多场合得到应用。同时,系统的参变量多,偶合性强,存在不确定的非线性因素以及干扰问题,针对这些问题,许多学者进行了相关方面的研究。王喆等[2]提出了一种轧机两侧液压伺服位置自抗扰同步控制方法,提高了系统的动态性能和抗干扰能力。韩以伦等[3]利用电液伺服系统设计实现了液压伺服张紧装置,并利用模糊PID参数整定方法实现了装置的高精度控制。李元春等[4]设计了液压机械臂自适应二阶滑模控制律,使系统精确地跟踪期望轨迹并具有较强的鲁棒性。王云鹏等[5],刘艳雄等[6]采用遗传算法实现了PID控制参数的在线整定,加快了伺服缸的响应速度,提高了控制精度。黄山云等[7]以DSP控制器为核心,设计实现了伺服系统的神经网络PID控制,减小了响应的超调量,提高了系统的响应速度。
差分进化算法是一种随机启发式搜索算法,采用实数编码,简单的变异操作和一对一竞争生存策略,降低了遗传操作的复杂性,其性能要优于遗传算法、粒子群算法等进化算法。滑模控制(SMC)的非线性控制表现为控制的不连续性[8],根据系统的当前状态,迫使系统按照预定“滑动模态”轨迹运动,使得控制响应速度快、对参数的变化以及干扰不灵敏,并且具有简单的物理实现。鲁棒控制[9]可很好地控制系统的性能,在一定参数摄动下维持系统的某些特性。
本文分析了电液伺服系统控制数学模型,利用滑模控制原理和一类K型观测器实现系统输出的位置跟踪以及对位置的速度和加速度估计。通过Matlab/Simulink平台设计实现控制算法的连续系统仿真,从而可分析控制算法的稳定性、响应速度和控制精度。
1 电液伺服系统及其控制模型
1.1 伺服缸的位置传递函数
张鑫[10]、冯业恒[11]根据电液伺服系统本身的物理特性以及对外部环境的分析,将伺服阀当作无摩擦和泄漏的四通滑阀,液压缸也处于理想状态,并在工作腔内每处压力相同,液压油温度和容积弹性模量均视为常数,得到伺服缸位置传递函数。
(1)
式中:Y为伺服缸位置传递函数;s为拉普拉斯算子;Kn为传递函数增益;a、b、c、d为s多项式系数;Kq为电液伺服阀的流量增益;Ap为液压缸工作面积;Xv为主控制信号;Kce为总流量压力系数;Vt:为液压缸总容积;βe为液压油弹性模量;F为干扰信号;Mt为折合到活塞杆的总质量;Be为活塞及负载的粘性阻尼系数;K为负载弹性刚度。
由传递函数模型可知,信号的微分获取是控制的关键因素,精确地获取信号的速度对于控制系统至关重要,而根据传感器测量得到信号的速度比较困难,采用K型低增益观测器对信号速度和加速度进行估计是一种可行的方法。
K观测器模型可设计为
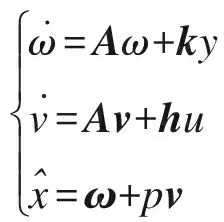
(2)
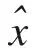
若使A的特征值具有负实部。可使A的特征值全为-10,可得观测器的k1、k2、k3为
(3)
1.2 滑模控制
运用滑模控制时,首先应建立滑模函数,取跟踪误差e,滑模因子c1、c2滑模因子满足Hurwitz条件[12-13],设计滑模函数s为
(4)
式中:x1为系统输出;x1d为系统输入。
滑模控制器输入为
(5)
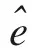
1.3 差分进化算法
差分进化算法通过群体内个体间合作与竞争智能地优化搜索,降低了遗传操作的复杂性,通过多点搜索以大概率找到全局最优解,算法的基本流程包括四个步骤。
初始群体的生成是随机的,其中第i个个体可表示为
(6)
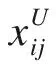
基本变异操作可随机选择3个不相同个体进行如下计算。
hij(t+1)=xp1j(t)+F(xp2j(t)-xp3j(t))
(7)
式中:h为变异后的个体值,i≠p1≠p2≠p3;t为变异代数;F为变异因子。
为了增加群体的多样性,设置交叉概率与交叉算法为:
(8)
式中:v为交叉后的个体值;randlij∈(0,1);P为交叉概率,P∈(0,1)。
交叉操作后要通过评价函数确定xi是否为下一代成员,评价函数需根据具体实际建立,本文根据输入输出误差e,控制器输入u设计评价函数,并采用惩罚函数避免超调,模型如下。
(9)
式中:J为评价函数;ω1、ω2、ω3为权值。
1.4 优化策略与分析
根据式(5)和式(6)可知c1、c2和ks是滑模控制中重要的三个参数。c1、c2决定了滑模函数滑模面的位置,人为设定的滑模面并非最优滑模面,通过优化滑模因子可得到最优滑模面与滑模函数。收敛速率能保证系统指数收敛,适合解决大阶跃响应控制问题。
根据评价函数设计基于差分进化算法的滑模优化控制,以输入输出误差,控制输入作为优化性能指标,滑模因子与收敛速率作为待优化的调节参数,控制输入为平方项的目的是为了防止控制能量过大,对输入输出误差采用惩罚功能,避免超调现象产生,惩罚项的权值要远大于控制输入项权值,保证对超调的惩罚是足够大的,保证控制系统的跟踪精度与控制效果。
2 系统仿真
2.1 仿真程序结构及其算法流程设计
仿真程序的结构设计包括两大模块:滑模控制模块和差分进化模块。其中滑模控制模块使用Matlab/Simulink连续系统完成仿真,得到位置、速度、加速度跟踪信号等,将滑模控制模块作为差分进化模块的子模块进行调用,评价函数作为评价单元集成在差分进化模块中,调用评价函数得到评价数值。评价函数中集成有滑模控制模块,只有滑模控制模块仿真完成后才能得到评价函数所需的评价参数,否则不能进行评价函数的计算。评价函数计算完成后再回到差分进化模块,进入下一次进化操作。
根据式(7)~式(10)进行群体的差分进化操作,在评价函数里首先对滑模控制系统进行仿真,仿真结束后会得到评价函数中需要的评价参数,根据仿真结果计算评价函数值,通过不断地判断评价函数值,不断更新最优解直到得到全局最优解。
滑模控制模块是完成系统控制仿真的核心模块,如图1所示。其中Signal、MSystem_ctrl、SFG_plant、K_levant均为S-Function写成的连续系统,Signal是信号生成部分,仿真生成sin(πt)正弦信号。SFG_plant是系统模型,K_levant是K型观测器,用于对从系统模型输出的信号进行观测和估计,MSystem_ctrl是控制器部分,输入激励信号与观测器观测的信号,采用式(5)建立的滑模控制模型对系统进行控制,实验设置仿真时间为2.5s。变量BsS用于存储每次迭代时所需的待优化参数;变量ut用于存储控制输入;变量y用于存储输入信号、输出信号和观测信号及其速度、加速度。
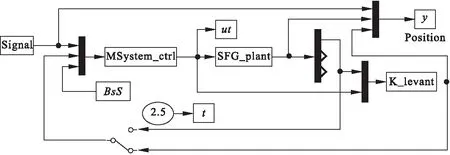
图1 Simulink 滑模控制模型
2.2 仿真参数设置与结果分析
取定常力的线性定常控制系统模型:a=1,b=0.4,c= 24336,d=0,Kn=15948000。根据式(3)可得k1=29.6,k2=-24048,k3=-709730。差分进化待优化参数设置:c1∈(5,600),c2∈(5,600),ks∈(20,2000),变异因子F=1.2,交叉概率P=0.75,设置进化代数为50,染色体大小为30个,待优化参数为3个,根据式(10)对每一代的进化进行评价,最终得到最优解。
根据仿真参数设置得到最优函数变化情况,如图2所示。可知优化指标在第30次迭代之前就进入了稳态区,说明此时已经找到了全局最优解,30次迭代之后,优化指标已基本稳定。通过图3亦可看出,待优化参数在30次迭代时已基本不变。

图2 优化指标变化曲线
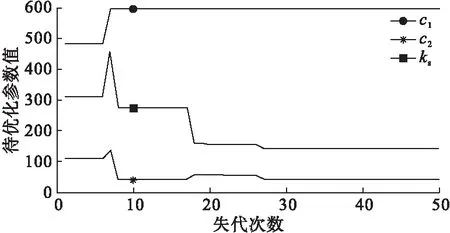
图3 待优化参数变化
经过50次迭代后得到最优解为c1=600,c2=45.931,ks=143.15,最优指标为J=1.4672,可见最优指标数值非常小,说明系统对输入信号的跟踪非常精确,通过比较跟踪曲线和输入信号曲线可进一步更直观地分析。
由于迭代在30次时已进入稳态,为保证对比的区别性,取5个不同迭代次数的跟踪曲线,选择第1、7、10、22、50次迭代时的跟踪曲线,与理想的输入曲线进行对比,如图4所示。
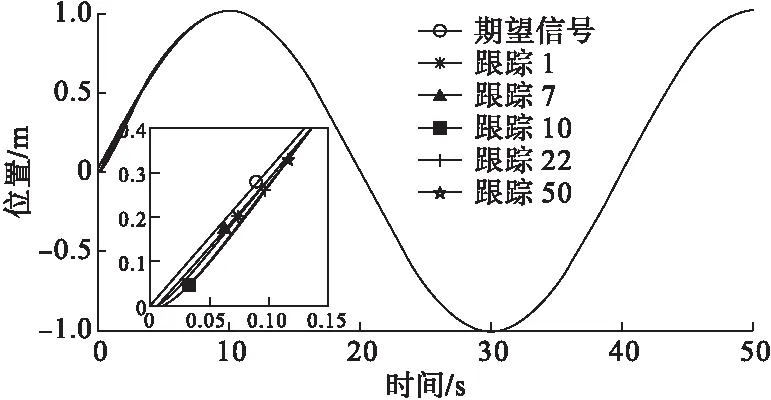
图4 位置跟踪曲线
由图4可知,各迭代次数对应的位置跟踪曲线最终都能精确地收敛于理想位置曲线,第50次迭代跟踪曲线在初始跟踪时跟踪速度较慢,当随着时间的推移,其跟踪速度逐渐增大,且更快地达到理想位置。由于增加了误差惩罚项,故每次迭代后的位置跟踪曲线没有发生超调现象,均小于或等于理想曲线对应值。
比较误差变化曲线,分析各迭代次数对应的误差大小以及收敛速度,如图5所示。根据控制输入曲线分析控制输入能量的大小,输入能量越小越好,如图6所示。根据图5可知随着迭代的不断进行,待优化参数不断得到优化,位置误差的收敛速度不断增大;结合图6可知控制输入非常小,在0.001 m级别,相对误差较小;结合图2可得第50次迭代,即差分进化进入稳态后,位置误差和控制输入达到最优水平,此时的优化函数J的数值最小。
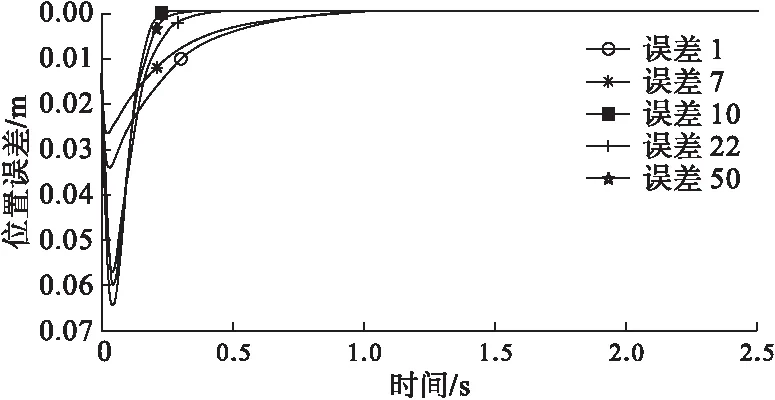
图5 误差收敛曲线
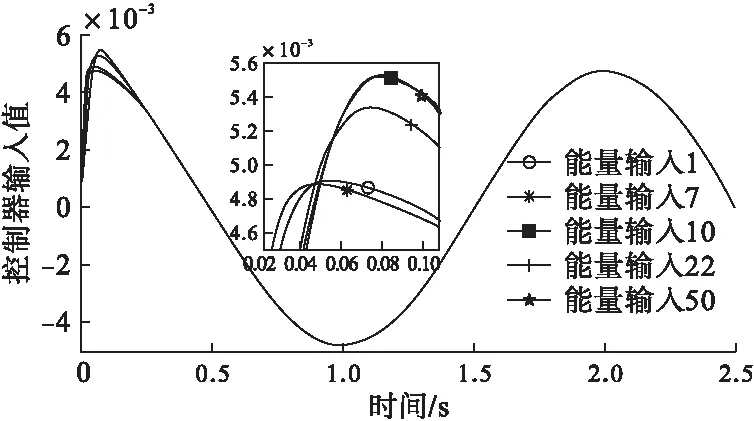
图6 控制输入
使用优化后的参数进行速度跟踪的分析,如图7所示。可知系统在0.3s左右既能精确跟踪理想速度曲线,速度跟踪曲线与速度观测曲线几乎完全重合,说明观测器对系统输出的观测是非常精确的;结合图4位置跟踪曲线可知,优化后的控制器具有收敛速度更快、位置误差与控制输入综合性能最优、速度跟踪精确等特点。综合分析可知,运用差分进化算法并结合滑模控制理论,达到了更加精确跟踪的目的,同时又控制输入能量保持在非常低的水平。
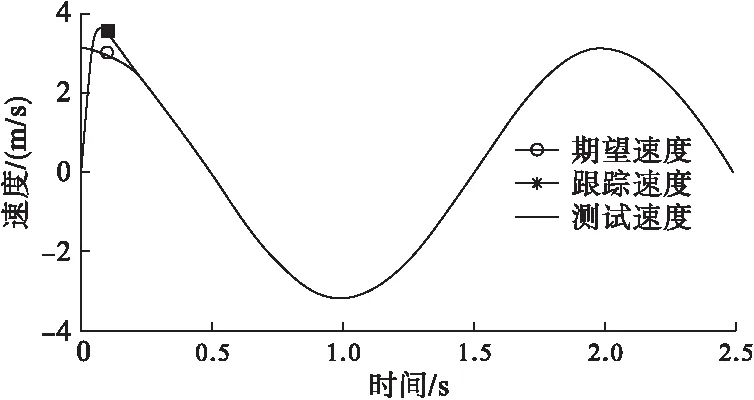
图7 速度跟踪曲线
3 结论
基于差分进化算法和伺服系统滑模控制理论,应用于电液伺服控制。在进行50次进化迭代后得到最优滑模因子与收敛率,仿真结果表明优化后的系统的收敛速度更快,跟踪精度更高,评价指标最低。应用差分进化算法优化滑模控制中的参数,可事先预知系统的跟踪性能并优化跟踪性能,具有很好的实际工程应用意义。
