基于引力模型的中小型城市铁路客运站选址研究

翁雨琳

（西南交通大学交通运输与物流学院 硕士研究生，四川 成都 611756）

0 引言

近年来我国的城市发展迅速，截至2017年年底，我国的城镇化率达到了58.52%，中小城市数量和规模的快速增长是其重要动因。中小城市直接影响和辐射的区域行政区面积达881万km2，占国土面积的91.7%；总人口达10.18亿，占全国总人口的73.23%。中小城市的发展迅速，行政面积广阔，但是与中小城市配套的铁路客运站数量少，且其服务范围远不能覆盖行政区域内的所有人口。 中小城市的铁路客运站的选址较大型枢纽客运站来说，选址范围更小，受既有铁路客运站和铁路线路走行方向的影响大。但中小城市的铁路客运站是联系同级城市之间，以及和大城市之间的重要节点，其选址布局的合理性关系到整个城市的未来发展，铁路系统的运输效率，居民的出行方式及特征。中小城市的铁路客运站选址布局不能直接使用大型铁路枢纽客运站的选址布局方法，需重新审视中小城市铁路客运站的服务对象和服务范围，研究适合中小城市的铁路客运站选址布局的方法。

目前对于铁路客运站选址的研究成果丰富。在定性分析客运站选址问题方面：文献[1-2]选取不同的评价指标，分别采取熵值法、集对分析法对铁路客运站选址问题进行研究；文献[3-4]分别研究了客运专线引入铁路枢纽后，郑州、宝鸡枢纽内的客运站选址方案。在定量分析客运站选址问题方面：文献[5]对客运站布局的集中和分散两种模式分别建立以最小运营支出和固定支出为目标的优化模型；文献[6-7]研究了铁路客运站选址与分工的协同优化问题，着重于枢纽内客运站的选址布局；文献[8]研究了在客运专线条件下，基于旅客选择行为的铁路客运站选址问题；文献[9]构建客流量最大与综合交通成本最小的双层规划模型，来研究城市轨道交通车站的选址问题；文献[10-11]充分研究了火车站的功能，并认为其是铁路客运站选址规划的重要基础；文献[12]应用了Bertolini的模型，研究了瑞士多个火车站，以此为基础研究了选址问题。文献[13]以时间和费用与枢纽选址的关联为基础建立整数规划模型，求取选址地点。综上所述，在对铁路客运站选址方面的研究多集中于大型枢纽内的客运站选址，缺乏对中小城市客运站选址的研究；在研究方法上，无论是多站选址还是选址分工同步优化，都多从铁路投资运营费用方面考虑，缺乏从旅客的角度出发，考虑铁路客运站最大程度吸引旅客客源的研究。

本文从中小城市的发展需求和实际特征出发，考虑其运输组织过程、服务对象、服务范围的特殊性，更多地从旅客的角度出发，考虑铁路客运站对旅客的吸引程度，旅客实际出行费用；也从铁路的角度出发，考虑用地、拆迁以及初始建设投资，多城市联合选址全面，覆盖区域内所有出行小区。建立了系统最大引力模型和系统最小费用模型，设定方案评价函数和偏差指数，对双目标整数规划模型综合优化求解，得到区域内客运站选址方案以及客流集散点分配方案。

1 中小型城市铁路客运站选址目标分析

我国的中小城市大多处于生长阶段，城乡联系不够紧密，旅客出行小区分散，且地级市以下的县城通常不能保证“一城一站”，已有铁路客运站的服务人群也多数分布在铁路客运站所在的城市范围内，对乡镇居民以及临近无铁路客运站城市的居民吸引度较低。中小城市的铁路客运站需要服务的面积广，其服务范围内旅客的出行方式中铁路出行的占比较低。因此为满足中小城市中旅客的出行需求，最大程度地吸引城区内及周边乡镇地区的客流，应满足以下几个目标：

1）城乡客运一体化发展。新建铁路客运站应远离既有客运站，有意识地让客运站带动城乡客运的一体化发展，更多地服务于市区周围、乡镇地区的旅客。

2）加强与周边城市之间的联系强度。对于不能保证“一城一站”的城市，可将几个临近的城市划为一个区域进行联合选址，令其辐射的服务范围最大化。

3）改变旅客的出行模式。新建的铁路客运站应对乡镇的客运提供一定份额的交通出行保障，改变其传统的出行模式，吸引更多的铁路出行客流量。

4）满足城市、城镇的未来发展需求。在中小城市的未来交通出行中，随着铁路客运站对旅客的吸引程度不断增大，铁路出行方式所占的比重也将增大，客运站的选址布局还应充分考虑未来客运量的增长需求。

2 模型建立

2.1 最大系统引力模型

中小型城市客运出行的目标人群应包括城镇以及乡村居民，要特别涵盖各个行政区域交界区的偏远人群。而在中小城市的出行中，由于地貌距离的限制，旅客的出行方式中铁路的占比较少，在对其进行选址时应充分考虑铁路客运站对于旅客的吸引程度。且铁路客运站对乘客的吸引程度存在“规模效应”和“递远递减”现象。因此，本文通过系统引力模型，根据铁路客运站对出行小区吸引力大小，将出行小区划分给对其吸引力最大的客运站[14]，构建铁路客运站的引力模型，以系统引力最大化来优化铁路客运站点的选址和服务范围。

假设区域内有出行小区集合I，铁路客运站集合J，以Qj表示铁路客运站的质量，即表征该铁路客运站的竞争力，用该客运站的规模Bi、所在区位的交通便利程度Ci、所在区位的经济发达程度Di来对其竞争力进行衡量，并对Bi，Ci，Di进行归一化处理，则Qj的表达式为：

则衡量铁路客运站对出行小区的吸引力Z1的表达式为：

式中：Qi为出行小区的“质量”，用出行小区的人口衡量；a1，a2，a3为权重系数，且a1+a2+a3=1；λ 为吸引力系数；k为设定的铁路客运站数量；dij为铁路客运站与出行小区之间欧式距离；θ为引力衰减指数，一般取[1,2]；fj为0-1变量，如果铁路客运站被选中取1，否则取0；yij为如果客流集散点i由客运站j服务取1，否则取 0。

约束（3）表示总共建设K个客运站；约束（4）和（5）表示客流集散点只能分配给已选中的客运站，且只能分配给一个客运站。

2.2 最小系统费用模型

由最大系统引力模型可知，当铁路客运站对旅客的吸引程度越高时，客运站的基础投资费用越高。对于中小城市来说，其能够负担的客运站投资费用十分有限，因此考虑到铁路方面的经济效益，为约束初始建设的投资，建立最小系统费用模型。为了使该模型的优化结果更加贴合实际情况，该模型包括铁路的初始建设投资、运营维护费用以及旅客实际出行费用，是整个系统的费用模型。将旅客出行小区抽象为一个具体的客流集散点，铁路客运站与客流集散点的距离示意图如图1所示。

图1 客运站与客流聚集点距离示意图

衡量系统费用Z2的表达式为：

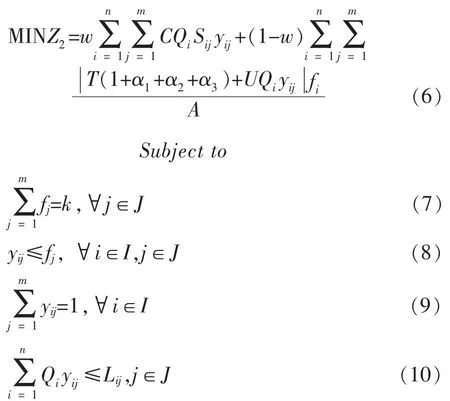
式中：C为单位距离下的单位出行费用；T为客运站基础建设费用；U为日常单位客流量的运营维护费用；Sij为实际路网距离；Lj为铁路客运站能输送的最大客流量；w为权重系数；α1，α2，α3为铁路客运站的征地、拆迁、建设附加费用系数。

目标函数（6）表示旅客实际出行费用，初始建设投资费用，基于客流量的日常运营维护费用。

约束（7）～（9）同约束（3）～（5）。 约束（10）表示，每个客运站的客流量小于等于其所能承担的最大客流量。

2.3 方案评价模型

对上述两个模型分别求解可以得到不同的选址方案，不同的选址方案分别从旅客利益和铁路利益的角度出发。为了最大程度地兼顾到两方面的利益，建立方案评价模型，对其进行优化求解。

目标函数（3）的最优解为Emax，最终选址方案中所得的系统引力与其偏差值为目标函数（7）的最优解为Fmin，最终选址方案中所得的系统费用与其偏差值为d-2、d+2， 由此建立方案评价模型为：

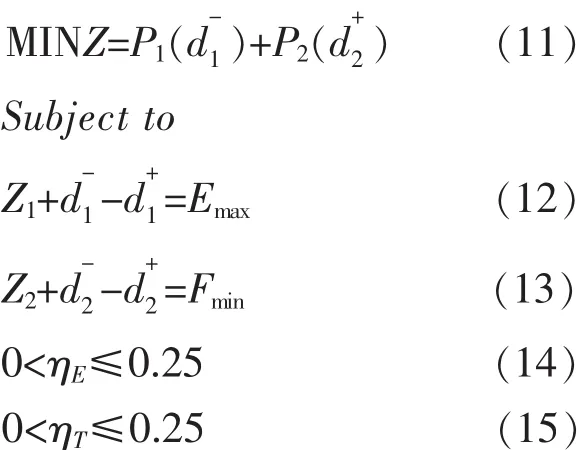
式中：P1为第一目标优先因子；P2为第二目标优先因子；Emax为系统引力最大值；为未达到和超出Emax的正偏差量和负偏差量；Fmin为系统总费用最小值；为未达到和超出F的正偏

min差量和负偏差量；ηE、ηT为偏差指数。

其中，ηE为引力偏差指数，当ηE=0时，系统的引力值达到了最大值，此时为系统引力最优的情况。当0＜ηE≤0.25时，系统的引力值为可接受值。当0.25＜ηE时，认为铁路客运站对旅客的吸引力过小，旅客的出行利益牺牲过多，基本不会选择铁路出行。

其中，ηT为费用偏差指数，当ηT=0时，系统费用达到最小值，此时为系统费用最优的情况。0＜ηT≤0.25时，系统费用为可接受值。当0.25＜ηT时，认为系统费用过大，政府、铁路局无法协调用地，也无法承担初始投资费用。

因此在对目标函数（11）优化求解时还应控制ηE、ηT的值在可接受范围内，即满足约束（14）和（15）。

如图2所示，线段ET即为可接受解的范围。

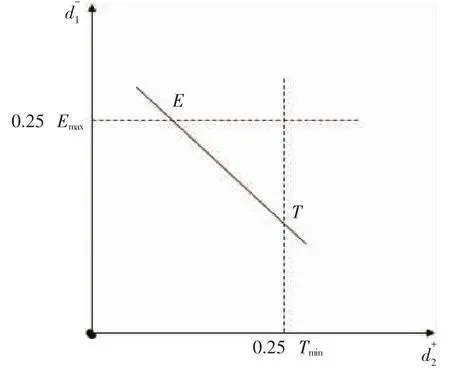
图2 目标函数偏差分析图

3 优化模型

本文建立了双目标规划模型，在满足所有约束条件下，分别求出两个目标的最优解，最后利用方案评价模型以及偏差指数的约束求出最优客运站选址方案。模型优化步骤如图3所示。

图3 模型优化步骤图

步骤1区域内存在m个铁路客运站 （包含既有既有铁路客运站m1个），在最大系统引力模型下，利用目标函数（2），求解客运站个数k=m1到k=m的不同取值下，不同的客运站选址方案以及客流集散点的分配，此时目标函数最优解为Emax。

步骤2在最小系统费用模型下，利用目标函数（6），求解客运站个数k=m1到k=m的不同取值下，不同的客运站选址方案以及客流集散点的分配，此时目标函数的最优解为Fmin，并得到在满足客运需求前提下，最小新建客运站个数。

步骤3根据实际情况确定ηE、ηT的取值范围，为方案评价模型的约束条件。

步骤4 在方案评价模型下，利用目标函数（11），求解在系统引力偏差和系统费用偏差最小的情况下的最优选址方案，以及客流集散点的分配方案。

4 算例分析

4.1 问题描述

假设某区域包含3个相邻的县城，有规划中的新建铁路线从该区域穿过，并规划在该区域新建铁路客运站。该区域东西长100 km，南北长90 km，地形以平原和小型丘陵地带为主，该区域有一个既有铁路客运站，坐标为（60，60）。在实地考察当地的土地使用、自然环境，并收集行政区划分路网构成等相关资料后，将该区域划分为30个出行小区，并将每个出行小区的中心点作为客流集散点[15]。该区域的初始选址方案包含1个既有铁路客运站和7个备选站址。各客流集散点和铁路客运站的位置如图4所示。

图4 客流集散点与客运站平面位置图

计算铁路客运站对各个客流集散点的吸引力，θ 取 1.5，不失一般性地，λ 取 1。Bi，Ci，Di的取值如表1所示。

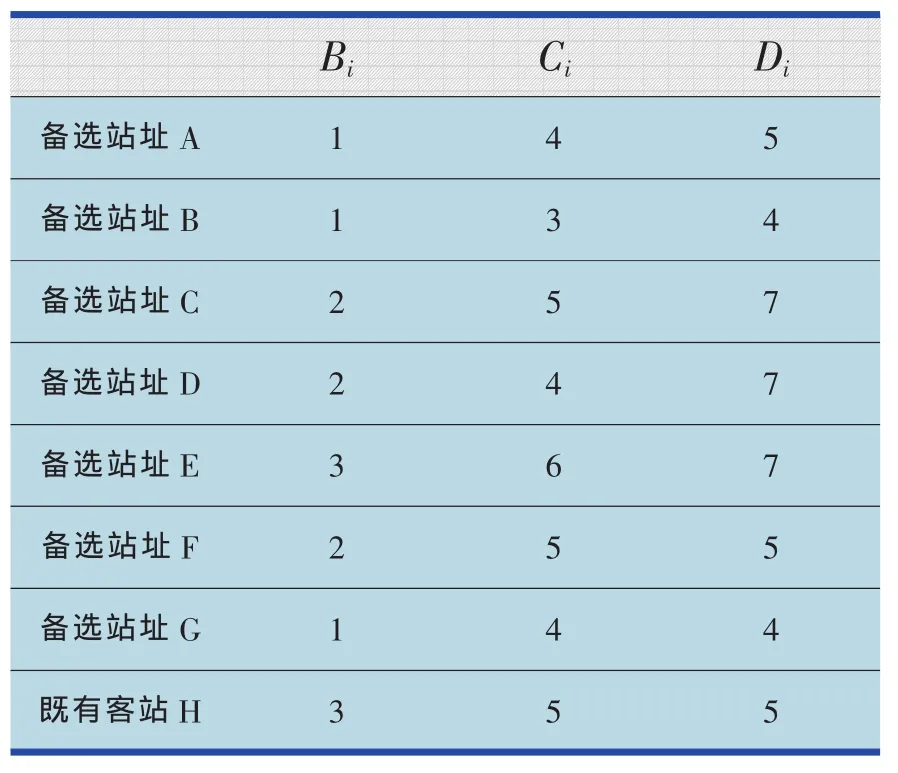
表1 各备选客运站址质量的评价指标

30个客流集散点的坐标及客流量如表2所示,客运站的坐标、最大容量以及附加费用系数如表3所示，各客流集散点到铁路客运站的路网距离如表4所示。其中C取0.72元，U取0.186元，A取10年，T取500 000元。

表2 客流集散点平面坐标及年度客流量表

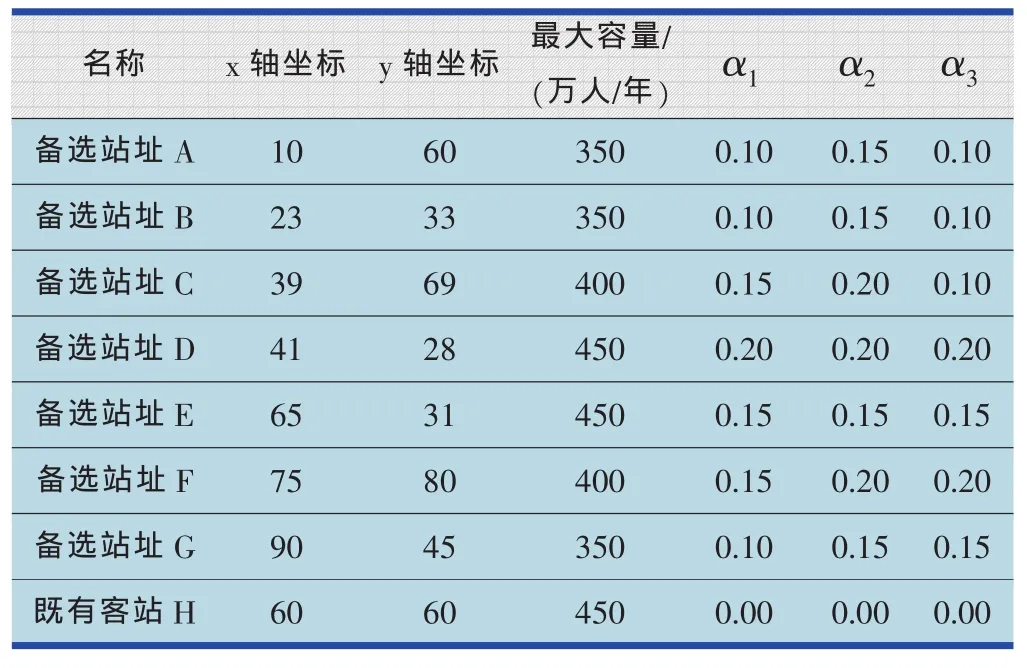
表3 铁路客运站平面坐标、最大容量及附加费用系数表

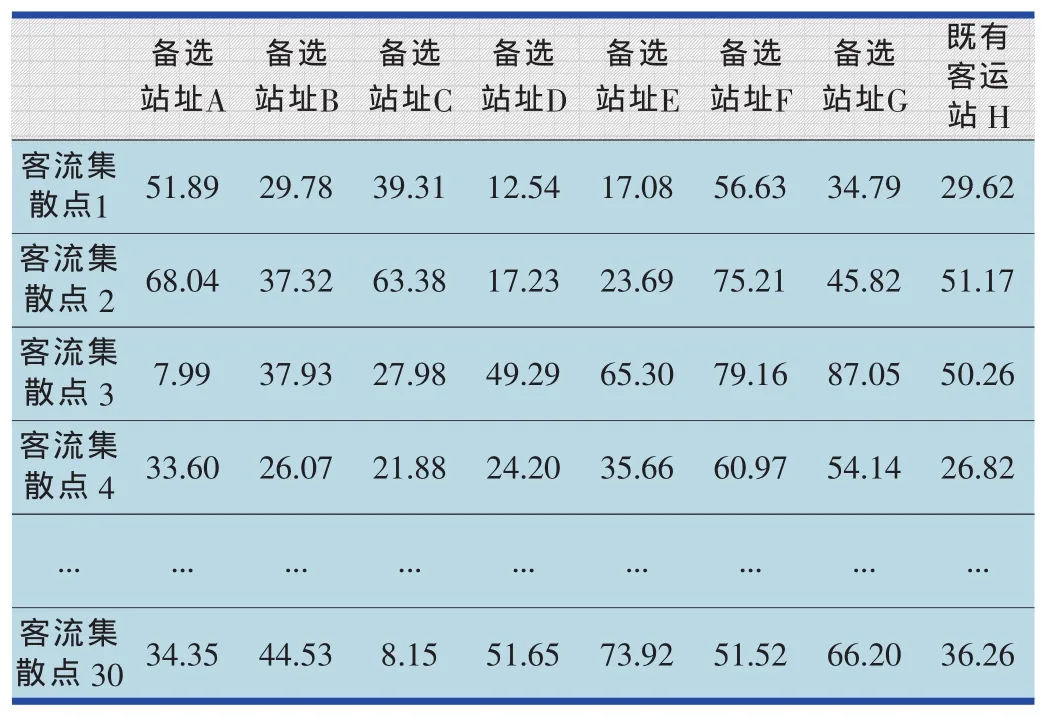
表4 客流集散点到铁路客运站路网距离

4.2 求解结果

本算例中区域内存在7个备选站址和1个既有客运站，求解最优选址方案，包括客流集散点分配以及目标函数最优值。

步骤1对最大系统引力模型优化求解，得到系统引力值随客运站数量的变化趋势。

在客运站数量为3时，客运站选址方案及客流集散点分配方案如表5所示。

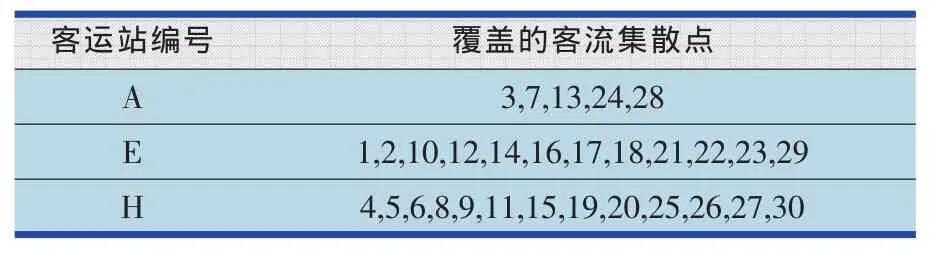
表5 客运站选址方案及客流集散点分配方案

步骤2对最小系统费用模型优化求解，区域内客运站数量至少为3时，可满足客运需求，得到系统费用值随客运站数量变化趋势。

在客运站数量为3时，客运站选址方案及客流集散点分配方案如表6所示。

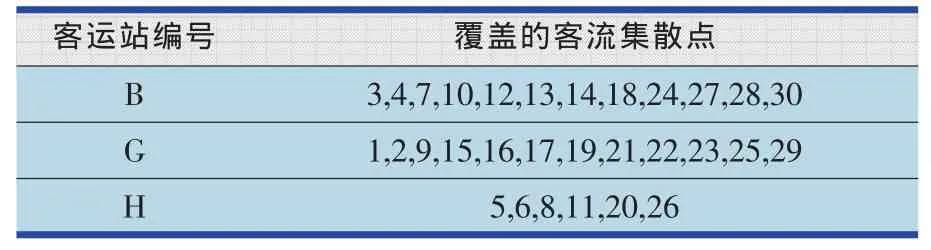
表6 客运站选址方案及客流集散点分配方案

步骤3在客运站数量取值为3的情况下，优化方案评价模型。此时，Emax=5.022,Tmin=2 034 030，设定 ηE、ηT的取值范围为[0，0.25]。 最终铁路客运站选址方案和客流集散点如图5所示。此时的系统引力为Z1=4.380，系统费用为Z2=2 075 250，由此计算引力偏差指数ηE=0.13≤0.25，费用偏差指数ηT=0.02≤0.25，则系统引力与系统费用都在满意解的范围内，该选址方案为最优选址方案。

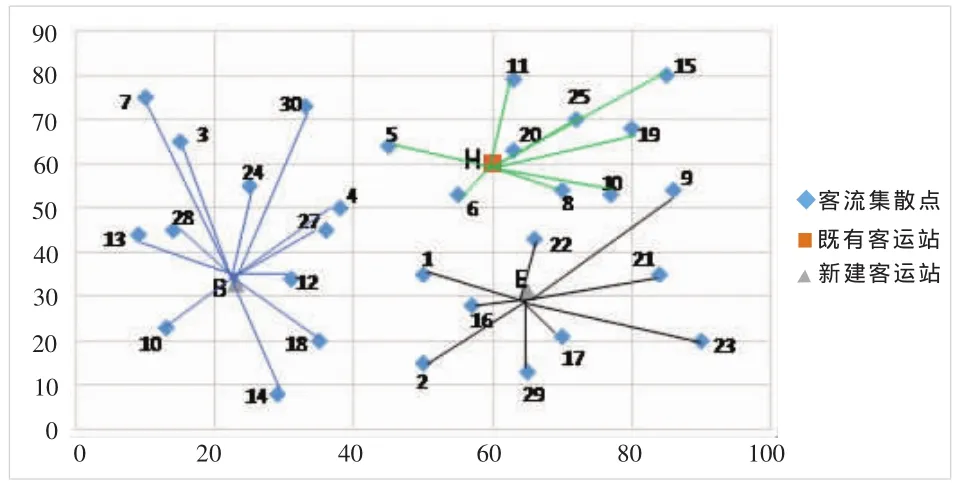
图5 客运站选址方案图

步骤4最终得到的铁路客运站选址方案及客流集散点分配方案如表7所示。

表7 客运站选址方案及客流集散点分配方案

5 结束语

本文基于中小城市客运站的服务范围、服务对象、选址目标等特征，建立了铁路客运站选址的双目标优化模型，并给出了相应算法。从算例分析中可以看出，优化后的客运站选址方案在系统总费用较低的情况下，较好地满足了客运需求，同时又保证了尽量大的旅客吸引力，可以为中小城市的铁路客运站选址提供理论支持，该模型具有其合理性和实用性。