中文文献关键词分布特性研究
2019-12-12冶忠林赵海兴杨燕琳
孟 磊 冶忠林 赵海兴,4* 杨燕琳
1(青海师范大学计算机学院 青海 西宁 810016)2(青海省藏文信息处理与机器翻译重点实验室 青海 西宁 810008)3(藏文信息处理教育部重点实验室 青海 西宁 810008)4(陕西师范大学计算机科学学院 陕西 西安 710062)
0 引 言
近年来,如何根据文献中的一些字词的分布特征,去更好地了解语言的发展、各个学科领域之间的关系、知识扩散和科研话题成为一个热门研究方向,而其中最常用的方法为Zipf定律。例如,刘宇凡等[1]通过分析唐代以来汉语文学中字频的分布,发现了在每个不同的历史时期汉字的使用存在差异,但在比较相近时期汉字的使用习惯是基本一致的;曹盼盼等[2]建立写信间隔时间漂移幂律分布模型,说明了人类书信时间既服从Zipf定律又满足幂律分布;郑亚斌等[3]通过用自然语言处理对歌词做了一些相关实验,验证了歌词分布基本符合Zipf定律;刘胜久等[4]提出了网络信息计量学可能存在Zipf定律的猜想,并通过实验结果很好地证明了此猜想。
目前,针对自动文本摘要生成的研究已经取得了巨大的成功[5],而基于这些成熟的摘要生成算法,构建文本的关键词也是较为容易的。因此,研究如何生成文本(如,科研论文)的摘要或者关键词的理论体系和工程框架已经成熟,但是,针对构建出来的关键词的特性的研究成果却较为少见。
关键词作为表述论文的中心内容有实质意义的代表词汇,既反映了研究成果的核心内容,又揭示了科研内容之间的内在联系、学术研究的方向,更为检索提供了重要手段。同时,关键词分析是研究文献计量学的重要手段,关键词分析是通过将文献著作中的众多影响因素联合分析,客观评价文献和相关学者的学术水平,预测热点研究趋势[6-7]。
本文主要研究中文文献中关键词在不同学科内的分布特性。为了实现该研究目标,可将本文研究的具体细节归纳为三个方面。
首先,本文将关键词分类,即在本文中主要研究三个领域内(人工智能、生物、财经)的关键词在不同搜索引擎中搜索结果数和排名分布特性;其次,在百度学术中爬取三个领域内的关键词,分析每个关键词近三年(2018年、2017年、2016年)的搜索结果数和排名在各自的领域内是否符合Zipf定律,并归纳不同科学领域在不同年份内的Zipf参数规律;最后,为了研究关键词和相关学者之间的关系,本文又构建了关键词-相关学者超网络模型,并基于该超网络模型对一些指标进行了衡量,归纳总结了关键词-相关学者超网络模型的一些特性。
本文主要对以上三个方面展开研究工作,且本文的研究成果可提供一些有趣的结论,对于研究关键词分布特征特性提供了理论支撑和数据支持。
1 相关工作
目前,针对引文网络的研究主要是基于普通的点边网络进行研究。例如,Kajikawa等[8]采用引文网络分析的方法,对能源研究中的新兴研究领域进行了跟踪研究,证实了燃料电池和太阳能电池在能源研究领域正在迅速发展;肖雪等[9]对每个领域的知识研究进展、关键词的分布、主题功能的分析,对引文网络的社团划分进展进行综述性研究;陈云伟[10]通过引文网络演化结构特征等的分析对新方法、新领域和新应用进行了解读;White等[11]通过对引文网络中的合作者之间的通讯方式及社会距离的分析,解释了合作在科研中的作用,并且分析了一些学派、团队形成的过程;刘萍等[12]构建了加权文献引文网络,并结合传统引文网络指标和学者文献的引用关系,对学者的学术影响力进行综合评测。
由于普通的点边网络无法表示网络中的高阶的信息关联,所以超网络模型逐渐被引入到网络分析任务中。例如,索琪等[13]就基于超图的超网络进行讨论,分析了这类超网络的结构及其演化机制;胡枫等[14]构建了基于超图的科研合作超网络模型,通过理论和实验数据分析了此超网络的超度,发现超度分布基本符合幂律分布;刘胜久等[15]从超网络的关联矩阵出发,对超网络进行分析研究,总结出了一些基于矩阵运算的构建超网络模型的性质;孙海生[16]选择前沿论文中的主题特征词作为研究对象并且构建超网络模型,通过对该超网络的特性分析表明,这种方法能够体现出特征词在各个聚类主题中的重要性;梁晓贺等[17]构建基于微博舆情的超网络模型,包含用户—观点—情感—时序四层,揭示了每层子网的特征信息,超网络模型的超边可用于舆情预警、舆情主题挖掘及舆情主题演化分析。
2 方法设计
2.1 方法流程
本文主要是分析引文网络中关键词的分布特性,并分析关键词-相关学者超网络模型特征。为了实现这两个研究目标,本文设计了一种方法验证流程,如图1所示。首先使用Python程序进行关键词爬取;然后把爬取到三个领域内的关键词输入到三个学术搜索引擎中进行搜索,并将得到的词的频数存入本地,同时将三个领域内的关键词在百度学术搜索引擎中进行搜索,把得到的近三年的词频和相关学者存入本地;最后,本文通过对爬取得到的关键词的数据进行拟合、分析,验证其频数是否符合Zipf定律并对构建的关键词-相关学者超网络模型进行分析。
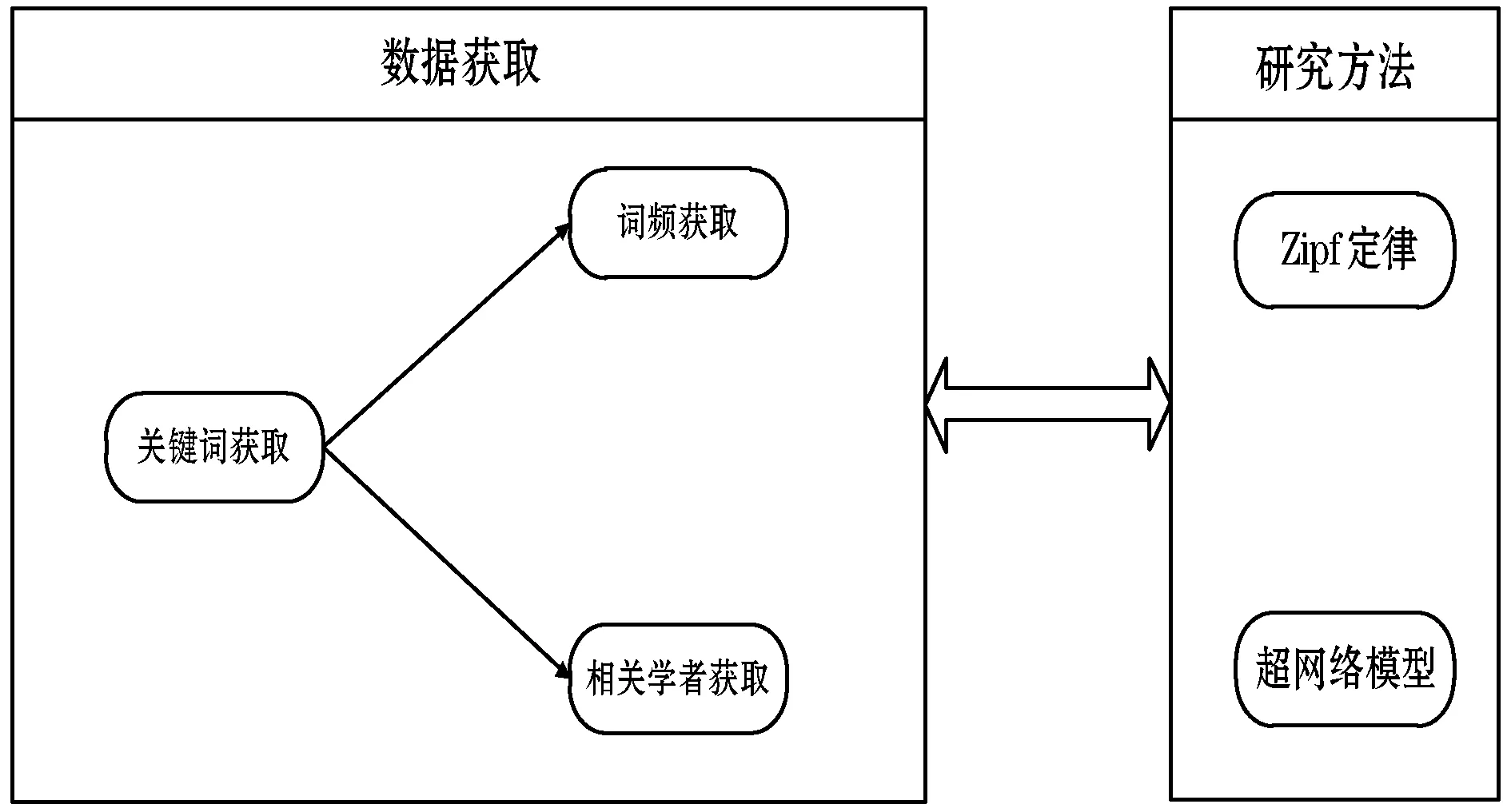
图1 本文主要研究方法流程
2.2 关键词爬取
本文研究的关键词是中文文献中的关键词,主要研究了人工智能、生物和财经三个领域内的关键词。
本文通过Python程序在中国科学等杂志期刊上爬取人工智能、生物和财经三个领域的文献,然后将关键词提取出来,对提取出来的关键词进行去除重复、去除单个字、去除英文处理,最终得到我们需要的关键词。主要步骤如图2所示。

图2 关键词获取流程图
(1) 论文获取。对本文研究的三个领域(人工智能、生物和财经)在中国科学等杂志期刊中进行搜索并爬取论文的作者、关键词、摘要等内容。
(2) 关键词提取。在爬取得到的论文中将关键词提取出来。
(3) 关键词筛选。将提取出来的关键词做去重、去单个字和去英文处理。
2.3 关键词词频与相关学者获取
本文研究的关键词词频是指关键词在搜索引擎中搜索了以后得到的搜索结果数。如图3所示,椭圆框里面的搜索结果为关键词词频。

(a) 知网关键词词频示例

(b) 百度学术关键词词频示例

(c) Bing学术关键词词频示例图3 三个搜索引擎中关键词词频示例
另外,本文还对三个领域内的关键词在百度学术搜索引擎中近三年的词频分布、与关键词相关的学者进行分析研究,图4为获取的百度学术中近三年词频和相关作者展示。长方框内为关键词2018年、2017年和2016年的词频,椭圆框内为与此关键词相关的学者作家。

图4 百度学术搜索引擎近三年词频与相关学者
2.4 Zipf定律
Zipf定律最早由美国语音学家George Kingsley Zipf提出,是最早被提出的文献计量学定律之一。Zipf定律的描述[20]如下: 设一个文本为T(词量充分多),其含有W个不同的词。若将这W个不同的词在文本T中出现的频次f统计出来,并且把词的频次按照从高到低的顺序排列起来,然后用自然数顺序从1(对应最高频次)到s(对应最低频次)将每个频次编上序号r(r=1,2,…,s),则rf=c(c为一常数)。还有另外一种指数形式p(r)=Cr-β,其中p(r)为排序在第r位置的词出现的频率,β为Zipf指数,C为常数。
Zipf定律的提出在文献计量学、语言学界引起轰动,通过其他专家学者陆续不断的研究,证实了各种语言的词频分布都基本符合这一定律,使得人们对词频的分布认识更为深刻,这一定律也对其他许多学科产生一定的影响[18-20]。构建Zipf实验的算法部分MATLAB伪代码如下:
data=xlsread(′Bing学术-财经.xlsx′);
x=data(:,2);
y=data(:,1);
loglog(x,y,′.′);
xlabel;
ylabel;
2.5 超网络模型
目前为止,对于超网络的概念并没有明确的定义,在学术界现在公认的超网络的定义主要有两种:基于超图的超网络和基于网络的超网络。基于网络的超网络是指那些链接方式比较复杂,规模比较巨大的网络,还有一些超网络是一个网络中嵌套着另一个网络的大型网络,这些都是基于网络的超网络(Supernetwork)[21-22]。

本文中构建的超网络模型是基于超图的超网络,其中关键词作为超网络的超边,相关知名学者作为超网络的节点。基于构建的关键词-相关学者超网络模型,可以构建出超网络在双对数坐标下的超度分布,具体算法如下:
(1) 初始化:超网络中的节点vi,i=1,2,3,…,n。
(2) 递归:检查超网络中的所有节点,若节点vi和vj属于同一关键词,那么就将节点vi和vj放入表示该关键词的超边E中。
(3) 算法结束:超网络中的所有节点全部检查完毕。
构建关联矩阵部分Java代码和构建超网络模型的超度分布的部分MATLAB代码如下:
构建关联矩阵
Scanner sc=new Scanner(System.in);
int VexNum=sc.nextInt();
int HyperEgeNum=sc.nextInt();
int CMatirx=new int[HyperEgeNum+1][VexNum+1];
int indexVex=new int[HyperEgeNum+1][VexNum+1];
int c=0;
try {
Scanner in=new Scanner(new File(".txt"));
while (in.hasNextLine()) {
int k=1;
c++;
for (int j=0;j k++; } } in.close(); } 超网络的超度分布 B=关联矩阵; A=B′; df=sum(A>0); pp2=tabulate(df); sw=find(pp2(:,3)>0); x_value=pp2(sw,1); y_value=pp2(sw,3)/100; p3=polyfit(log(x_value),log(y_value),1); kx=p3(1); b=p3(2); x2=minvalue:maxvalue; y2=exp(polyval(p3,log(x2))); loglog(pp2(sw,1),pp2(sw,3); xlabel;ylabel; 由于目前还没有比较完整、权威的中文文献关键词数据库,本文的所有实验数据集均由互联网搜集所得,此数据集是通过我们设计的一个Python爬虫程序爬取得到。 首先,本文在《中国科学》期刊分三个领域(人工智能、生物、财经)共爬取约6 000篇文章(每个领域约2 000篇)并将关键词提取出来,得到约18 000个关键词。又由于在这约18 000个关键词中存在单个字、纯英文、重复以及一些地名人名,对其进行去重和筛选,最终得到能用于本文研究的关键词共有约7 500词(每个领域约2 500词)。其次,我们将这7 500个关键词分别输入到百度学术、Bing学术和知网这三个学术搜索引擎中进行搜索并将其得到的搜索结果数进行统计,然后对所得结果数按照降序排列,即得到我们最终需要的研究数据。另外,在百度学术搜索引擎中,本文不仅爬取了总的结果数,还爬取了近三年(2018、2017和2016年)的搜索结果数和与此关键词有关的相关知名学者。 本文主要通过三方面对关键词的分布特性进行研究。一方面是验证不同学科的关键词词频与其排名分布是否符合Zipf定律,另一方面是分析不同学科内的关键词近几年内的分布是否符合Zipf定律。本文将词频与其排名放在双堆数坐标系中进行拟合,观察其分布是否符合幂律分布,若符合幂律分布,则关键词分布符合Zipf定律。最后,本文还对构建的关键词-相关学者超网络模型进行分析,超网络模型的分析主要是分析其超度的分布,本文在双对数坐标系下将关键词-超网络模型超度分布拟合出来,从而对此超网络模型进行进一步研究。 3.2.1Zipf定律验证 图5是人工智能、生物和财经三个领域的关键词在知网、百度学术和Bing学术三个学术搜索引擎中搜索结果数目和其对应排名在双对数坐标下的关键词词频排名分布图。 (a) 知网-人工智能 (b) 知网-生物 (c) 知网-财经 (d) 百度学术-人工智能 (e) 百度学术-生物 (f) 百度学术-财经 (g) Bing学术-人工智能 (h) Bing学术-生物 (i) Bing学术-财经图5 搜索结果数与排名分布图 可以看出,除了尾部以外,所有的点都几乎分布在同一条直线上。我们对上面三组数据进行拟合,得到如表1所示的回归方程。从表1中的回归方程中可以发现,关键词的搜索结果数和与其相对应的排名之间是近似幂律分布。中文文献关键词的分布在各自的领域内基本符合Zipf定律。 表1 搜索结果数与排名分布回归方程 图6是人工智能、生物和财经三个学科领域的关键词在百度学术这个学术搜索引擎中近三年(2018年、2017年和2016年)的搜索结果数目与其对应排名在双对数坐标下的关键词词频排名分布图。 (j) 人工智能-2018年 (k) 人工智能-2017年 (l) 人工智能-2016年 (m) 生物-2018年 (n) 生物-2017年 (o) 生物-2016年 (p) 财经-2018年 (q) 财经-2017年 (r) 财经-2016年图6 近三年搜索结果数与排名分布图 可以看出,除去尾部以外的部分,所有的点依然都几乎分布在同一条直线上。对上面三组数据进行拟合,得到如表2所示的回归方程。从表2中的回归方程中可以发现,关键词近三年的搜索结果数和与其相对应的排名之间依然是近似幂律分布的。中文文献中的关键词在各自的领域内,每年都基本符合Zipf定律。 表2 近三年搜索结果数与排名分布回归方程 基于以上实验结果,本文得出了如下结论: (1) 在每个搜索引擎中三个学科领域内的Zipf指数是相差不多的(比如在知网中人工智能、生物、财经的Zipf指数分别是-2.2、-2.299、-2.287); (2) 人工智能和财经领域在Bing学术搜索引擎中的R指数都是0.8左右,比在知网和百度学术搜索引擎中的R指数0.9小很多; (3) 在近三年的词频分布中,三个学科领域都有较好的拟合结果,R指数基本都在0.95左右。 在上述分布曲线图中,可以明显看出分布图的尾部呈现急速的下垂现象,导致这种现象的主要原因是在关键词词频比较低的区域的关键词数量急剧增加。为了分析这种现象,本文对三个学科领域低频词的研究。表3为三个学科领域一些低频词代表,研究发现低频词急剧增加的原因主要有两方面:一方面是这些低频词在自己学科领域内比较专业,都是一些专业名词,比如生物领域内的固氨率、共基质代谢等词都是专业名词;另一方面,还有一些低频词在自己的领域内不是研究热点,没有得到大家的关注,比如克隆网络和财经伦理等词,都是比较陌生的关键词。由于这些低频词的急剧增加导致尾部出现急速下垂现象,但是对大多数的文本来说,Zipf定律对词频的高中区域基本比较吻合。 表3 低频词词频统计 续表3 此外,由于每个学术搜索引擎都是每时每刻在更新变化,故在本文中对上述数据的分析可能略有一些波动,但是如果某个关键词没有在短时间内被极度关注或者成为一个研究爆点,上述实验结果具有一定的代表性。 本文又根据关键词的词频描绘出三个知识领域的词云图。图7为三个领域的关键词的云词展示。 (a) 人工智能 (b) 财经 (c) 生物图7 关键词词云可视化 由图7可以清楚地了解到在每个学科领域中目前较为关注的热点话题,比如在人工智能词云图中可以发现目前研究热点为机器人、专家系统、控制等。 3.2.2超网络模型的构建与分析 为了更详细地了解中文文献中关键词的分布,我们分研究领域构建了三个关键词-相关知名学者超网络模型,并对这些超网络模型做了如下分析。图8为中文文献中关键词在人工智能、生物和财经三个领域内构建的关键词-相关知名学者超网络模型的超度分布图。其中,我们把关键词当作超边,把相关知名学者当作节点。 (a) 人工智能 (b) 生物 (c) 财经图8 超网络模型超度分布 可以看出,节点的超度分布大致呈幂律分布,说明每个关键词对应的相关知名学者在每个领域内都呈幂律分布,显示了无标度特性。根据数据拟合出来的回归方程如表4所示。 表4 超网络模型超度分布回归方程 可以看出,关键词-相关知名学者超网络模型在人工智能、生物和财经三个领域中的幂指数分别为2.857 7、2.220 6、3.058 4。 在超网络动态模型动态演化时,累积性和优先连接性是无标度超度分布呈现幂律分布的最主要的两个原因。累计性就是节点的增加,对应本文中所构造的超网络模型就是指研究某个关键词的相关学者的增加;优先连接性是指度比较大的节点优先连接的概率较大,在本文中指相关学者在选取研究话题时通常会优先选取比较热门的话题来研究。 本文从Zipf定律和超网络等几个方面对中文文献中的关键词进行分析研究。通过对三个领域内的关键词在三个代表性的学术搜索引擎中的搜索结果数据的研究得到验证,在每个研究领域内,关键词搜索结果数和其排名符合Zipf定律。探讨了关键词近三年的搜索结果数与其排名是否符合Zipf定律,实验表明,在每个领域内关键词近三年的搜索结果数和其排名也是符合Zipf定律的。构造了一个关键词-相关知名学者超网络模型,通过对其超度分布的分析,在每个领域内关键词对应的相关知名学者遵循幂律分布,表现出比较明显的无标度特征。3 实 验
3.1 数据集说明
3.2 实验结果及其分析

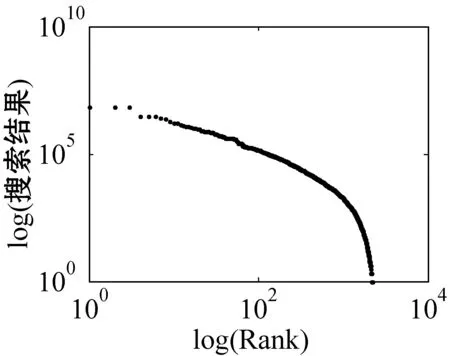
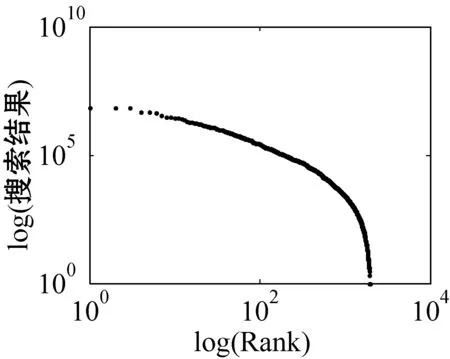







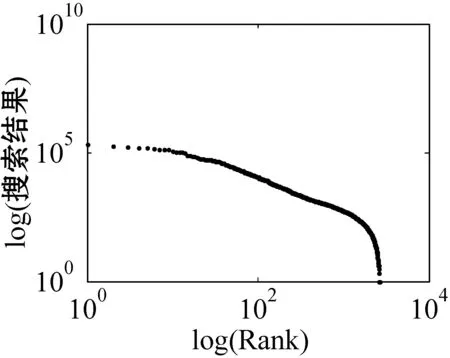
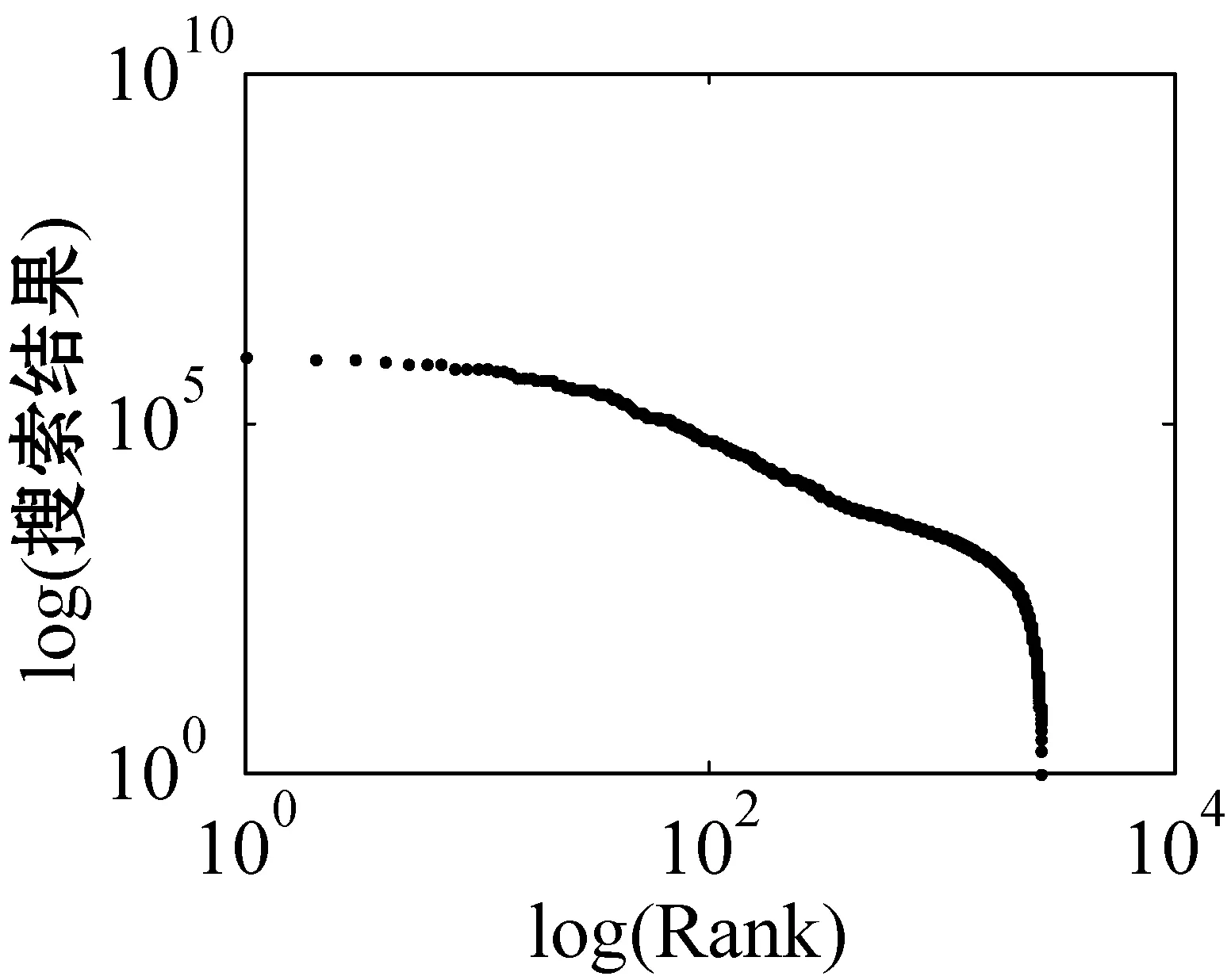
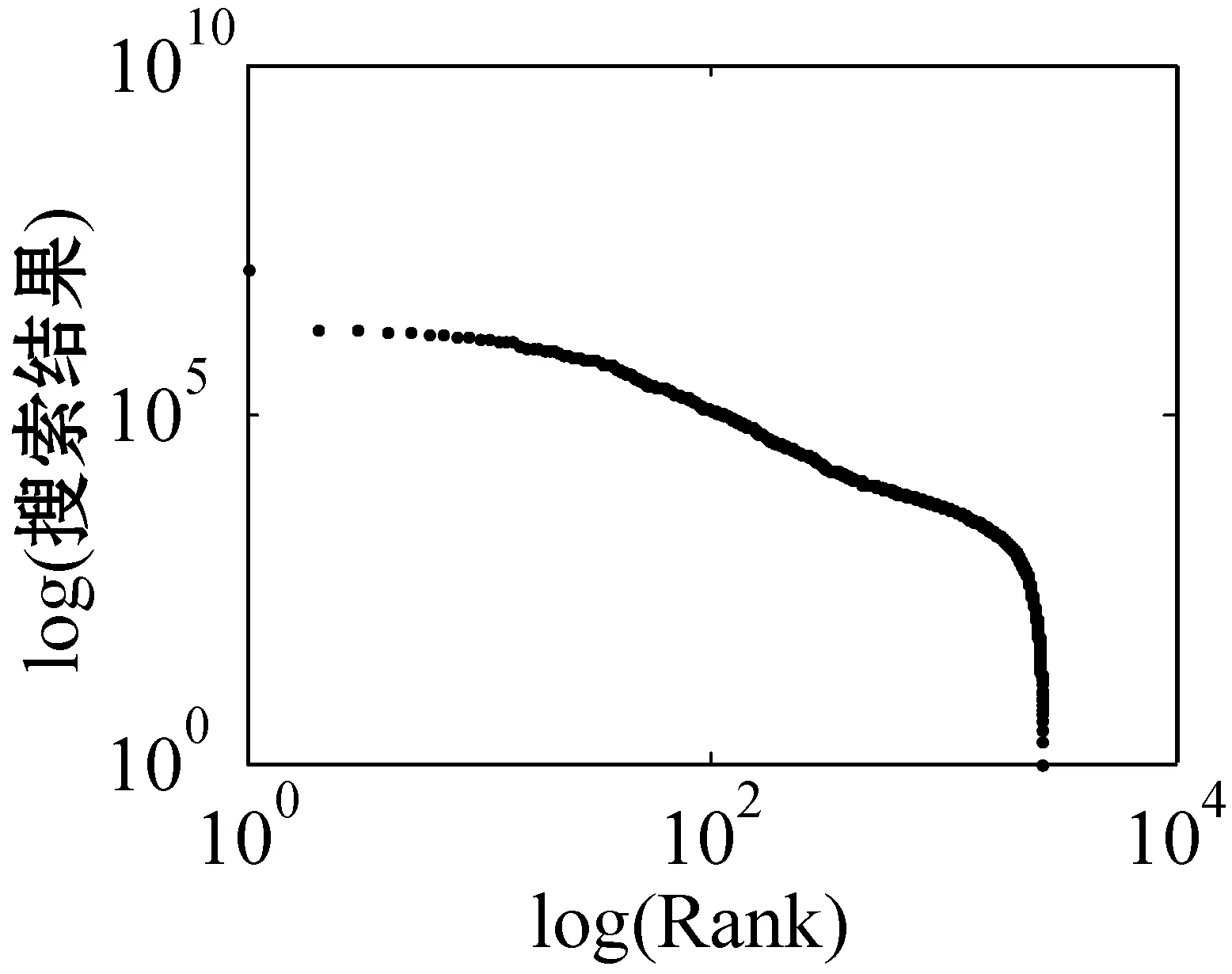

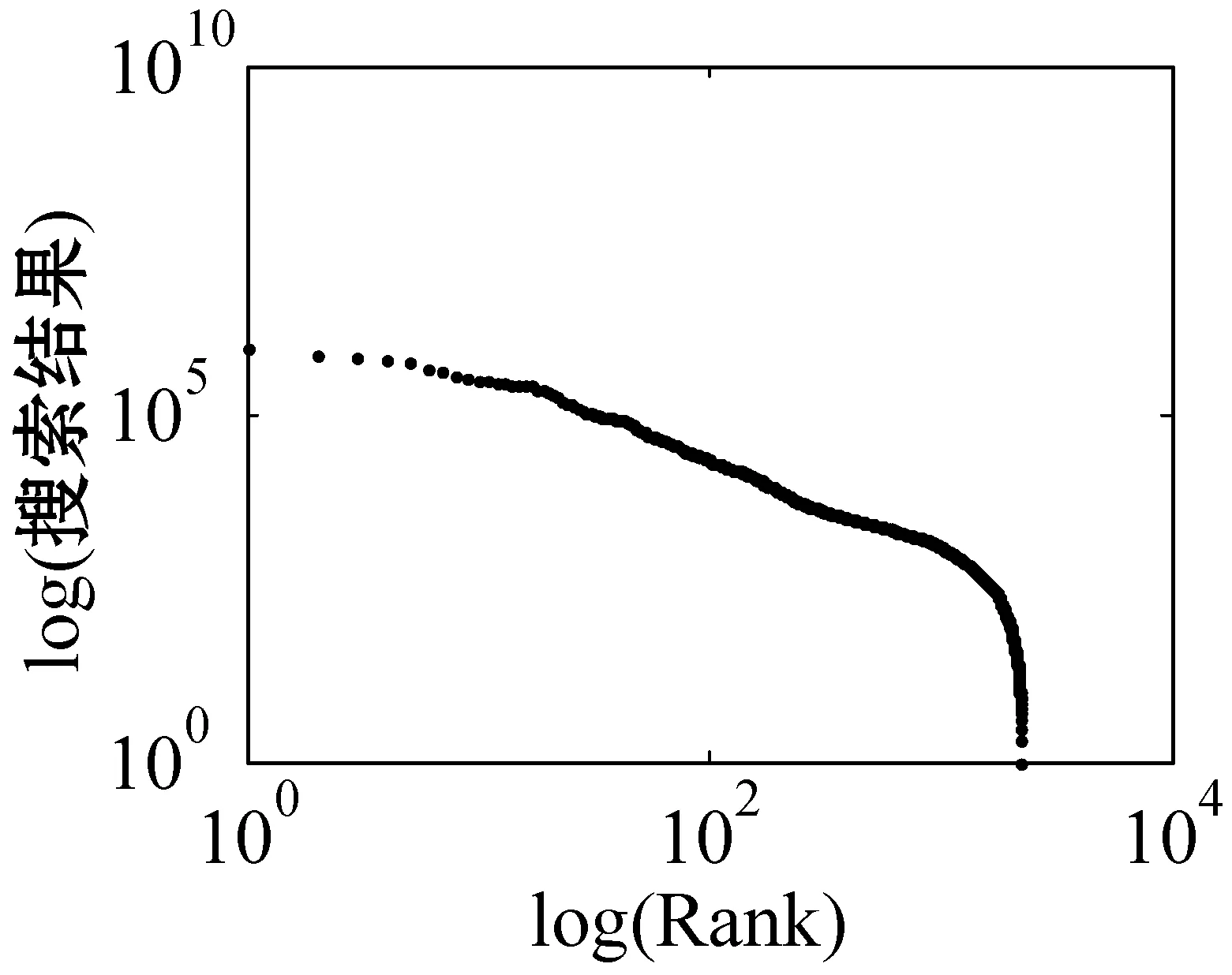
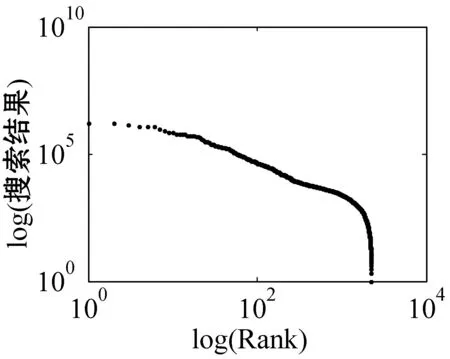


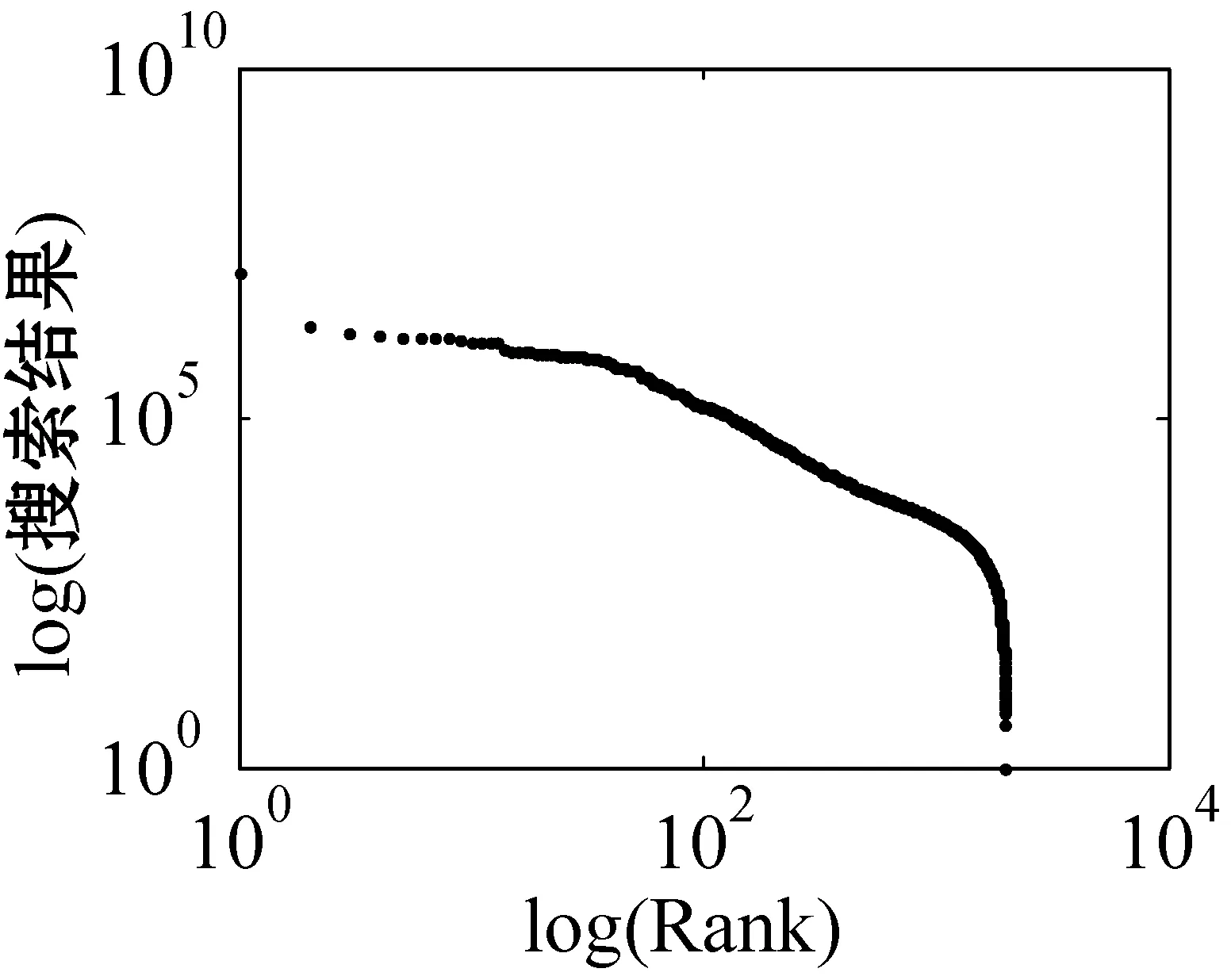






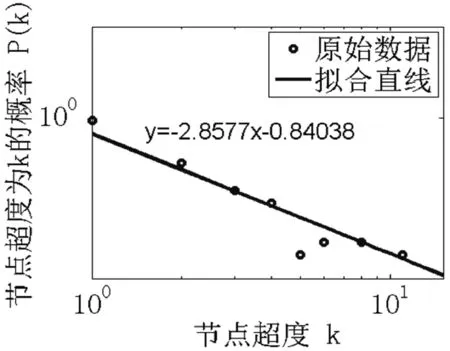



4 结 语
