一种基于引力搜索机制的云工作流调度算法

王旖旎 李 明

1(重庆商务职业学院 重庆 401331)2(重庆大学计算机学院 重庆 400044)

0 引 言

云环境中的工作流调度广泛应用于科学研究与商业领域，如天文学、天气预测、医疗和生物信息学等。工作流规模较大，包括大量独立和依赖型任务，需要规模较大的计算、通信和存储环境实现其调度与执行。工作流调度的实质是具有偏序关系的任务至云资源间的映射问题，通常以满足用户定义的相关QoS约束为目标完成工作流任务的执行[1]。传统的网格工作流调度问题更加注重调度效率，即优化调度时间，没有考虑资源使用带来的调度代价[2]。云计算环境中，资源的处理能力和处理租用价格不一，资源能力越高，价格也越高。此时，具体应用的调度策略所带来的调度时间和调度代价也不相同。因此，同步考虑工作流执行的时间和代价，这将更加符合云环境下工作流调度的场景。

然而，现实的情况是，优化工作流的调度时间和调度代价本身是两个相互冲突的目标。若要降低调度时间，则工作流任务将偏好在性能更高的资源上执行，而资源性能越高，其利用代价也将越高；反之，若要降低调度代价，则工作流任务将偏好在价格更低的资源上执行，而资源价格越低，其性能也将越低，此时调度时间也将延长。为了解决这一问题，提出一种基于引力搜索算法的工作流调度算法，利用引力搜索的进化机制，通过代理适应度的评估，得到最终在调度时间和调度代价上综合性能最优化的任务映射方案。

1 相关研究

为了解决工作流调度问题，启发式调度算法是常规方法。文献[3]提出LOSS和GAIN两种算法分别用来优化预算约束下的时间和代价，但仅涉及单目标优化。文献[4]讨论了IaaS云环境中的代价和截止时间约束工作流调度，但所考虑的资源仅为同质资源模型。文献[5]提出两种云工作流调度算法：一阶段算法IC-PCP和两阶段算法IC-PCPD2。两种算法可以在多项式时间内得到载止时间约束下的代价最小调度方案。文献[6]提出了在混合云中截止时间约束的代价最小化调度算法HEFT，利用子截止时间的概念进行资源的重调度，并实现了代价最小化。文献[7]则实现了包任务在截止时间约束下的代价最小化调度，但仅适用于独立任务调度。文献[8]利用粒子群搜索方法求解了用户截止时间约束下费用最小化的工作流调度方案。文献[9-11]提出了一种截止时间与预算约束时工作流调度遗传算法，但也仅是实现执行代价或执行时间的单一优化。可以看出，以上启发式或元启式算法多数仅进行了垄断和单一目标优化。针对以上问题，本文将从优化调度长度和调度代价两个方面入手，提出新的云工作流任务调度算法，提升在两个指标上的综合性能。

2 问题模型

2.1 工作流模型

工作流应用可表示为有向无循环图DAG，G=(T,E)，如图1所示，其中：T={t1,t2,…,tn}表示任务集合；E表示有向边集合；一条边ti→tj表明前驱ti与后继tj间的执行次序约束。因此，任务tj在ti完成前无法开始执行。每个任务ti拥有以MI表示的计算负载属性。而每条边ti→tj拥有的属性为任务ti生成的输出数据量，该数据即执行tj需要的数据。若任务不存前驱，则可视为入口任务tentry；若任务不存在后继，则可视为出口任务texit。若工作流拥有多个入口任务，可添加零计算负载无数据输出的傀儡任务至工作流结构中。拥有多个出口任务的工作流也可作类似操作，不影响计算工作流调度时间和代价。

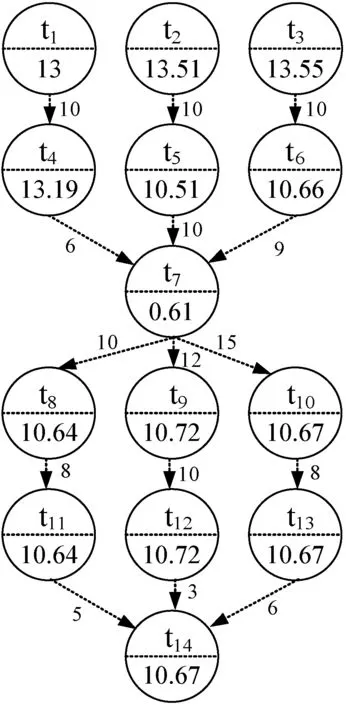
注：节点代表任务，有向边代表顺序关系，节点t1中任务标识下的数字13代表任务的计算负载量，有向边上的数字代表有向边对应的出发任务节点产生的数据量

图1 工作流示例

2.2 云服务模型

假设云服务包含m个虚拟机，表示为V={v1,v2,…,vm}。每个虚拟机拥有自身的计算能力，以MIPS衡量。所有虚拟机之间是全连通结构，可寄宿于一个或多个物理云服务器上。传输任务ti至tj的输出数据的时间可考虑为通信开销时间。若任务ti与tj执行于同一虚拟机上，则通信开销为零。

3 问题定义

3.1 相关参数定义

文中相关参数含义说明如下：

N：种群大小；

n：工作流中任务数量；

ti：任务i；

m：可用虚拟机量；

vj：虚拟机j；

Xi：代理i；

Xbest：至目前为止的最优代理；

α：计算适应度时调度长度和调度代价的权重；

fiti：代理i的适应度；

Mi：代理i的质量；

σ：价格模型中的随机变量；

Vcbase：最慢虚拟机的基准价格；

digvj：虚拟机vj的性能下降；

γ：控制引力常量偏差的常量；

δ：质量门限值。

相关约束和假设如下：

1) 考虑虚拟机的性能变化来计算执行任务时的有效CPU周期，对于虚拟机vj，性能变化表示为degvj，利用degvj，任务ti在虚拟机vj上的执行时间可重写为：

(1)

式中：Load(ti)表示任务ti的计算负载；Capacity(vj)表示虚拟机vj的计算能力。

2) 计算执行代价时考虑单位支付时间τ。若租用虚拟机的时间小于τ，则按照全部时间单位τ支付费用。

3) 利用虚拟机时需要考虑虚拟机的初始启动时间，即在计算调度长度时需要加入虚拟机启动时间，同时将虚拟机的关机时间也考虑至调度长度中。

4) 虚拟机之间以相同带宽进行全连通。

3.2 优化问题描述

1) 调度长度Makesapn计算。调度长度即为整个工作流的总体执行时间，包括租用虚拟机的启动时间、执行时间、虚拟机间的数据传输时间和虚拟机的关机时间。假设数据正在传输过程中虚拟机无法执行任务，则调度长度等于虚拟机启动时间、所有虚拟机中虚拟机时间VM-time的最大值及虚拟机关机时间之和。VM-time[i]表示最后一个时间戳至虚拟机vi执行其指定任务的时间间隔。启动时间和关机时间仅需计算一次的原因在于虚拟机仅需在首次启动并在最后一次关机。因此，调度长度为：

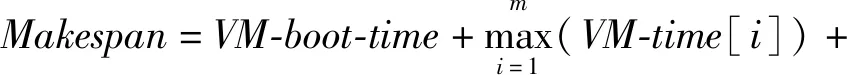
VM-shutdown-time

(2)

2) 调度代价cost计算。调度模型中，云服务器由拥有针对不同负载类型的不同计算能力的虚拟机组成，式(1)表示任务ti在虚拟机vj上的执行时间，令τ表示任务的单位支付时间，Vcbase表示最慢虚拟机的基准价格，cost(ti,vj)定义为任务ti在虚拟机vj上的执行代价：

(3)

式中：σ表示随机变量，以产生不同的虚拟机价格组合和能力,CCvj表示虚拟机vj的CPU周期数，CCslowest表示虚拟机中最慢CPU周期数。令Bi,j表示布尔变量，定义为：

(4)

因此，工作流的调度代价为：

(5)

3) 最优化问题。云工作流的调度目标即是最小化调度长度和调度代价，可表示为最小化两个目标的线性组合，将其形式化为：

Minz=α×Makespan+(1-α)×Costtotal

(6)

(2) 0≤α≤1

其中：约束条件(1)表明工作流中的任一任务仅能分配至一个虚拟机上；约束条件(2)表明权重因子，表示算法对于调度长度和调度代价优化的偏好。

4 算法设计

本文设计的算法称为混合引力搜索算法，简称HGSA。

4.1 初始种群生成方式

以HEFT算法[13]的输出结果作为初始种群的生成方式，即以最小化最早完成时间为目标进行任务调度，具体包括两个步骤：

步骤1计算任务优先级。该阶段中，每个任务的优先级利用平均执行时间和平均通信时间计算。优先级定义为升秩值表达。根据由高到低的优先级排序得到任务调度次序，从而满足给定工作流的任务执行顺序约束。任务ti的优先级定义为：

(7)

式中：wi,avg表示任务ti的平均执行时间；ci,j,avg表示任务ti与tj间的平均通信时间。

步骤2任务与虚拟机间的映射。通过在所有可用虚拟机上计算任务最早开始时间EST和最早完成时间EFT，根据任务的优先级，得到任务的调度结果。

4.2 代理表示

算法中，工作流中任务与虚拟机间的映射可视为一个代理agent。对于拥有n个任务的工作流和m个虚拟机的云服务器的调度环境，代理i可表示为维度为1×n的矢量，即：

(8)

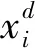
表1 代理示例

4.3 适应度评估

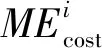
(9)

4.4 调度方法

HGSA算法包括两个阶段。第一阶段仅集中于调度长度的优化，第二阶段优化调度代价，同时最小化适应度值，适应度则同步考虑了调度长度和调度代价。第一阶段产生的结果可指导引力搜索算法GSA中粒子的运动，可以改进传统GSA的随机初始化粒子运行机制。算法具体步骤为：

步骤1以HEFT算法的输出结果作为种子得到初始种群，以更少的迭代次数产生更优的解。

步骤2根据适应度函数保留当前代中的最优粒子，确保最优代理在未来代中不被剔除。

步骤3质量小于门限值δ的代理从当前种群中剔除，由于该类代理在种群更新中贡献较少。剔除以上代理后，添加以最优代理为基础的新的代理至种群中，改进种群全局适应度。

4.5 粒子位置更新

考虑系统包含N个代理，代理i的位置定义为：

(10)

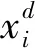
(11)

式中：ε表示极小常量；Ri,j(k)表示第k次迭代时代理i与代理j间的欧氏距离，定义为：

(12)

若代理i在维度d上的总引力为其他代理在维度d上产生的引力的随机权重和，则：

(13)

式中：randj表示[0,1]间的随机数。可知，代理i在第k次迭代时在维度d上的加速度为：

(14)

由此可知，代理的位置和速率更新可计算为：

(15)

(16)

G(k)为引力常量G0和迭代次数k的函数，定义为：

(17)

式中：γ表示较小常量，用于控制引力常量的降低；G0在算法开始时初始化，并随着算法的执行而降低，以改进搜索准确性。

4.6 算法具体步骤

算法1是HGSA的具体执行过程。步骤1为将任务在虚拟机间进行随机映射以产生初始种群，步骤2为将HEFT算法输出的结果播种至种群中。初始种群准备就绪后，种群中的代理需要迭代若干次数以产生最终结果，即步骤3-步骤16。迭代的第一步是计算引力常量，即步骤4。然后在步骤5中，根据式(9)计算每个代理的适应度。根据适应度值，步骤6为识别种群中的最优代理和最差代理，步骤7为计算所有代理的质量。步骤8为通过计算纯引力、纯加速度和速率，以更新每个代理的位置。剩余步骤中，算法用新的代理取代劣势代理。新代理的生成方式为将任务映射至随机选取的虚拟机上，剩余映射方案则仍然维持不变。

算法1HGSA算法过程

输入：工作流应用W，云服务资源CSS

输出：任务映射结果M

1. 初始化拥有N个随机代理的种群X

2. 利用HEFT生成的解代替种群中的一个代理

3. fork=1 toMAX_ITERATIONdo

4. 利用式(19)计算G(k)

5. 利用式(10)计算适应度值fiti

6. 基于计算的适应度值识别最优和最差代理

7. 利用式(11)计算代理质量Mi

8. 利用式(13)-式(18)计算每个代理的速率与位置

9. fori=1 toNdo

10. ifMi<δthen

11. 赋值Pos为区间[1,n]间的随机整数值

13. 赋值xposi为区间[1,m]间的随机整数值

14. end if

15. end for

16. end for

17. 基于适应度fiti寻找M个对应的最优代理

18. returnM

HGSA算法根据原始引力搜索算法的空间搜索步骤进行最优解搜索，因此其时间复杂度与GSA算法相同，同为O(N)，N为初始化的粒子数量。

5 算例分析

考虑一个Montage工作流进行算法算例分析，工作流包括16个任务，T={t1,t2,…,t16}，云环境包括4个虚拟机，V={v1,v2,v3,v4}，工作流的结构和虚拟机结构如图2和图3所示。4个虚拟机为全连通结构，算法分析的目标是以优化调度长度和调度代价为目标，将任务调度至虚拟机上执行。表2给出算例中的相关参数，表3给出算法步骤1描述的生成初始种群结构。

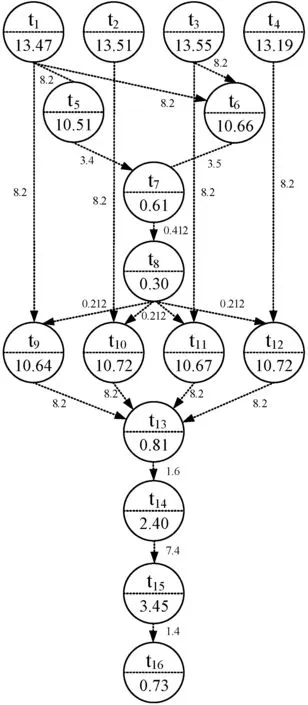
图2 算例应用的工作流结构

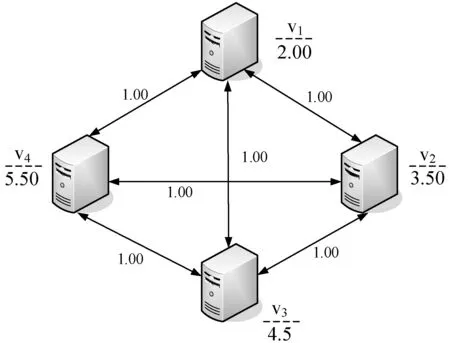
图3 云资源环境

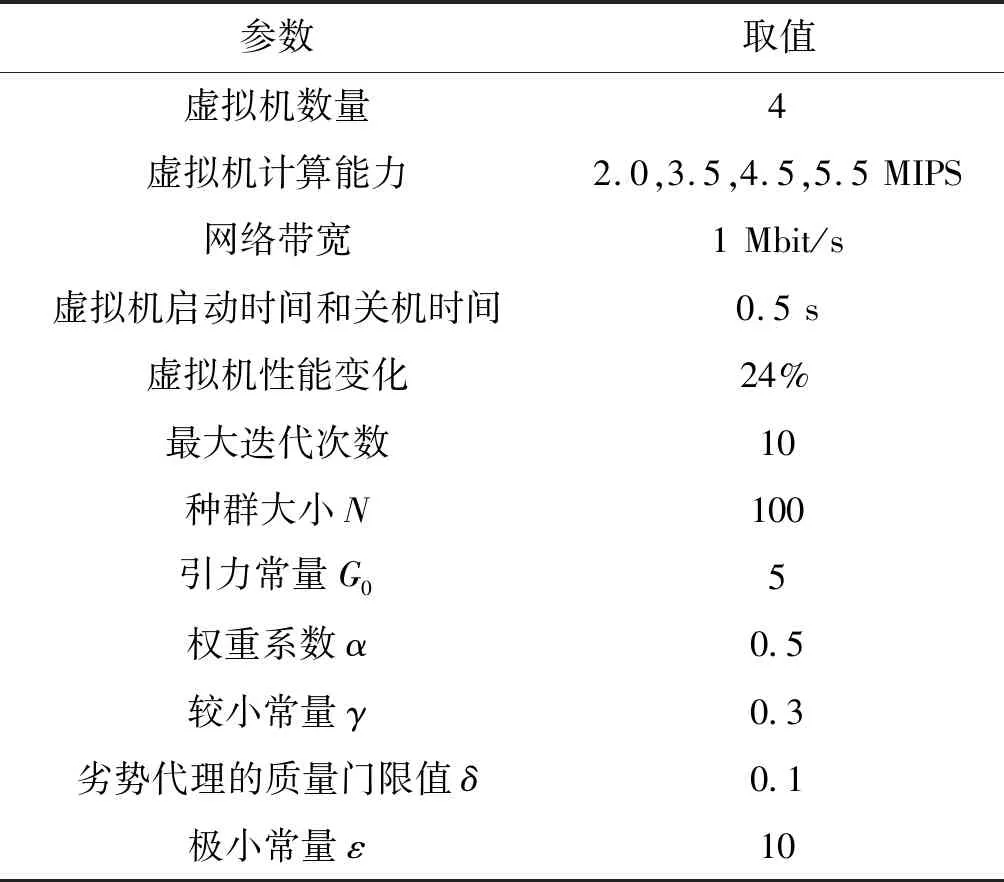
参数取值虚拟机数量4虚拟机计算能力2.0,3.5,4.5,5.5MIPS网络带宽1Mbit/s虚拟机启动时间和关机时间0.5s虚拟机性能变化24%最大迭代次数10种群大小N100引力常量G05权重系数α0.5较小常量γ0.3劣势代理的质量门限值δ0.1极小常量ε10

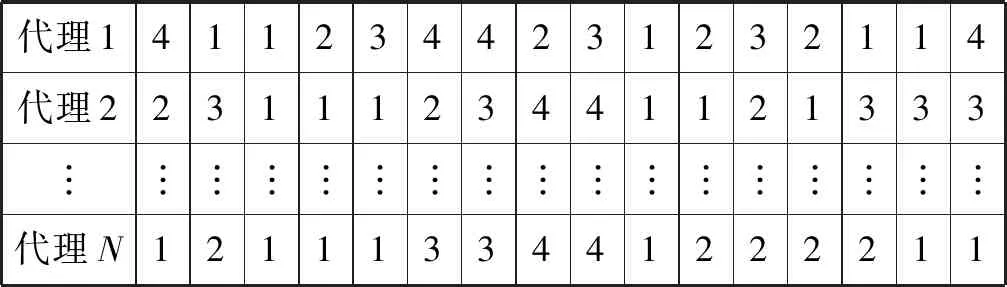
表3 代理初始种群

利用式(8)计算任务优先级，根据优先级的降序排列，任务被依次映射至一个虚拟机上，使得任务的最早完成时间达到最小化。表4为算法得到的任务优先级与相应任务映射情况。同时可以计算出HEFT算法得到的调度长度和调度代价分别为36.57 s和＄50.31。

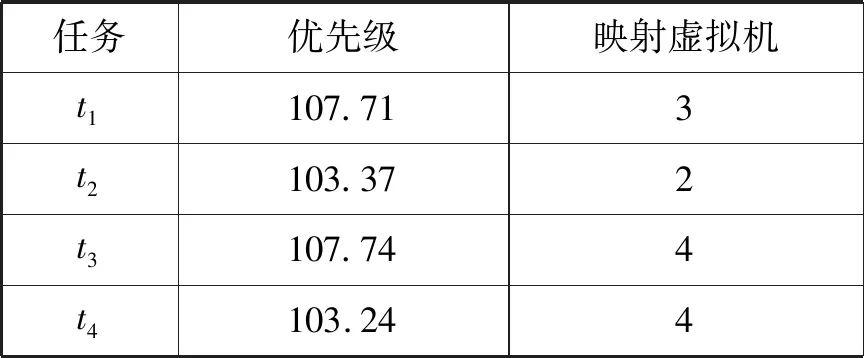
表4 任务优先级及映射

续表4

图4显示了HEFT生成的映射方案加至初始种群以取代劣势代理的示例，即算法步骤2。

图4 HEFT解加至种群

至此，当前种群包含HEFT生成的代理和随机生成的代理，种群按照算法中步骤3-步骤16的迭代步骤进行进化。表5给出了每次迭代中最优代理的相关值情况，表6则是相应的调度结果，此时的调度长度为32.64 s，调度代价为＄47.71。

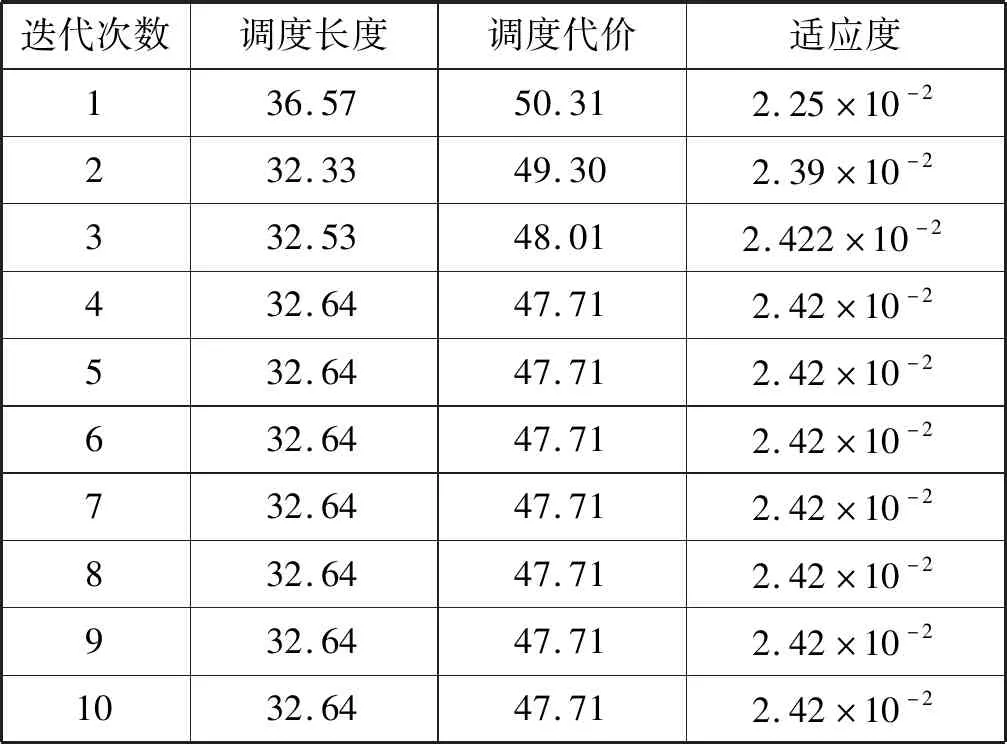
表5 最优代理结果

表6 调度结果

6 仿真实验

6.1 实验配置与性能指标

本节利用CloudSim平台下的仿真实验的方法对工作流调度算法进行性能分析，测试算法包括标准GSA算法[14]、HEFT算法[13]和HGA算法[15]。除种群模式设置为500，最大迭代次数设置为200之外，其他参数与表2相同。

通过标准化方法对调度长度和调度代价作出处理，以调度长度比率SLR和调度代价比率MCR作为性能评估指标，分别定义为：

选取四种不同科学领域的工作流结构作为数据测试源，包括：Epigenomic工作流(同时拥有计算密集型和网络密集型任务)、Montage工作流(网络密集型任务)、CyberShake工作流(同时拥有I/O密集型和网络密集型任务)以及Inspiral工作流(计算密集型任务)。工作流的具体结构可参见文献[12]。

6.2 实验结果

图5为四种工作流在不同任务规模下得到的SLR和MCR指标情况。可以看到，在所有工作流类型中，HGSA算法的MCR指标是优于HEFT、HGA和GSA算法的，这说明初始种群的优化配置和引力搜索机制可以得到代价更低的工作流调度解。比较标准的引力搜索GSA算法，该算法未优化初始种群；而比较混合遗传算法HGA，该算法则在种群位置更新上不如本文算法效率高。HEFT算法在进行工作流调度时，仅考虑了任务的执行时间优化，因此其代价性能是最差的。此外，在SLR指标上，HEFT是所有算法中性能最好的，因为该算法是以调度长度为单目标进行的工作流算法。HGSA在SLR指标上优于HGA和GSA算法，虽然同为双目标优化算法，但本文在引力搜索机制上的改进，以及初始种群融入HEFT调度方案的优化方法，使得本文算法在搜索最优解时效率更高，在调度代价最优的同时仅仅牺牲了极小的调度长度性能，其综合性能是四种算法中最优的。而在四种不同类型工作流结构中得到的结果并没有体现很大差异，这说明本文算法在适应性上也是较优的。

(a) Epigenomic工作流

(b) Montage工作流

(c) CyberShake工作流

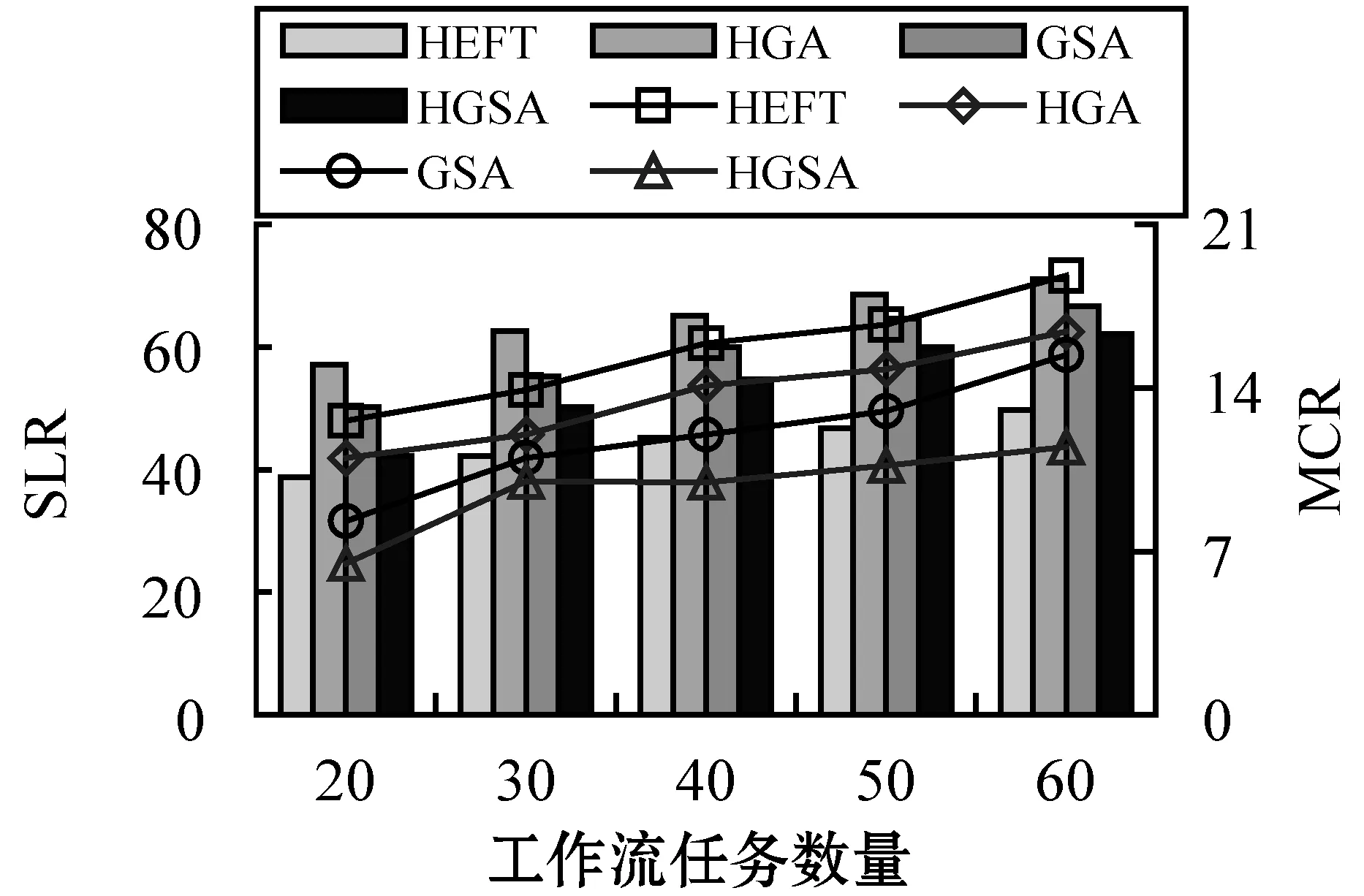
(d) Inspiral工作流图5 算法执行结果

7 结 语

为了同步优化云环境中工作流调度的长度和代价，提出了一种基于引力搜索算法的工作流任务调度算法。首先以异构最早完成时间机制生成引力搜索的部分初始代理，并结合随机生成方式，得到初始种群。然后，利用引力搜索的进化机制，通过代理适应度的评估，得到最终在调度时间和调度代价上综合性能最优的任务映射方案。利用一个算例对算法的有效性进行了论证与评估，结果表明，本文算法不仅可以得到最小的调度时间，调度代价也是对比算法中最小的。