深度稀疏自编码网络融合多LBP特征用于单样本人脸识别
2019-12-11赵淑欢万品哲郭昌隆
赵淑欢 万品哲 郭昌隆

摘 要:单样本人脸识别的关键在于充分挖掘单样本判别性信息,采用深度稀疏自编码网络与空频域多LBP特征融合进行特征提取。首先利用部分样本训练深度稀疏自编码网络,利用训练好的网络分别提取训练及测试集的特征;其次,利用二维离散小波变换将时域样本变换到频域,實现样本扩展,增加单样本信息并分别提取各域上的多LBP特征;最后利用协同表示对深度自编码网络及多LBP特征进行分类识别,融合识别结果获取最终分类结果。在AR及PIE数据库上的实验结果表明,该融合算法能提高样本判别性信息的提取,提高单样本人脸识别性能。
关键词:稀疏自编码;单样本人脸识别;空-频特征;多特征融合;二维离散小波变换;数据库
中图分类号:TP181文献标识码:A文章编号:2095-1302(2019)11-00-05
0 引 言
人脸识别是计算机视觉和模式识别领域重要的研究课题,在生活中应用广泛,如视频监控[1]、门禁[2]、行人再识别[3]、视觉追踪[4]等。尽管目前已有的人脸识别算法在特定环境下性能较好,但在实际测试中人脸可能含有多重面部变化,例如光照、阴影、姿势、表情、遮挡、不对齐等[5],因此人脸识别仍是一项具有挑战性的任务。
在许多实际应用场合中,每人仅有一个训练样本,例如ID卡认证、航空港监测等,导致在单样本识别中很难根据训练样本预测测试样本中可能出现的类内变化信息,因此单样本人脸识别仍是人脸识别中的难点。而传统的判别性子空间学习算法,例如线性判别分析(Linear Discriminant Analysis,LDA)[6]、基于Fisher的算法[7-8]在此种情况下会失效。基于表示的分类算法如稀疏表示(Sparse Representation-based Classifier,SRC)[9]和协同表示(Collaborative Representation-based Classifier,CRC)[10]要求每类用多个训练样本来有效表示测试样本,因此其在单样本识别中性能也会大幅下降。
为处理单样本人脸识别,研究人员提出多种算法,这些算法大致可以分为两类[11],即全局算法和局部算法。全局算法[12-13]用整张人脸图像作为输入,其主要思想是扩大训练样本数以捕捉类内信息。文献[14]中有两个方向,分别为虚拟样本生成和通用学习。虚拟样本生成利用真实训练样本合成虚拟样本,例如SPCA[15]和SVD-LDA[16]基于奇异值分解(Singular Value Decomposition,SVD)生成虚拟样本。这些算法的主要缺点是虚拟样本往往与训练样本高度相关,因此很难作为独立的样本进行特征提取[14]。
与基于虚拟样本算法不同,泛型学习方法通常会引入一个辅助泛型集,由不感兴趣的人员来补充原始的SSPP(Single Sample per Person,SSPP)图库集。Wang等人[17]假设不同的人之间共享相似的类内变化,据此利用泛型集估计类内散度。基于表示的算法包括扩展的SRC(ESRC)[12]、叠加SRC(SSRC)[18]、稀疏变化字典学习(SVDL)[13]、协同概率标签(CPL)[19]等。尽管这些算法可以在一定程度上提高单样本人脸识别算法的性能,但其性能仍严重依赖于巧妙的选取泛型集,理想的泛型集通常包括两个特点:需与训练样本有相似的拍摄场景;需包含足够的面部变化来预测测试样本中未知的变化。然而实际中很难收集到足够多的满足上述条件的泛型集。
局部算法利用局部面部特征识别测试样本。通常生成局部特征的方法是将一张人脸样本分割成一些重叠或不重叠的图像块,因此该类型的局部算法通常被称作基于块的方法[20]。该类方法中每个被划分的块都被看作是这个人的独立样本,基于该假设,研究人员将传统的子空间学习和基于表示的分类算法(例如PCA,LDA,SRC,CRC)进行扩展得到对应基于块的算法,例如块PCA[21],块LDA[22],块SRC(PSRC)[9]和块CRC(PCRC)[20],整合每个块的识别结果,得到最终的单样本人脸识别结果。Lu等人[14]提出一种判别性多流行学习算法(DMMA),将人脸识别转换成域到域的匹配问题。基于这一工作,Yan等人[23]通过整合多个局部特征提出多特征多流形学习方法来提升人脸识别性能。Zhang等人[21]通过加入另一个基于稀疏图的Fisher准则修正了DMMA算法,并为被划分出来的块学习一个判别性子空间。
最近,有研究人员尝试将泛型学习整合到基于块的方法中用于单样本人脸识别。例如,Zhu等人[24]从泛型集中提取块变化字典,然后将其与训练块字典串联来度量每个测试块的表示残差。这类算法与现有的基于块的表示方法相比可在单样本人脸识别中获得更好的性能,但理想的泛型集的获取仍是实际应用中的难题。
本文将样本投影到频域空间以实现样本的扩充,同时采用通用训练集采集部分类内变化信息,减小类内变化导致的单样本识别率下降现象,最后将空频域的识别结果进行融合获得最终的识别结果并在数据集上验证。
1 相关工作
1.1 深度稀疏自编码网络
SSAE是一种无监督特征学习算法,该算法采用层级训练方案构造深度网络,每一层包含两个部分,即编码器和解码器。编码器为一个函数,可将输入向量x映射到隐藏层表示a,即。解码器将隐藏层表示映射成一个重构向量y,即。其中W(1)和W(2)分别表示输入到隐藏层及隐藏层到输入的权重;b(1)和b(2)分别表示隐藏层单元和输出层单元的基;f(·)表示隐藏层单元的激活值,一般选用sigmoid函数;g(·)表示输出单元的激活值,一般设置为g(x)=x。对SSAE每层训练即最小化该层损失函数J:
式中:x(i)表示第i个训练样本,同时也是期望输出;y(i)表示对应预测输出;m表示训练样本的个数;h表示隐藏层单元的个数。相对熵惩罚项是为了增强隐藏层的稀疏度,参数表示第j个隐藏单元在训练集上的平均激活度,而ρ表示稀疏度参数,其值接近0,采用反向传播算法进行训练。
建立并训练SSAE后,隐藏层单元的激活度可作为下一层的输入。逐层训练SSAE的每一层,一旦SSAE的每一层都训练好,则编码器参数W和b可用于构建网络。
1.2 Huffman-LBP
为实现关于灰度任何单调变换的不变性,LBP仅考虑对比度值的符号[26],而LBP的这种属性有时会导致意想不到的混乱,致使两组不同的图像纹理进行LBP编码后得到相同的结果。霍夫曼编码通常用于无损数据压缩[27],然而很少有研究人员将霍夫曼编码应用于特征提取。为了解决LBP纹理信息丢失的问题,文献[25]首先采用霍夫曼编码对对比度值进行加权,以补充丰富的纹理信息,这种新方法被称为Huffman-LBP。
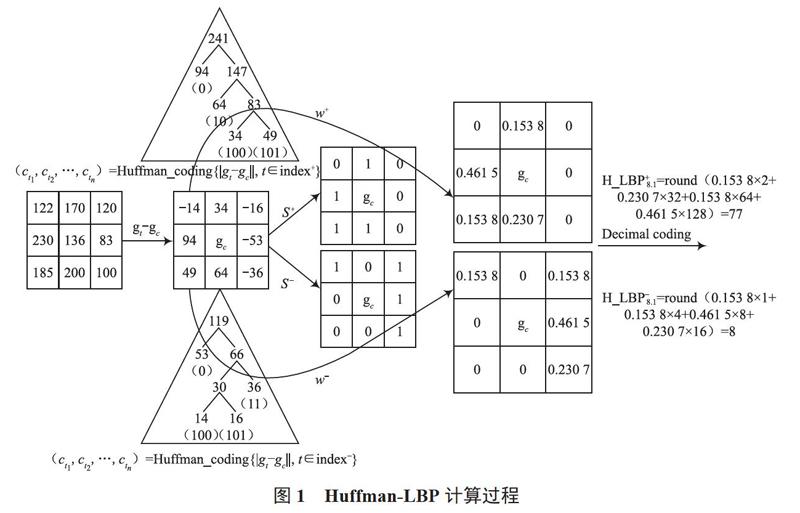
霍夫曼编码使用可变长度码字实现对源码元的编码,根据频率确定编码。频率较大的符号将用较少的位表示,即在霍夫曼树中,接近根节点的叶节点频率较小;远离根节点的叶节点频率较大。此外,每个叶节点霍夫曼码的长度与叶节点和根节点之间的距离一致。霍夫曼树,以gt-gc(t=0, 1, ..., p-1)的绝对值作为每个叶节点的频率,得到相应的霍夫曼码,根据代码长度,度量对比度值的权重。
图1所示为Huffman-LBP计算过程,从Huffman-LBP编码过程中可知Huffman-LBP包含正值和负值,它们表示对比度值的符号信息。且霍夫曼编码可以测量周围像素之间相对精确的重量关系。使用新颖的编码规则后,对比度值的符号不再是唯一的编码对象,对比度值的大小也将在编码过程中发挥作用。从图1可以看出,通过补充对比度值的权重信息可以提高LBP的辨别能力。虽然两组不同的图像纹理具有相同的二进制编码(s+和s-),但使用Huffman-LBP编码后它们会得到不同的特征值。
此外,一些LBP的改进算法可通过在编码过程中补充对比度值的评估来实现更好的性能识别,但必须考虑参数优化设置问题,例如选择LTP阈值和设置LMLCP层数将严重影响最终的识别结果,而霍夫曼编码将自动评估对比度值的权重,其优势在于其非交互性属性,这意味着它可以灵活工作。Huffman-LBP直方图可以通过累加像素的Huffman-LBP值来获得,然后将其用作模式特征来分类人脸图像。
1.3 本文算法
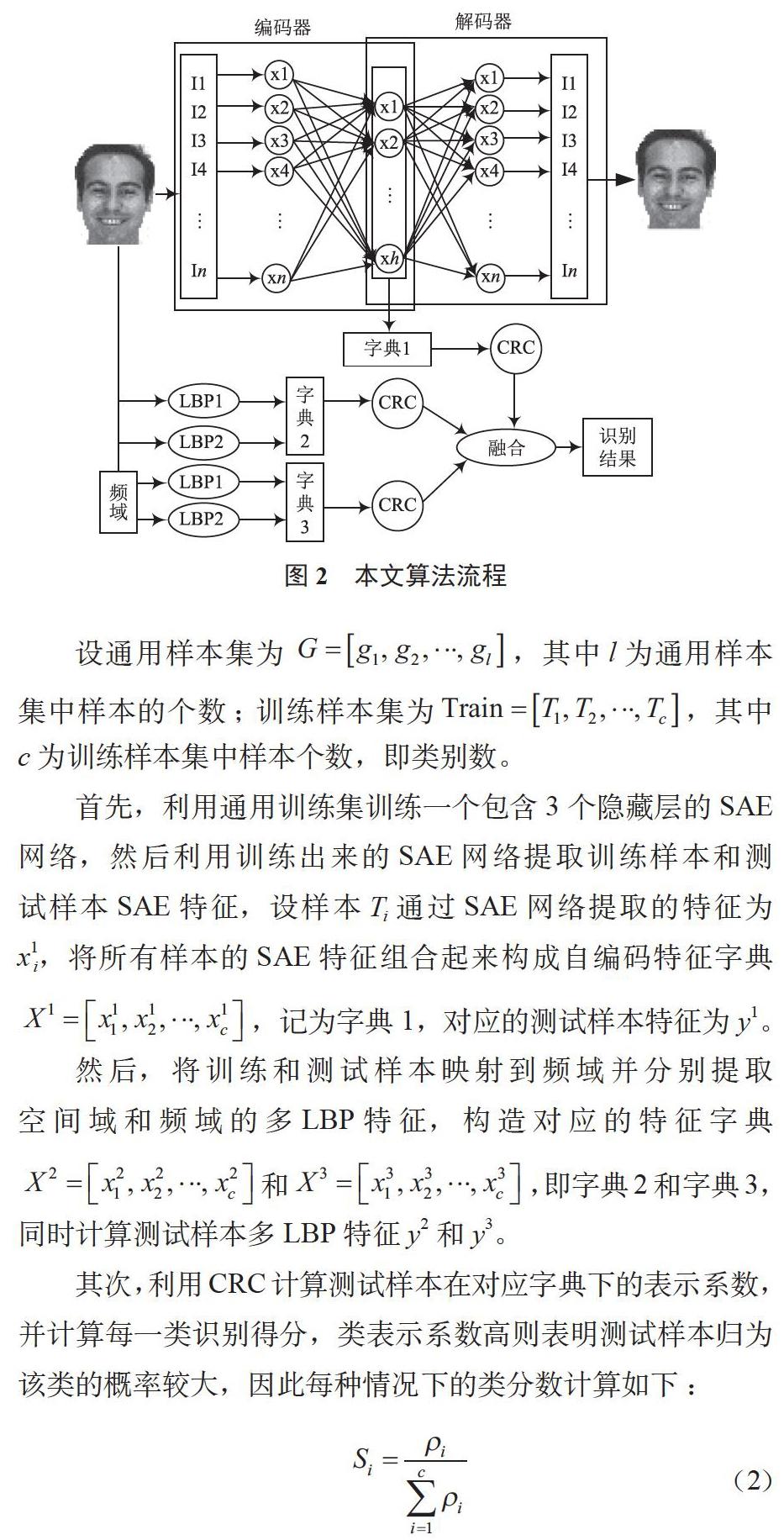
本文提出一种融合深度SAE及空频域的多LBP特征算法(SAE_MLBP)以解决单样本人脸识别问题,算法流程如图2所示。
设通用样本集为,其中l為通用样本集中样本的个数;训练样本集为,其中c为训练样本集中样本个数,即类别数。
首先,利用通用训练集训练一个包含3个隐藏层的SAE网络,然后利用训练出来的SAE网络提取训练样本和测试样本SAE特征,设样本Ti通过SAE网络提取的特征为x1i,将所有样本的SAE特征组合起来构成自编码特征字典,记为字典1,对应的测试样本特征为y1。
然后,将训练和测试样本映射到频域并分别提取空间域和频域的多LBP特征,构造对应的特征字典和,即字典2和字典3,同时计算测试样本多LBP特征y2和y3。
其次,利用CRC计算测试样本在对应字典下的表示系数,并计算每一类识别得分,类表示系数高则表明测试样本归为该类的概率较大,因此每种情况下的类分数计算如下:
最后,将各字典下各类的识别得分求和,得出最终得分值,并将测试样本归类为分值最高的类。
2 实验
2.1 AR数据库
为验证算法性能,在数据集AR上进行测试,并与时域LBP算法(SLBP_CRC)、频域LBP(FLBP_CRC)算法作对比。
首先在AR数据库上测试各算法的性能,选择前1~30人的每人13张图像作为通用训练集,其余90人从V1~V7中选择一张图像作为训练样本。测试分为如下3种情况:
(1)无遮挡情况下每人选取前7张照片中除训练样本外的其余6张作为测试样本,即测试样本数量为90×6=540;
(2)每人选取3张墨镜遮挡图像作为测试样本,即测试样本数量为90×3=270;
(3)每人选取三张围巾遮挡图像作为测试样本,即测试样本数量为90×3=270。
每组实验分别选取不同的样本作为训练样本,运行7次,计算平均结果作为最终的测试结果,见表1所列。
从表1的结果可以看出,与ESRC算法及SAE特征相比,本文算法联合空频域并融合深度自编码网络提取的特征可有效提高算法的识别率。图3记录了不同训练样本下本文算法的识别率,可以看出,当训练样本为每类的V3时,识别率均下降,而将每类的V5作为训练样本时,识别率较高。观察V3,V5样本可以发现,与其他样本相比V3样本中眼睛张开程度较小,V5则更接近自然状态下的样本。V2和V4也含有表情变化但大部分表情信息体现在嘴部变化,由此可知眼睛在人脸识别中包含重要的判别性信息。口罩遮挡的识别率明显低于墨镜遮挡的识别率,说明遮挡比例过大时人脸判别性信息丢失较为严重。
与ESRC算法相比发现本文在墨镜遮挡识别情况下可有效提高算法的识别率,说明本文算法能够有效提取眼部之外的信息。而其他两种情况下,相比于ESRC算法,本文算法的识别率亦有大幅提高。AR数据库上不同训练样本下本文算法的识别率如图4所示。
为进一步分析本文算法与ESRC算法性能,本文将两种算法的运行时间进行比较,发现本文算法的运行时间远低于ESRC算法的运行时间。因SAE网络可利用通用训练样本集提前训练好,因此本文不考虑SAE网络的训练时间。不同训练样本下,本文算法与ESRC算法运行时间如图5所示。
2.2 PIE数据库
PIE数据库包含68个人5种视角下的人脸图片,每个视角下的图像还包含光照及表情变化,姿势1共包含49张图像,姿势2共包含24张图像,姿势3共包含24张图像,姿势4共包含49张图像,姿势5共包含24张图像。部分PIE实例如图6所示,可见该数据库进行人脸识别测试面临的主要挑战是姿势变换,其次为光照及表情变化。
[14] LU J,TAN Y P,WANG G. Discriminative multimanifold analysis for face recognition from a single training sample per person [J]. IEEE transactions on pattern analysis and machine intelligence,2013,35(1):39-51.
[15] ZHANG D,CHEN S,ZHOU Z H. A new face recognition method based on SVD perturbation for single example image per person [J]. Applied mathematics and computation,2005,163(2):895-907.
[16] GAO Q X,ZHANG L,ZHANG D. Face recognition using FLDA with single training image per person [J]. Applied mathematics and computation,2008,205(2):726-734.
[17] WANG J,PLATANIOTIS K N,LU J,et al. Venetsanopoulos,On solving the face recognition problem with one training sample per subject [J]. Pattern recognition,2006,39(9):1746-1762.
[18] DENG W,HU J,GUO J. In defense of sparsity based face recognition [C]// Proceedings of CVPR,2013:399-406.
[19] JI H K,SUN Q S,JI Z X,et al. Collaborative probabilistic labels for face recognition from single sample per person [J]. Pattern recognition,2017,62:125-134.
[20] ZHANG P,YOU X,OU W,et al. Sparse discriminative multi-manifold embedding for one-sample face identification [J]. Pattern recognition,2016,52:249-259.
[21] GOTTUMUKKAL R,ASARI V K. An improved face recognition technique based on modular PCA approach [J]. Pattern recognition letters,2004,25(4):429-436.
[22] CHEN S,LIU J,ZHOU Z H. Making FLDA applicable to face recognition with one sample per person [J]. Pattern recognition,2004,37(7):1553-1555.
[23] YAN H,LU J,ZHOU X,et al. Multi-feature multi-manifold learning for single-sample face recognition [J]. Neurocomputing,2014,143:134-143.
[24] ZHU P,YANG M,ZHANG L,et al. Local generic representation for face recognition with single sample per person [C]// Proceedings of ACCV,2014:34-50.
[25] L F ZHOU ,Y W DU,W S LI,et al. Pose-robust face recognition with Huffman-LBP enhanced by divide-and-rule strategy [J]. Pattern recognition,2018,78:43-55.
[26] AHONEN T,HADID A,PIETIK?INEN M. Face description with local binary patterns:application to face recognition [J]. IEEE trans. pattern anal. mach. Intel,2006,28(12):2037-2041.
[27] KAVOUSIANOS X,KALLIGEROS E,NIKOLOS D. Optimal selective Huffman coding for test-data compression [J]. IEEE trans. comput.,2007,56(8):1146-1152.
