基于隐私保护的央行数字货币监管审计架构*
2019-12-11陈逸涛周志洪陈恭亮
陈逸涛,周志洪,陈恭亮
(上海交通大学,上海 200240)
0 引 言
自比特币[1]诞生以来,基于区块链技术的电子货币受到了强烈关注。区块链为人们构建了一个理想的无中心的开放自治系统。通过一系列的底层密码学的组合构建其有效的哈希链,从而形成了初步的信任链和监管链,而合理的激励机制和有效的共识机制,能不断维持该信任链,人们可以在基于规则的前提下实现金融货币体系的自我管理。基于区块链的电子货币系统是经济学家眼中理想的货币和金融系统。
但是,当前货币体系中铸币发行和交易支付中存在显著的边界,而该边界的存在是国家对于货币管理的体现。为此,RSCoin[2]提出了双层链架构,在无法短时间消除该边界的前提下保留其边界,通过双层链机制上层为投放清算链实现其铸币投放及其央行对各个商业银行和其他金融机构的清算管理,下层链构建其传统的交易网络,从而构筑其央行可管理的电子货币体系。但是,当前双层链的监管虽然可以做到有效的公开验证,但是却以隐私保护的缺失作为代价——通过公开所有交易使其参与者能够验证其完整性和正确性。这对于诸如交易咨询机构等,依赖于保密决策的金融服务机构。同时,对于需要遵循类似GDRP[3]的相关数据隐私法律法规的组织也是不可容忍的。
央行数字货币作为法定数字货币,在流通和发行的过程中必然要做到在确保用户隐私的前提下实行其高效和安全的监管,做到对于违法交易的有效审计。而当前的对现有电子货币的监管审计架构并不能对双层链的央行数字货币形成有效监管,故探索一种可行的基于隐私保护的对于央行数字货币的监管和审计架构迫在眉睫。
本文对于央行电子货币的双层链架构,探索性地提出了其安全有效的监管和审计机制。利用承诺机制,本方案确保了交易内容的隐匿性;采用零知识证明,使其交易网络的参与者可进行公开验证来确保交易的正确性;对于需要审计的交易记录,本方案使用基于两方的门限Paillier[4]加密方案实现了其无需可信设置的审计功能。
1 预备知识
1.1 双层链
双层链是首先由RSCoin提出的央行电子货币方案,可以有效分离央行的发币功能和商业银行或者金融机构的交易功能,同时利用其公开账本的性质实现其公开验证的监管和审计功能。本方案在下层链中不再使用其RScoin的两阶段共识机制,而是采用传统区块链的分布式账本架构。本方案注重于双层链的监管和审计,所以其双层链的模式有如下定义:下层链可以使用多中心或者无中心的分布式账本模式,商业银行的用户账户对应于每一个用户i;上层链每个商业银行对应于央行有其相应的银行账户,如图1所示。
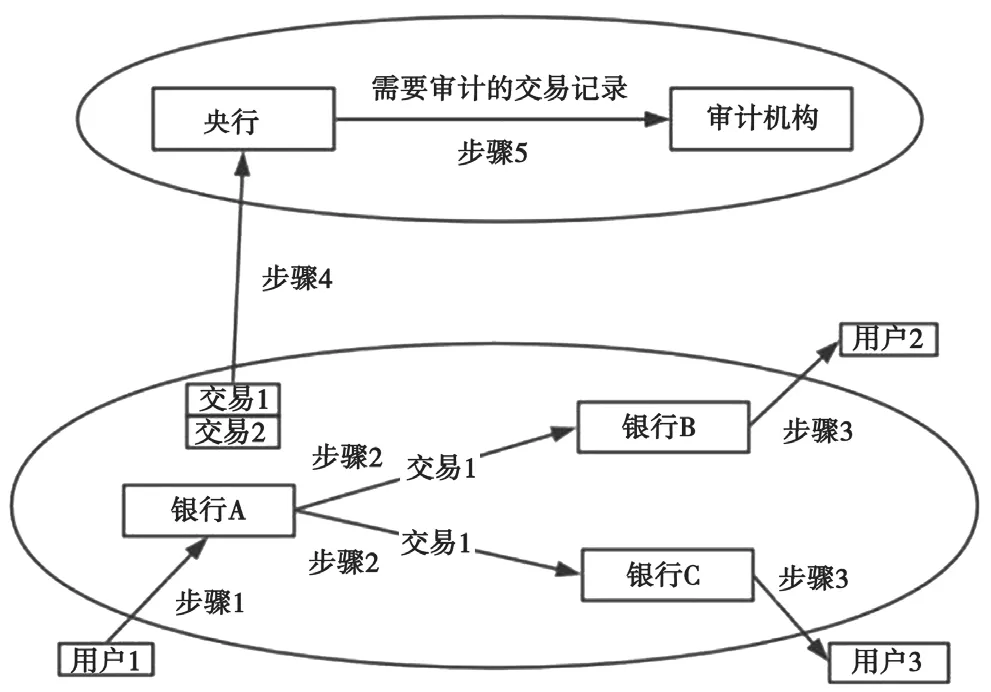
图1 双层链架构
步骤1~步骤3:用户1发起交易请求,将金额v1分别转入用户2和用户3对应的商业银行账户,其金额分别为v2和v3。交易在其他验证者处进行有效验证,并且获取其共识签名,记录于公开账本中。
步骤4:在上层链央行获取从下层链中获取其记录于公开账本中的交易集,并进行相关的验证。央行在初始阶段根据其法币的发行量,为其商业银行确定其初始的银行账户额度,作为其上层链的初始UTXO交易,并根据从下层链中获取的交易集获得商业银行账户的资产变动情况。上层链同样可以是一个多中心的区块链架构,多个清算行从下层链中获取交易集,之后经由共识算法形成上层链的公共账本,然后央行从其公开账本中获取各商业银行的资产变动情况。
步骤5:需要审计时,审计机构从央行获取需要审计的交易记录和交易相关商业银行的银行账户信息。
1.2 密码学假设
定义1(DDH假设):群G是一个阶为素数p的循环群,独立随机选取整数a,b,c∈Zp和生成元g∈G对于任意PPT敌手A,存在如下关系:
|Pr[A(g,ga,gb,gab)=1]-Pr[A(g,ga,gb,gc)=1]|≤ negl(λ)(1)
其中negl为可忽略函数,λ为安全参数。
定义2(DCR假设):设p、q是两个大素数N=pq,独立随机选取r∈ZN和y∈Z*N2。对于任意PPT敌手A,存在一个可忽略函数negl(λ),λ为安全参数,使其满足关系:

1.3 基于两方的门限Paillier加密系统
本方案采用的两方的门限Paillier加密算法(TPS)在文献[4]中有详细说明。在本方案中,假设p0为交易发起者及其相关交易方,p1为审计机构,有以下4个多项式时间算法:

DKeyGen(1λ):分布式生成RSA的合数N=pq,且不泄露其合数的分解因子p和q,其输入是安全参数λ,输出为参与方共同计算出来的RSA合数N。
Dsk(N,sk0,sk1): 输 入 是 DKeyGen(1λ)生 成 的RSA合数N,输出为参与者的密钥共享分片d0和d1。其中,输入的sk0和sk1为p0和p1根据其DKeyGen生成的RSA合数N时产生的分解因子p和q的部分分量pi和qi,i∈{0,1},各自生成sk0=N-p0-q0+1,sk1=-p1-q1, 其 输 出 d0和 d1满 足d0+d1=d≡1modN,d≡0mod φ(N),从而确保参与者的私钥生成是根据DKeyGen算法正确生成的。
Enc(N,m,r):输入消息m,随机均匀选取随机数r∈ZN以及Paillier的公钥N,输出为Paillier加密所产生的密文c。Paillier加密是IND-CPA安全的,其任意PPT敌手都不能通过密文来获取相关的明文m的信息。
Dec(c,d0,d1):输入为Paillier的加密密文c以及p0和p1的密钥共享分片d0和d1,输出为明文m,p0计算其明文分量c0=csk0modN2,将其c0和对d0的承诺值发送给p1,同时p0发送其proof可以使其审计机构验证其身份保证其sk0的正确性;之后p1自己计算cd1并验证c=cd0·cd1成立,同样p1也计算其明文分量c1=csk1modN2,对于d1的承诺值和sk1的zkproof,将其发送给p0验证p1的身份,之后p0和p1都可以计算明文m=((c0·c1)modN2-1)/N。由于p0知道c的解密明文,可以进一步验证p1私钥和解密的正确性。
1.4 零知识证明
为了对抗其恶意敌手,且在不公开私有信息的前提下做到公开验证,本方案中需要采用如下的零知识证明:
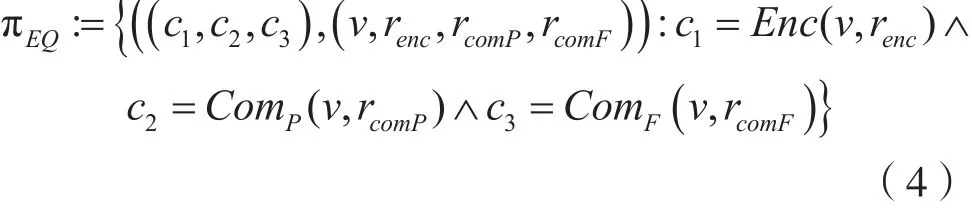
验证其交易发起方使用Paillier加密的值c1和交易发起方的Pedersen承诺c2中的被承诺值相等,在其后的证明中由于这两者直接证其不满足soundness需要fujisaki承诺c3来作为证明桥梁:

验证交易发起方的Pedersen承诺中被承诺值大于等于0:
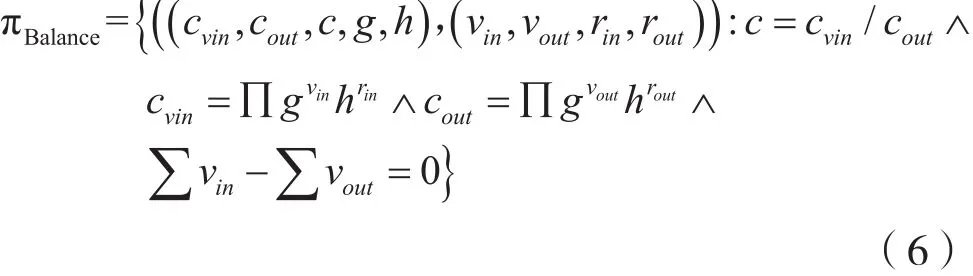
验证其交易的输出值的总和与输出值相等。
2 监管设计
由于本方案是基于双层链锁建立的监管审计架构,所以在监管方面,对于下层链能使其在其保护交易内容的前提下实现对交易合法性的有效监管,必要时在下层链可以进一步隐藏交易图——隐藏交易发起者的身份,但其仍能保持交易监管的有效性。对于上层链,央行为其主要的监管方,央行需要验证从下层链中获取交易集的合法性,同时确保银行账户的正确性——防止银行账户出现负数,确保其金融市场的正常资金流动
2.1 监管机制概况
方案中对应的下层链可以是一个多中心的区块链交易网络,承载着用户的所有交易账本。在本系统中定义就如同在比特币中的交易定义,交易tx即交易发起方通过广播该交易并使用共识机制使其UTXO的所有权发生变化,形成商业银行之间的资金流动。该下层链的交易系统参与者包括交易tx的发起方和交易tx内容的接受方。对于该交易网络中其他未参与方,对该交易通过零知识证明验证、签名以及哈希的验证,对其交易的合法性、完整性进行相关验证。
2.2 交易中的监管构成
方案中对于下层链的商业银行并未假设其交易行为永远是诚实的。它假设这些商业银行存在着企图操纵账户偷取或者隐匿资产的可能性,同时这种假设也同样适用于上层链的央行和其他清算机构。基于以上考虑以及对于隐私的保护,本方案采用Pedersen承诺协议,隐藏同时绑定其交易值。Pedersen承诺具有统计意义上的隐藏性,即对于任意计算能力的敌手都不能仅从承诺值中猜测出被承诺值。同时,Pedersen承诺具有计算意义上的绑定性,即对于任意多项式敌手其不能在不更改承诺的条件下实现对被承诺值的更改。绑定性同时也意味着交易中资产不可被随意增加或减少。
对于关于资产的交易有如下定律:(1)为确保被确认的交易的不可变性,在交易中流动资产不能被任意增加和减少,可知基于Pedersen承诺的绑定性可以得到有效保障;(2)交易的合法性,即要保证被确认交易中的各个资产的值始终大于等于零,交易发起方的账户有足够的金额完成该笔交易的转账流程。这个在公开账本中可以通过检查交易内容和查看历史交易的方式实现,但是对于方案中由于交易内容通过Pedersen承诺进行了隐匿处理,所以对于交易合法性的检验必须通过一系列零知识证明来完成。具体来说,对于监管本方案使用proof L1∧ L2∧ L3。
2.2.1 Proof L1(πBalance)
式(7)用于检验对于一个交易的输入总和与输出总和是否完全相等,也确保了交易中的交易相关资产在总额上的不可变更性,是资产安全性的一个重要体现。

对于该proof通常采用sigma-proof[5]。proof生成过程如下。
公共输入:所有输出和输入的Pedersen承诺值Cin和Cout,对于所有Pedersen承诺,从阶数为大素数p的循环群G中独立随机选取其生成元g∈G和h∈G,对于任何人其loggh都是不可知的。
私有输入:构成Pedersen承诺的被承诺值vin、vout和其所选的随机数rin、rout。
步骤1:Prover随机选取rvin,rvout,rrin,rrout,r0∈ℤp,计 算 αvin=grvinhrrin,αvout=grvouthrrout,α0=hr0, 将 αvin、αvout、α0发送给 Verifier。
步骤2:Verifier均匀随机选取challenge e。
步 骤 3:Prover计 算 fvin=rvin+e·vin,fvout=rvout+e·vout,frin=rrin+e·rin,frout=rrout+e·rout,f0=r0+e·(rin-rout), 并 将 fvin、fvout、frin、frout、f0发 送给Verify。
Verify 验 证 gfvinhfrin=αvin·(Cin)e、gfvouthfrout=αvout·(Cout)e和hf0=α0(Cin/Cout)e这 3个等式是否成立。
此为sigma-proof交互式的证明过程,在公开账本中需要使用非交互式证明,这里可以采用Fiat-Shamir变换[6]将交互式证明转换为非交互的证明
Proof L2用于检验其交易中被承诺的交易资产数量始终为正,确保交易的安全性。对于输出金额账户和输入金额账户,确保不会因为出现负数而发生在一次交易中输出账户出现资产增加而输入账户出现资产减少的情况。直接采用Bulletproof[7]证明去交易的金额值大于等于零,这是因为Bulletproof所生产的proof的size相比传统的范围证明小,达到了O(log(n)),极大地减少了交易tx的size大小,且bulletproof相比与其他范围证明如基于Borromean环签名[8]的范围证明其无需可信设置。这个特性使其更加适用于诸如保密交易[9]的公开验证。
2.2.3 Proof L3
同L2相同,也是采用range Proof;与L2不同,L3需要证明其发起交易方交易发起的合法性,即下层链的商业银行有资金来推动此次交易的生成,这是商业银行向上层央行和清算机构的证明。由于央行在商业银行加入下层链的交易网络时根据实际的法币发行和流通量给与商业银行一定的储备金,下层链交易发生时,交易发起者的商业银行应始终保证其有足够的资金发起,不去恶意创造资产。由于链上的数字货币有其国家作为保证可以以一定比例进行交换,所以下层商业银行创造资产会造成通货膨胀,影响国家经济。一个简单的想法即由于上层链中对于每个商业银行账户、央行和清算机构有其最初为其分配的储备金的Pedersen承诺,由于Pedersen承诺的隐藏性,该承诺值对于下层链的所有商业银行是公开的,且央行和清算机构会根据其从下层链获取的交易集通过Pedersen承诺的同态性,在不公开资金的情况下,根据交易中的输入和输出定时变更各个商业银行的储备金。由于各个其承诺值是公开的,上层链从下层链获取的交易集对于各个商业银行也是可知的,所以央行只能根据获取的交易集变更储备金,从而杜绝央行恶意变更商业银行资产的行为。
对于该证明,可以通过证明在上层链中当前储备金的range proof来证明。但是,考虑到上层链的储备金并不是实时变更,所以该证明中还需要加上下层链中与交易发起者相关的被认可的交易的储备金的承诺值。在上层链从下层链收取交易的间隔,可以视作上层链对其各个商业银行的账户进行锁定时间,未进入上层链的交易,但是与需要证明交易的发起方相关的交易称之为挂起的交易。对于本方案来说,由于上层链会定时收取下层链的交易,所以无需人为刻意去对其进行处理,但是每次上层链获取交易时必须按照交易的先后顺序放入上层链(在时间服务器同步的情况下,可以根据时间戳进行判断),同时在交易发起方生成相关零知识证明时,需要将所有与交易发起方所在的商业银行账户相关的挂起的交易都考虑到其零知识证明中。
3 审计设计
3.1 审计机制概况
定义审计:央行在交易监管时针对某一可疑交易向审计部门提出审计请求,审计部门解密交易中被加密的交易资金的密文。在本方案中,交易发起方采用Paillier加密系统加密交易资金。由于Paillier加密保证其在没有私钥的情况下,任意多项式时间敌手都不能分辨密文。同时,与Pedersen承诺进行绑定,通过零知识证明保证其Pedersen承诺的被承诺值与被加密值相等。对于解密,通过分布式可验证的密钥分享策略,使其监管方在整个审计流程中始终不能获取完整的私钥,而需要被审计的交易相关利益方不能使用其错误的解密密钥进行部分解密操作。
3.2 交易中的审计构成
为了实现审计功能,方案采用Paillier加密和密钥分享策略。在下层链的tx交易中,对交易的各方使用其各自公开的Paillier公钥进行输入和输出金额的加密。同时,为了实现完成其审计功能,对于上层链在监管方面只隐藏交易内容,我们在使用央行的公钥,对其输入和输出交易方的身份ID进行加密。这里只需确保其身份ID在解密前外不任意人知晓和更改,这里可以采用IND-CCA2安全的加密策略即可。如果下层链不需要隐藏交易图,也可以在交易中直接公开。
审计功能实现的关键在于用于审计的Paillier加密和用于监管和隐藏的Pedersen承诺需要进行相关的绑定,即要保证其被承诺值和被加密值相等。Douglas在混淆证明论文[10]中,提出其Paillier加密和Pedersen进行绑定proof需其fujisaki承诺[11]作为中间桥梁,因为Paillier加密是基于RSA的二次剩余假设,所以对于公钥N的分解因子是未知的,而传统的Pedersen承诺是一个基于已知素数的模来进行运算的,直接证明其soundness无法满足。以下是对其相关的零知识证明,方法与文献[12]类似,即proof L4:
孝文化是中国传统道德的核心,是大学生人格修养中必须恪守的伦理规范。孝道的核心价值在现代社会仍然发挥着不可估量的作用。它在维护家庭和社会稳定方面的作用不容忽视。《孝经》中提出“身体发肤,受之父母”,引导大学生在人格修养中,首先要爱惜自己的身体,尊重生命。其次,孝的内涵从“善事父母”的家庭责任和义务出发,开始由家庭伦理泛化到处理人与人之间关系的社会伦理道德规范,形成多重的文化内涵,甚至上升为国家意识形态,渗透于社会生活的方方面面,比如当今社会推崇的敬老、爱老、养老风气仍然在大学生人格修养中得到继承和发扬。

Paillier的公钥为N,Pedersen承诺中的模为p在本方案中取安全素数q,满足q|p-1。
步骤1:Prover随机选取d∈Z2l+2k,l为其v的大小,k为安全参数,之后选取Prover计 算Z=g3dh3rzmod p,并将其X、Y、Z、Ce、Cp、CF发送给Verifier。
步骤2:Verify均匀随机选取e,将其发送给Prover。
步 骤 3:Prover计 算 f=d+e·v,fx=rxere,fy=ry+e·rF,fz=rz+e·rp, 将 f、fx、fy、fz发 送 给Verifier验证:

如果f在其范围内且3个等式成立,则接受proof L4;否则,拒绝。
为确保审计的正确性,本方案采用文献[4]的分布式RSA合数N生成算法DKeyGen,保证其生成的合数不偏向任何一方。同时,采用Dsk算法生成可以验证的分布式私钥,在其解密时遵循Dec算法进行相互认证,并通过零知识证明确保各自提交的解密密文使用的明文分量时使用的解密密钥是正确的。文献[4]提供的是基于两方的门限分布式Paillier加密算法,对多方进行审计时也可以使用其PVSS[13]作为可验证的密钥共享方案。文献[14]提供了使用PVSS的门限Paillier加密算法。
4 安全性分析
回顾交易的监管和审计构成,其交易的构成如下:

其中Comp(v)是对v的Pedersen承诺,Enc(ID)为使用央行的公钥对其输入输出交易方的身份ID的加密密文,ComF(v)是对v的fujisaki承诺,Encp(v)为对v的Paillier加密密文L1,L2,L3,L4在第2节和第3节的零知识证明,σtx为其交易发起方对于该交易的签名。从交易结构中可以清楚了解,Pedersen承诺保证了交易内容的隐匿性和绑定性,通过L2范围证明保证其输入和输出的合法性,通过L3保证整个交易的合法性,L1保证交易发起方发起交易的合法性,而L4保证了审计所需的加密密文与其交易中的Pedersen承诺是相关的。对于签名,则进一步确保了整个交易环节中交易的完整性和不可篡改性。方案由于在交易中使用了央行的公钥对其交易方的身份ID进行加密,故对于上层链其交易图是不隐藏的,同时对于下层链使用环签名进行交易图的隐藏。由于上层链只要确保央行不对其进行公开,下层链的各个节点是无法知道其历史交易的交易相关方的身份。方案中由于审计需要解密,故将此操作放在链下,同时审计双方在事先使用PVSS或者基于两方的可验证密钥共享策略和分布式解密,实现其公开可验证的无需可信设置的审计方案,且在双方未泄露各自私钥的前提下,审计机构无法独立获取被审计的交易的具体信息。
5 结 语
本文提出了一种基于隐私保护前提下的央行数字货币监管审计架构,确保了双层链架构的央行数字货币的安全性、隐私保护性和可监管审计性。在隐私保护和可监管性的考量下,对于监管仅需要对于上层链形成交易内容的隐藏,而在下层链不仅可以实现对交易内容的隐藏,也可以根据需求选择性实现对交易图的隐藏,从而保证其央行电子货币在交易链上的隐私受到保护。对于监管,使用其Pedersen承诺保证交易内容的隐藏和不可更改性,同时采用零知识证明确保交易的正确性和交易发起方发起交易的合法性。对于审计,采用可验证的密钥共享算法和基于门限的Paillier加密算法,确保审计者和被审计者都能正确执行审计流程,保证审计的正确性。审计私钥的分片确保了审计机构的审计行为不会破坏其他交易的隐私保护的特性,同时审计者和被审计者通过零知识证明验证了各自的审计私钥也有助于确认双方的身份。对于具有隐私保护特性的保密交易的Front-running问题,本文只是基于理想共识,在上层链交易集收取的基础上进行了简单处理,但是基于实际的共识机制的处理还需做进一步的深入研究。
