融合多层卷积特征的鲁棒相关滤波跟踪*

贾 惠，齐苏敏，王来花，姜世浩

（曲阜师范大学 软件学院，山东 曲阜 273100）

0 引 言

目标跟踪是在视频第一帧给定目标的初始位置，之后预测目标在视频后继帧的位置，是计算机视觉领域中底层的核心技术[1]。近年来，基于相关滤波的跟踪算法表现较好，在保证跟踪精度的同时，极大地提高了跟踪速度，引起了领域内专家学者的广泛关注。相关滤波的原理是在跟踪场景中，对目标产生高响应，对背景产生低响应。自2010年Bolme等人首次将相关滤波应用于跟踪领域提出误差最小平方和滤波算法MOSSE[2]以来，出现了许多经典的相关滤波算法，如CSK[3]、KCF[4]、DSST[5]等算法。但是，这些相关滤波跟踪算法采用方向梯度直方图HOG[6]、颜色名称CN[7]等浅层特征，具有较强的针对性，难以捕捉目标的语义信息，当目标发生较大的外观变化时，易受到形变、遮挡、复杂背景等不利影响而跟踪失败，即跟踪的鲁棒性不高。

随着深度神经网络的发展，研究人员尝试将深度特征应用于目标跟踪。2015年，Danelljan等人提出DeepSRDCF[8]算法，将SRDCF[9]中的HOG特征替换为CNN中单层卷积层的深度特征，极大地提升了效果。同年，Ma等人利用预训练好的卷积神经网络提取深度特征，提出了基于分层卷积特征的跟踪算法HCF[10]，通过将来自卷积神经网络的多层卷积特征进行融合，提升了跟踪算法的性能。2016年，Danelljan等人提出了CCOT算法[11]，融合了不同分辨率的特征图，解决了卷积神经网络不同卷积层分辨率不一致的问题。2017年，Danelljan等人提出了ECO算法[12]，在CCOT的基础上针对模型参数过多、训练样本数量过大以及模型更新策略等问题做出了改进，进一步提升了跟踪性能。2019年，Dai等人提出ASRCF[13]算法，在传统相关滤波器的基础上加上自适应空间正则，学习特定对象的有效空间权值及其外观变化，从而在跟踪过程中获得了更可靠的滤波系数，同时基于浅层特征估计目标尺度，在深度特征层上定位目标。

上述相关滤波跟踪算法中，只采用浅层特征的目标跟踪和只采用深层特征的目标跟踪都不能达到最佳的跟踪效果。2018年，Danelljan等人证明[14]，浅层特征能够为目标跟踪提供精确性，深层特征能够为目标跟踪提供鲁棒性，二者的融合能够提升跟踪效果。因此，本文提出了基于VGG-Net[15]网络的多层卷积特征融合的目标跟踪算法，在DSST算法框架下，提取VGG-Net网络3个卷积层的特征，并分别训练相关滤波器，将每层响应加权融合，响应值最大的位置即为预测的目标位置。在OTB2013的实验结果表明，本文算法在一些具有挑战性的场景下不仅能保证良好的跟踪精度和鲁棒性，而且能保持较快的跟踪速度。

1 相关工作

1.1 VGG-19网络模型及其卷积特征

VGG-19网络模型是在ImageNet[16]数据集上训练得到的。通过3×3的小型卷积核和2×2的最大池化层的反复堆叠，构建了19层的卷积神经网络。该模型包含5组卷积层和3个全连接层，网络结构如图1所示。VGG-19网络模型证明了几个小滤波器（3×3）卷积层的组合优于一个大滤波器（5×5或7×7）卷积层，通过不断加深网络结构可以提升模型的整体性能。在VGG-19网络模型提取的所有特征中，可以用于相关滤波跟踪的只有卷积层和池化层的输出。因此，本文算法去掉3个全连接层，降低了参数数量，缩短了训练时间，利于目标跟踪的实时性要求，同时提取的卷积特征仍能满足目标跟踪的准确性与鲁棒性要求。

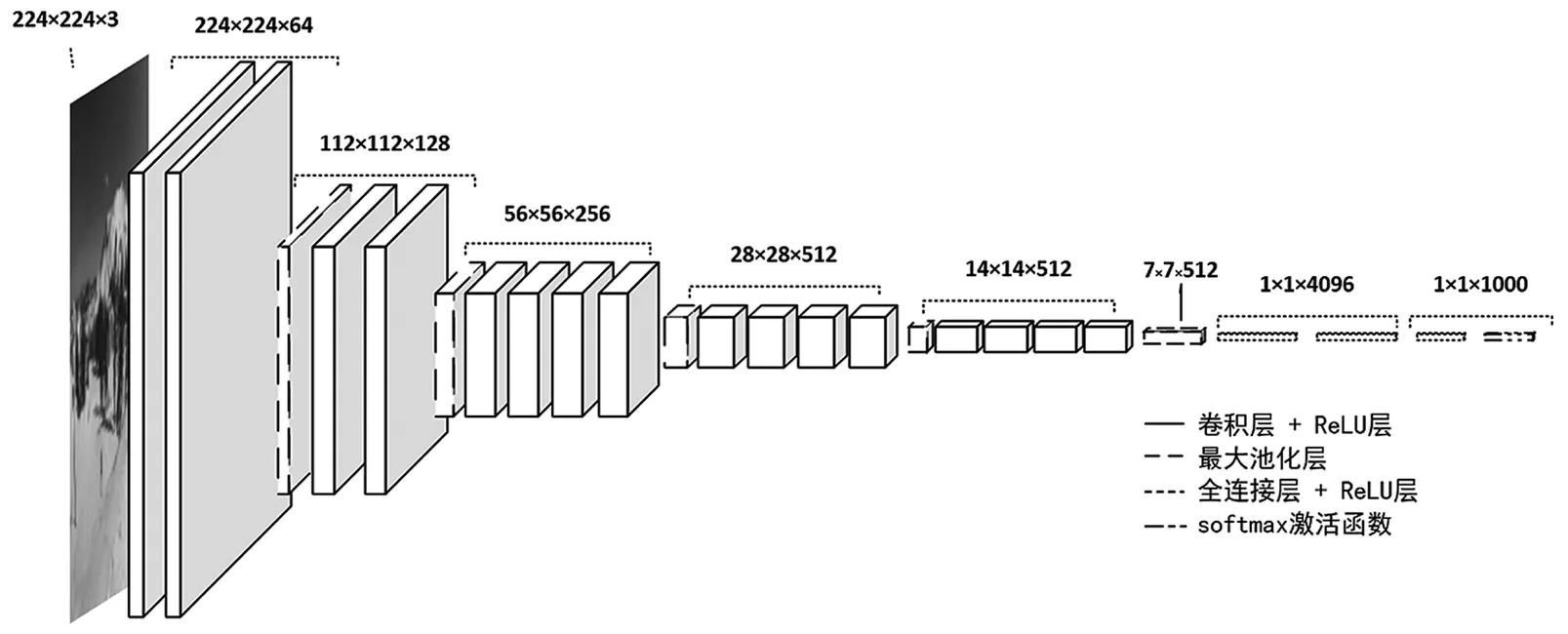
图1 VGG-19网络结构

在VGG-19网络模型中，随着卷积层深度的增加，空间分辨率逐渐降低。过低的空间分辨率不能实现准确的目标定位，但是通过使用双线性插值可以将每个特征映射调整为固定的较大尺寸来解决这个问题。令h表示特征图，x表示上采样后的特征图，i代表位置，插值权重α取决于i和k邻域的特征向量，第i个位置的特征向量为：

图2显示了给定输入图像对应的每一组卷积层的最后一层输出的特征图。可以看出，网络层次越浅，卷积特征的分辨率越高，含有的空间特征和纹理信息越丰富。网络层次越深，特征分辨率降低，已经很难看到细节，但是包含了目标的高级语义信息，能够表示目标的深层特征，对尺度、旋转等形变具有较强的鲁棒性。

图2 VGG-19模型不同卷积层的特征可视化

1.2 相关滤波跟踪

相关滤波跟踪的工作流程为：

（1）在视频的初始帧，以目标位置处的图像块提取多通道特征，训练相关滤波器。设跟踪目标的多通道特征图为x=[x1,x2,…,xd]∈RM×N×D，其中M、N和D分别表示特征图的宽度、高度和通道数。通过矩阵的循环移位操作做密集采样，每个训练样本xm,n(m,n)∈ {0,1,…,M-1}×{0,1,…,N-1}具有高斯函数标签ym,n，通过求解下面的最小化问题构造相关滤波器w*：

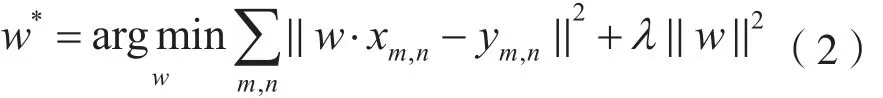
通过傅里叶变换（Fast Fourier Transformation，FFT）将相关滤波器w*从时域变换到频域，则滤波器W*在第d个通道的频域表达式为：

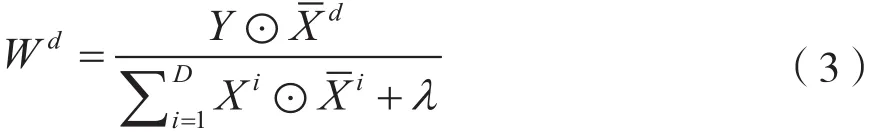
（2）在随后的每一帧，根据前一帧中预测的目标位置提取新的图像块的特征zd，并通过余弦窗弱化图像边缘对跟踪结果的影响。

（3）使用傅里叶变换后的特征Zd与滤波器Wd进行相关操作得到响应值f，最大响应值所在的位置即为预测的目标位置：

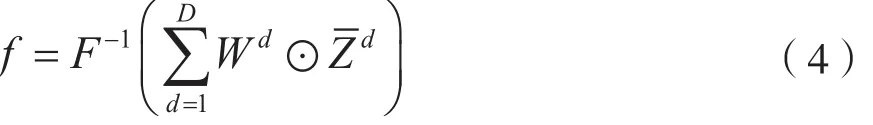
（4）在预测的目标周围截取S个不同尺度的图像块提取其特征图，组成新的特征z，同样求取每一维度的傅里叶变换得到Zd，使用式（4）计算相关性得分，最大值所对应尺度为最终的估计尺度。

（5）依据预测的目标位置、尺度提取特征，分别更新平移和尺度相关滤波器，重复上述步骤至跟踪结束。

2 融合多层卷积特征的相关滤波跟踪

本文算法流程如图3所示，分为4个部分。

（1）将视频序列第一帧中给定的目标位置处的图像输入到深度网络模型VGG-19中，提取conv1-2、conv3-4和conv5-4的特征图，筛选出有效的卷积特征，进行训练并初始化相关滤波器。

（2）对于第t帧输入图像，以第t-1帧图像中的预测结果为中心确定搜索框，使用VGG-19网络模型获取搜索框内需要的卷积层的特征。

（3）使用从不同层训练得到的滤波模版进行运算，得到不同的置信图，将每层响应加权融合，确定最终目标位置，再通过尺度滤波器估计当前目标的最佳跟踪尺度。

（4）根据第t帧中估计的目标位置，提取图像块用于相关滤波器的更新。

2.1 特征选取

神经网络的卷积特征具有手工特征无法实现的特性。原理上看，卷积操作是在输入图像上做滑动滤波，具有位移不变性，不具备尺度和旋转不变性。但是，神经网络的池化操作使得高层特征具有了尺度和旋转不变性。因此，在目标跟踪中，既需要浅层特征区别目标类内差异，也需要高层特征区别目标类间差异，充分利用不同卷积层特征的优势，融合卷积层的多层特征实现准确和鲁棒的目标跟踪。如图3所示，通过实验对比本文选取了3层卷积层用于提取目标特征，分别为较浅卷积层conv1-2、较深卷积层conv3-4以及最后一层卷积层conv5-4。

此外，卷积特征为多通道特征，但不是每一个通道的特征都是有效特征，也可能对跟踪过程贡献较小。如果使用这类特征进行跟踪，并不能提高跟踪效果，反而会降低跟踪速度。因此，为了满足跟踪的实时性要求，需要筛选卷积特征，去除无效特征。例如，VGG-19模型中conv5-4层的特征是一个14×14且包含512个通道的特征图，使用如式（5）所示的方差筛选特征：每一层按照方差大小选择前256个通道的卷积特征，由此去除冗余特征通道，提高跟踪算法的速度。

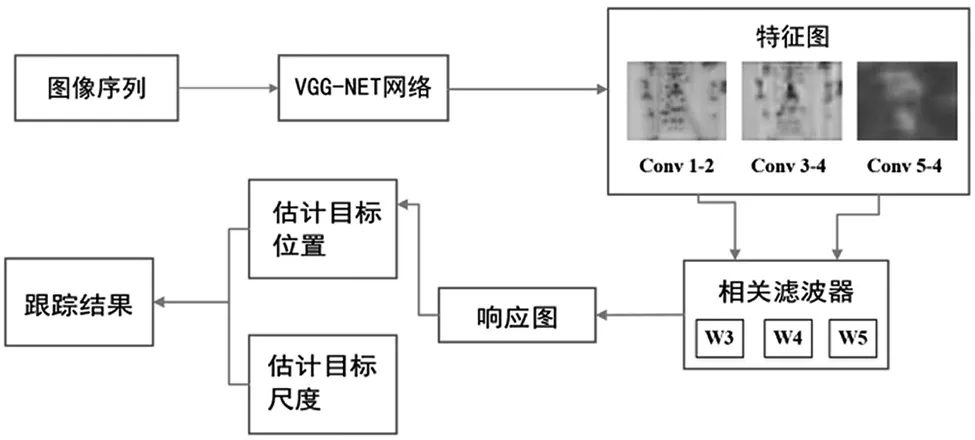
图3 跟踪框架

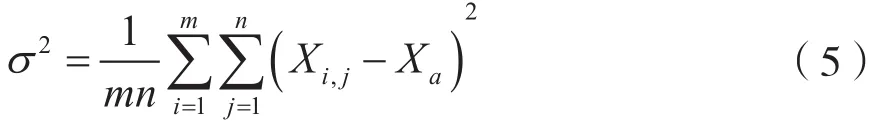
其中，m、n分别代表每一层特征图的长、宽，Xi,j表示特征图在某一通道的特征值，Xa表示对当前通道特征取平均值。

2.2 模型更新

在给定目标外观训练样本的情况下提供最佳滤波器。理论上需要计算最佳响应位置的一个d×d线性方程组来学习鲁棒的相关滤波器，但是这对于在线目标跟踪来说计算量过大、实时性较差。卷积特征的通道数目通常较多，为了获得鲁棒逼近，分别更新式（3）中相关滤波器的分子At和分母Bt：

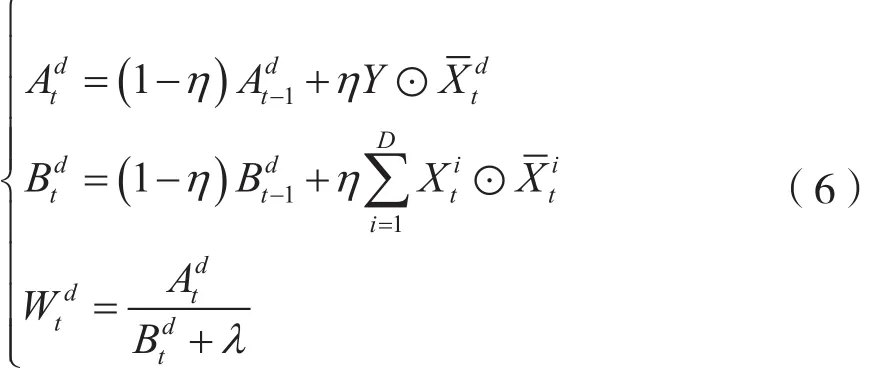
式中，t为帧序列；η为学习率，表示目标外观对新帧图像的学习能力。

2.3 算法实现

在跟踪过程中，以前一帧目标位置为中心获取搜索窗，对裁剪出的图像块提取特征作为测试样本，测试样本与前一帧滤波器求相关响应，根据最大响应值定位目标位置。算法在更新时采取与跟踪同样的方式提取训练样本，使用训练样本与高斯标签函数更新滤波器。本文算法在第t帧的跟踪流程如表1所示。

3 实验结果与分析

3.1 实验环境、参数及评估指标

本文算法开发环境为Matlab R2015b以及深度学习库 MatConvNet，硬件配置为Intel（R） Xeon（R）Gold 6130 CPU @ 2.10 GHz（2处理器），96.00 GB内存。实验中对测试视频采用相同的参数，具体设置为：第1、3、5层中卷积特征所占权重分别设置为1、0.5、0.02，正则化参数λ=10-4，尺度步长α=1.02，尺度数量S=33，学习率η=0.01。

选取来自OTB2013[17]标准测试数据集的50个视频对算法进行测试。在这些测试视频中，包含的挑战有11种，分别为突然运动（Fast Motion，FM）、背景混乱（Background Clutters，BC）、变形（Deformation，DEF）、遮挡（Occlusion，OCC）、运动模糊（Motion Blur，MB）、光照变化（Illumination Variation，IV）、尺度变化（Scale Variation，SV）、出视野（Out-of-View，OOV）、低分辨率（Low Resolution，LR）、 平 面 外 旋 转（Out-of-Plane Rotation，OPR）和平面内旋转（In-Plane Rotation，IPR）。实验针对上述挑战做出性能测试。

3.2 定量分析

通过与5个具有代表性的跟踪器进行比较来评估所提出的算法，分别为基于相关滤波的CSK[3]、KCF[4]、DSST[5]、Staple[18]以 及 基 于 深 度 学 习 的ECO[12]。通过空间鲁棒性评价（Spatial Robustness Evaluation，SRE）对算法进行测评。首先绘制跟踪算法在成功率和精确率方面的对比图，如图4所示。本文算法与其他算法相比，在精确率与成功率方面取得了较为优异的成果。图4（a）中，本文算法精确率达到了0.855，高于其他算法；在图4（b）中，本文算法在成功率方面略低于ECO算法，但高于其他基于手工特征的跟踪算法。

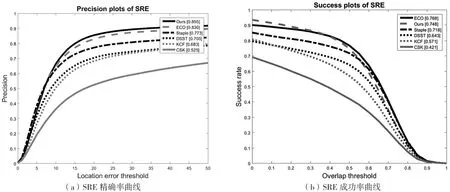
图4 跟踪测试基准的成功率和精确率曲线

表2可以更直观地看出本文算法在跟踪效果上的提升，然而引入卷积提取目标特征会耗费大量计算资源，造成速度下降，因此本文算法在速度方面低于其他基于手工特征的算法，但高于ECO算法。

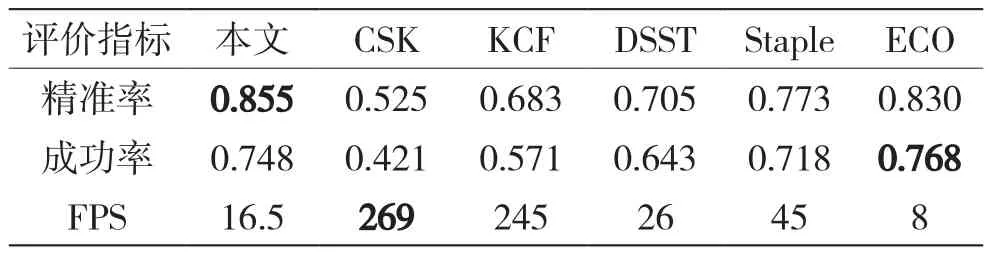
表2 不同算法的性能对比

由表3的实验结果可知，在面临11种不同情形的挑战时，本文算法的成功率均为最优值或次优值，尤其在背景混乱（Background Clutters，BC）、运动模糊（Motion Blur，MB）、平面内旋转（In-Plane Rotation，IPR）、低分辨率（Low Resolution，LR）、平面外旋转（Out-of-Plane Rotation，OPR）这几种情况下，算法成功率要优于目前最流行的ECO算法，证明了使用3层卷积层提取目标特征能够进一步增强跟踪算法的鲁棒性。

一方面，严格把关学业指导专业老师，能够保证学业指导专业教师队伍质量，另一方面，加强评价体系和考核制度，也能够增强学业指导专业教师的责任心和使命感。同时有利于及时发现学业指导过程中存在的问题，并有针对性的提出合理的对策和建议。从而有效促进提高教育质量和人才培养质量。

表3 不同挑战下算法的跟踪成功率比较

3.3 定性分析

图5给出了本文算法与3种具有代表性的算法DSST、Staple、ECO在视频序列上的跟踪结果。在图5（a）的ironman序列中，第35帧存在光照变化，第51帧发生运动模糊，本文算法提取的卷积特征能够很好地适应目标外观变化，鲁棒性更强，可以正确跟踪目标，而其他算法发生漂移。在图5（b）的soccer序列中，第112帧和145帧均存在不同程度的背景杂乱问题，本文算法和DSST算法可以正确跟踪目标。在图5（c）的motoRolling序列中，目标发生快速运动和运动模糊，只有本文算法能够正确完成跟踪，其他算法均产生漂移。在图5（d）的jogging序列中，第71帧中目标产生完全遮挡，第87帧目标重新出现时，只有本文算法和ECO算法能够继续跟踪目标，其余两种算法学习到错误信息造成跟踪漂移。

图5 本文算法与其他算法在部分视频序列上的跟踪结果

4 结 语

本文提出一种融合多层卷积特征的相关滤波目标跟踪算法，通过训练好的VGG-NET网络提取目标的多层卷积特征，浅层特征用于目标精确定位，深层特征用于增强目标的鲁棒性表达，从而代替对目标描述能力较差的传统手工特征，并通过对卷积特征进行筛选，降低特征维度，减少计算量，提高算法的跟踪速度。通过与几种主流相关滤波算法进行对比，证明了本文使用的多层卷积特征能够显著提高跟踪效果，尤其在背景混乱、运动模糊以及旋转等几种具有挑战性的跟踪场景下，具备更强的鲁棒性，达到了改进目的。