小学数学概念教学策略研究

江苏无锡市东北塘实验小学 周建东

数学概念就是客观现实中的数量关系和空间形式的本质属性在人脑中的反映，表现为数学语言中的名词、术语、符号等的准确含义。学习数学的过程就是一个不断运用数学概念进行比较、分析、综合、概括、判断、推理的思维过程。如何顺应学生的已有认知经验和学习发展状态，有效实施适合的概念教学，让数学概念入脑入心？笔者认为，要灵活运用和准确把握以下教学策略：

一、入境设“疑”

在教学中，教师要根据数学概念内容和学生的年龄特征，创设适合的教学情境自然引入概念，在学生入情入境中巧妙布障设疑。学生留“境”其中、因“疑”促学，兴致盎然、思维迸发，教学也就顺“疑”而为。

例如，在教学认识百分数时，笔者结合学校即将开展的排球联赛创设了如下情境：

1.出示表一

学校又要组织六年级排球联赛了，班主任想选一名发球手。

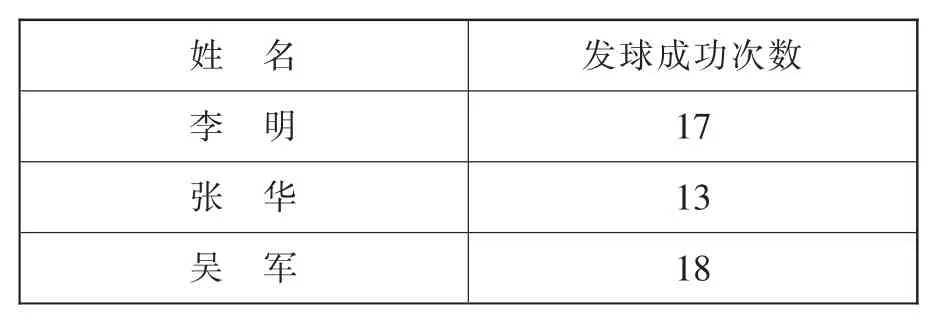
表一

设疑一：我们还需知道什么数据就能作出比较，选出发球手了？

2.出示表二

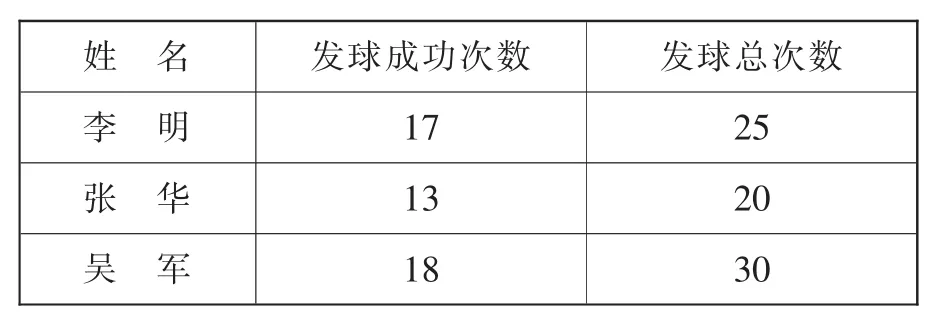
表二

设疑二：看了这两列数据，你打算怎样来比较呢？

学生疑惑顿生，单纯看发球成功次数或失败次数显然都不合理。笔者及时点拨：“我们能否换个角度，用学过的分数知识，可以怎么比呢?”

3.出示表三

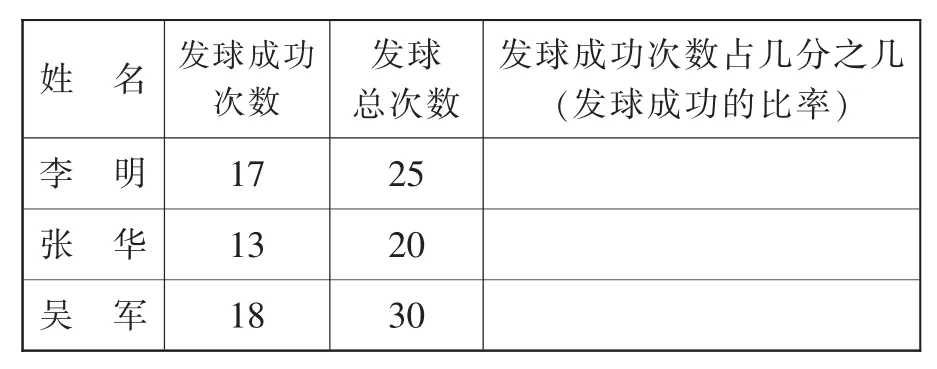
表三

至此，教师揭示概念：像上面这样表示发球成功次数是发球总次数的一百分之几的数，就称为百分数，这节课我们就来认识百分数。

在上述教学中，笔者在由表及里的情境中多次设疑，步步深入，学生的思维在不断的认知冲突中由困惑走向明朗，由表层触及本质。

二、默转潜“移”

有效的概念教学要把教学内容与学生已有的知识经验联系起来，根据学生已有的经验，唤醒和提炼学生已有的经验，并引导学生引申、推导出新概念，帮助学生建立概念。

例如，在教学比的基本性质时，笔者首先让学生说说150÷60简算方法，得出等式150÷60=15÷6=2.5。“你能根据比与除法、分数之间的联系把这个除法等式分别改写成分数、比的等式吗？”，150∶60=15∶6=5∶2。 “除法简算、分数化简的依据分别是什么？”笔者追问，“由商不变的规律、分数的基本性质，观察比的等式，猜猜比有什么性质？”学生猜想：比的前项和后项同时乘或除以相同的数，大小不变。笔者于是出示例题，让学生把比值相等的比写成一个等式4∶5=16∶20=40∶50，引导学生按照一定的顺序观察，从中发现了什么？接着又让学生自己写出一些比值相等的比组成的等式，验证是否适用。“这样的等式写得完吗？”“对于刚才发现的结论，你有什么需要补充的？”至此，比的基本性质也就瓜落蒂熟了。

在上述教学中，笔者由比与分数、除法之间的联系，从写出的等式中，助推学生联系已学的商不变的规律、分数的基本性质，通过猜想、验证、归纳得出了比的基本性质，新知在旧知的土壤中激活、生长，默转潜“移”。

三、集思广“议”

学生学习概念要经历一个复杂的认知过程，才能实现从感性向理性过渡。教师除了要提供典型、丰富的实例，让学生感知、比较，还要引导学生进行多层次的辨析，层层深入，使概念的一些隐性的本质属性凸显出来，使概念更加清晰、明确，使学生对概念内涵的理解从文字层面进入实质层面。也就是说，数学概念的学习需要让学生经历充裕的思考和互动交流的过程，从而由困惑走向顿悟，由表层走向深入。

例如，笔者在教学认识负数时，先让学生从一些数中挑出负数和正数，并说说自己是怎么挑出来的，接着让学生以挑出的“-2”为例，结合自己生活中看到的例子，用自己喜欢的方式在纸上表示它的含义。学生思维顿开，通过画图、列式、写话等形式表达着自己的理解：画图表示出电梯-2楼来区分地下和地上；游戏得分为-2分来区分输和赢；商店营业额-2万元来区分亏损和盈利；温度计上-2℃来区分零下和零上温度……笔者接着设问：“这些负数和正数是以什么来区分的？”“每组中的两个词有什么关系？”“黑板上这些数你能按从小到大的顺序排列出来吗？”“0应该放在哪里？它是什么？它和负数正数之间有着怎样的关系？”“现在你能用一句话来说说对负数和正数的理解吗？”学生思得周全、议得热烈。

在上述教学中，笔者基于学生的认知放手让学生去思考，才会涌现出众多丰富而又真实地想法，它是有根基、接地气的；巧妙设问推一推、引一引，舍得花时间让学生互动交流，思维的火花才会在激烈的碰撞中显现。

四、探究诠“译”

在概念获得的过程中，学生不是被动、消极地等待各种刺激的出现形成联结，而是积极、主动地去探究这一概念。概念教学应当鼓励学生自己去探索，主动建构和理解。

例如，笔者在教学多边形的内角和时，先让学生求出一个四边形内角和是多少，在随后的交流中引出了用分割法得出内角和比较方便。“是不是任意一个四边形的内角和都是360°呢？你能自己画出一个四边形研究它的内角和吗？”学生用分割法在自己所画的四边形中进行了验证。此时，笔者又提出要求：“五边形、六边形的内角和又分别是多少呢？”在随后的展示交流中适时追问怎样分、怎样算？学生从中体会到：要从某一顶点出发有序连接不相邻的顶点，就把一个多边形分割成了若干个三角形，若干个三角形的和也就是多边形的内角和。于是笔者出示导学单（见表四），让学生大胆探索其他多边形的内角和。

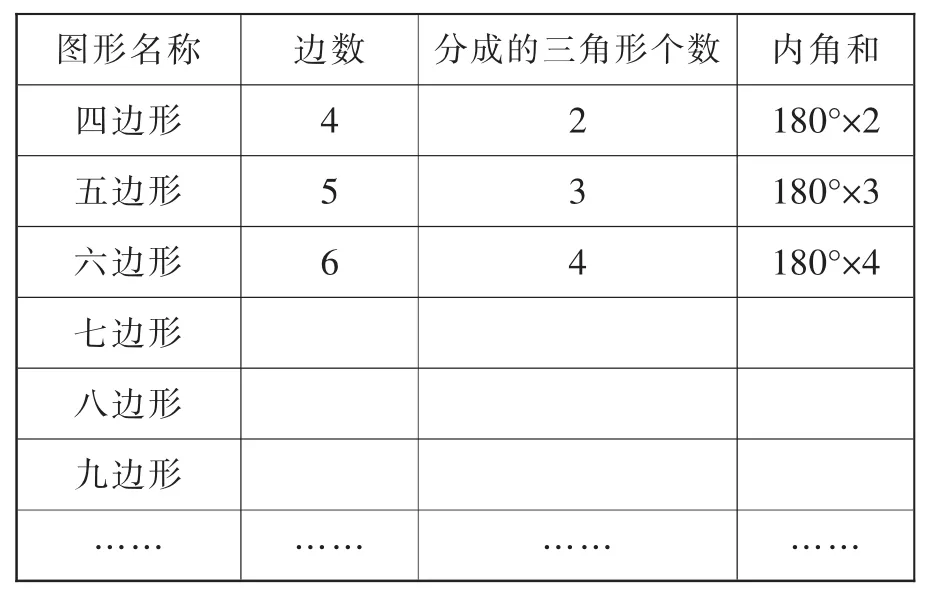
表四

当学生通过探究填表后，让学生观察表中数据，你有什么发现？学生很快找到了其中的规律。

在上述教学中，笔者通过四边形内角和的探索引出了分割法，通过五边形、六边形内角和的探索强化了有序分割，多边形的内角和就是转化成若干个三角形内角和的关键点。随后通过其他多边形的深入探究，最终顺利得出了多边形内角和的规律。

五、如虎添“翼”

在经历了概念的发生和形成后，还要让学生对概念有更深刻的体验和理解，使学生能将学到的数学概念融入问题解决中，这样才能够让这些数学概念在课堂上变得生动鲜活起来。

例如，在认识“公顷”后，笔者让学生课后手拉手围成一个边长10米的正方形，感受1公顷有多少个这样的正方形，以小组为单位去调查学校操场、餐厅、篮球场的数据，算一算1公顷分别有多少个这样的场所，调查学校的占地面积大约有几公顷，自己居住的小区的占地面积大约有几公顷……又如在学习了“比例尺”的知识后，让学生去调查统计学校各幢建筑的形状及数据，绘制一份手绘地图，向新同学或家长介绍自己美丽的校园。再如在进行“认识角”的练习时，紧紧围绕角是由一个顶点和两条直直的边组成这一本质，设计了辨析题、判断题，在变换的图形中找角、动手折角、数角这些变式题，进一步巩固了学生对角的概念的认识与理解。当学生深刻领悟概念之后，解决实际问题也就如虎添翼，迎刃而解，在实际问题的解决过程中，又加深了对数学概念更好的理解与记忆。

总之，我们要基于学生的身心特点认真研读教材，准确掌握数学概念内容，通过各种恰当途径，灵活运用各种策略，为实现既定的概念教学目标而努力。