在延迟支付条件下基于EOQ模型的库存选址模型研究
2019-12-10薄录娟徐伟
薄录娟 徐伟

摘要:合理的设施选址与其他层次决策(库存策略或运输策略)的结合,可以降低物流成本和资源浪费。从企业全局的角度出发,制定基于延迟支付条件下的最佳订货周期方案,然后综合考虑设施选址和运输成本,完善库存成本与运输成本的衔接关系,设计出最优的配送中心选址模型。文章在国内外关于物流配送中心选址研究的基础上,系统地研究了延期支付期限的EOO订货模型对库存成本的影响,再结合运输成本,实现选址成本的最优化。
关键词:供应链金融;延迟支付;EOQ模型;库存选址
中图分类号:F253 文献标识码:A
0引言
配送中心是将供需结合起来,影响物流网络的运行和经济效益的重要环节。工厂的战略选址和战略库存控制是影响物流系统优化的两个关键问题,综合研究这两个方面,可以有效地避免局部优化,合理解决单方面考虑库存位置或控制存在的问题,有助于提高物流运营的整体效率,降低物流成本。因此综合考虑建设成本、运输成本、库存成本与设施选址之间的相关关系是物流系统规划发展的关键。
大量的研究表明,基于延迟支付的经济订货批量模型的研究有很多,但是基于延迟支付分析的最优订货策略的研究很少。陈丹丹等建立了基于库存策略的选址决策模型并对其进行优化,确定所需要建立的配送中心的数量和位置,以及所选配送中心的客户分配和库存决策;王静通过将库存决策与运输成本相结合,建立了配送中心选址模型并对其进行优化研究;税文兵翻通过将库存成本考虑到配送中心的动态选址模型中,充分地将库存成本考虑到设施选址中,改良了算法。
本文研究了配送中心整体的库存策略和位置分布,考虑到客户需求是随机的,是服从正态分布的,订单具有提前期,配送中心具有存储容量约束,为了达到一定的客户服务水平,降低货物的安全库存,选择了延期付款的最优订货策略;为了最大限度地降低配送中心的整体成本,考虑到最佳成本,使配送中心的位置问题更符合产品多样化的实际需求,提出了基于延期付款的最优库存策略与配送中心选址联系起来的决策优化模型。
最后,在研究的基础上,考虑到配送中心的数量和位置以及所选配送中心的随从策略,而配送中心是由客户决定,地点的总成本也是由客户决定。基于以上研究目标,提出了问题的基本假设,并通过分析和推导,建立数学模型,并对其进行求解。
1基于延迟支付期限的EOQ模型的构建
配送中心位置的确定,决定了整个物流网络和其他层次的结构,也是确定设施数量、客户位置和分配计划的重要依据。就单个公司而言,物流网络的合理化是其他层次规划的前提,也会影响选址的决策。因此,在确定配送中心时,优化存储成本是非常重要的,在由供应商、零售商和客户组成的三阶段供应链中,供应商允许零售商延迟付款,零售商也为客户提供延期付款的优惠条件,鼓励买家购买他们的商品,从而增加了交易成本和销售量。而延迟支付可以使得经济订货批量模型中库存成本的最优化,因此注重延迟支付的库存决策尤为重要。
1.1模型的基本假设
(1)零售商的订货量有充分的延迟支付时间,即Q≥Qδ,所有的支付必须在t=M时支付;
(2)只考虑供应商、零售商和消费者的三相串行结构;
(3)年需求是随机的,不允许缺货;
(4)供应商提供给零售商固定的延迟付款期限。在延迟支付期间,零售商销售的资金会获得一定的利息收入L,到货期后,零售商会支付货款并支付一定数额的费用,零售商还需要支付一定的占据资金的利息,假定这部分资金是零售商的,银行和其他机构的贷款利率为Ik。
(5)符号说明:D:商品的年需求量;C:单位产品的采购成本;r:订货周期;M:供应商提供给零售商的延期支付期限;A:发生一次订货所需的固定订货费用;Q:零售商每周期的订购批量;h:单位产品单位时间库存保管费用;Ie:单位库存年收入利息;Ik:单位库存年支出利息:Ik>Ie;TC:零售商的年总费用。
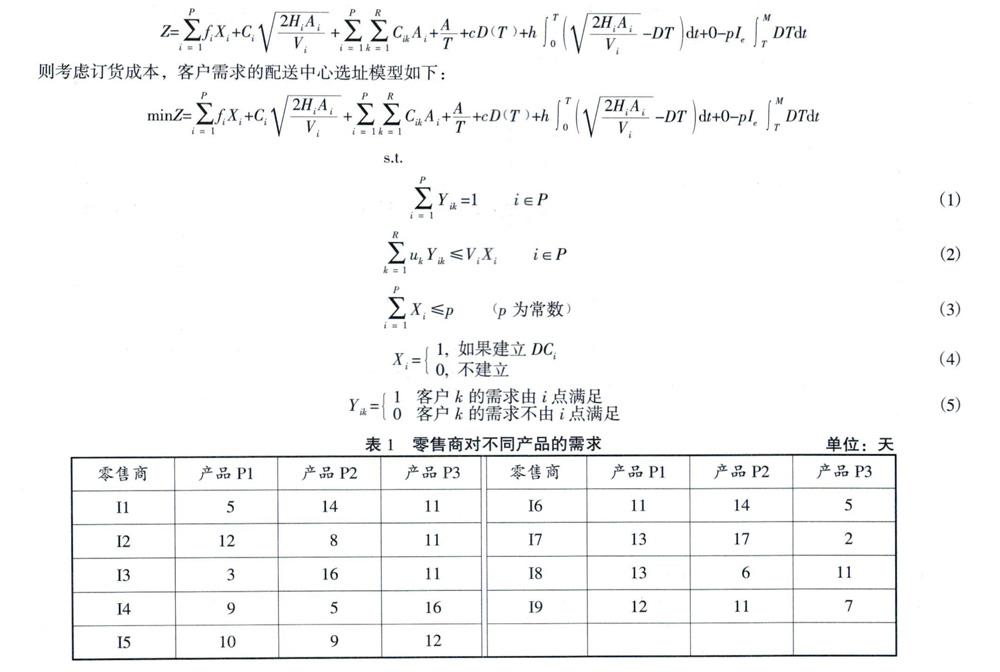
1.2模型构建
随着需求量的增加,基于延迟支付条件下,订货频率会发生变化,而零售商的库存会逐渐减少,库存水平随着时间的变化可以满足:
约束式(1)表示的是一个客户的需求只能被一个配送中心满足,即客户的需求不能被分割;
约束式(2)表示的是配送中心一旦被修好,它所满足的客户需求量不得超过它本身的储存能力;
约束式(3)对配送中心的数目进行了规定;
约束式(4)0-1变量约束,表示是否选为配送中心;
约束式(5)0-1变量约束,表示客户的需求是否被配送中心i满足。
3实例分析
基于以上最终的最优模型,提出了一种改进的多目标粒子群优化算法(MPso)对其求解。粒子群优化(PSO)的基本思想是寻找食物时,随机模拟鸟类的捕食行为,发现在鸟群中食物最丰富的地方。每只鸟的位置/路径是独立变量的组合,并且在到达的每个点的密度的食物是一个函数值。每个搜索将根据自身的经验(为自己的历史搜索的最佳位置)和人口交换(人口历史搜索的最佳位置)调整其搜索方向和速度。这就是所谓的跟踪极值找到最佳的解决方案,而敏感性分析是对影响配送系统总成本的主要参数。
3.1粒子群算法的优化过程
(1)参数的初始化,设置算法运算的初始参数;
(2)外部归档集初始化;
(3)计算外部归档集中各粒子的拥挤距离;
(4)选取全局的最优解;
(5)粒子速度与位置更新;
(6)计算种群适应度值,更新Steml信息矩阵。
某企業嚅要构建由工厂、配送中心和零售商组成的多产品分销网络。假设候选的配送中心数有3个,零售商有9个,有3种产品,配送中心存在仓储空间和库存资金两种资源限制。由于数据可得的局限性。数据由参考文献中随机生成。零售商每天的需求如表1所示;配送中心的单位库存持有成本和固定建设成本分别如表2、表3所示;从工厂到配送中心的单位运输成本和两种资源总量如表4、表5所示;不同产品对资源的单位消耗水平如表6所示;规划期限为300天。
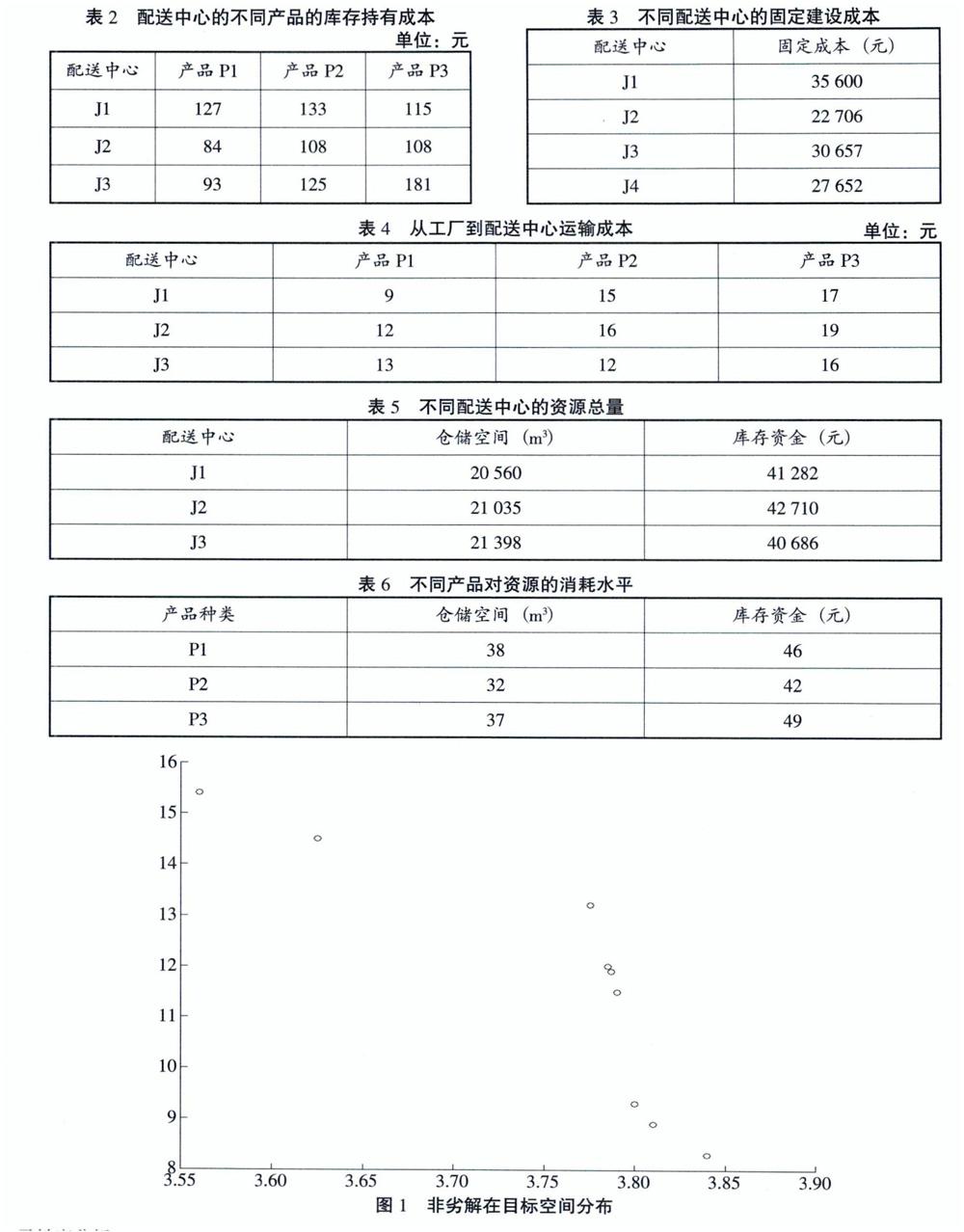
结合以上实例,粒子群算法参数设置为:粒子群个数N=50,迭代次数为ger为200,惯性权重为0.8,自我学习因子为c1=2,群体自我学习因子为c2=2,通过MATLAB编程,得出的非劣解在目标空间中的分布如图1所示:
3.2灵敏度分析
此混合整数非线性规划模型由LINGO软件解决,灵敏度分析是用于研究原始数据不准确或发生变化时最优解的稳定性。以上述实例数据为基本数据,对相应的参数进行取值并对其进行上下浮动取值,如从工厂到配送中心的运输成本取值为20,上下浮动10%,即减少10%(取18)和增加10%(取22),对比模型求解结果和基本数据求解结果的差异,从而得到所建模型的灵敏度。
结果如表7所示,各参数都存在一个变动区间,当这些参数在变动区间内变化时,选址(X变量)和分配(Y变量)结果不发生改变;而订货批量(Q变量)除不随配送中心固定成本的变化而变化外,其它都要发生变化。从表中可以看出,库存持有成本稳定性相对最好,变化区间跨度超过200%;其次是零售商需求和单位运输成本,变化区间超过50%。
4结论
本文在独立订货策略的框架下研究了商品库存问题,为了使选址成本、库存成本和运输成本之和最小化,建立了混合非线性规划模型。设计了一个求解模型的实例,并通过实例验证了模型的有效性。最后通过灵敏度分析表明,模型的选址和分配变量对各参数的变化都表现出一定的稳定性。
将运输问题、选址决策、库存决策、运输决策和时间融合在一起的研究涉及物流业的许多方面,如物流设施选址,物流网络设计,配送网络设计等,它们的应用也会越来越多。因此,企业或专业的物流企业合理选择物流配送中心的位置是非常重要的。因此,物流配送中心的选址有继续研究的前景。随着研究的深入,也会加入更多的因素,为企业决策者提供更好的决策依据。由此得出,根据成本进行分析研究,建立最优的配送中心模型是当前的发展优势。
