奇思·方法·学习

任卫兵

【教学内容】

帕斯卡与“三角形内角和”的故事

1.故事导入

帕斯卡（1623—1662）对概率研究做出了很大贡献。他是法国著名的数学家、物理学家、哲学家和散文家。

帕斯卡的父亲是一位受人尊敬的数学家，有一天帕斯卡问父亲，什么是几何？父亲很简单地回答说：“几何就是教人在画图时能作出正确又美观的图。”于是帕斯卡就拿了粉笔在地上画起各种图形来。画着画着，12岁的帕斯卡发现任何一个三角形内角和都是180°。

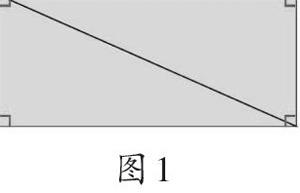
问题一：你知道帕斯卡是怎样通过长方形的内角和推想出其中一个直角三角形的内角和的吗？

长方形的四个角都是直角，长方形的四个角的和一定是360°。把长方形沿对角线一分为二，就变成两个直角三角形，每个直角三角形的内角和就是360°除以2等于180°。因为任意一个直角三角形都可以看作是长方形剪开的，所以任意直角三角形的内角和一定是180°（如图1）。

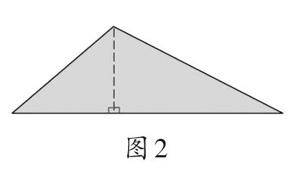
问题二：你知道帕斯卡是怎样通过直角三角形的内角和推想出其他三角形的内角和的吗？

任何一个钝角三角形都可以沿高分为两个直角三角形，两个直角三角形的内角和180°+180°=360°，而其中有两个直角拼在一起成了一条直线，所以真正作为钝角三角形的三个内角的和就是360°-90°-90°=180°。同样的道理可以说明锐角三角形的内角和也是180°（如图2）。

2.故事启迪

思路点睛：求多边形的内角和，就是看这个多边形最少可以分成几个三角形，分成了几个三角形，多边形的内角和就是180°乘几。

3.故事延伸

古埃及人从铺地板中发现，三角形三内角和为一平角（即180°）。在图3中，绕一顶点的六个角，合起来一共是一周角（即360°），因此正三角形三内角和为一平角。这虽只是特例，但却是进一步发现真理的契机。

利用旋转铅笔的实验，也可得出三角形三内角和为一平角的结论（如图4）。

【课堂实录】

一、用故事丰富学生思想

师：回忆一下，我们是怎样研究三角形的内角和的？

生：我们是用量、拼、折等方法，来验证三角形的内角和是180°的。

师：300多年前，有一个名叫帕斯卡的法国男孩独自发现了任何一个三角形的内角和都是两直角。

课件播放帕斯卡发现“三角形内角和”的故事。

教师出示问题1和问题2，请学生先独立思考，再在小组内交流，最后进行全班汇报。

生：因为任何两个完全一样的直角三角形都可以拼成一个长方形，长方形的内角和是360°（4个直角），每个直角三角形的内角和就是180°（2个直角）。

生：两个直角三角形中所有锐角的和是180°（2个直角），那么一个直角三角形中两个锐角的和就是90°（一个直角），再加上一个直角，所以直角三角形的内角和是两个直角，即180°。

生：钝角三角形可分成两个直角三角形，两个直角三角形的内角和是360°（180°×2），其中两个直角正好拼成一个平角，所以钝角三角形的内角和是360°-180°=180°。

生：不管是钝角三角形还是锐角三角形，都可以分成两个直角三角形。因为每个直角三角形的两个锐角的和都是一个直角，而钝角三角形或锐角三角形的内角和包括两个直角三角形的所有锐角，所以无论是哪种三角形的内角和都是两个直角，也就是180°。

师：为什么要把两个直角三角形拼成长方形，要把钝角（或锐角）三角形分成两个直角三角形呢？

生：这是把未知的知识转化成已经知道的知识。

师：把未知转化成已知，是一种很重要的数学思想。

师：把任意三角形分成两个直角三角形，两个直角三角形是6个角，而任意三角形是3个角。这6个角和3个角一样吗？

生：从图中就可以看得很清楚，这6个角中有2个角拼成了大三角形的1个角，还有2个直角拼成了1个平角。

生：也就是说，6个角中有2个直角与大三角形的内角没有关系，剩下的4个角就等于大三角形的3个内角。

师：这下我们不仅看清楚，也真正听清楚、理清楚了。

二、分图形实现多元表征

师：拿出一张五边形的纸片，自己想想办法，求出它的内角和，再在小组内交流。（学生独立探索后小组交流）

生：我把五边形分成了3个三角形，3个三角形的内角和相加就是五边形的内角和，是180°×3=540°。

生：我把五边形分成了4个三角形，其中有4个角拼成了一个平角，五边形的内角和是180°×4-180°=540°。

生：我从中间选一点，把五边形分成了5个三角形，有5个角拼成了一个周角，五边形的内角和是180°×5-360°=540°。

师：听了刚才几位同学的介绍，大家还有什么问题吗？

生：为什么把五边形分成的三角形的个数不同，最后算出的内角和还是不变的？

师：好深刻的一个問题啊！同桌两人讨论讨论。

生：把五边形分成3个三角形大家都明白。分成4个三角形，因为有4个角拼成的一个180°的角在一条边上，不包含在五边形的内角和中，所以五边形的内角和等于4个三角形的内角和减去一个180°的角，也就是3个三角形的内角和。

生：我来解释一下，把五边形分成5个三角形，因为中间5个角拼成的一个360°的角也不包含在五边形的内角和中，所以五边形的内角和等于5个三角形的内角和减去一个360°的角，还是等于3个三角形的内角和。

师：谁还有不一样的想法？

生：我们可以用乘法分配律来说明。分成4个三角形，五边形的内角和=180°×4-180°=180°×（4-1）=180°×3……

师：我要打断你一下，用这样的方法，分成5个三角形，五边形的内角和——（根据学生回答，完成板书：五边形的内角和=180°×5-360°=180°×5-180°×2=180°×（5-2）=180°×3。）

师：看来，要求多边形的内角和，“分”是一种好办法。把五边形分成三角形，最少分几个？怎么分？

生：最少分3个。只要从一个顶点出发，另外连两条线，就可以分成3个三角形了。

师：如果是六边形、十边形、一百边形呢？

生：六边形最少可以分成4个三角形，十边形最少可以分成8个三角形。

生：一百边形最少可以分成98个三角形。

师：把多边形分成三角形的个数究竟和什么有关呢？这其中有什么规律？

生：分成的三角形的个数和连线条数有关。

生：我认为和边的条数有关。

生：我觉得和多边形的顶点个数有关。

师：其实大家的想法都很有道理。从一个顶点出发，连线的数量总比三角形的个数少1。另外，多边形边的数量和顶点的个数也是相同的，它们与连线数的差也是不变的。这其中的规律，就留给大家今后去揭示吧……

三、借实验感悟数学原理

师：关于三角形的内角和，有人曾做过这样一个实验（课件播放实验视频，见图4）。

师：请大家在纸上任意画一个三角形，根据刚才的实验步骤，动手做一做。

生：我发现以三个顶点为中心，按顺时针方向旋转，最后铅笔正好换了一个方向。

生：按逆时针方向也可以。

师：关于“三角形的内角和”，还有哪些不同的推理方法呢？到时候把你的故事和大家一起来分享吧！

【教学思考】

一、好的故事具有更新、丰富认知系统的功能

关于“三角形的内角和”，现有教材多采用量、拼或折的方法，尽管这些方法比较适合学生的年龄特点，但思维含量不高。上述案例中以“帕斯卡与三角形内角和” 的故事引入，一下激起学生的探究欲望。通过方法引领、自主推想、质疑问难、补充完善，学生的数学思考、理性思维得到了“恣意”的生长。同时，透过故事，还能从中感悟到“转化”的数学思想。学生发现，无论是三角形内角和的规律，还是平面图形的面积推导，它们都是建立在“转化”这一数学思想基础上的，而这种数学思想统领下的知识建构，是一种高观点下的知识建构。

二、好的教学一定是多元的、发散的

受帕斯卡与三角形内角和故事的启发，在独立探究五边形内角和的问题时，学生自然会尝试、迁移这一数学思想方法。在把五边形分成三角形时，由于给足了学生探究的空间，学生得以尽情地去思考、去研究、去表达。其中有从一个顶点出发来分的，有从边上一点出发来分的，也有从图形中间一点出发来分的。多元的方法，拓宽了学生的思路，发散了学生的思维，激活了学生强烈的问题意识——“为什么把五边形分成的三角形的个数不同，最后算出的内角和还是不变的？”“把多边形分成三角形的个数究竟和什么有关呢？”学生努力调用已有的知识、经验，用独具个性的表达诠释自己的理解与思考。这样的学习体验是深刻的、弥足珍贵的，浸润于这样的数学学习环境中，学生的思考力、表达力、创造力必然会潜滋暗长。

三、好的学习需要找到一种“似曾相识”的感觉

课中，教师借助旋转铅笔的实验，让学生感悟數学的“简约”与“神奇”，并使这一数学“意象”固着在学生的头脑中。随着学生已有知识、经验的增多，借助某一契机，他们会猛然发现原先的“旋转铅笔”的实验与“过三角形一顶点作对边平行线”的方法有着一种内在的、本质的联系。先前固着在学生头脑中的已有“意象”与新的“对象”发生了粘连，进而产生了新的联结。这样的一种“似曾相识”的感觉恰是数学的迷人之处。

（江苏省南通市通州区教师发展中心   226300）