树木生长方程的融合分析研究

孙杰，孙小珺，尹若波,张德全,王克华,于凌飞，张靖

(1.龙口市国有林场,山东 烟台 265701;2.山东省龙口市森林病虫害防治站,山东 烟台 265701;3.山东省林业外资与工程项目管理站,山东 济南 250014；4.山东省林业监测规划院,山东 济南 250014)

为了全面提升森林质量，迅速扭转种质资源趋于退化的不良态势，从2010年开始，数学经验方程在林业研究方面得到了广泛应用，胡海燕[1]、王亲波[2]等对树木成熟龄进行了系统研究；巩延苹[3]对树木生长量与降水量的关系进行了研究；张德全[4]对气候干湿周期进行了研究；矫兴杰[5]、张靖[6]、董兴囤[7]、杨科家[8]分别在碳储量、生长节律、光照影响与生长因素影响剔除等方面进行了研究。笔者经过长期研究发现，光照、降水、气温是影响树木生长的主要生态因子，但是其影响程度需要在时间尺度上进行表达。笔者认为时间因素也应是影响树木生长的因子，只不过这一因子具有周期性、恒定性、均衡性、不可改变等特点，别的因子表现均为通过时间因子尺度上的表达，笔者经过研究发现，树木的生长方程y=exp(a+bx)(其中y为树木的各种生长量指标，如树径、树高、材积等，为因变量；x为影响因变量变化的各项影响因子值，即时间、光照、气温、降水等；a，b为待求系数。由于本函数为成长函数，树木一般不会出现负增长，故b一般为正值，下同)和阻力方程y=exp(a-b/x)(方程中的符号含义同上一经验方程)，通过一定系数的换算，加以融合，只要样本数一致，起始年龄一致，不论龄阶(两个年龄相近样本间隔的时间长度)的大小，其试验精度是一致的，笔者以一棵300年生的侧柏解析木进行研究。

1 资料来源

解析木材料为2013年12月采自山东省枣庄市山亭区山亭林场，是所有试验解析木中树龄最大的一棵。

2 研究方法

笔者曾用经验方程对树木生长过程作过多次研究，用经验方程y=exp(a+bx)(其中y为树木的各种生长量指标，如树径、树高、材积等，为因变量，x为影响因变量变化的各项影响因子值，即时间、光照、气温、降水等，a，b为待求系数，由于本函数为成长函数，树木一般不会出现负增长，故b一般为正值)研究树木生长快慢，及各项因子及其交互作用的影响程度，用经验方程y=exp(a-b/x)(方程中的符号含义同上一经验方程)来研究因变量的平均变化速度和即时变化速度，即x=b时，因变量平均变化速度最快，当x=b/2时即时变化速度最快(通过对方程的一阶求导和二阶求导可得)，用以追求效益最大化。笔者经过多年大量研究发现，如果将这两个方程加以融合，不分树种、立地条件的差异，只要是起始年龄相同、时间因素对应的样本间隔一致或者是具有相同的倍数，再加上适当的系数调整，其实验精度能够达到完全一致。

先用经验方程y1=exp(a1+b1t)和y2=exp(a2-b2/t)(为了区别其间，在函数和待求系数加了下标)建立树木生长量与树木生长年龄的回归关系，求得待求系数a1、b1、a2、b2，在这里y1、y2为以时间t为自变量、树木实际生长量(实测值)为因变量而到的经验方程拟合值。

如果令y3=exp(a3+b3t)和y4=exp(a4-b4/t)，y3、y4为对y1、y2而言， 将上述的树木生长量(实测值)替换为y1^m×y2^n，其中m、n为小于的纯小数，满足m+n=1的条件，并且使得方程y3、y4的方程拟合精度完全相等，m、n用电子表格计算采用逐步接近的办法解决求算问题，笔者将求算精度定为10亿分之一，即1E-9。经过大量验算得出以下结论：不分树种、立地条件的差异，不分树木生长指标性质的不同(如树径、树高、材积等)只要是起始年龄相同、时间因素对应的样本间隔一致或者是具有相同的倍数，再加上适当的系数调整，y3、y4的方程拟合精度完全相等，笔者把一精度定义为平衡精度。

3 研究过程

3.1 生长过程原始拟合

笔者以300年生样木为例，对这一科学研究方法进行论述。先用解析木资料建立树木生长量与树木年龄的经验方程。用D2-0代表地径项目，用D2-0.5代表0.5 m高处树径项目，余者类推，用H2代表树高项目，用V2代表树木材积项目。用Y(t)代表以时间(树木年龄)为自变量，以树木各种指标的生长量为因变量的函数。分别利用经验方程y(t)=exp(a+bt) 和y(t)=exp(a-b/t)建立数字回归方程。用电子表格计算，得到试验结果如表1、表2所示。所有项目均通过R检验、F检验和t检验，拟合精度均达到99.39%以上，最高的达到99.98%。表中的翻番时间，为该树木生长量每增长一倍所需时间，用来形象地表达树木生长速度。从表1看出，树木7.0 m径增长速度最快。表2中的tm、tz分别为函数y(t)=exp(a-b/t)的一阶和二阶导数值，前者是在此时刻树木生长指标平均增长速度最大，后者是即时增长速度最大，前者是后者的二倍。试验精度之高，说明笔者选用方法及试验数据准确，为此笔者不再做类似的适合性检验。从表2可以看出，树高6.5 m以上的侧柏寿命可达3 700 a以上，树高7.0 m以上的侧柏寿命可达10 665 a,中国曾有古柏寿命5 000 a以上的传说和记载，至于1万年以上只能是笔者研究的期望寿命，随着对古树名木保护力度的加大，笔者因为寿命万年的古柏，将会不再是传说，而成为现实。

表1 300年生侧柏生长过程经验方程拟合表(1 a龄阶、成长方程)

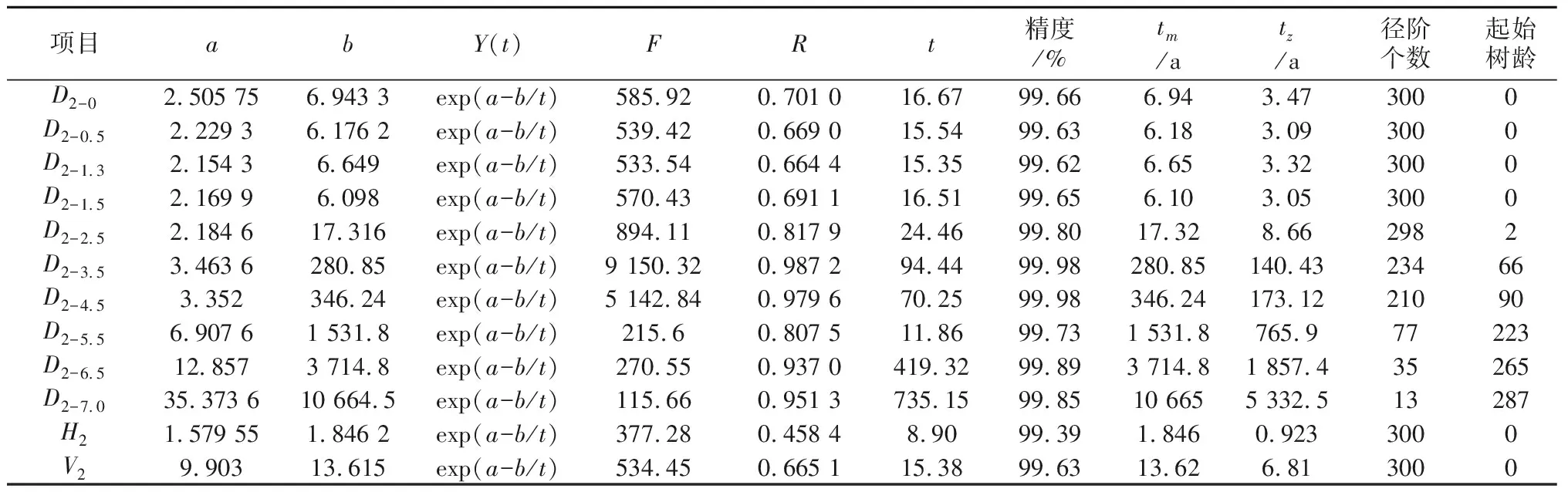
表2 300年生侧柏生长过程经验方程拟合表(1a龄级、阻力方程)

3.2 生长过程经验方程融合

将表1、表2中的方程拟合值分别乘以一个适当的调节系数m与n(前面已作过论述)，然后将二者的乘积作为因变量的取值，把时间当作自变量，分别以y(t)=exp(a+bt)和y(t)=exp(a-b/t)建立经验方程进行分析，计算结果如表3与表4所示。表3中的相对贡献率的计算以D2-0项目为例进行说明，它的相对贡献率=1/〔1+(166.49-102.94)/102.94〕×100%=61.83%，式中116.49、102.94分别为表3、表1中的树木该生长量指标，这就是说若要达到这一均衡状态，得采取措施使树木生长势能降低1-61.83%=38.17%，这只是理论上的假设，我们没有必要去做样的事情，只是为了大家更好地理解这一问题，笔者采用了相对贡献率的概念(下同)。由表3可以看出，起始与终止年龄一致，在同一龄阶条件下，方程的相关系数和拟合精度均相等，随着起始年龄的增大，其精度和相关系数逐步增大，起始年龄达到287 a的D2-7.0项目，其拟合精度达到99.999 9%，几乎接近100%，相关系数也非常接近于1，随着年起始年龄的升高，调节系数m逐步接近0.5的水平，说明树龄越高，生长的阻力作用明显上升，表现树木生长势的衰弱.调整系数m以树高为最低，这是由于所有植物都有趋光性，为了争得阳光的普照，树木向高处发展的内在动力是很大的，笔者认为风的作用是影响树高生长的重要因素，风抑制了树高生长速度，树木的内在生理机制就要产生抵制这一抑制作用的动力。表4的研究精度及关于精度的各指标(如相关系数、F值等)，与表3是一致的(理论上是同一值)，但是各种高度的径生长量方程拟合结果，使得方程b值有所降低，说明随着平衡状态的达到，树木的生长的上升作用有所减弱，阻力作用有所升高，树木的预期寿命有所降低，但总体变化不大。

表3 300年生侧柏生长过程经验方程融合平衡状态表(1 a龄阶、成长方程)

表4 300年生侧柏生长过程经验方程融合平衡状态表(1a龄阶、阻力方程)

3.3 生长过程经验方程融合的平衡对比试验

将3.1.2节试验中的m、n值保持不变，将二者的积改为二者的商，按照笔者的研究结果，二者的商就是对一方的排除，因此笔者定义为相斥状态。重新做同样的方程拟合试验，试验结果见表5与6所示。从表5看出，样本越多，试验精度越高，样本数低于77，试验精度低于90%，笔者不再列出，样本数目为77时，试验精度为84.04%，样本数为36时，试验精度为85.69%，样本数为13时，试验精度为78.29%。阻力方程和上升方程的研究精度，样本数越多，越比较接近，越少则偏差越大。同表3、表4相比，试验精度有所降低，特别是样本数量较少的降低更为明显。由于对阻力作用的排除，而使阻力方程的b值为负值，失去了实际意义，表明阻力作用相对被排除。相对贡献率由平衡状态的平均值76.33%降为相斥状态的21.31%，相对下降比率为72.08%，这就是说相斥状态相对于平衡状态而言，阻力作用的被排除的同时，上升作用被排除72.08%。由于这一试验中，阻力方程的b值为负值，已失去实际意义，说明阻力作用已完全被剔除。如果将该实验的商，替换为商的倒数，即阻力方程的拟合值与上升方程拟合值的商(调整系数不变)，则成长方程与表6相比，a值、b值、相对贡献率只是符号不同(正负相反)，其余项目数据均保持不变(如精度)等，这样不仅上升作用被剔除，而且为负增长了，笔者不再列出阻力方程。从表6中可从看出，方程参数b值明显变小，这就是如果上升作用被剔除，树木的期望寿命明显降低，即树木的生长势(即生命力)明显削弱。这就是说这两者之间是完全相当的，为树木的上升作用和阻力作用的剔除提供了思路和方法。如果将二者的调整系数对调，将是调整后的实际状态。从中也可从看出，时间对树木生长的影响是一种乘数效应或者指数效应，而不是加法效应，笔者长期研究证明这一结论对于光、温、水等量化影响因子具有同样的效应。

表5 300年生侧柏生长过程经验方程相斥状态表(1a龄阶、成长方程)

表6 300年生侧柏生长过程经验方程相斥状态表(1a龄阶、阻力方程)

3.4 生长过程经验方程融合的现实状态试验

3.3节最后提到，将上升方程和阻力方程的调整系数对调，就是m和(1-m)对调，就是说调整系数上升方程的m次方相当于阻力方程的(1-m)次方，这就是说实际发挥的效应作用为上升方程的(1-m)次方，阻力方程的m次方，以二者的积为因变量(y),以时间t为自变量进行方程拟合试验，试验结果如表7、表8所示。由表7可以看出，同原始状态相比，试验精度有所提高，其中5.5 m径项目提高幅度最大，平均提高0.087%，5.5 m径项目提高0.129 8%。与原始状态相比，时间因素相对贡献率为82.62%，而平衡状态平均为78.02%，相对于平衡状态时间因素相对贡献率提高4.6%，因此相对于平衡状态和原始状态而言，表5的试验结果更能准确地反映时间因素对树木生长的影响的表达。原始状态时间因子的影响包括光、温、水的累积效应对树木生长的影响，而现实状态则是至少是部分排除了光、温、水的累积效应对树木生长的影响，至于能否完全排除，有待在以后的研究中逐步加以解决。由表3、表7可从看出，3.5 m径至7.0 m径项目时间因素相对贡献率均在100%以上，有的项目超过100%，是试验偏差所致，理论上应是100%，说明光、温、水的累加效应在树木尚未郁闭前，由于它们的作用不能100%地发挥出来，因此它们的累加效应是不能完全吻合的，树木完全郁闭后(郁闭度0.8以上)，光、温、水的累加效应完全发挥，与时间的作用完全相一致。总之，表7的试验结果，同表1、表3相比，更能准确无误地表达时间因子对树木生长的影响作用。表8同表4相比，各方面指标变化不大，试验精度有所提高，因此阻力方程的实际状态与平衡状态区别不大，可以互相取代。因此成长方程更能准确反映树木生长实际情况，树木的成长动力远远大于其阻力作用，树木得以生存和成长。

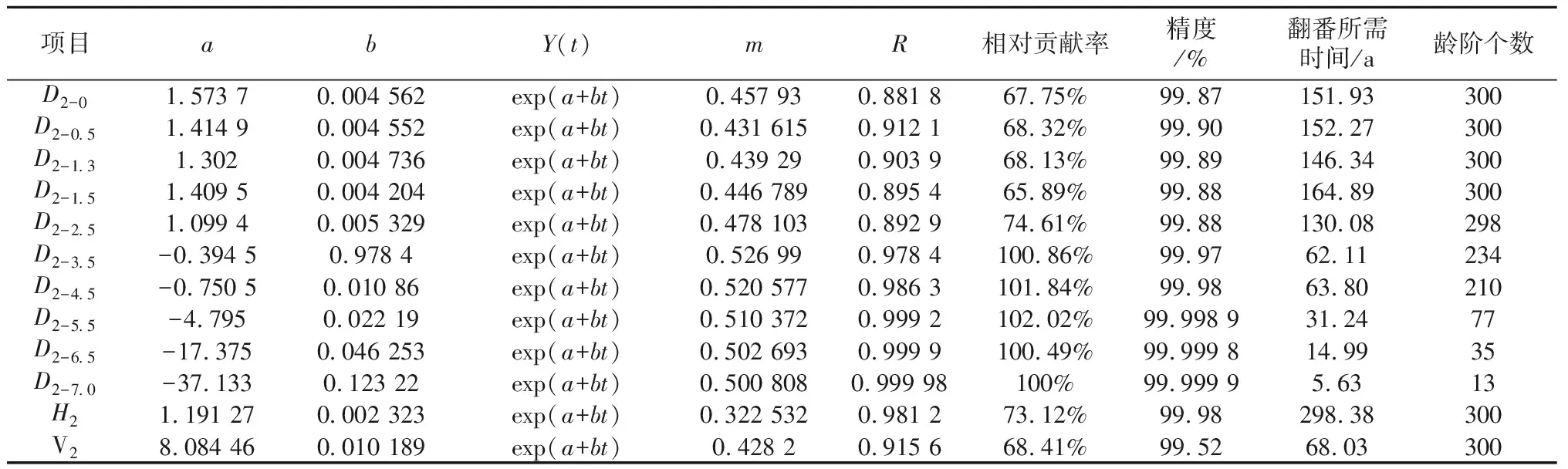
表7 300年生侧柏生长过程经验方程现实状态表(1a龄阶、成长方程)

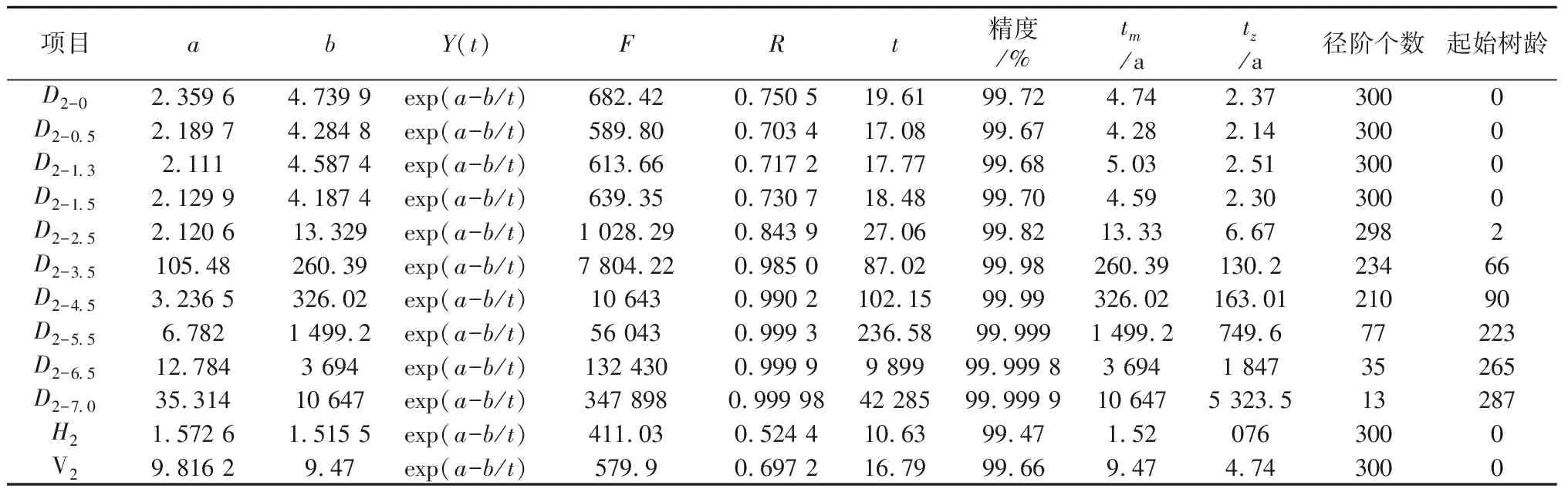
表8 300年生侧柏生长过程经验方程融合现实状态表(1a龄阶、阻力方程)

4 讨论

试验表明只要起始年龄一致，各样本按时间序列对应时间间隔一致，其平衡精度完全一样，相斥状态，试验精度的降低，表明经过一定系数的调整，阻力作用和成长作用达到平衡状态，说明试验的科学性和准确性。随着年龄的增加，时间因素生长贡献率增加，甚至达到100%。通过树木生方程的研究可以预测树木的期望寿命，随着树高的增加，树木长势提高，树木期望寿命有所提高。现实状态与平衡状态区别不大，二者可以互相取代。随着年龄的增长，树木的生长作用减弱，阻力作用增强。由于经费时间有限，不足之上在所难免，诚望有识之士多提宝贵意见，使该研究再上档次、上水平。