含储氢装置的分布式能源系统的优化经济调度
2019-12-06贾洋洋仲海涛张智晟
贾洋洋,仲海涛,张智晟
(1.青岛大学 电气工程学院,山东 青岛 266071;2.国网山东省电力公司泰安供电公司,山东 泰安 271000)
随着社会经济的飞速发展,人们对能源的需求不断增加,传统的供能模式单一,能源利用率较低且不易控制,运行成本受电价影响较大。以分布式电源为主体、冷热电联供的分布式能源系统,具有能源分级利用、安装地点灵活、易于控制、低碳环保等特性[1-2]。储能系统可以平抑可再生能源的出力波动,降低电网负荷的峰谷差,提高电网的运行可靠性[3-4],近年来得到了飞速发展。分布式能源系统的经济调度问题是分布式能源系统经济安全运行的关键,日益引起学术领域和工程应用领域的关注。陆月红等[5]采用混合整数非线性规划方法,解决了含有热能储存的建筑分布式能源系统的最优调度问题,并通过实际算例验证了热储能装置对分布式能源系统节约成本有着重要的作用。霍现旭等[6]对氢储能系统关键技术及应用综述进行了分析,提出:储氢装置能量密度高,运行维护成本低,能量存储时间较长且可实现无污染、零排放,是一种新兴的储能装置;该能量储备技术可存储100 GW·h以上能量,且可同时满足极短或极长时间的供电,是极具潜力的新型大规模储能技术。但是并没有用实际算例来分析氢储能对于节约分布式能源系统运行成本的问题。杨永标等[7]以天津中新生态城能源站冷热电联供系统(combined cooling,heating and power system,CCHP)为例,建立了含光伏和储能的CCHP调峰调蓄优化调度模型,分析了系统中的蓄能对调节电网峰谷差、增强电力系统运行灵活性的重要作用。基于这些,本文对含储能装置的分布式能源系统的经济调度问题进行研究,构建了含有分布式电源、储氢装置和冷负荷及电负荷的分布式能源系统的经济调度数学模型,采用粒子群优化(particle swarm optimization,PSO)算法、和声搜索(harmony search,HS)算法、以及改进的和声搜索算法对模型进行求解,并对比经济成本;并经实际算例,对本文提出的含储氢装置的分布式能源系统经济调度方法的可行性进行仿真验证。
1 分布式能源系统设备的数学模型
本文所研究的分布式能源系统主要设备包括微型燃气轮机、吸收式冷水机组、储氢装置、电制冷机、光伏机组等能量转换设备以及通信辅助设备,系统结构如图1所示。
1.1 微型燃气轮机
微型燃气轮机的发电功率
PMT(t)=qV,gas(t)ηMTLgas.
(1)
式中:PMT为微型燃气轮机的发电功率,kW;qV,gas为微型燃气轮机燃气消耗体积流量,m3/h;ηMT为微型燃气轮机发电效率;Lgas为天然气的低热值,Lgas=9.7 kWh/m3;t为时间。
1.2 吸收式冷水机组
吸收式冷水机组可充分利用微型燃气轮机产生的余热,提高能源的利用率,其制冷量
Qco(t)=QMT(t)ηreckco.
(2)
式中:ηrec为烟气余热回收率;制冷系数kco=0.95;QMT为微型燃气轮机的排气余热量。
微型燃气轮机的排气余热量及烟气余热回收率分别为:
(3)
(4)
式中:ηl为微型燃气轮机的散热损失系数,ηl=0.03,T0为环境温度;T1、T2分别为进出溴化锂制冷机的烟气温度[8-12]。
1.3 储氢装置模型
储氢装置主要由电解槽、氢气燃料电池和储氢罐3个部分组成。储氢装置系统是一种完美解决风光互补存储剩余低价能量的一种装置,它自身技术成熟可靠,应用于含有风光发电的分布式能源系统时,既有及时、高效、可长期储能的优势,又可以降低分布式能源系统的运行经济成本,达到零排放要求[13-15]。该设备可以从电网中获得剩余的电量作用于电解槽,产生氢气储存在氢气罐中;当电网中用电比较紧张时,燃料电池可以通过燃烧氢气罐中的氢气发电。通过储氢罐氢气储存量描述其数学模型为
SH(t+1)=

(5)
式中:SH为氢气存储状态;Pelz为电解槽耗电功率;ηelz为电解槽产氢效率;δelz、δfc分别为电解槽、燃料电池的开关状态;Pfc为燃料电池的发电功率;ηfc为燃料电池的发电效率[16]。
1.4 电制冷机
电制冷机的耗电功率与制冷功率关系式为
(6)
式中:PEC为电制冷机的耗电功率;QEC为电制冷机的制冷量;kEC为电制冷机的制冷系数,即
(7)
式中:kN为标准情况下的制冷系数;Tec,o为电制冷机出水温度,Tec,o=7 ℃;Tec,i为电制冷机进水温度[17]。
1.5 光伏机组
光伏机组受室外光辐射照度G与光伏电池板表面温度的影响[18],光伏机组发电功率为
(8)
式中:Pstc为标准测试条件(standard test condition,STC)工况下的最大输出功率;Tstc为STC工况下光伏电池表面温度,Tstc=25 ℃;PPV为光伏发电功率;Gstc为STC工况下的光辐射照度,Gstc=1 000 W/m2;k为温度功率系数,k=-0.004 7 ℃-1;T为光伏电池板表面温度。
2 含储氢装置的分布式能源系统经济调度模型
2.1 目标函数
含混合储氢装置的分布式能源系统经济调度模型的目标函数为运行成本J最小,运行成本包括微型燃气轮机成本JMT、与大电网的功率交换成本Jgrid、电解槽损耗成本Jelz和燃料电池损耗成本Jfc。目标函数为
J=JMT+Jgrid+Jelz+Jfc.
(9)
a)微型燃气轮机运行成本为
(10)
式中:Cgas为天然气的价格,Cgas=2.02 元/m3;Vgas为燃气消耗量。
b)电网功率交换成本为
(11)
式中:Cpur为购电价格;Ppur为购电功率;Csale为售电价格;Psale为售电功率。购电时电网交换功率Pgrid为正,售电时Pgrid为负,Ppur、Psale定义如下:
(12)
(13)
c)储氢装置成本。储氢装置成本主要包括电解槽和燃料电池的维护成本,开关损耗与负荷的功率波动会严重影响设备的使用寿命;因此,储氢装置成本如下:
(14)
(15)
式(14)、(15)中:JC,elz、JC,fc分别为电解槽、燃料电池成本;Helz、Hfc分别为电解槽、燃料电池使用寿命;Jo,elz、Jo,fc分别为电解槽、燃料电池的每小时经济成本;Jup,elz、Jdown,elz分别为电解槽的开启、关闭损耗;Jup,fc、Jdown,fc分别为燃料电池的开启、关闭损耗;Jυ,elz、Jυ,fc分别为电解槽、燃料电池由功率波动引起的成本损耗;υelz(t)、υfc(t)为电解槽、燃料电池功率波动;为方便控制电解槽和燃料电池的工作状态,引入新的辅助逻辑变量——开启σj,on与关闭σj,off(j{elz,fc})。电解槽和燃料电池的状态由式(16)、(17)决定。
σj,on(t)=max(δj(t)-δj(t-1),0).
(16)
σj,off(t)=max(δj(t-1)-δj(t),0).
(17)
电解槽和燃料电池功率波动
υj(t)=Pj(t)-Pj(t-1).
(18)
2.2 约束条件
含混合储氢装置的分布式能源系统经济调度模型需要满足以下约束条件,具体如下所示:
a)分布式能源系统电功率平衡约束为
PMT(t)+PPV(t)+Pfc(t)+Pgrid(t)=
Pload(t)+Pelz(t)+PEC(t).
(19)
式中Pload为负荷功率。
b)分布式能源系统冷功率平衡约束为
Qco(t)+QEC(t)=Qcouser(t).
(20)
式中Qcouser为冷负荷需求。
c)储氢罐氢气储存量约束为
SH,min≤SH(t)≤SH,max.
(21)
式中SH加下标min、max来分别表示储氢罐氢气储存量的最小、最大值,下文中的部分参数以此类推。
d)微型燃气轮机功率约束为
0≤PMT(t)≤PMT,max.
(22)
e)电网功率交换约束为
0≤δsale(t)+δpur(t)≤1.
(23)
式中δsale、δpur分别为买电、卖电状态,在某个时刻不能同时买与卖,最多只能有一个值取1。
Ppur(t)-Psale(t)=Pgrid(t).
(24)
Pgrid,min≤Pgrid(t)≤Pgrid,max.
(25)
f)储氢装置功率约束为:
0≤δelz(t)+δfc(t)≤1.
(26)
Pj,min≤Pj(t)≤Pj,max.
(27)
3 经济调度模型求解算法
本文建立的分布式能源系统优化调度模型是一个高维度非线性规划问题,不少常规优化算法都属于凸优化范畴,有唯一明确的全局最优点;而绝大多数智能优化算法针对的是多极值问题,通过有效设计可以在跳出局部最优和收敛到一个点之间有个较好的平衡,从而实现找到全局最优点。在电力系统优化调度问题中,粒子群优化算法、遗传算法等常用优化算法由于其较好的全局搜索能力得到了广泛应用;但相比粒子群优化算法与遗传算法等常规算法,和声搜索算法的原理更为简单,具有参数较少、通用性强、搜索速度更快、寻优能力更强的特点。因此,本文采用改进和声搜索算法对经济调度模型进行求解[19-24]。
3.1 和声搜索算法
和声搜索算法是一种新颖的智能优化算法,可以反复调整算法记忆库中的解变量,随着迭代次数的增加使函数值不断收敛,从而来完成优化。该算法概念简单,参数可调,易于实现。类似于模拟退火算法的物理退火模拟、遗传算法模拟生物进化以及粒子群优化算法模拟鸟群觅食等,和声算法模拟音乐演奏的原理。该算法模拟音乐创作的过程,其中音乐家使用他们自己的记忆来重复调整乐队中每个乐器的音高以实现美妙的和声状态。
算法流程如图2所示,具体的算法步骤可以描述为:
a)确定和声搜索算法的参数值:和声搜索存储器大小M、取值概率pHMCR、调整概率pAR、调整带宽BW、循环次数Tmax。
b)从和声X的解空间里随机生成X1,X2,…,XM共M个和声放入和声记忆库(harmony memory,HM),并记录对应的函数值f(X),和声记忆库的形式为
(28)
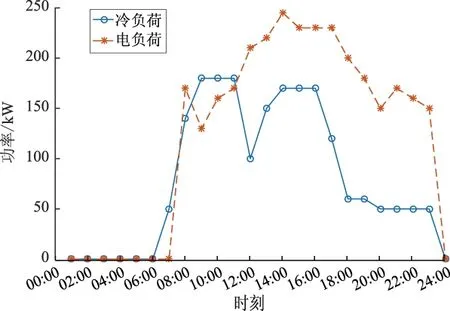
c)生成一个新的和声。①在[0,1]之间生成随机数r1并将其与pHMCR进行比较。②若r1 d)更新和声记忆库。对Xnew进行评估,即f(Xnew)。若优于和声记忆库中的函数值最差的一个,即f(Xnew) e)检查算法是否终止。重复步骤c)和d),直到创作次数达到Tmax为止。 图2 和声搜索算法流程Fig.2 Harmony search algorithm flow chart 由于常规和声搜索算法的pAR和BW都是以固定值来对新的解进行调整,这种参数更新形式严重影响和声搜索算法的寻优能力,并且可能会出现收敛不稳定的结果。基于此,本文提出自适应全局最优和声搜索算法,采用pAR和BW根据迭代次数的增加而减小的方式,对常规和声搜索算法进行改进,改进公式如下: (29) (30) 式中:N为最大迭代次数;i为当前迭代次数。 改进后的和声搜索算法充分利用了和声记忆库中的初始解信息,并以较大概率和带宽进行修正,增强了算法的全局搜索能力,提高收敛速度;并且随着迭代次数的增加,修正量变小,搜索范围变小,结果更为精确,提高了寻找最优解的概率。 本文算例取某综合楼分布式能源系统,该综合楼建筑面积为5 000 m2,主要设备包含微型燃气轮机、吸收式冷水机组、混合储氢装置、光伏电池和电制冷机等。以夏季某典型日的用电情况作为典型日进行仿真分析,该综合楼夏季典型日电负荷与冷负荷需求曲线如图3所示,夏季典型日光照强度和环境温度曲线如图4所示。 图3 夏季典型日电负荷与冷负荷需求曲线Fig.3 Electrical load and cold load demand curves in typical day in summer 图4 夏季典型日光辐射照度和室外温度曲线Fig.4 Solar radiation intensity and outdoor temperature curves in typical day in summer 微型燃气轮机最大功率PMT,max=200 kW,混合储氢装置、光伏电池、电制冷机等设备的参数有:①对于光伏电池板,PPV=15 kW,最大功率点工作电压Umax=18.5 V,最大功率点工作电流Imax=8.12 A;②对于电解槽,ηelz=7.3 kWh/m3,JC,elz=63.93 元/kW,Jo,elz=0.0156 元/h,Jup,elz=0.957 元/次,Jdown,elz=0.0482 元/次,Jυ,elz=0.39 元/h,Helz=104h;③对于燃料电池,Pfc=5 kW,ηfc=0.768 m3/kWh,JC,fc=233.32 元/kWh,Jup,fc=0.08 元/次,Jdown,fc=0.026 元/次,Jυ,fc=0.05 元/h,Hfc=104h,Jo,fc=0.008 元/h;④对于储氢罐,罐的容量V=11 m3;⑤对于电制冷机,PEC=70 kW,kEC=4.2。电价采用分时电价,见表1。 表1 分时电价表Tab.1 Time-of-use electricity price list 本文对以下4种用电情形进行仿真比较: 情形1:负载无序用电,微型燃气轮机与吸收式冷水机组不动作,光伏发电剩余电量直接全部卖出,储氢装置不动作,不经任何优化处理。 情形2:储氢装置随分时电价高低、光伏发电及微型燃气轮机功率大小而动作,采用改进粒子群优化算法进行优化。 情形3:储氢装置随分时电价高低、光伏发电及微型燃气轮机功率大小而动作,采用和声搜索算法进行优化。 情形4:储氢装置随分时电价高低、光伏发电及微型燃气轮机功率大小而动作,采用改进和声搜索算法进行优化。 4种情形的用电经济成本依次为2 728.00 元、2 326.82 元、2 153.22 元和2 111.37 元。情形2、情形3和情形4的仿真收敛曲线如图5所示。 可以看出,改进后的和声搜索算法比粒子群优化算法和常规的和声搜索算法的优化效果更好,能够更好地分配各微能源的出力,使得成本尽可能低。 由图5可以看出,粒子群优化算法的收敛速度最快,但是容易陷入局部最优解,使得最终的优化结果达不到理想最低状态;相比改进后的和声搜索算法由于能够产生多样的新解,大大提高了全局最优搜索能力,改进算法后优化效果更佳,成本也能达到最低。 图5 3种不同情形收敛曲线Fig.5 Convergence curves of three different situations 为验证储氢装置接入对分布式能源系统的影响,采用本文提出的分布式能源系统经济调度方法进行调度,各微能源出力结果如图6所示。 图6 各微能源出力结果Fig.6 Output result of each micro-source 由图6可知,由于综合大楼24:00—次日06:00为休息时间,电负荷和冷负荷需求低,而且电价比较低;所以该时间段微型燃气轮机并不工作,此时间段电价较低,储氢装置电解槽开始工作,将低电价的电能转化成氢气储存在储氢罐中。当综合大楼在07:00—17:00时开始工作,电负荷和冷负荷需求不断增大,达到用电高峰,此时间段电价达到峰时电价;因此微型燃气轮机开始工作,作为主要提供电能的设备,光伏机组开始工作产生部分电能作为辅助,且储氢装置电解槽处于关闭状态,燃料电池开始工作,将储存的氢气转化为电能提供给负荷,从而减少从电网的购电量,降低运行成本。18:00—22:00微型燃气轮机功率下降,光伏机组出力变为零,此时电负荷需求相对仍旧比较大,电价仍处于峰时电价;因此储氢装置燃料电池继续工作,提供部分电能来降低从电网的购电量,进而节省运行成本。22:00—23:00,此时用电高峰期结束,电价变成谷时电价;所以此时完全从大电网购电,用于电负荷和冷负荷的需求。从上述分析可知,储氢装置对电网调峰调蓄具有重要的作用,在用电低谷期且电价低时耗电储氢,在用电高峰期且电价较高时耗氢产电,从而缓减电力负荷的峰谷差,同时也降低了系统的运行成本;因此,本文提出的分布式能源系统经济调度方法是可行的。 本文对含混合储氢装置的分布式能源系统的经济调度问题进行了研究,构建了含有微型燃气轮机组、吸收式冷水机组、储氢装置、光伏机组、电制冷机以及其他通信辅助设备的经济调度数学模型,分别采用粒子群优化算法、常规和声搜索算法和改进和声搜索算法进行求解;实际算例仿真验证了储氢装置对于降低分布式能源系统的经济成本的有效性,验证了改进和声搜索算法收敛性能的优越性。该研究为分布式能源系统的建设提供了一定的理论支持。但本文提出的是日前调度模式,没有考虑到可再生能源及负载实时变化等不确定因素的影响,在以后的研究工作中应该进一步考虑。
3.2 改进和声搜索算法
4 算例分析
4.1 算例介绍


4.2 算例结果仿真分析


5 结束语
