火电厂AGC控制回路的非线性分析

欧阳春明，李慧霞，钱文华

（1.广东电网有限责任公司 电力科学研究院，广州 510080；2.北京协同创新智能电网技术有限公司，北京 100094）

0 引言

AGC是电网中发电机组调度与控制的一项重要内容，是实现电网有功功率控制、维持系统频率质量以及互联电网之间联络线功率控制的一种重要技术手段，其控制策略的优劣、模型辨识的精度等直接决定了AGC控制效果的好坏[1-4]。

正如非线性是任何系统都或多或少存在的特性一样，所有火电厂热工仪表、设备等也普遍轻重不一地具有非线性特性。诸如热电偶温度仪表中热电势和温度的关系、节流式流量仪表中流量与压差的关系都是非线性函数；火电单元机组包含由锅炉、汽包、再热器以及汽轮机等具有热惯性、反应延迟的设备[5,6]。由这些具有非线性特性的热工仪表以及设备所组成的AGC控制回路也必然存在一定的非线性特性，导致AGC控制回路的控制策略、建模等存在很大的难度。分析AGC控制回路的非线性特性能有助于明确其控制策略的制定、控制对象模型的辨识。

自回归各态历经ARX模型通过一个线性方程来描述系统输入输出之间的关系，被广泛应用于线性系统分析[7,8]。神经网络属于人工智能领域，具备自学习能力，尤其适用于非线性系统的分析，并得到快速发展[9]。本文主要介绍ARX和神经网络两种系统分析方法，并通过火电厂AGC控制回路实际运行数据进行实验分析，对两种系统分析方法进行比较，研究AGC控制回路的非线性特性。

1 ARX模型分析

离散系统的输入输出模型可用差分方程的形式来表示[10-12]：

对式（1）进行z变换，在零初始条件下输出变量的z变换对输入变量的z变换之比就是该系统的z传递函数：

式（2）中，z为移位算子，它与运算子s的关系为：

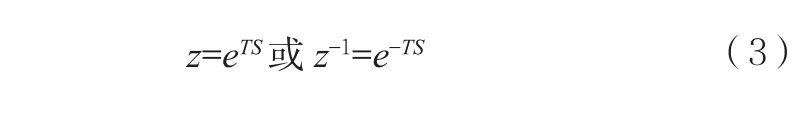
其中，T为采样周期。移位算子的运算有如下的关系：

利用式（4），可容易地将式（2）的z的传递函转换为式（1）的差分方程的形式。

式（5）中：

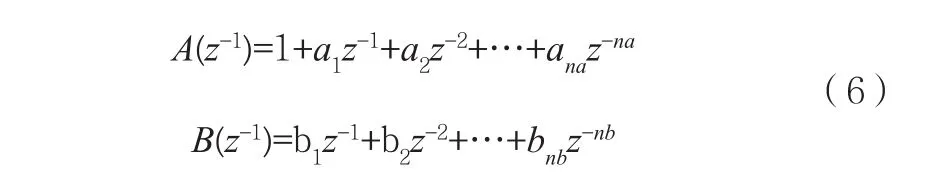
其中：na、nb和d是这类模型的结构参数，na、nb是A(z-1)和B(z-1)的阶次，d是纯滞后步数，纯滞后时间即为dT。

如果上述的模型还受到噪声的影响，则式（5）的模型可以进一步地写成随机性模型：

式（7）中：

式（5）是确定性定常线性系统离散时间模型，而式（7）是随机性定常线性系统离散时间模型。

式（7）通常使用最小二乘法进行求解，最小二乘法的一次完成算法如下，给定单输入单输出线性、定常、随机系统的数学模型：

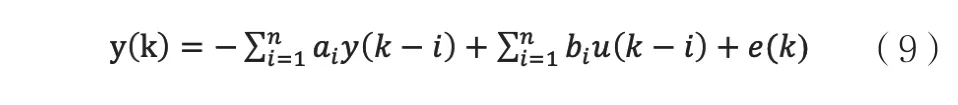
已知测量数据序列{u(k),y(k),k=1,2,…,n+N}，对式（9）所描述系统，辨识包括两个问题：首先要确定阶次n，这是结构辨识问题；在n确定后，求参数ai，bi这是参数估计问题。本文讨论的问题为n已知的情况。

随着方程（10）建立（y, x已知），能够利用最小二乘法估计参数矢量θ[13]。极小化误差函数J：

可得最小二乘估计值θ′=(X T X)-1X Ty，如果(X T X)是非奇异的，则此解存在。

2 神经网络系统分析

神经网络具有显著的学习能力和高度的并行运算能力，为非线性系统分析提供了一条十分有效的途径[14,15]。

针对火电厂具有大惯性、大延迟特性的热工对象[16,17]，可以尝试使用神经网络的方法来建立其数据模型。利用现场自然存在的扰动及被控对象的输出作为神经网络辨识器的输入，经过神经网络辨识器的学习过程，来获得系统的数学模型。

目前应用在系统辨识中的神经网络主要有以下3种：单层神经网、Adaline神经网络和B-P神经网络。

由于现场存在各种无法预测的干扰信号，许多系统中间状态的值是无法测量的，且系统阶次一般无法预先得知或无法辨识得非常准确，这就限制了单层神经网络在电厂中的应用[18]。

由于Adaline神经网络存在缺点：一是设定的延迟器数目必须与系统阶次相等，即系统阶次必须已知或者辨识得非常准确，才能获得满意的辨识结果；二是网络较脆弱、抗干扰能力差，这也限制了该网络在电厂中的应用。

1989年Robert Hecht-Nielson证明了对任何在闭区间内的一个连续函数，都可以用一个隐层的B-P网络来逼近，可以选用一个3层的B-P网络进行辨识试验。学习步长、辨识网络的输入层节点数、隐层节点数等会影响神经网络的辨识精度。设计一个广义的、适用的辨识网络基本结构、尽可能减少辨识参数的反复、交叉调整，以达到预期的辨识精度是基本设计思想。

图1 4500s实测数据下ARX和BP预测输出比较Fig.1 The output by ARX and BP neural network

图2 7200s实测数据下ARX和BP预测输出比较Fig.2 The output by ARX and BP neural network

表1 ARX和BP神经网络分析AGC回路数据结果比较Table 1 The analysis result with ARX and BP neural network

3 实验结果分析

设受控对象模型为：

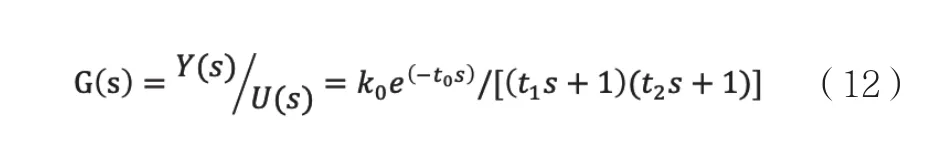
通过Z变换写成差分方程形式

t1，t2为时间常数；k0为模型增益；t0为纯滞后时间；n为采样点数(n=1,2,…)。

设纯滞后时间t0是采样周期的整数倍，即t0=m1T，由式（13）可知网络的输入节点数为4，即输入向量为p=[y(n-1)y(n-2)u(n-m1-1)u(n-m1-2)]，设隐层节点数目为4，一个输出节点，此时受控对象模型网络为4-4-1结构。

本文实验数据采用某电厂AGC汽机主控回路的实测数据，数据主要包含实测输出信号y、输入信号u和干扰信号d。

按照公式（7），将以上实测输出信号y、输入信号u和干扰信号d，通过ARX方法建立最优的模型，并得到仿真输出。

应用BP神经网络对实测输出信号y、输入信号u和干扰信号d进行训练，输入向量p=[y(n-1)y(n-2)u(n-1)u(n-2)d(n-1)d(n-2)]，学习速率l=0.005，采样时间间隔为1s。通过对网络训练可以得到对应的输出。

本文采用7组实测数组对以上两种方法进行比较，其中两组数据（数据长度分别为4500s和7200s）的仿真输出和实测输出的曲线图见图1和图2所示。从图中可以看出，通过BP神经网络辨识得到输出与实际输出曲线变化趋势更一致。

通过比较7组数组的仿真输出与实际输出的匹配度，以及仿真时长如表1所示。

从表1可以看出，对于同一组数据，使用BP网络进行系统分析得到的输出匹配度明显高于ARX方法，并且分析的速度也比ARX要快。随着数据长度的增加，ARX分析时间呈线性增长，而BP网络分析时间并不简单的随时间增长而增长，而是可能与数据的复杂度有关。

4 结论

本文通过ARX和BP神经网络两种方法，对火电厂AGC汽机主控回路实测数据进行了仿真分析，结果表明：BP神经网络能够更准确地分析和预测系统输出，并且分析速度快；ARX系统模型的分析时间随着数据长度的增加而呈线性增加；BP神经网络在进行系统分析时，其时间随着数据长度的增加而略微增加，甚至出现下降的情况，说明BP神经网络系统分析的时间除了和数据长度有关外，可能还与数据本身的复杂度有关。

综合以上，可以得出火电厂主控回路的数据分析使用BP神经网络这一非线性分析方法精度高、速度快，说明火电厂主控回路存在明显的非线性特性，使用二阶惯性延迟系统能够更好地描述火电厂AGC汽机主控回路的特性，在进行火电厂控制回路设计时应充分考虑其非线性。