基于U-Net的多图谱标签融合算法

2019-12-06芦玥，马瑜，王慧，王原

液晶与显示 2019年11期

芦玥，马瑜，王慧，王原

(宁夏大学物理与电子电气工程学院，宁夏银川 750021)

1 引言

人体脑组织主要包括有基底核与大脑皮层两部分，由一系列的神经核团组成的基底核位于大脑的深部，大脑皮层由覆盖于端脑平面的灰质以及皮层深部的白质组成。磁共振成像(Magnetic Resonance Imaging，MRI)可清晰地分辨脑部灰质、白质及其余各神经功能核团，其对比度特性丰富，细节精确，成为了医学临床中对脑功能研究、脑组织疾病预测、病灶确定及手术前中期辅助干预的主要手段。海马体主要负责人类的记忆、学习、情感控制以及空间方向定位。同时，许多神经系统疾病，如阿尔兹海默病、颞叶癲痫、精神分裂症以及抑郁症等，都与海马体形态体积的改变有关。通过对脑部磁共振像的海马体分割，实现海马体的精确分割并对海马体进行形态研究与体积的测量，对许多神经系统疾病的研究及进行分析诊断有着重要的意义。

人脑海马体形状、大小不规则，边缘模糊，难与其相邻组织进行区分，因此传统图像分割算法在海马体分割问题上，有着结果不理想、精确度下降等问题，同时，虽然手动分割的精确度较高，但耗时费力，缺乏重复性[1]。

众多学者在半自动与全自动分割海马体的方法上做了大量的研究[2]，Jack、Bentley等将阈值法与边界跟踪法结合应用，对海马结构进行了人机交互的半自动分割，验证了其精度和可重复性，结果证明这种方法具有较高的精度和可重复性[3]。Ashton等应用主动轮廓模型(Active Contour Model)即Snakes模型[4]，实现海马区的分割，此算法对目标起始轮廓的精度、位移不敏感[5]。Kelemen等提出了一种弹性变形表面模型(Elastically Deformabel Surface Model)，将弹性变形表面模型作为已分割图像的模型，能实现对海马体的自动三维图像分割，用弹性变形表面模型进行海马体分割，具有自动、快速、精确的特点，应用前景广阔[6]。最近几年，基于模型分割已经成为热点，比如，Cremers提出用高斯函数训练数据然后用其作为模型[7]，Zhang[8]应用密度和几何信息来控制在水平集下的曲线演化，Dambreville提出的卷积核碎片分析对几何动态边界引进形状优先[9]。然而，这些先前的工作通常需要人工获得训练数据，而且需要做多次参数评估，这些都加大了算法的运算代价，在分割精度上也有待提高。

自2012年起，卷积神经网络在图像分类和图像识别检测方面被广泛应用并取得了巨大的成就，而全卷积神经网络(Fully Convolutional Networks,FCN)[10]将神经网络的图像级别分类扩展到像素级别的分类。FCN既可以接受任意大小的输入图像而不用要求训练图像和测试图像具有相同尺寸，又实现网络的高效性。

U-Net网络[11]借鉴了FCN的设计思想和相关方法实现语义分割，更加适合用于医学图像的分割。本文对U-Net网络的卷积层数及网络架构进行优化改进，将其应用到多图谱的标签融合分割中，进一步提高海马体分割的精度及效率。

2 图像预处理

2.1 颅骨剔除

图1 人体大脑MRIFig.1 Human brain MRI

人脑MRI中背景和非脑组织占有较大比重，容易造成配准的误差，人体大脑MRI如图1所示。剔除脑壳是重要的预处理工作，本文利用Bauer[12]提出的Brain Surface Extractor(BSE)算法剔除脑壳，克服了传统BET算法运算时间长的缺点,并可以有效剔除影响配准精确度的脑壳与背景部分。BSE算法利用高斯拉普拉斯边缘检测算子(Laplacian of Gaussian，LoG)基于二阶导数的边缘检测方法，将高斯平滑滤波器和拉普拉斯锐化滤波器相结合，首先对图像进行高斯平滑滤波，在平滑图像的同时降低噪声，然后计算拉普拉斯(Laplacian)二阶导数，通过零交叉(Zero crossings)获得图像或物体的边缘，最后根据形态学知识在不改变脑部内部结构的同时将颅骨剔除。人脑MRI图像如图2所示，剔除颅骨后的人脑MRI图像如图3所示。

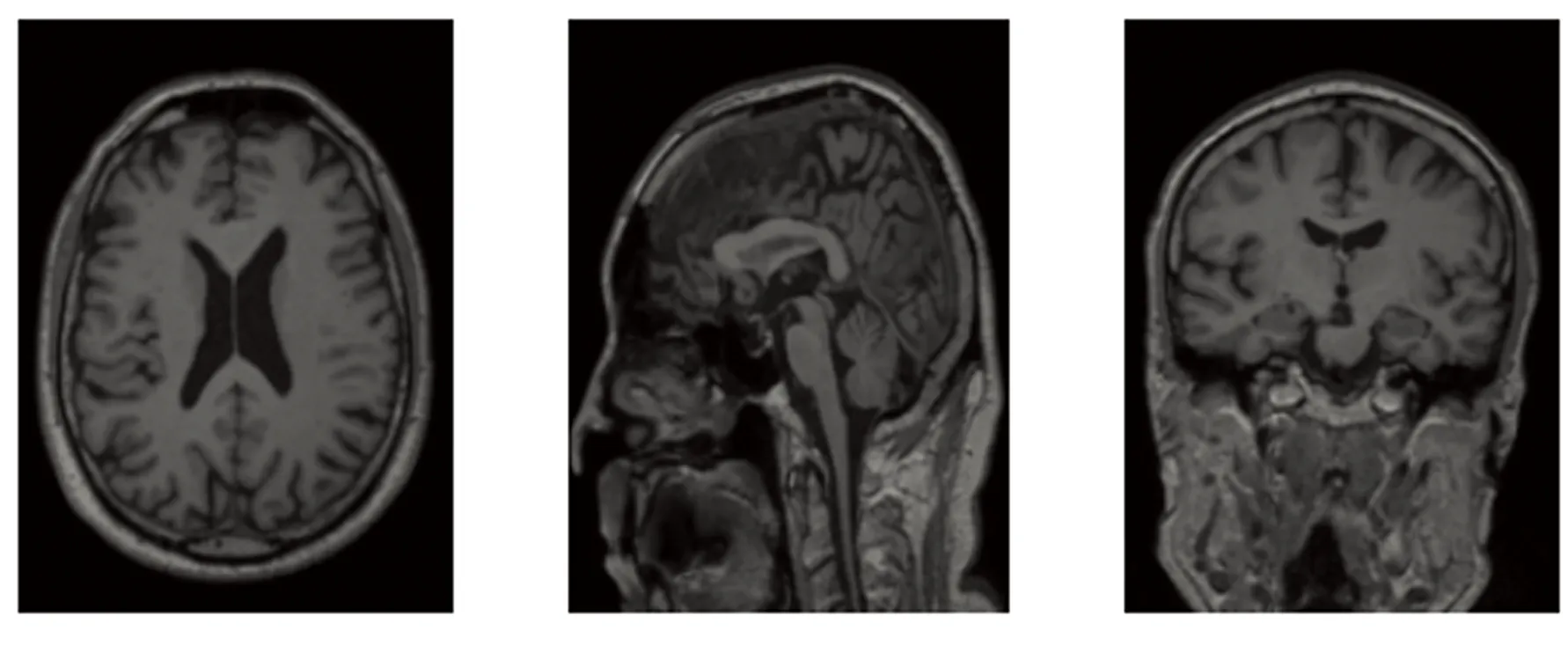
图2 人脑MR图像Fig.2 Human brain MR images

图3 剔除颅骨后的人脑MR图像Fig.3 Human brain MR images after skull-stripping

2.2 提取待分割组织ROI

在脑部MRI中，海马只是众多脑部核团之一。实验中发现，在图谱选择过程中，相似的解剖结构会对图谱的选择造成影响，从而干扰图谱选择结果。通过分析图谱选择算法及其误差，发现影响分割效果的一个重要因素是感兴趣区域的选取。对于原始的图谱选择算法，其计算空间往往是整个图谱，图谱选择效果欠缺。海马体是一个较复杂的结构，事实上，即使两幅图谱比较相似，但受到周围体素或者其他相似组织的影响，海马体的相似性也可能较小，从而影响海马的提取。医学图像提取感兴趣区域(Region of Interest，ROI)是指在专家手工标记的标签图像中找到海马体所在区域，即感兴趣的结构，以此结构为中心，利用包围盒算法获得一个完全包含该结构的最大连通区域，并根据此区域提取图像块，利用该图像块进行后续的配准、分割等操作。因此，针对上述问题，本文采用基于ROI的图谱选择算法，与传统算法不同的是，不再利用整个图谱图像进行互信息相似性计算，而是在利用包围盒算法提取ROI之后，计算图谱的互信息、梯度相似性选择图谱。

本文在配准之前粗略地提取ROI，两个图库分别为50×63×60和60×74×67的立方体箱。本文图库1以灰度图a01、标记图a01-seg为参考图像，对图谱进行以参考图像为基准的重采样操作。参考图像的尺寸大小为189×233×179，体素间距是1×1×1，图像中心为98×134×72。例如，当图谱a01的尺寸大小、体素间距、图像中心分别为189×233×179、1×1×1、97×135×70，则重采样后a01具有和参考图像一样的

图4 以左、右海马体为中心提取ROIFig.4 Extracting ROI centered on the left and right hippocampus

大小、间距、图像中心，能够有效减少图谱配准运行时间，改善配准的精度。图4(a)是以左海马体为中心初次提取ROI，图4(b)是以右海马体为中心初次提取ROI，大小为50×63×60的灰度图谱及对应的标记图像图谱块。

2.3 图谱选择

MAS中，Aljabar等人[13]在研究中发现，MRI的分割精确度并不随图谱数量的增多而提高。典型的MAS算法的计算时间是与图谱的数量线性相关的，因此从大量的图谱中选择合适的图谱子集可以有效提高算法速度。其次，通过排除可能误导分割的无用图谱，可提高最终分割的准确性。

本文采用归一化互信息(Normalized Mutual Information, NMI)与图像梯度计算相结合对待分割MRI与其他MRI进行相似性计算，NMI源于信息熵的概念，用来度量两个变量之间相互关联的程度。互信息可以描述不同系统之间的相关性，互信息值越大，表示系统之间的相关性越大，或一个系统包含另一个系统的信息越多。在人脑MRI分割中，由于各图谱图像都包含有相同的脑结构解剖信息，所以当两幅图像的空间位置一致时，对应像素灰度的互信息值最大。运用NMI来度量3D ROI的相似度值，其公式如下：

KNMI(a,b)=(H(a)+H(b))/H(a,b)，

(1)

(2)

(3)

其中：a、b分别表示两幅MR图像，ia、ib分别表示a与b的像素值，k为总的像素个数。

图像梯度算法考虑到每个像素邻域的灰度变化，利用一阶或二阶导数计算邻域像素值的变化规律，当图像中某一邻域灰度值变化较大时，该邻域一定有较大的梯度值，即该邻域具有边缘特征，否则邻域灰度值变化小，图像较平滑。

以NMI与梯度相结合来计算目标图像与图谱图像的相似度，选择与目标图像最相似的图谱作为最终的融合图谱，Awate[14]等人2012年的研究表明，选择图谱的最佳数量为10个左右。由此本文将从两个图库中分别选择10幅相似度最高的图谱图像。

3 多图谱配准

基于多图谱分割算法的两个关键步骤分别是图像配准与图像融合。精确的配准结果使得形变后的图谱图像对应的标记图像与待分割图像中的海马体在形状、体积、大小方面更相似。

3.1 重采样原理

由于3D医学图像数据规模大，图像间的配准过程所需时间过长，传统“粗精”混合的配准方法不能同时达到高精度、高效率的要求。所以本文利用重采样的方法代替“粗”配准阶段[15]，重采样过程包括输入图像、变换和校对，图像的空间坐标通过变换进行映射以便生成一个新的图像。重采样使图谱图像和目标图像有相同的空间采样点和采样点空间距离，同时减少了“粗”配准环节所需时间。进行重采样后，调整了浮动图像和参考图像采样点不一致的问题，并且图像的尺寸大小得到矫正，为后续进行非刚性配准做好准备。图5是一个简单重采样的原理图，重采样涉及从原始图像中提取像素的位置、插值灰度级，并将其重定位到校正图像中的近似矩阵坐标位置。如图5所示，第一行是原图像素空间采样点、采样空间大小示意图，第二行是对图像像素进行重采样，改变原点坐标且采样空间大小为原来的两倍的图示。

图5 重采样原理示意图Fig.5 Schematic diagram of resampling

3.2 微分同胚Demons算法

以重采样结果取代刚性配准环节，并以提取的ROI作为微分同胚Demons配准对象，大幅度缩短配准时间。微分同胚是可逆的光滑映射，微分同胚Demons算法[16]，能够保证图像的拓扑结构在配准前后保持不变，光滑且连续，并防止引入形变折叠，对大小形变都适用，在缺少可用的空间变换信息时，是很好的配准框架。

微分同胚Demons算法，将Demons的变换空间利用公式c←s∘exp(u)转换到微分同胚变换空间(李群)中来优化目标能量函数。微分同胚Demons算法的目标能量函数为：

(4)

其中，变形场u是一个稠密速度场：

(5)

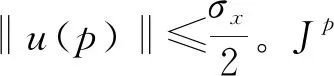
图6 待配准图像映射到目标图像的变形域Fig.6 Deformation domain of the registration image to the target image

微分同胚Demons算法的实现过程：

Step2：对u进行流体正则化，即u←Kfluidu；

Step3：利用牛顿方法计算李群得到的exp(u)，计算c←s∘exp(u)；

Step4：对s进行扩散正则化，s←Kdiffs。

如图6所示，为微分同胚Demons配准产生的一个形变场的示意图。

4 基于U-Net改进的标签融合算法

图像融合是指将待分割图像的若干标记图像数据进行有效信息的最大限度提取，综合成一个高质量的图像。采用融合技术对若干形变后的标记图像进行融合，能有效提取每个配准后的图谱图像中的有用信息，融合获得最具代表性的结果，所得的清晰准确的综合图像作为待分割图像最终分割的海马体，可有效提高算法整体的精确度。

常用的融合算法有多数投票表决法(Majority Voting, MV)[17]按照少数服从多数的准则决定最终的融合标记值，它是一种最简单最直接的融合方法。加权表决法(Weighted Voting Method, WV)[18]根据图谱与目标图像的相似性分配权重，分割精度优于多数表决方法。Warfield等人提出的STAPLE( Simultaneous Truth and Performance Level Estimation)[19]算法将每一个图谱看作一个弱分类器，利用EM算法计算每一个图谱的权重系数，加权平均后得到分割结果。另外基于非局部均值的块加权方法( Patch-based Method，PBM)算法[20]等较为常见，本文采用改进的U-Net网络图谱融合算法实现海马体分割。

4.1 U-Net网络

U-Net网络是基于FCN的设计思想和相关方法，在语义分割上更加简单明确，适合用于医学图像的分割。在ISBI Cell Tracking Challenge 2015上，U-Net网络取得了最优分割效果。在该任务中，训练集中只有30幅512×512果蝇第一龄幼虫腹神经(VNC)的电镜图像，针对该数据集的平均交并比(Intersection over Union, IOU)比第二名算法超出31%，在其他数据集上也要普遍比第二名高10%以上。

U-Net在结构上左右对称，形似英文字母“U”。一条为压缩路径，另一条为扩展路径。U-Net为了能精准地定位，收缩路径上提取出来的高像素特征会在上采样(Upsampling)过程中与新的特征图(Feature map)进行结合，以最大程度地保留前面下采样(Downsampling)过程一些重要的特征信息。而为了能使网络结构能更高效地运行，结构中没有全连接层(Fully Connected layers)，这样可以很大程度上减少需要训练的参数，并得益于特殊的U形结构可以很好地保留图片中的所有信息。

4.2 改进U-Net网络

U-Net网络中，压缩路径的结构和卷积结构相同，每两个3×3的卷积层后会跟一个2×2的最大池化层(步长为2)，并且每个卷积层后面采用ReLU激活函数来对原始图片进行下采样操作，在每个下采样的过程中，将特征通道数加倍。扩张路径中的每一步都包括上采样，每一步会有一个2×2的卷积层(激活函数也是ReLU)和一个两个3×3的卷积层。与此同时，每一步的升采样都会加入来自相对应收缩路径的特征图。在最后一层，本文采用将网络输出的的特征图输入到分类子网络，用Softmax函数将特征图谱映射到目标的类别数目上。最终，U-Net的整个网络一共有23层卷积层。左侧是传统的CNN架构，每经过卷积层和池化层，特征图的尺寸就会缩小。在右侧则加入了反卷积层进行上采样，用于扩大特征图的尺寸。左右两侧的特征通过Skip连接进行通道堆叠。图7为改进后的U-Net网络结构示意图。Softmax函数如式(6)所示：

(6)

其中j=1,…,K。

图7 改进后的U-Net网络结构示意图Fig.7 mproved U-Net network structure diagram

U-Net展现出了良好的特性，并且十分适合于生物医学领域，由于医学影像相对较少，因此本文进行了数据预处理的增强，使U-Net能够发挥的更加出色，本文将MRI数据集在改进的U-Net上进行训练，以半监督学习方式对网络进行监督，使用训练后的模型对MRI数据进行融合。根据海马体的目标图像，利用浮动图像对标记图像进行融合，融合结果即最终分割结果。U-Net网络对输入图像及其相应的浮动图像采用随机梯度下降法进行训练。参数更新如式(7)所示：

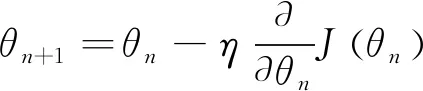
(7)

4.3 基于U-Net网络改进融合的MAS算法流程图

实验主要流程包括：

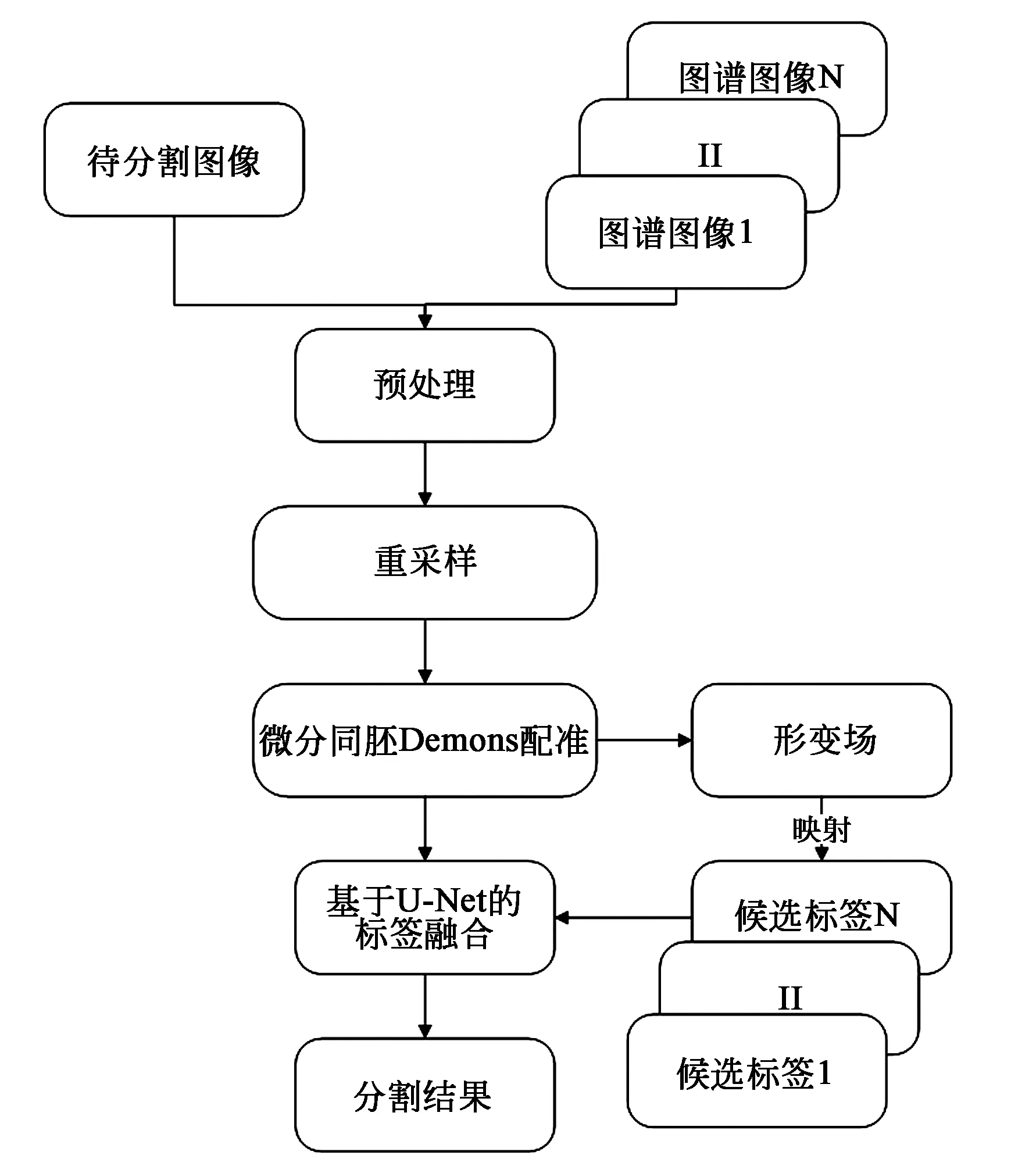
图8 实验流程图Fig.8 Flowchart of experiment

(1)对图像进行预处理，将所有图像进行颅骨剔除，再根据海马体的位置提取ROI，减小图像块包含的信息，提高整个流程的效率。

(2)相似性计算，利用互信息及梯度选择10幅最接近目标图像的磁共振图像作为浮动图像。

(3)对待分割图像与图谱图像的标记图像分别进行重采样及微分同胚Demons配准，使得所有图像的灰度值和对比度处于同一水平。

(4)分别对每组的10个图谱图像的海马体分割结果进行融合，获得一个与金标准最为接近、最精确的海马体分割结果。

(5)绘制各算法所得海马体的Dice相似性测度[24]值盒状图，直观展示各算法的融合精度。

5 实验结果与分析

本文釆用基于U-Net的多图谱标签融合算法，实现人脑MRI中海马体的自动分割。本次实验采用两个人脑磁共振数据库分别进行实验，图库1来自于伦敦帝国理工学院医学脑部研究数据库(Brain-development. Brain atlases)[21]，包含了20个图谱图像样本，其对应的标签图像标记了67个脑部结构。图库二来自于ADNI(The Alzheimer’s Disease Neuroimaging Initiative, ADNI)包含124个T1-MR样本的子库(The Alzheimer’s Disease Neuroimaging Initiative)[22]。两组实验结果进行比较实验，采用重采样及微分同胚对图像进行配准后，分别使用MV算法、WV算法、STAPLE算法、PBM算法及改进算法对标记图像进行融合。本文实验所需的软件工具包括Cmake跨平台编译器、Visual Studio 2010集成开发环境、ITK(Insight segmentation and Registration Toolkit)图像分析工具库[23]、ITK SNAP医学图像可视化软件、anaconda、Pycharm、MATLAB等。

在实现海马体的分割后，需釆用合适的评价方法对相关算法的性能及有效性进行评价。本文采用Dice相似性测度[24]对最终分割结果与金标准的重叠率进行比较，对实验结果实现定量分析。

此外，5种比较算法都将分别进行10组实验，并绘制各实验结果的盒状图，直观显示不同算法分割结果数据间的差异，预处理图谱选择阶段中选取10幅最优质磁共振图像，同时选取合适的目标图像，实验中共300个配准结果，50个最终分割结果。

实验结果如图9所示，分别为图库1、图库2目标图像左海马体的金标准(专家手动分割结果)与本文方法分割结果比较图：第一列之第三列图形分别为轴状位、矢状位、冠状位海马体切片图。(a)、(c)白色图形为目标图像的金标准，(b)、(d)红白相间图形为分割结果与金标准的结果重叠比较图，其中红色区域为两者重合区域，白色区域为两者非重合区域。由于图库图像标准不同，为更清楚表示图像特征本文分别取图库一左海马体取x=17，y=42，z=23截面，图库二左海马体取x=22，y=25，z=26截面，下同。将分割结果与MV、WV、STAPLE、PBM标签融合方法进行了分析对比。

图9为图库1、2中专家手动分割海马体与分割结果的比较图，白色区域为专家手动分割，红色区域为实验结果重叠部分，从图9(b)、(d)可以看出实验结果与金标准重合部分较多，图库1出现过分割现象，图库2分割结果良好。

(a) 图库1专家手工分割的左海马体(a)Experts manual segmentation of hippocampus in database 1

(b) 图库1分割结果切片比较图(b) Slice comparison graph of segmentation result in database 1

(d) 图库2分割结果切片比较图(d)Slice comparison graph of segmentation result in database 2图9 海马体分割结果与金标准切片比较图Fig.9 Comparison slices of hippocampus segmentation results with gold label

不同融合方法的融合结果在提取感兴趣区域的图像块中的示意图，如图10所示。

图10分别为图库1中专家手动分割切片、MV、WV、STAPLE、PBM及本文算法各分割结果在感兴趣区域图像块中的展示结果。

图11为图库2中专家手动分割切片结果、MV、WV、STAPLE、PBM及本文算法各分割结果在感兴趣区域图像块中的展示结果。

(a) 专家手工分割的左海马体(a)Segmented manually of left hippocampus by experts

(b) MV融合方法分割的左海马体(b)Segmentation of left hippocampus by MV fusion method

(d) STAPLE融合方法分割的左海马体(d) Segmentation of left hippocampus by STAPLE fusion method

(e)PBM融合方法分割的左海马体(e) Segmentation of left hippocampus by PBM fusion method

(f) 本文算法分割的左海马体(f) Segmentation of left hippocampus by our algorithm图10 专家手工分割及各算法分割人脑左海马体结构的结果(图库1)Fig.10 Artificial segmentation of left hippocampal structure by experts and segmentation results by various algorithms (database 1)

(a) 专家手工分割的左海马体(a)Segmented manually of left hippocampus by experts

(b) MV融合方法分割的左海马体(b)Segmentation of left hippocampus by MV fusion method

(d) STAPLE融合方法分割的左海马体(d) Segmentation of left hippocampus by STAPLE fusion method

(e)PBM融合方法分割的左海马体(e)Segmentation of left hippocampus by PBM fusion method

(f) 本文算法分割的左海马体(f) Segmentation of left hippocampus by our algorithm图11 专家手工分割及各算法分割人脑左海马体结构的结果(图库2)Fig.11 Artificial segmentation of left hippocampal structure by experts and segmentation results by various algorithms (database 2)

(a) MV融合方法与专家手工分割左海马体结构对比(a) Comparison slices of hippocampus segmentation results by MV with gold label

(b) WV融合方法与专家手工分割左海马体结构对比(b) Comparison slices of hippocampus segmentation results by WV with gold label

(d) PBM融合方法与专家手工分割左海马体结构对比(d) Comparison slices of hippocampus segmentation results by PBM with gold label

(e) 本文算法与专家手工分割左海马体结构对比(e) Comparison slices of hippocampus segmentation results by our algorithm with gold label图12 各融合算法与专家分割结果对比(白色表示专家手工分割，红色表示各算法分割结果，图库1)Fig.12 Comparison slices of hippocampus segmentation results by various algorithms with gold label (White represents expert manual segmentation and red represents segmentation results of each algorithm. database 1)

(a) MV融合方法与专家手工分割左海马体结构对比(a) Comparison slices of hippocampus segmentation results by MV with gold label

(b) WV融合方法与专家手工分割左海马体结构对比(b) Comparison slices of hippocampus segmentation results by WV with gold label

(d) PBM融合方法与专家手工分割左海马体结构对比(d) Comparison slices of hippocampus segmentation results by PBM with gold label

(e) 本文算法与专家手工分割左海马体结构对比(e) Comparison slices of hippocampus segmentation results by our algorithm with gold label图13 各融合算法与专家分割结果对比(白色表示专家手工分割，红色表示各算法分割结果，图库2)Fig.13 Comparison slices of hippocampus segmentation results by various algorithms with gold label (White represents expert manual segmentation and red represents segmentation results of each algorithm. database 2)

图12为图库1中各融合算法与金标准的对比图，可以看出MV算法分割结果不佳，分割出的海马体结构出现了不连续的现象，分割结果不完整，与金标准相差较大，WV算法海马体结构边缘超出专家手工分割海马体结构的边缘，出现过分割的现象。STAPLE算法在海马体边缘部分未重叠部分较多，边缘分割较差，PBM算法在传统方法切片比较中最优，但本文算法在细节处相较于传统算法更优。

图13为图库2中各融合算法与专家手动分割海马体切片比较图，可以看出MV分割效果较差，与金标准比较重叠部分相对较少，WV分割结果出现过分割现象，STAPLE融合方法分割的海马体，边缘结构较模糊，PBM融合方法分割结果与金标准比较接近，但本文算法相较于传统算法效果更优。

本文利用相似性测度值(Dice)评价分割结果与金标准的重叠程度，判断融合算法的优劣，Dice值取值在0～1之间，Dice值越接近1就表示融合结果与专家手动分割结果相似度越高，分割越准确，融合算法越好。基于U-Net网络得到的分割结果与目标图像的金标准进行相似性测度，并与MV、WV、STAPLE、PBM算法进行对比，结果如表1所示。

表1 不同融合方法的分割结果与金标准的Dice值(图库1)

Tab.1 Dice values comparing the segmentation results of different fusion methods with the gold label (database 1)

各方法Dice值左海马右海马MV0.829 40.820 8WV0.846 50.852 2STAPLE0.848 50.846 8PBM0.852 00.864 2本文算法0.887 00.876 1

表1和表2分别显示了图库1、图库2中MV、WV、STAPLE、PBM和本文融合方法分割人脑MR图像左、右海马体结构同金标准的相似性测度Dice值。由表可知，本文算法对两个图库人脑MR图像的分割结果与MV、WV、STAPLE、PBM融合方法相比，均有一定程度的提高。利用本文算法对图库1进行海马体分割的实验，分割精度相比于4种算法分别提高了约0.1，0.08，0.07，0.05，本文算法对图库2进行海马体分割的实验，分割精度相比于4种算法分别提高了约0.09，0.07，0.06，0.04。本文算法的分割结果与金标准相似度最高，分割结果最好。由于图表仅为一组数据实验结果，不能清楚直观地表现出各算法的稳定性，因此将所有实验结果绘制盒状图，如图14、15所示。

表2 不同融合方法的分割结果与金标准的Dice值(图库2)

Tab.2 Dice values comparing the segmentation results of different fusion methods with the gold label (database 2)

各方法Dice值左海马右海马MV0.829 80.823 2WV0.852 70.856 5STAPLE0.842 50.858 4PBM0.867 30.872 2本文算法0.891 50.904 9

盒状图分别显示了各算法分割结果相似性测度值Dice值的最小值(min)、下四分位数、中位数、上四分位数、最大值(max)以及异常点，盒状图能反映多组数据的整体特性。图14(a)为图库1中各算法左海马体分割的10组数据盒装图，从图中可以看出，MV算法效果较差，最小值0.78，最大值0.85，均值0.83，数据不集中，算法对不同目标图像分割不稳定。WV算法最大值0.86，最小值0.8，均值0.84，下四分位较MV相对低，上四分位较MV高，说明WV数据低精度较多，海马体间Dice值相差较大。STAPLE算法Dice值出现异常点，上四分位较高说明分割精度较高。PBM算法整体较稳定，最大值0.87，最小值0.83，均值0.85，分割精度均匀分布，算法较稳定。本文算法整体精度提高，分割精度稳定，最大值0.88，最小值0.84，算法整体性能都有提高。图14 (b)为图库1右海马体各融合算法盒状图，本文算法相较各传统算法整体精度提高，稳定性提高。图15显示了图库2中各融合算法左右海马体Dice值的盒状图，由盒状图可以看出本文所提算法分割精度相比于其他算法都有一定程度的提高，且数据相对稳定，具有良好的性能。

(a)左海马体的盒状图(a) Box plot of left hippocampal

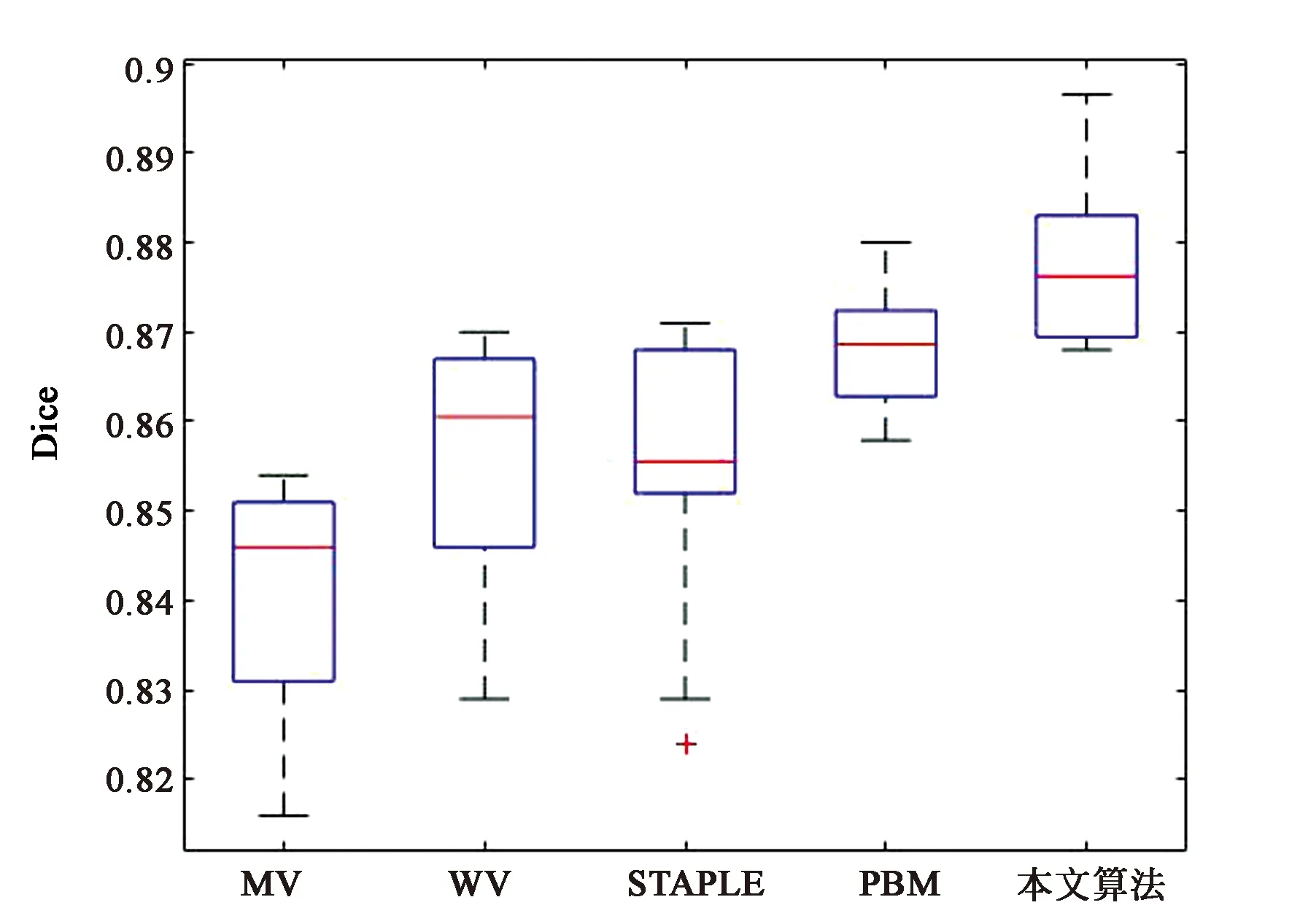
(b)右海马体的盒状图(b)Box plot of right hippocampal

(a) 左海马体的盒状图(a) Left hippocampal box plot

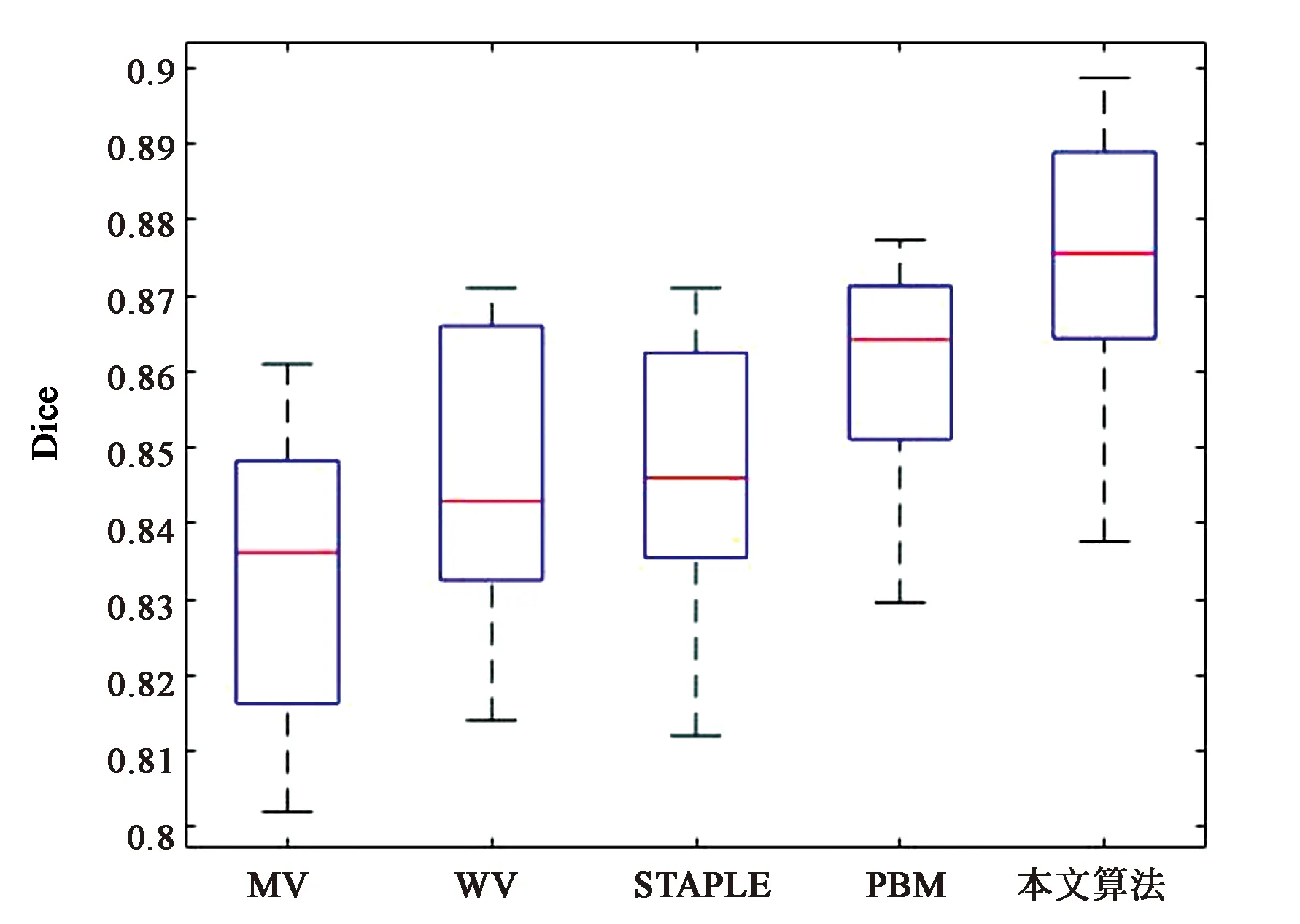
(b) 右海马体的盒状图(b) Right hippocampal box plot

6 结论

为提高多图谱MR海马体分割算法精度，本文提出一种基于U-Net网络改进的多图谱医学图像分割融合算法。在图谱选择阶段，利用提取感兴趣区域之后的图谱块进行图谱筛选，将筛选出的图谱用作浮动图像进行后续的配准、分割。在配准阶段，使用重采样代替“粗配准”减少配准算法所需时间，并利用微分同胚Demon算法进行“精配”实现图谱图像与目标图像的契合。在融合阶段，U-Net网络的加入确保了网络的监督学习，确保精度的同时提高分割算法效率。实验结果表明，本文算法相比于MV、WV、STAPLE和PBM在分割精度上提高了5%～10%左右，与金标准更接近。