一种基于BP神经网络的地区用电量预测方法研究
2019-12-05章熙郭翔万会江吴佩泽陈鹏陈佳捷
章熙 郭翔 万会江 吴佩泽 陈鹏 陈佳捷
摘 要:文章选取江苏省年用电量数据,提出了一个灰色系统理论与BP神经网络相结合的用电量预测方法。结果表明,该方法在用电量预测上精度较高,并且计算方便,可供有关部门参考。
关键词:用电量预测;反向传播神经网络;灰色关联分析
1 用电量的预测重要性介绍
地区电网用电量预测是指根据当地个人及企业用户的电能需求,在对历史数据进行研究的基础上,对地区用电量作出合理预估,供有关部门在规划工作时参考。准确的电量负荷预测有助于电网企业建立合适的运营策略,是制定电力发展规划的重要依据。因此,用电量预测是电网企业十分重视的一项工作,预测结果可能直接影响企业效益。准确的预测用电量对合理设计电网改造、错峰用电、发电计划有着重要的参考价值,有助于建立节能社会、促进地区经济的可持续发展。
关于用电量的预测方法有很多,传统方法有基于历史数据统计的线性回归预测算法[1],时间序列预测方法[2],灰度模型组合预测法[3]。近年来,随着机器学习算法研究的不断深入,出现了基于机器学习的算法,如神经网络[4]、支持向量机[5]、粒子群算法[6]、遗传算法[7]等智能预测方法。本文采用灰色关联度与反向传播(Back Propagation,BP)神经网络相结合的方法,以江苏省为例,利用Matlab软件对地区用电量进行预测、分析研究。
2 基于BP神经网络的地区用电量预测
本文提出一种灰色系统理论与BP神经网络相结合的地区用电量预测方法:先采用灰色关联分析法对影响因素进行筛选,选出关联度大的因素作为输入,以精简BP神经网络预测模型;再利用相关历史数据,对预测模型进行训练,实现对用电量预测的目标。
2.1 用电量影响因素灰色关联度分析
为了增加地区用电量预测的准确性,本文选取了6个对用电量影响较为明显的因素,即地方生产总值、人均收入、总发电量、能源消费总量、固定资产投资总额以及居民消费水平,并通过得到灰色关联度大小判断其相关程度。本文以江苏地区为例,查阅《江苏省统计年鉴》,得到从1999—2017年间6个影响因素和江苏省年用电量的统计数据进行定量分析。
利用灰色关联度理论分析用电量的6个影响因素,得到每个影响因子与用电量之间的关联度系数,具体步骤如下:首先,确定特征序列和因素序列,本文以用电量为特征序列,记为x0(t),选取影响用电量的6个因子为因素序列,记为xi(t)。其次,将因素序列进行归一化后,计算出因素序列与特征序列的差序列Δoi(k),找出两极差最大值M与最小值m。最后,计算灰色关联系数和灰色关联度,特征序列与因素序列在第k点的关联系数为:
利用上述公式计算得出年用电量与6个影响因素的相关联程度如表1所示。从表1可以看出,江苏省年发电量、居民消费水平、地区生产总值这3个因子与地区用电量之间关联度相对较大,因此,将其作为决策变量输入到BP神经网络预测模型中。
2.2 BP神经网络训练
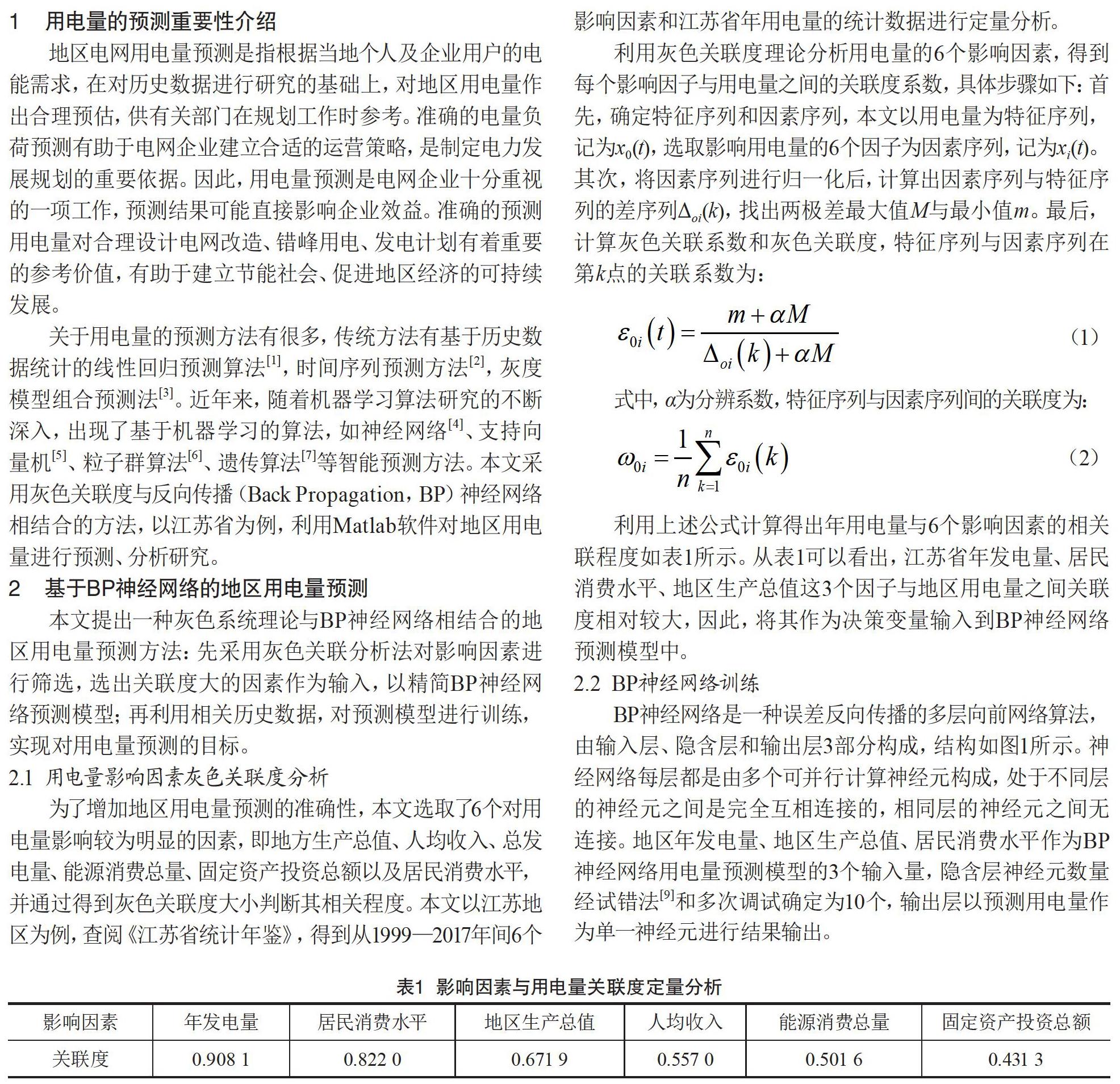
BP神经网络是一种误差反向传播的多层向前网络算法,由输入层、隐含层和输出层3部分构成,结构如图1所示。神经网络每层都是由多个可并行计算神经元构成,处于不同层的神经元之间是完全互相连接的,相同层的神经元之间无连接。地区年发电量、地区生产总值、居民消费水平作为BP神经网络用电量预测模型的3个输入量,隐含层神经元数量经试错法[9]和多次调试确定为10个,输出层以预测用电量作为单一神经元进行结果输出。
对神经网络进行训练是由已知样本求得网络的连接权值与阈值的过程,其主要思想是:首先,进行网络初始化,给各权值和阈值分別赋予一个区间(-1,1)内的随机数,设定误差函数,给定计算精度值和最大学习次数。其次,对于一组输入样本,通过BP神经网络计算隐藏层神经元的输入、输出和网络的实际输出。再次,计算误差函数对输出层、隐藏层各神经元的偏导数,将输出层的误差逆向传播至隐藏层,根据隐藏岑神经元误差更新网络权值和阈值。最后,计算全局误差,判断网络是否达到精度要求,当误差达到预设精度或学习次数大于设定的最大次数,则结束算法。
3 实验与预测结果分析
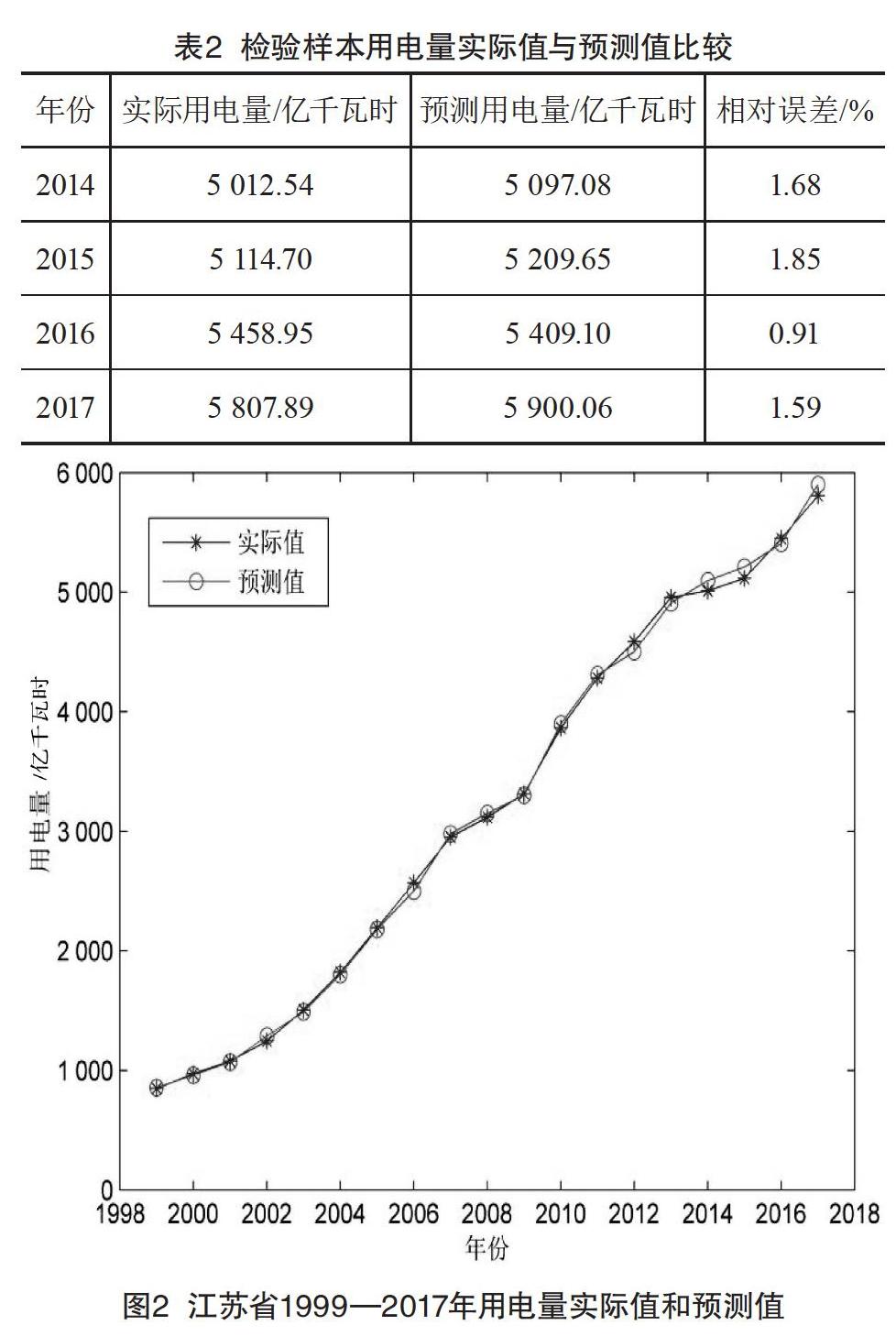
进行神经网络训练时,将江苏地区1999—2017年的用电量样本集分为训练样本和检验样本两部分,其中,抽取1999—2013年14组作为训练样本,2014—2017年4组数据作为检验样本。隐含层传递函数设定为logsig,输出层传递函数选定为tandig,训练函数为trainlm,学习函数 选用learngdm,网络的性能函数为MSE[11]。各参数选取分别为:学习速率0.005,期望误差0.000 01,最大学习次数1 000。模型经过训练之后,利用检验样本测试并验证其准确性和泛化能力,得到如表2所示的实际值与预测值对比结果。江苏地区年用电量实际值与预测值对比如图2所示。从预测数据与实际数据的对比来看,该BP神经网络预测模型性能较好,相对误差较小,完全能够满足决策的需求。
4 结语
本文采用BP神经网络技术,设计能够预测地区用电量的数学模型。由于影响居民和企业用电量的因素较多,采用灰色理论模型研究年用电量与影响因素之间的关联程度,进而选取3个相关性较高的影响因子,提高预测模型的精度和可操作性。BP神经网络用电量预测模型利用误差反馈修正参数,经验算该模型的预测结果和真实值之间具有较小的相对误差和平均相对误差,可以较为准确地预测出用电量,具有预测精度高,方法简单的优点。
[参考文献]
[1]李昉,罗汉武.基于多元线性回归理论的河南省用电量预测[J].电网技术,2008(S1):129-131.
[2]肖正,朱家明,祁孟阳,等.居民用电量的ARIMA时间序列预测[J].河南工程学院学报(自然科学版),2017(1):48-52.
[3]余健明,燕飞,杨文宇,等.中长期电力负荷的变权灰色组合预测模型[J].电网技术,2005(17):26-29.
[4]徐尧强,方乐恒,赵冬华,等.基于LSTM神经网络的用电量预测[J].贵州电力技术,2017(8):25-29.
[5]潘峰,程浩忠,杨镜非,等.基于支持向量机的电力系统短期负荷预测[J].电网技术,2004(21):39-42.
[6]沈建新,杨善林.智能电网视角下粒子群优化支持向量机的用电量预测[J].科技管理研究,2013(11):235-238.
[7]薛必克,李陈龙,郑亚先,等.遗传算法在中长期电量最优组合预测中的应用[J].华东电力,2012(9):1525-1527.
[8]曾波,刘思峰.基于灰色关联度的小样本预测模型[J].统计与信息论坛,2009(12):22-26.
[9]沈花玉,王兆霞,高成耀,等.BP神经网络隐含层单元数的确定[J].天津理工大学学报,2008(5):13-15.
