一种求解DGA图中具有长度约束的简单路径问题算法

何建军

摘要：具有长度约束的简单路径问题具有较高的应用价值。在一般图中，它是一个NP完全问题，除非NP=P，否則没有多项式时间算法。而对于一些特殊的图，如有向无环图，可以找到多项式时间算法。因此对有向无环图中具有长度约束的简单路径问题进行研究。首先根据有向无环图的特点，建立递归方程，然后根据递归方程给出一个在有向无环图中求解具有长度约束的简单路径问题算法，同时给出一个有向无环图中具有长度约束的简单路径构造算法。为证明算法正确性，进行相应实例验证，把求解该问题的时间复杂度由O（NxTxL）改进为O（（N+|E|）L），空间复杂度改进为O（[EI+N）。

关键词：有向无环图;简单路径;长度约束

DOI：10.11907/rjdk.182897开放科学（资源服务）标识码（OSID）：中图分类号：TP312文献标识码：A 文章编号：1672-7800（2019）010-0082-04

0引言

在图论中，k-path问题指在给定的图中找出一条长度为k的简单路径，是最长路径问题和最短路径问题的一种特殊情况。k-path问题在生物信息学、交通运输、数据挖掘和模式匹配等领域有重要的应用价值。具有长度约束的简单路径（Simple Paths with Length Constraint，SPLC）问题是k-path问题的推广，在一般图中求解SPLC问题是一个NP完全问题，求解难度很大，除非NP=P，否则没有多项式时间算法。但对一些特殊图，比如有向无环图、树，则存在多项时间算法。

有向无环图具有长度约束的简单路径问题（SPLCin DAGs），在序列模式挖掘、模式匹配、图的可达查询、多星成像等方面应用广泛。文献[16]把有向无环图中具有长度约束的简单路径问题应用于图的k步可达查询中。文献[18]把有向无环图中具有长度约束的简单路径问题应用于多星成像的圈调度中。Zhang提出了具有周期间隙约束的序列模式挖掘问题，并将该模式挖掘方法应用在DNA序列挖掘中;Tanbeer等将具有周期间隙约束的序列模式挖掘方法应用于购买模式的挖掘。尽管Zhang等采用空间变换的方法进行序列模式挖掘，但是该方法的基础是具有间隙约束的模式匹配问题。文献[21]研究了具有间隙约束和一次性条件模式匹配问题的求解方法，给出了将具有间隙约束的模式匹配问题转换为有向无环图的算法，使具有间隙约束的模式匹配问题与SPLC in DAGs问题建立了实质性联系。文献[22]把有向无环图中具有长度约束的简单路径问题应用于产品族零部件关系网络，并提出时间复杂度为O（N⁴）的算法。

有向无环图有很多特殊的性质，使一些在其它图上没有多项式时间算法的问题（除非NP=P），出现在有向无环图上。比如最长路径问题，在有向无环图中，可以用拓扑排序的方式求解。文献[8]利用网树这种特殊的数据结构给出在有向无环图上求解有长度约束的简单路径问题的一个多项式时间算法。本文利用有向无环图的有向、无环特性建立递归方程，设置边界条件，提出一种更简洁的动态规划算法。

1问题定义

定义1：图G=（V，E），其中V称为顶点集，E称为边集。从顶点u到v的路径是有序定点序列s={u=v₀，v₁，……，v_m=V}，其中定点序列应满足j-1，v_j>∈E（1≤j≤m））如果序列S中任何两个定点不重复出现，则称改路径为简单路径。路径长度是路径终边的数目。若i，v_j>∈E，则称v_i为v_j的前驱，v_j为v_i的后继。

定义2：具有长度约束的简单路径SPLC问题指给定图G=（V，E）中任意两点u，v∈V和正整数m，求解从u到v路径长度为m的简单路径数目。SPLC in DAGs指在给定的有向无环图中求解SPLC问题。

记有向无环图G的节点数为N，边数为|E|，长度约束为L，从v_i到v_j的长度为m的所有有向路径构成的集合S[i，j，m]，从v_i到v_j的长度为m且v_j的前驱为v_k的所有有向路径构成的集合S[i，k，j，m]。

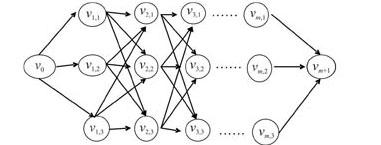
SPLC in DAGs问题的求解难度在于定点u和v之间的路径数有可能呈现指数形式，如图1所示，因此不能采用穷举法列出所有可能的路径并判定路径长度是否满足约束条件进行求解。本文采动态规划法进行求解。

2 动态规划算法

2.1递推方程建立

有向无环图性质包括：①若存在从v_i到v_j的有向边，则从任意一个顶点到v_i的有向路上，一定不会出现v_j，否则会形成一个圈;②若有向无环图任意一条有向路中均无重复的顶点，则为有向路径;③在集合S[i，k，m-1]和集合S[i，k，j，m]之间存在一一对应关系，即在有向五环图G中从v_i到v_k的长度为m-1的所有有向路构成的集合，和在有向无环图G中从v_i到v_j的长度为m且v_j的直接前驱为v_k的所有有向路构成的集合之间存在一一对应关系，这是因为从S[i，k，m-1]任取一条从v_i到v_k且长度为m-1的有向路p，添加上有向边k，v_j>后会构成一条从v_i到v_j、长度为m且v_j前驱为v_k的有向路，应用该方法从S[i，k，m-1]取得的任意两条不同的从v_i到v_k、长度为m-1的有向路，得到从v_i到v_j的长度为m且前驱为v_k的有向路不同。同样道理从S[i，k，j，m]任取一条从v_i到v_j、长度为m且v_j的直接前驱为v_k的有向路p′，吧有向边[v_k，v_j]去掉后悔得到一条从v_i到 v_k、长度为m-1的有向路，而且应用该方法从S_{i，k，j，m}取得任意两条不同的有向路，得到从v_i到v_k、长度为m-1的有向路也不相同。

2.2求解算法QNSPCINDGA

变量说明：A[N][L]是一个二维数组，S[j][h]存储的是从结点v_i到结点v_j且长度为h的路径数目。N是图G的结点数，L是设定的路径长度。A[N]是一个数组的，A[k]是一个集合形变量，其中春初的是以vk为弧头的所有弧的弧尾结点。Level记录当前正在计算的路径长度。

2.3从原点到其他结点的长路径构造

3算法QNSPCINDGA实例

4算法复杂性分析与比较

算法QNSPCINDGA初始化时取结点集的时间为O（N），读取弧集并初始化数组A的时间为。O（|E|），初始化M数组的时间为O（NL）。总共执行L次循环，而每次循环访问每个结点一次，访问每个结点时，访问其每条人弧1次，执行循环时间为O（（N+|E|）L）。所以算法时间复杂度均为O（（N+|E|）L）。算法QNSPCINDGA空间消耗主要在对图G的存储和S数组上。对图G的存储由A数组完成，而A数组中的每个元素是一个逆领接链表，每条人弧仅存储一次，且每个结点仅存储一次，所以对图G的存储空间为O（N+0E0）。数组S存储空间为O（NL），算法空间复杂度为O（|E|+NL）。

算法PA7HSPCINDAG的时间复杂度和空间复杂度估计：设从源点到其它节点结点且长度为L的路径地数目为W，输出每条长度为L的路径耗时最多为O（L），所以总时间复杂度为O（WL）。算法PATHSPCINDAG仅需要NL的二维数组S存储路径数目和进行L次递归调用，其递归调用栈深度为L，所以其空间复杂度为O（NL+L）。

5结语

本文对有向无环图具有长度约束的简单路径SPLC问题进行研究，针对有向无环图的特点提出了一个动态规划算法，并证明了算法正确性和有效性。该算法简洁明了，时间复杂度和空间复杂度均相对较低，避免了文献[8]的组合爆炸问题。边带权有向无环图中具有长度约束的简单路径问题是下一步研究对象。