城市需水预测算法比较

聂红梅 赵建军 李兴菊 王迎

摘要：建立高精度水量预测算法模型，有利于水资源充分利用。以北京市2002-2015年需水量为例，对数据进行相关性分析后选出主要影响因素，然后采用主成分回归法、逐步回归法、灰色模型以及BP神经网络共4种方法进行建模，并用北京市2016年和2017年数据进行模型精度验证。结果表明：4种方法都适合用于城市需水量预测，其中主成分分析和逐步回归分析两种方法主要考虑了多元线性回归存在多重共线性，但是逐步回归模型优于主成分回归模型。将4种模型进行对比验证，BP神经网络模型预测精度最高，平均相对误差达到0.79%，用来预测2016-2017年需水量，预测结果分别为38.66亿m³、39.49亿m³，适合作为城市需水量预测方法。

关键词：需水量预测;多重共线性;主成分回归模型;逐步回归模型;灰色模型;BP神经网络模型

DOI：10.11907/rjdk.191311开放科学（资源服务）标识码（OSID）：

中图分类号：TP312文献标识码：A 文章编号：1672-7800（2019）010-0069-05

0引言

水是不可缺少的資源，随着社会发展，需水量越来越大。为了最大限度减少水资源浪费情况，减少供水设施的各项投资总额，保证水资源供需平衡，对城市需水量进行准确预测是一种不错选择。目前，在城市需水量预测方面，国内外已有许多专家学者做了大量研究。如Brekke等在城市需水量预测中引入逐步回归法，该模型建模时间短且效率高;Jain等分别对8种模型进行评价，对短期用水进行预测、测试和检验;张洪国等用灰色预测模型建立年用水量预测模型，虽然预测精确度较高、易于检验，但是预测时间短;赵明等应用支持向量机模型，通过拉格朗日对偶形成凸函数，并优化求解，支持向量机模型降低了算法复杂度，提高了模型泛化能力，但要求数据量大。

总的来说，现有预测方法大体分为3类：定性预测法、定量预测法以及其它预测法。当掌握的历史资料比较缺乏时，可以用定性预测方法;当历史数据比较多且易于获得时，可以用定量预测法;其它预测方法包括类比法、指标分析法等。由于需水预测算法各有优劣，而进行需水预测时需结合预测目的、特点、用水变化规律等合理选择一种或几种预测算法，因此在进行水量预测时必然会面临预测算法的选择问题。

为了找到一种预测精度较高的城市需水量预测算法模型，本文分别采用多元线性回归中的主成分回归和逐步回归分析法、灰色预测模型以及BP神经网络算法预测城市需水量。尽管这几种算法在城市需水预测中已经有了一定研究，但是几种算法应用的比较分析相对不足。基于以上方法，以北京市2002-2017年需水量数据为例，对几种算法进行建模仿真并验证，找出其适应特性，为以后选择城市需水量预测算法提供参考。

1需水量预测方法原理

1.1多元线性回归模型

多元线性回归法是研究某个事物与其它多个变量之间关系的方法。其回归模型为：

1.1.1主成分分析

主成分分析法采用对数据从高维降到低维的方式选出几个不具有相关关系的综合指标，将几个综合指标作为主成分，建立它与因变量的回归方程，其中，几个主成分包含原始数据的大部分信息。主成分分析法一方面可以用来消除多重共线性和将m维降至p维（m>p），另一方面有时会出现命名不清晰的情况，无法解释其中一些变量，使结果不合理。

主成分分析步骤：

（1）数据标准化处理。表达式为：

1.1.2逐步回归分析

逐步回归分析通常用来消除共线性，通过选取最好的子集变量排除不显著变量，使得多重共线性被消除，从而使模型性能更佳。详细步骤是：从原始自变量中随意挑选一个变量开始，每个步骤中只引入或排除一个自变量，自变量是否引入或排除主要根据F检验与偏回归平方和加以判断。每次引入一个变量时，如果原来引入的变量由于新引入变量而使F变得不再显著，则排除该变量。每次引入或排除变量都要执行F检验，以保证每引入或排除变量前，回归方程中只有显著变量。不断重复这个过程，等到没有不显著的变量被选人回归方程，也没有显著变量被回归方程排除就结束。逐步回归分析法一方面可以保留显著变量和消除共线性，另一方面也容易将一些较重要的变量排除在外，导致信息不完整。

1.2灰色模型

灰色G（1，1）模型先对原数据序列进行一步步累加，生成趋势较大的新数据序列，然后利用新数据建模并预测，最后通过累减方式还原成原来的数据序列。根据灰色理论建立一元微分方程G（1，1）。

1.3BP神经网络模型

BP神经网络采用误差反向传播算法进行训练，且自学习能力、容错能力较强。其结构如图1所示。

BP神经网络包括正向传播和误差逆向传播。当进行正向传播时，输入信号经过隐含层处理后，转向输出节点以通过某种变换产生输出信号，然后计算输出误差;若实际输出值与期望输出值没有达到所需要求，则进行误差逆向传播。误差逆向传播对误差按照原来通路返回的方式，通过修改连接权和阈值，使误差沿目标的负梯度方向调整。不断重复这一迭代过程，直到达到一定条件，训练即可停止。其网络训练过程为：①网络初始化;②计算隐含层的输出;③计算输出层的输出;④计算误差;⑤更新连接权;⑥更新阈值;⑦判断是否达到停止条件，若没有，则返回过程②继续循环，反之，结束训练。

2应用实例

2.1数据处理

收集整理2002-2017年北京市需水量相关数据。考虑经济、社会、气候是影响城市总需水量的主要因素，选取北京市11个影响因子为主要影响因素。如表2所示，x₁表示常住人口（万人）、x₂表示人均可支配收入（元）、x₃表示人均生产总值（元/人）、x₄表示工业生产总值（亿元）、x₅表示社会固定资产投资（亿元）、x₆表示城市绿化覆盖率（%）、x₇表示有效灌溉面积（千hm²）、x₈表示农作物播种面积（万hm²）、x₉表示发电量（亿kw.h）、x₁₀表示年降水量（mm）、x₁₁表示平均气温（℃），需水量（亿m²）用y表示。

应用SPSS软件对影响因子进行相关性分析，选择相关性系数|r|>0.7的影响因子，即人口、人均可支配收入、人均生产总值、工业生产总值、社会固定资产投资、城市绿化覆盖率、农作物播种量以及发电量作为主要影响因子。

2.2多元线性回归模型预测结果

判断8个主要影响因素是否存在多重共线性情况，结果如表3所示。

通过表3可知，其容差范围在0.001～0.010之间，均小于0.1;方差膨胀因子范围在52.278-918.564之间，均大于10，由此可以判断自变量间有很强的共线性情况。下文分别采用主成分分析和逐步回归分析解决该种情况。

2.3灰色预测模型预测结果

采用北京市2002-2015年用水量數据建立灰色G（1，1）模型，预测2016-2017年用水量。先用灰色模型中的式（7）求出参数a，再把a代人式（5）求出参数u，然后把a和u两个参数代人式（9），从而求出预测值，模型验证采用后验差检验法。最终得到的灰色预测模型如下：

其中，均方差比值和小误差概率分别为C=0.343 1、P：0.857 1;参照预测精度等级表，可以得出其预测精度等级为合格。由此可以说明灰色G（1，1）模型适合用于城市需水量预测。

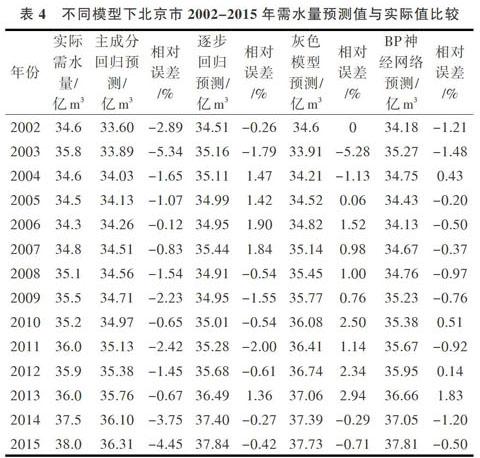
利用该模型预测北京市2002-2015年需水量，结果如表4所示。

2.4BP神经网络模型预测结果

利用北京市2002-2015年需水量相关数据，把经过皮尔逊相关性分析后得到的8个主要影响因子作为输入、实际需水量作为输出，建立BP神经网络。BP神经网络主要采用学习率自适应梯度下降法，迭代次数设置为100次，误差目标值和学习速率分别设置为0.001、0.000 5;经过不断训练后得到最终的神经网络模型。用该模型预测2002-2015年需水量，最终得到不同模型下北京市2002-2015年实际值与预测值及相对误差（见表4）。

通过分析表4，比较这几种算法模型结果可得：主成分回归模型和逐步回归模型的平均相对误差分别为2.07%、1.14%;灰色G（1，1）模型比逐步回归模型的平均相对误差高0.33%，且2002年预测值与真实值一致;而利用BP神经网络模型预測时，平均相对误差为0.79%，在2004-2007年连续4年中相对误差都低于平均相对误差，总体拟合效果较好。综合可知，上述模型中主成分回归模型精确度最差，灰色模型精确度次之，逐步回归模型精确度稍高，而BP神经网络模型精确度最高。

为了进一步验证模型精确度，将上述4种模型用来预测北京市2016-2017年用水量，该两年实际值分别为39.0亿m³、39.5亿m³。利用主成分回归模型得到的预测值分别为36.54亿m³、36.67亿m³;利用逐步回归模型得到的预测值分别为38.29亿m³、38.89亿m³;利用灰色模型得到的预测值分别为38.06亿m³、38.40亿m³;而利用BP神经网络得到的预测值分别为38.66亿m³、39.49亿m³。综上可知，BP神经模型得到的预测值更符合实际值，相对误差分别为0.88%、0.03%，具有更高精确度，可以用来预测城市需水量。

3结语

在多元线性回归中，采用主成分分析和逐步回归分析两种方法都是为了消除多重共线性，但是应用在城市需水量预测中时，逐步回归模型的预测精确度明显更高。灰色G（1，1）模型与逐步回归模型的预测精度相差不大，而灰色G（1，1）与BP神经网络模型的预测精度相比差距较大。主要原因是：一方面，灰色G（1，1）模型的精确度要求累加数据具有指数性质，而实际累加的数据未必具有指数规律;另一方面，灰色G（1，1）模型没有考虑其它影响因素，因此导致预测结果与实际值相比存在较大误差。BP神经网络模型不仅考虑需水量相关影响因素，而且建模时把全部数据同时作为训练数据和验证数据，通过不断训练和检验，很大程度上提升了模型预测精度，使得最终预测精度为0.79%。在实际生活中，城市需水量预测有多种方法。当有大量历史数据时，可以考虑灰色模型和BP神经网络;若考虑城市需水量各种影响因素且数据容易获得时，可采用BP神经网络及逐步回归分析算法。