基于边界层理论的低渗透油藏非线性渗流新模型

张世明

（中国石化胜利油田分公司勘探开发研究院，山东东营 257015）

目前，低渗透油藏已成为胜利油田增储上产的重要阵地，明确低渗透油藏的渗流机理和研发适用于低渗透油藏的数值模拟软件对低渗透油藏高效开发具有重要意义［1-2］。低渗透油藏定义为储层平均渗透率小于50 mD 的油藏［3］。岩心驱替实验和开发实践表明，相比于中、高渗透油藏，低渗透油藏具有更细、更小的孔喉［4］，油水在低渗透油藏中的渗流不再符合传统的达西定律，表现为明显的非线性渗流特征，同时存在一定的启动压力梯度［5-9］。

前人对低渗透油藏的启动压力开展了一系列研究［10-13］，建立了考虑拟启动压力梯度的非达西渗流理论。但随着低渗透油藏及致密油藏的开发，实验研究成果、数值模拟技术成果和矿场实践表明，低渗透油藏和致密油藏仅在近井区域存在拟线性渗流，在油藏范围内的渗流主要以非线性形式存在［14］。而拟启动压力梯度理论以门槛值的形式将低速流动区近似为不流动区，忽略了低渗透油藏低速流动区对开发效果的影响，对于低渗透甚至致密油藏，计算误差大，不能精确地描述其渗流特征。为弥补拟启动压力梯度模型在渗流规律描述中存在的缺陷，针对低渗透油藏非线性规律开展大量的实验研究和理论分析，并建立一系列低渗透油藏非线性渗流模型。黄延章建立了分段的低渗透油藏非线性渗流模型［15］，时宇等开展流体在毛细管中渗流规律的实验研究，分析了毛细管中的边界层厚度变化规律［16-17］。姜瑞忠等基于边界层理论和毛细管模型建立了多参数的连续型非线性渗流模型［18］；SONG Fuquan等分析了在毛细管中具有负滑移的流体边界特征，推导出牛顿型流体的低渗透油藏非线性渗流模型［19］；苏海波分析了低渗透油藏中宾汉姆流体的渗流特征，基于边界层理论建立动态启动压力梯度模型和连续型的低渗透油藏非线性渗流模型［20］。

在低渗透油藏非线性渗流模拟器研发方面，目前的商业化油藏数值模拟器是以线性达西渗流规律为基础开发的，不能准确描述低渗透油藏开发中存在的非线性流动特征。近几年研制的仅考虑基于低渗透拟启动压力梯度模型建立的低渗透油藏非达西渗流数值模拟技术，降低了流体在低渗透油藏中的渗流能力。在油藏开发的井网井距的优化设计过程中应用以上2种油藏数值模拟技术致使预测结果存在较大的误差。因此，需要对低渗透油藏渗流规律进行研究，建立能够准确描述低渗透油藏的非线性渗流特征的描述模型，开发适应于低渗透油藏的非线性渗流数值模拟软件，为低渗透油藏的高效开发提供技术支持。

1 低渗透油藏非线性渗流机理

由于低渗透油藏复杂的孔喉结构特征、特殊的流体性质及地层油与孔隙壁面间强烈相互作用，使得流体在低渗透油藏中的渗流特征不再符合传统的达西渗流规律，表现为明显的非线性渗流特征，同时具有一定的启动压力梯度。

1.1 低渗透油藏非线性渗流特征

单相流体在低渗透油藏中的流动呈现为非达西渗流的事实已得到大量学者的证实。由典型的低渗透油藏非线性渗流曲线［21-22］（图1）可见，流体的渗流速度与驱替压力梯度的关系不再遵循传统的达西定律，初期表现为非线性渗流特征，后期呈线性渗流特征。当驱替压力梯度小于A时，体系内未产生流动；当驱替压力梯度达到A时，流体开始流动；当驱替压力梯度大于A且小于B时，流体呈现非线性流动；当驱替压力梯度大于B时，流体呈现达西流动；将呈线性渗流时的直线段反向延长，与横坐标轴相交于C点，可得到拟启动压力梯度。

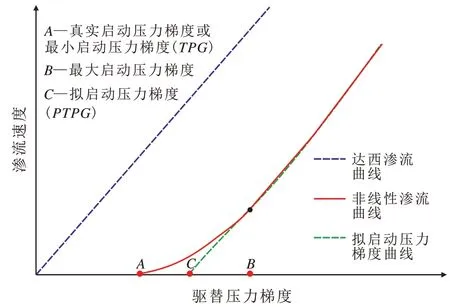
图1 典型低渗透油藏非线性渗流曲线示意Fig.1 Schematic diagram of typical nonlinear percolation curve in low-permeability reservoir

针对低渗透油藏中流体的复杂渗流特征，黄延章首先提出渗流流体的概念［3，15］，指出吸附在多孔介质孔隙壁面的边界流体是由固液相互作用力造成的，受微纳米尺度效应的影响而不发生流动，且边界流体层厚度与流体的组成和多孔介质的性质有关。微管流动实验［16-17］及分子动力学模拟［23-24］证明，微纳米尺度下微管壁面存在不流动边界层，厚度随驱替压力梯度增大而减小。

当地层油在低渗透多孔介质中渗流时，吸附在孔隙内壁表面上的原油形成具有较高黏度和极限剪切应力的边界层。当驱替压力梯度克服了具有最大半径的喉部边界层的剪切应力时，才允许流体通过喉道进入渗流空间。该驱替压力梯度被定义为最小启动压力梯度，且随着驱替压力梯度的增加，边界层的厚度减小；随着驱替压力梯度的进一步增加，储层中半径较小的孔隙和喉道中的流体开始流动，致使参与流动的喉道数量增加，在渗流曲线上表现为驱替压力梯度与流速呈非线性关系；当驱替压力梯度增加到最大启动压力梯度时，原油边界层的厚度不再随驱替压力梯度的增加而变化，此时，流速和驱替压力梯度间表现为线性关系。

1.2 地层油边界层厚度特征

应用恒速压汞实验方法测得不同岩心的孔喉半径，利用岩心流动实验［25］测试储层液膜的厚度。研究结果（图2）表明:胜利油区低渗透油藏孔喉细小，平均孔喉半径为0.2～2 μm，地层油的边界层厚度为0.2～0.8 μm，边界层厚度与孔喉半径相近，处于同一个数量级。因此，胜利油区低渗透油藏的边界层效应对渗流特征的影响不可忽视；而中、高渗透储层孔喉半径与边界层厚度差异大，边界层厚度相对孔喉半径比值小，边界层效应对中、高渗透油藏中的流体渗流特征的影响可以忽略不计。

2 低渗透油藏非线性渗流模型的建立

2.1 单个毛细管的流量模型

在低渗透多孔介质中，孔喉半径与边界层厚度处于同一个数量级上，流体与多孔介质内表面间的相互作用强烈，影响了流体通过低渗透多孔介质的渗流特征。毛细管（半径为2.5 μm）中去离子水驱替实验结果［17］表明:驱替压力梯度越大，边界层厚度越薄，边界层厚度与毛细管半径比值越小，即边界层厚度随驱动力的增大而减小，呈现指数衰减的规律（图3）。

图2 不同空气渗透率岩心孔喉半径及边界层厚度分布Fig.2 Distribution of pore radius，throat radius，and boundary-layer thickness of cores with different permeability

图3 驱替压力梯度与边界层厚度和毛细管半径比值的关系Fig.3 Exponential relationship between displacement pressure gradient and ratio of boundarylayer thickness and capillary radius

由此推测，当驱替压力趋近于0时，可以把整个毛细管内流体视为边界层，即边界层厚度等于毛细管半径。根据上述研究成果，假设边界层厚度与驱替压力梯度的变化关系为:

低渗透油藏的孔隙及喉道半径细小，流体通过喉道时表现为牛顿流体的流动特征。牛顿流体的应力本构方程［24］为:

假设一根半径为r0的毛细管，（2）式可描述为:

假设边界层厚度为δ，相当于有效流动半径减小δ，对（3）式从0到r0-δ进行积分:

则得到牛顿流体沿半径方向的速度分布为:

将（1）式代入（5）式，并在整个过流断面上积分，得到驱替压力梯度作用下的单个毛细管的流量公式为:

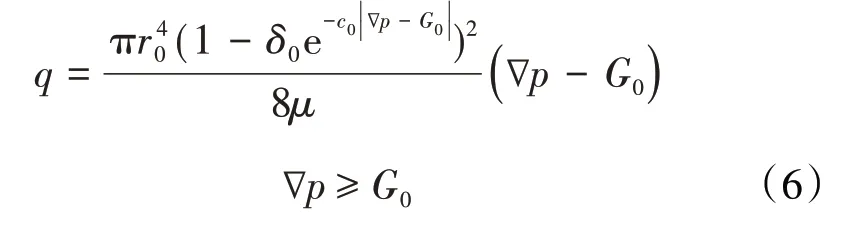
2.2 低渗透多孔介质非线性渗流模型

利用毛管束模型［26］可以得到低渗透多孔介质中的渗流模型，假设多孔介质是由N根不等径的毛细管组成，则多孔介质的流量公式为:

可得低渗透油藏的渗流公式为:

（9）式中，当δφ=0，G=0 时，（9）式即为传统的达西渗流模型。因此，传统的达西渗流模型是本文建立的低渗透油藏非线性渗流模型的一种特殊形式。

为了分析（9）式的物理含义，考虑一维低渗透油藏中的流体流动，假设油藏过流面积为0.002 m2，渗透率为1 mD，地下原油黏度为2 mPa·s，由（9）式可以计算原油流量随压力梯度的变化，从不同的非线性渗流系数下的驱替压力梯度与流速的关系（图4）可以看出，当cφ值较大时（cφ为1.50×10-6m/Pa），流动特征接近于达西渗流的线性流动；当cφ值较小时（cφ为0.05×10-6m/Pa），可以明显地看到压力梯度小的条件下，流量减小，偏离达西渗流；当cφ趋于无穷大时，（9）式为达西方程。由此说明，该模型能够较好地描述流体通过低渗透多孔介质中的渗流特征。

图4 低渗透多孔介质中驱替压力梯度与流速的关系Fig.4 Relationship between displacement pressure gradient and flow velocity in low-permeability porous media

3 模型的验证与应用

为了检验模型的适用性，选择低渗透岩心进行室内渗流实验，并用（9）式对实验结果进行拟合。岩心PGL-135 的渗透率为1 mD，流体黏度为1.1 mPa·s的条件下，由渗流实验和拟合结果（图5）可以看出，基于边界层理论的渗流模型能较好地描述低渗透油藏的非线性渗流现象。

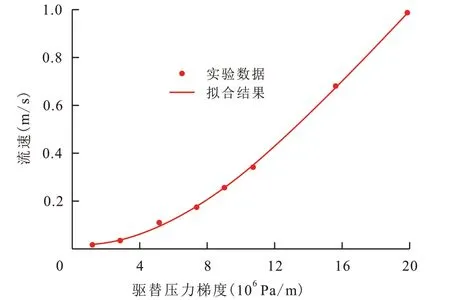
图5 低渗透岩心中驱替压力梯度与流速的实验和拟合结果对比Fig.5 Comparison between matching data and experiment results of displacement pressure gradient and flow velocity in low permeability core

基于岩心PGL-135 的测试数据，应用所建立的非线性渗流模型，计算油藏单井径向流动条件下的压力场分布（图6）。从图6中可以看出，受边界层效应影响，油藏区域可划分为3 个流动区:易流区、缓流区和滞留区。研究分析表明，易流区驱替压力梯度大，流体易于流动，累积产量贡献率高达约95%；缓流区驱替压力梯度小，流体难以流动，累积产量贡献率小于5%。缓流区和易流区较好地反映了从油层供油边界到油井井底之间，随着驱替压力梯度由低到高，储层流体由非线性流动向线性流动的变化。相比于整个径向泄油区，易流区半径占比为70%，面积占比为49%；缓流区半径占比为30%，面积占比为51%。因此，对于低渗透油藏，其有效的泄油半径近似等于易流区半径，合理的井距优化应以易流区半径为主要依据，而不是缓流区外边界对应的最大泄油半径。据此，绘制了缓流区半径与泄油半径比值与空气渗透率的关系曲线（图7）。从图7 中可以看出，低渗透油藏的储层渗透率越低，缓流区半径占比越大，易流区边界与缓流区边界间距差异越大。

图6 低渗透油藏单井径向渗流模式Fig.6 Radial percolation mode of single well in low permeability reservoirs

图7 缓流区半径与泄油半径比值和空气渗透率的关系Fig.7 Relationship between air permeability and ratio of radius of slowly flow area to drainage radius

因此，基于不同渗透率条件下易流区和缓流区的差异性特征，探索差异化开发对策，增大有效驱替压力梯度、扩大油藏波及系数，提高低渗透油藏采收率，是实现低渗透油藏有效开发的重要途径。一般低渗透油藏缓流区较小，易流区、缓流区边界接近，可利用拟启动压力梯度模型计算泄油半径，开发上可以通过井网适配建立有效驱替压力梯度，促使注采井间缓流区（或易流区）边界对接，提高油藏波及系数。特低渗透油藏缓流区大，非线性渗流对开发效果影响较大，须采用非线性渗流模型准确描述渗流规律，指导油藏开发方案设计；可考虑通过储层改造（如直井长缝定向压裂等）来改变注采井间流线，变径向流为平行流，促使缓流变易流，提高有效驱替压力梯度；致密油藏缓流区最大，可通过有效泄油半径优化合理井距，确保井间易流区边界对接，减少死油区，提高油藏储量动用程度。

4 结论

低渗透油藏由于孔隙结构复杂、流体性质的特殊性及流体与孔隙内壁间的强烈相互作用，使得流体在低渗透油藏中的流动呈现出非线性渗流特征。胜利油田低渗透油藏的流体边界层厚度与孔喉半径处于同一个数量级，边界层效应是低渗透油藏产生非线性渗流的根本原因，中、高渗透油藏边界层厚度相对小，非线性渗流特征不明显。

针对胜利油区低渗透油藏的非线性渗流特征，基于流体的边界层理论，提出了低渗透油藏非线性渗流模型，该模型能够完整地描述从非线性渗流到线性渗流的全部渗流过程，准确表征非线性渗流特征。利用非线性渗流理论，建立单井径向渗流模式，将单井渗流划分为易流区、缓流区和滞留区。不同类型低渗透油藏，易流区边界与缓流区边界之间的差距是不同的，提高采收率的技术不同，渗透率越低，易流区、缓流区边界间的差距越大，非线性渗流特征对开发效果影响越大。

符号解释

δ——边界层厚度，m；∇p——驱替压力梯度，Pa/m；r0——毛细管半径，m；δ0——静态边界层厚度，且0 ＜δ0＜1，无量纲；c0——非线性渗流系数，m/Pa；G0——流体通过半径为r0的毛细管时需要克服的最小启动压力梯度，Pa/m；τ——流体所受的切应力，Pa；μ——流体的黏度，Pa·s；γ˙——流体的应变，1/s；v→——流体渗流速度，m/s；r——流体通过毛细管的有效渗流半径，m，r=r0-δ；q——流体通过单个毛细管的流量，m3/s；Q——流体通过多孔介质时的流量，m3/s；N——毛细管总数，根；ni——半径为ri的毛细管总数，根；ri——第i个毛细管半径，m；δi——半径为ri的毛细管中最大边界层厚度，m；ci——半径为ri的毛细管中流体非线性渗流系数，m/Pa；Gi——流体通过半径为ri的毛细管时需要克服的最小启动压力梯度，Pa/m；A——多孔介质的渗流面积，m2；φ——多孔介质的孔隙度，无量纲；K0——多孔介质的绝对渗透率，1015mD；δφ——流体通过低渗透多孔介质时的静态边界层厚度，无量纲；cφ——流体通过多孔介质时的非线性渗流系数，m/Pa；G——流体通过多孔介质时需要克服的最小启动压力梯度，Pa/m；Rd——径向泄油区半径，m；Ref——易流区半径，m；Rsf——缓流区半径，m。