一种针对并行系统的状态存档冲突消减方法

苏 谟,赵玉彬,郭锐锋,王其乐

1(中国科学院大学,北京 100049)2(中国科学院 沈阳计算技术研究所,沈阳 110168)3(沈阳市第三十一中学,沈阳 110021)

1 引 言

随着摩尔定律的失效及三维可视化[1]需求与设计的复杂性日益加深,逻辑处理的并行化[2]越来越受到重视.同时随着Entity-Component-Entity[3-5]模型等面向数据设计方式的提出,逻辑的并行处理设计难度也越来越低.在虚拟仿真等三维可视化系统设计中,状态存档[6](存档回放)一直作为一个必需的功能存在,是后期复盘分析以及系统的缺陷分析等需求的核心组成部分.在并行设计的虚拟仿真系统的中,系统状态的变化需要满足实时性,但是由于状态改变的速率较快,需要存档的状态信息量较大,以及并行存档过程为了解决并行冲突,必须采用串行化处理方式等,导致了并行系统的存档过程延迟大等问题.而且,在并行逻辑处理的系统中,由于存在系统调度以及任务间交叉运行等动态情况,即使采用串行化的状态存档方式,也无法保证存档的状态是按照状态改变的时序记录下来的,会在存档过程中出现状态存档的顺序与实际状态发生的顺序不一致的情况.

针对并行系统中状态存档冲突的问题上,文献[7]在设计异构并行仿真引擎的过程中,解决存储冲突的方式是利用GPU的加法原子操作来设置同步点,多个线程在该点上顺序执行,这种方式原理上还是采用串行执行的方法解决冲突;文献[8]提出一种名为Instant Replay的存档重放方法,这种方法按照访问内存的顺序进行存档和设计回放,并且适用于并行系统,然而从内存访问层面设计状态存档会造成巨大的性能开销;文献[9]分析了存档回放设计的困难原因,并且说明了正确使用互斥、同步等操作可以提高程序的性能,但是会由于状态信息的数据量大而会造成很大的性能开销;文献[10]提出从效率方面对存档回放进行分析和评价;文献[11]分析了在状态存档和回放问题上的软件和硬件实现的接口.由于并行的三维可视化系统状态存档属于非严格确定性[10]的状态存档类别,保证可见状态相同即可,对于线程间执行期间的交叉顺序并不敏感,通过逻辑时钟来确状态改变的顺序是可以保证其正确性的.存档性能开销主要集中存档过程的串行化处理上,虽然无锁队列[12]的应用一定程度上改进了状态存档过程中性能上的问题,但是无锁队列本身设计较复杂并且在状态存档过程中会出现时序错乱的问题.因此,本文针对并行系统下状态存档以及时序上的问题,提出一种冲突消减的方法,减少并行存档过程中的冲突,并且在状态恢复时可以保证完整的时序,同时该方法具有简明和高效等特点.

2 并行系统下状态存档问题分析与解决

并行系统下的状态存档问题集中点在如何避免并行状态存档下串行化的执行问题,以及如何来满足严格的时序性问题上.并行系统下存档冲突的问题是难以避免的,但是通过一定的手段可以将发生冲突的概率降低.状态存档恢复过程的时序性是保证复原过程正确的关键,通过对于并行系统下状态存档的形式、目的进行分析,并且通过严格定义的方式,保证在复原过程中状态序列的时序性特征,正确还原出整个状态变化的过程.

2.1 并行状态存档中的原则与概念

在并行系统中状态的存档通常需要考虑的以下三个基本原则:

原则1.确定性:存档的状态数据作为输入时,保证逻辑计算对于相同输入获得相同的输出结果.针对于不确定的系统变量参与的计算,需要同时将这些系统外部参数作为确定性的状态进行存档,避免环境的不同而导致的计算结果的不同[13].

原则2.时序性:所有的状态信息具有在整个状态变化序列中对应的位置,从时序角度考虑为对应的状态改变的时间节点,即状态存档的状态信息在复原过程中需要满足其生成时的时序性.广义的方式是在存档时将状态打上逻辑时钟时间戳来表示时序,则复原时可以保证时序性,同时逻辑时钟需要满足稳定性、非递减性等特点.

原则3.无感知性:状态的存档过程应该尽量低延迟.状态存档不得影响到正常的逻辑推进,不得使得某个线程长时间阻塞,所以应该是低延迟和稳定延迟.

本文中包含的逻辑帧率与逻辑时钟的相关概念解释如下:

逻辑帧率:逻辑帧率为系统逻辑操作的处理频率,与渲染帧率分离,可表示三维可视化系统中状态更新的快慢.

逻辑时钟:表示三维可视化系统内部操作的时间基准.可以与系统时钟进行换算,并且通常是从零点开始计算.

2.2 并行系统状态存档问题分析

在并行系统状态存档过程中的性能和时序性上的问题,主要集中在状态信息添加的方式采用追加的形式,但是由于并行执行下很可能同时多个线程都需要进行状态信息添加,从而导致排队阻塞进而影响性能.虽然追加的方式在一定程度上满足时序性,但是由于系统调度等因素,即使是追加的方式同样也存在时序性不稳定的情况出现.

2.2.1 状态时序性问题分解

通常定义一个状态是否是同时发生,在不考虑偏序或全序的关系的条件的前提下,一般化的定义如公式(1)所示,这里同时发生的状态实际上指的是在一个小时间间隔内同时发生的状态改变.类比桶排序中的桶,这里引入时间桶的概念,将连续的时间离散成为一个个代表一段时间区间的紧密排列的时间桶,状态改变时间在一个相同桶区间内通常认为是同时发生的.

|Tp1-Tp2|≤ε

(1)

如公式(1)表示线程P1产生状态信息的时间和线程P2产生状态信息的时间小于给定的阈值ε.因为模拟仿真等并行系统下采用的是非严格确定性状态存档,只要处理时间在一定范围内我们可以认定两者是同时发生的.基于这个认识,在并行处理的情况下将同时改变的状态进行离散在不同的小时间片内,只要控制误差范围的精度,这种方式具有一定的可用性.并且在实际的情景下,线程的逻辑帧率处理是通过循环收集的方式,线程的执行实际上是收集上一个逻辑帧到当前逻辑帧时间区间det内的事件.例如Unity中针对输入的处理是在每个逻辑帧的某个阶段去处理.

(2)

如公式(2)det是两次逻辑帧的时间间隔,f代表px线程的第i个逻辑帧结束时间.计算在px线程在时间区间det范围内的所有的逻辑并更新状态,虽然通常认为状态改变是立即发生,实际上并不按照状态改变的时刻立即执行.本质上这里是允许有ε的误差的,所以假设将状态信息放入时间桶时,可以放在表示当前时间节点的时间桶前或者后距离ε/2的范围内的桶里.

2.2.2 针对严格时序性的改造

以上方式在某些情况下是可行的,比如逻辑时钟的粒度比较大时,但是实际环境下状态的存档由于并非是严格按照时序排列,而且通常ε的值较小,所以可以进行操纵的空间很小.在严格场景的情况下逻辑处理由于时间序的错乱会引发一定的问题.

针对以上的分析进行扩展,因为通常的状态存档操作是为了后期的复盘分析等使用,所以需要在分析和复原的过程中才要求严格的时序排列.实际一定范围内的存档序列不符合严格的状态时序序列,在恢复时采用批量加载的情形下,是可以不影响恢复过程的严格有序与时间复杂度的.由于严格的时序排列存档过程在并行执行下,必然会引发冲突而降低效率并且时序性也不能根本保证,所以为了提高效率降低延时,可以将整个状态存档信息按照状态生成时的序列设计为基本有序即可,允许在时间片段ε之内是无序的,并且保证时间片段ε的无序并不影响状态的恢复.这里的ε不再是之前的误差,而是人为设定的值,可以比误差大的多,即在这个范围内并不严格要求状态存档时完全按照状态改变时的时序排序.而且我们保证的这个局部的无序是向前的,即状态放置位置在时间桶中存放更靠前,这样的设计具有很好的性质可被利用.

图1 状态存档示例Fig.1 Status record example

如图1所示为一个人为设置的ε=3的误差范围的示例,第一行为逻辑时钟,时序性使用逻辑时钟来表示,逻辑时钟用来表示系统推进的速度以及状态发生的时间节点.逻辑时钟是均匀严格的递增序列,如果按照严格的时序状态信息存档,即传统的追加的方式应该是第三行的完全时间序列,但是这种方式在并行的情况下det范围内可能需要存档多个状态数据,而不是上面所列的一个状态数据,这样多个状态因为都要追加到最靠前的状态数据后面,会形成串行化的处理,必须等待同时间段的其他先提交的线程处理完才能轮到自己.第二行是非严格的状态存档顺序,并且ε=3,如图1时间戳为t的值,最终会落在状态区间[t-3,t]的范围内,如在t=6的时候的状态信息,实际上落在了t=4的位置,t=8的状态信息实际上落在了t=7的位置.这里的偏移不会超过ε,并且是完全向前偏移,例如时间t=5的状态信息不会出现在t>5的位置,也不会出现在t<5-ε的位置.所以当有一条状态数据的时候,我们获得当前的逻辑时钟并通过哈希函数把他放在之前的ε的位置区间内即可,由于这样的位置有多个,所以大幅度减少线程并行之间的冲突.

2.3 不严格时序方法的偏移ε分析

这里将存档问题进行抽象简化,将多线程并行的存档看做周期性循环的行为,每个周期都是M个进程同时存入状态数据,多个周期是相互独立的.由于ε个桶被访问到的概率相同,则对于单独一个桶中被线程并行访问数量X服从二项分布.

(3)

(4)

(5)

公式(3)中的P{X=k}代表一个桶中同时k个线程访问的概率,p代表一个线程落在某个桶中的概率,ε是线程可以存放的状态桶的数量,M是线程的数量.当X为0和1的时候我们认为没有出现碰撞,当k>1时代表发生了碰撞并且需要等待前面k-1个线程的完成,则某个桶中发生碰撞时需要等待的前面需要处理的线程的期望如公式(4)所示.通过组合数和二项分布概率计算化简得到在一个写入周期内,每个桶中出现等待线程数量的期望如公式(5)所示,其中E′代表一个桶中线程需要等待处理线程数量的期望.

E″=εE′

(6)

(7)

由于可以认为每个桶相互独立,则每个周期出现等待的期望通过期望公式计算得出结果为公式(6)所示,整理得到公式(7)所示,其中一个周期的总期望用E″表示.通过公式(7)的分析,在M确定的情况可以观察到随着ε的增大期望值在减少;在ε确定的情况,随着M的增加期望值在增大,由于M表示并行度,可以理解为固定值.实际上可以通过以上的计算获得理论上在并行状态存档的过程中的实际加速比如公式(8)所示.

(8)

通过公式(8)的计算我们可以得出通过M在执行写入需要等待的时间期望与加速比.以上的公式结果可以用来评估并行状态存档过程中等待时延、发生碰撞概率等情况,可用于调整初始参数.通过以上公式分析,在M确定的时候,当ε增大到一定范围,则E″趋近与0,例如当M=4,ε=100时E″=0.06,由此可知等待线程数量的期望值较小,即碰撞的线程数量很少.此时的状态存档过程的加速比是Sp≈4.

另外,当发生冲突的时候并不一定就需要一定放在某个桶里,这里只要求放在[T-ε,T]的范围内的桶里即可,所以可以放入桶有多个.当放入过程与其他的线程放入过程产生冲突是可以使用重哈希操作,再次进行哈希操作来找没有发生冲突的桶进行加入状态信息,这种方式极端情况下会出现“饿死”现象,不是延迟稳定的,所以本文主要针对冲突等待的情况.

2.4 不严格时序方法状态复原分析

在不严格时序方法状态复原的过程中,涉及到两个问题,分别是针对给定的一批数据,如何判断给定逻辑时钟区间内的状态数据被加载完成,以及如果对加载完成的状态数据进行排序处理.

问题1.给定一个如上文所提到的非严格时间递增的状态序列,根据前面的介绍这里可以认为理解为一个存在磁盘上的数据文件,从这个文件中批量加载数据,如何确定在[0,T]这段逻辑时钟区间内的状态已经完整被加载到内存中.

因为数据文件中的状态数据是乱序的,在正常情况下无法一次将整个数据文件全部加载到内存排序.需要判断加载到一定数据量之后,来确定[0,T]的时间段内的状态是否已经完整了,这个时候才可以执行到当前的逻辑时钟T,否则可能会出现状态丢失的情况.

针对这个问题,首先在状态复原过程中,发现时间戳是T的状态并不意味着[0,T]的区间内已经初始化完成,因为这条状态很有可能是前移的了.当批量文件中的状态数据时,发现加载的状态的时间戳t并且满足t>T+ε时,可以确定之前[0,T]区间所有状态数据已经就绪了.这里的采用贪心的方式进行证明:由于状态数据包含表示状态发生时的时间戳信息,当发现第一个时间戳大于等于T的状态数据,此时这个状态可能向前发生了偏移,而且最多前推ε个时间间隔,所以此时最多向后再推ε个逻辑时钟间隔,就可以保证T之前的数据完全加载到了,判断的依据就是出现了t>T+ε的状态.所以需要找到时间戳t>T+ε的记录,此时可以保证时间T之前的状态数据已经被完全加载.同理也可以推断如果通过批量加载最后的状态时间戳是T,则表示T-ε之前的状态已经加载完成.

问题2.如何将批量加载到内存的状态数据进行排序使其严格的按照逻辑时钟顺序递增.首先通过前面的分析,可以假定一定数量的状态数据已经存在于内存中了,现在需要对这些含有时间戳的状态数据进行排序.前面已经证明了在一段时间[0,T]如何确定是否已经数据加载完成.由于这里主要是一个局部是无序的而不是完全无序的,所以可以直接使用桶进行排序,每个状态都有时间戳信息所以在哪个桶代表的时间间隔里是确定了的,只要通过计算将其放在对应的桶中即可,这里可以假定有一个无限时长的分好时间桶的数据结构,只需要计算出每个状态在这个桶中的位置即可.这种方式的时间复杂度为对于每条状态所用的时间复杂度为O(1),所有状态恢复的时间复杂度与状态数量N成正比为O(N).综上,在复原过程主要步骤为:确定时间节点T、批量加载状态数据并进行桶排序.

3 状态存档与复原实现方法

本小节主要针对如上所提出的方法的基本思想的实现,主要包括状态磁盘存档以及状态如何从磁盘中读出进行复原的过程.

3.1 状态存档实现

针对前面介绍的存档的过程,首先系统中的逻辑时钟设置为T,为稳定严格递增序列.这里采用交替使用存档模板来进行存档数据,基本实现方式如图2所示.采用多模板的设计,模板即按照逻辑时钟将一段时间分成多个区间并且每个区间用时间桶表示,通过模板之间的拼接形成完整的时间序列,为了简化对模板的操作,模板应当根据逻辑时钟T的粒度,将模板分成的时间桶数量最少要大于ε.

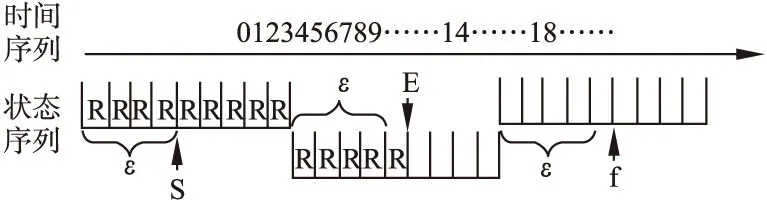
图2 多模板存档图Fig.2 Multiple template storage diagrams

在多模板的状态序列生成过程中的方式序列的生成过程可以分为如下几个步骤:

Step 1.初始化

在逻辑时钟的0时刻从按照偏移ε找到S位置,系统的初始化的状态写入模板对应的[0,S]的区间内,标记第一个模板的首个桶代表的逻辑时钟是-ε.

Step 2.新状态添加

生成新的状态添加到当前的模板中,首先查看当前的逻辑时钟T,将数据写入桶中对应的[T-ε,T]的位置里,状态需要附带逻辑时钟属性,表明当前状态发生的时间节点.

Step 3.模板拼接

随着逻辑时钟的前进,当前模板表示的逻辑时钟范围用尽,则通过两个模板拼接,拼接之后可以看成是连续的时间模板,随着逻辑时钟的进一步推进,模板拼接分为以下几个步骤:

步骤1.一个模板随着逻辑时钟的推进,当一个模板被首次使用的时候,会标记它第一个桶所对应的逻辑时钟,之后按照每个桶针对首个桶的偏移计算对应的逻辑时钟.

步骤2.当状态数据添加的位置超过一个模板的第ε个位置,即达到如图2所示的E的位置时,此时可以认定前面一个模板的数据不会再发生改变,可以将其持久到磁盘中.

步骤3.当一段相当长的时间不添加新的状态,此时状态已经不会在写入到如图2的第二个模板中的,并且逻辑时钟跨越了多个模板,当这样的状态产生时,则从重新生成一个新模板,记录新模板的首个时间桶的逻辑时钟为T-ε,并从新的模板ε处开始添加状态数据.然后将前面两个模板进行数据的持久化.

磁盘持久化过程描述如下:操作采用单线程线程池方式,接收任务后按照线程加入顺序执行,这种方式可以保证写入的顺序性.线程池执行的线程的基本逻辑是按照模板的先后顺序将模板中的数据从前向后扫描然后写入到一个固定的磁盘文件,每个桶中的提取可以使用先入先出的方式.系统中由于状态数据跨越时间跨越较大等原因可能需要多个模板,此时可以将模板作为一种资源池化,从而降低模板生成和销毁的开销.

3.2 状态复原实现

状态的复原并不涉及复杂的逻辑计算和交互行为,本小节介绍单线程驱动模型来说明将数据恢复的过程的实现.前面提到了在恢复的过程可能会涉及到状态的排序、逻辑时钟节点T的确定等问题.首先针对排序问题进行进行处理是采用单个的模板进行排序操作,基本方式如图3所示.

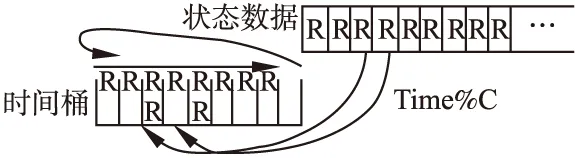
图3 状态恢复图Fig.3 State recovery diagram

这里采用的方式在单线程模式下,仅使用一个存档模板,这个存档模板同样按照逻辑时钟的粒度将时间分割成一个个连续的时间桶.模板分割的时间桶的数量C要严格大于ε.执行过程如下:首先批量加载磁盘中的数据,依据状态数据的逻辑时间戳Time,通过Time%C的值作为索引将状态添加到对应位置的时间桶中,这里一个时间桶里面可能有多条状态数据,先加入时间桶中的数据在最前面,后加入的在时间桶的后面,采用先进先出的方式,可以理解为每一个时间桶为一个队列.在桶的数量严格大于ε的情况下,可以避免桶中数据加入的过程中,逻辑时钟时间戳靠后的状态在一个桶中时间戳靠后的状态数据之前,从而在遍历桶中数据时只要发现当前逻辑时钟与桶中状态数据的时间戳的差值大于ε,则认为不是当前逻辑时钟的状态数据,然后顺序遍历下一个桶中的状态数据.

处理方式可以总结为如下几个步骤:

步骤1.批量读取状态数据文件中的状态,并根据Time%C的方式将其加入到当前的桶中.同时记录每批最后一个状态数据的时间戳t.

步骤2.当发现时间戳t>T+ε的状态数据时,停止批量加载的过程,开始按照逻辑时钟的速率,将加载的状态按照当前逻辑时钟推进T时间节点.

步骤3.逻辑推进过程按照逻辑帧率从对应的桶中取出数据,此时需要判断是否是当前帧的数据,即当前的逻辑帧和桶中包含状态的时间戳进行对比,如果当前状态数据的时间戳与逻辑时钟的差值小于ε(通常会比ε小很多,比较结果是两者相近或者差值较大,差值大于等于ε或者接近于0),如果差值大于ε则不在当前逻辑帧中,停止执行当前逻辑帧,如果小于ε则执行状态数据并且在桶中删除这条状态数据,重复步骤3.

时间桶的大小是固定的,复原线程按照状态数据的逻辑时钟的时间戳加载到对应的时间桶中,并且按照与状态存档时相同的逻辑时钟执行,每一个逻辑帧处理一个桶中当前帧的数据,并且是循环执行,当执行时间桶的结尾时,再次从时间桶的开头进行处理.实际上将上面的单线程模型扩展为双线程模型时,任务分解为加载线程来负责数据的排序和批量加载到时间桶,另一个线程通过按照帧率来进行状态数据的处理,当加载线程处理的添加状态的逻辑时钟大于处理线程C个逻辑时钟时,两个可以独立运行并且相互不冲突的,其中C为模板的时间桶的个数.

4 实验结果与分析

本模拟实验的硬件平台Intel Core(TM)i3-4160 3.6GHz四核处理器物理机1台,内存为8GB,算法的实现与测试均采用Java语言.

其中对所提出的状态存档方法进行性能验证,主要变量有每逻辑帧的并行度以及ε偏移等,评估指标为CPU使用率、逻辑帧率等,其中参与对比的方法为传统多线程状态追加方式.

4.1 实验方法

在状态存档过程中,通常状态改变时会涉及到对象属性的一个数据切面的变化,例如控制运动的线程会同时改变位置、朝向等多个数据.为了使得模拟实验的基本环境相同,这里采用首先生成一定数量的数据(Component),这些Component逻辑代表实际对象的状态改变的内容.为了使得这里的数据具有一般性,数据采用如图4所示的定义,并将所有Component离散加载在内存中来避免连续的Component排列因CPU Cache影响性能测试.

首先所有的数据的参数i和data的大小都是采用正态分布随机生成一定期望范围内的值,并且在测试之前进行存储,针对在测试不同参数和方法的时候,每一种都是使用同一份数据集;针对不同的参数和方法分别在相同的数据集合上测试多次取平均值,并以相同的方式测试不同的数据集合,最终取平均值作为评估结果.

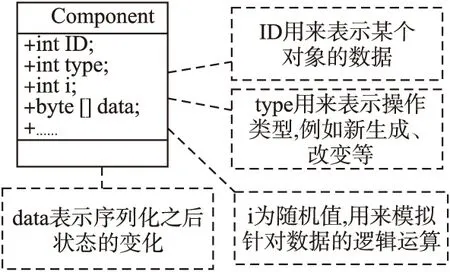
图4 状态结构图Fig.4 State structure diagram

数据的持久化采用如图5所示的定义,状态信息在存储时需要包含逻辑时钟时间戳.逻辑时钟时间戳用来表明状态改变时对应的时间节点.

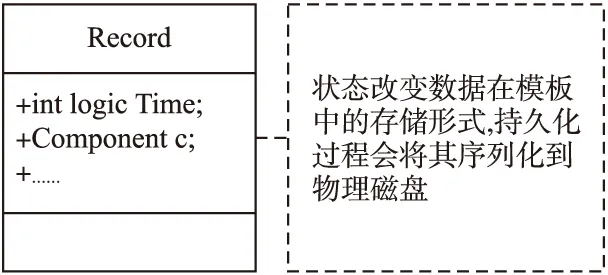
图5 状态存档图Fig.5 State storage diagram

4.2 实验结果分析

针对以上实验的设计,实验的对比结果如表1所示.其中针对本文所介绍的方法的ε的值为100个逻辑时钟的大小,同时设定逻辑帧率的状态数据总量为定值,将状态总量分配到不同线程中执行并计算相关指标.

表1 性能对比表
Table 1 Performance comparison

方法指标并行数量(个)逻辑帧率/fpsCPU使用率/%传统多线程状态追加方式129422486346986本文方法127432516547290

实验结果分析,当线程并行数量为1时,即为传统单线程执行方式中,采用追加的方式要优于本文所提出的方法,原因主要是单线程下本文所提方法中需要处理的模版操作要更复杂,同时由于不能利用多核优势,CPU使用率以及逻辑帧率较低.传统方式和本文方式在多线程下都获了很大程度的加速,但是本文所提出的方法由于减少了在状态存档过程中的冲突概率,性能要优于传统状态追加的方式,同时由于降低了冲突率,CPU的利用率获得一定程度的提高.并且由于针对偏移量的严格定义,本文所提出的方式可以严格的保证在状态恢复过程的时序性,比传统追加的方式在理论上对于时序性的保证更加可靠.传统状态追加的方法与本文所提的方法在并发数增加到2时逻辑帧率提高幅度接近一倍,但逻辑帧率再次增加时逻辑帧率提高幅度比率降低,主要因素有并行场景中存在并发调度以及加锁等耗时操作.

针对ε值的选择,实验结果如图6所示,通过前面的理论分析和实验验证,实际上当ε大约大于二倍并行数量时,此时对于ε的继续增大并不会对性能提升产生明显影响.同时发现当线程数量过多的时候,性能并不会继续提升反而会下降,对于实验分析和解释是,本方法中的大部分线程处理逻辑本身属于计算较密集型的,当线程数量过多的时候会导致CPU的上下文切换反而增加了时间开销.实验结果表明,在多核处理器的操作下,并行数量应当小于等于物理机器的核心数量.

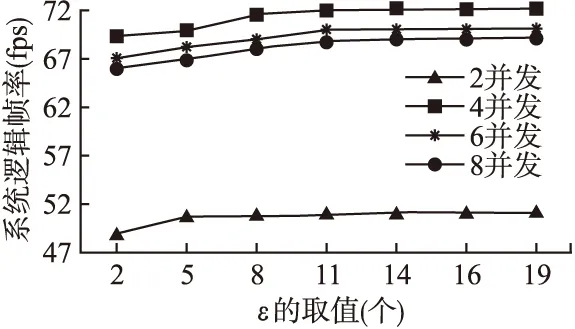
图6 ε与并行度关系Fig.6 Relationship of concurrency and ε

从实现复杂度以及适用性角度分析,本文所提出的方法主要的运用的数据结构是上文所提出的时间模板,原则上使用数组结构即可完成设计,与无锁队列等实现方式相对,减少了很多高级复杂的原子元语操作的过程,在工程实践层面非常易于实现,并且保证了更加严格的时序性.同时,本文所提出的方法针对并行系统的日志记录等场景下的冲突问题同样具有借鉴意义.

5 总结与展望

本文提出一种在并行系统下状态存档的冲突消减方法,本方法充分分析了状态存档写入冲突发生的原因、时序性的含义等问题.通过对这些问题的深入研究,提出了一种不严格时序方法,主要体现在主动引入偏移量ε,通过偏移量ε将状态存档的偏移度保持在一定的范围内,从而解决并行系统存档过程中追加方式造成的冲突.同时通过确定性的定义ε范围,可以合理的利用数据恢复过程中批量加载的特性,对偏移量ε内的数据进行有效的排序,通过数学分析和理论证明以及实验验证,证明了本方法的有效性和正确性.

针对本文所提出的方法,接下来的工作主要从以下几个方面来进行强化,第一,当前的算法与ECS(Entity-Component-System)模型进行整合,根据ECS模型的特点进行优化.第二,在状态存档文件上建立有效的索引机制,通过索引机制实现快速跳跃复原等功能.