基于改进型量子粒子群优化算法的汽轮机流量特性优化研究

2019-12-04雷志伟武海澄周海雁阚俊超

热力发电 2019年11期

雷志伟，张兴，武海澄，周海雁，阚俊超，李达

（中国大唐集团科学技术研究院有限公司华东电力试验研究院，安徽合肥 230031）

汽轮机流量特性是指机组主蒸汽流量指令与主蒸汽流量间的函数关系，是机组协调控制、涉网性能调节、安全稳定运行等方面[1]的重要特性。汽轮机流量特性不佳会影响发电机组运行的安全性[2-3]、经济性[4]和稳定性。目前，常见的汽轮机高压进汽部分由2 个、4 个或6 个高压调节阀组成，其运行方式分为单阀运行和顺序阀运行。为了提高机组中低负荷段发电效率，通常采用顺序阀运行方式。

电网深度调峰和深度节能工作的持续推进，对传统火电机组提出更大考验。通过汽轮机流量特性优化，进一步挖掘汽轮机节能潜力，提升汽轮机进汽流量控制的稳定性和快速性，有利于促进火电机组主要调节系统调节品质的改善。

近年来，国内外学者及工程师在汽轮机流量特性领域进行了相关研究。张锐锋等[5]通过调节阀流量特性测试与仿真验证相结合的方法，优化其线性度和连续性，取得了一定效果。王刚等[6]采用K-Medoids 算法，以历史数据挖掘为基础，提出了一种新的汽轮机流量特性线性优化方法，极大地节省了优化时间和精力。文乐等[7]利用动态数据挖掘，实现了汽轮机调节阀流量特性的实时在线计算。文献[8]采用基于模型自适应算法，实现汽轮机流量特性的自动优化，解决了其线性度自动优化的难题。

汽轮机流量特性不仅与阀门本体、汽轮机通流部分结构、调节级临界压比等有关，还与阀门配汽函数、蒸汽温度等实际运行参数有关。当某种因素造成汽轮机流量特性不匹配时，需要重新优化阀门配汽函数，以改善汽轮机流量特性和提高机组节能潜力。本文以挖掘机组节能潜力与优化汽轮机流量特性线性度为双目标，提出基于改进型量子粒子群优化算法（quantum-behaved particle swarm opti mization algorithm，QPSO）[9]的汽轮机流量特性节能优化技术；通过智能群体寻优技术和高精度的汽轮机流量特性仿真模型，解决困扰该技术领域阀门重叠度与汽轮机流量特性线性度耦合的优化难题。

1 汽轮机流量特性数学模型

1.1 汽轮机流量控制模型

图1是常见汽轮机阀门控制程序流程。机组流量指令经调节阀控制系统函数依次映射，输出各个调节阀开度指令，用以控制汽轮机主蒸汽流量。

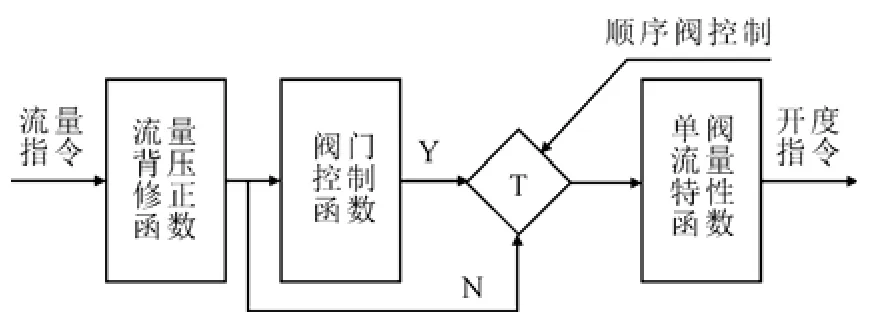
图1 机组流量生成示意Fig.1 Schematic diagram of the unit flow generating

汽轮机阀门控制程序可以视为一个单输入单输出的非线性系统[10]。该系统的输入X为机组流量指令，通常X∈[0,100]；系统的输出为机组的蒸汽流量G。机组在顺序阀运行方式下，汽轮机阀门流量函数G的表达式为

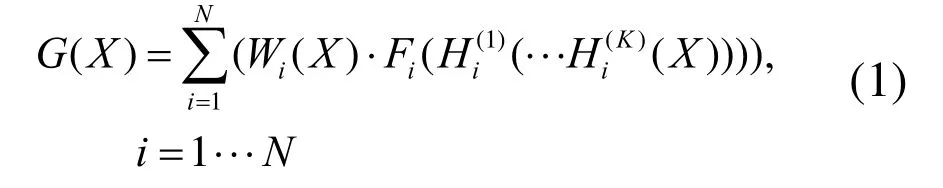
式中：N为机组阀门数量；Wi(·)为第i个阀门流量的权值函数，Wi(X)⊆(0,1)；Fi(·)为第i个阀门的单阀流量特性函数，是指通过试验获取的每个阀门的阀门开度-流量函数；Hi(K)(·)为数字电液控制系统（DEH）中第i个调节阀的第K个阀门控制函数；K值与DEH 的结构类型有关，通常K∈{1,2,3}。

由式(1)可知：通过若干个插值函数的非线性映射后，模型输出汽轮机阀门的总体流量；在顺序阀方式下，机组流量特性函数G与DEH 阀门控制函数H、单阀流量特性函数F、权值函数W息息相关。

1.2 主蒸汽相对流量计算

通常根据汽轮机流量特性测试数据建立数学模型。汽轮机主蒸汽相对流量是指机组在某一流量指令下，经过汽轮机阀门的蒸汽流量占机组总流量（流量指令为100%时）的百分比。其计算方法建立在流量特性试验测量或数据挖掘[7,11]的基础上，但无论哪一种，基本采用弗留格尔[12]近似公式

式中：G′分别为变工况前后总流量，p01、p0，t01、t0和pg1、pg分别为变工况前后调节级蒸汽压力、蒸汽温度和高压缸排汽压力。对于超（超）临界机组，在不同负荷段下，阀门蒸汽温度变化比较大，需要加以修正。

汽轮机流量特性数学模型描述的是机组流量指令与相对流量的函数关系。结合式(1)、式(2)，可以建立较高精度的汽轮机流量特性数学模型，用以描述当前机组流量特性的优劣状况。

2 改进型QPSO 的双目标优化

由式(1)可以看出，在顺序阀方式下，各个阀门开启次序由其阀门控制函数决定。本文在优化前先将几个阀门控制函数整合为1 个单值函数H，以便于优化算法的分析和计算。阀门重叠度是指当前一个阀门开度达到100%时，后一个阀门所开启的开度值，其大小与阀门控制函数H有关。

为了优化汽轮机阀门流量特性和挖掘机组节能潜力，需要同时解决阀门重叠度与流量特性线性度的双目标优化问题。

2.1 改进型QPSO

QPSO 是一种基于智能群体协作的全局优化算法。群体中的每一个粒子均具有量子行为特性，该特性是指在某种吸引势能场中，粒子以一定的概率密度出现在定义空间中的任意位置。在收敛的过程中，粒子不断靠近群体中的吸引子，直到落入其中，整个群体具备聚集性特征[13-14]。QPSO 相较于其他智能群体算法，具有较强的鲁棒性和较快的收敛速度。本文通过改进型QPSO 适应度函数和位置更新公式，使新算法能够同时兼顾双目标优化的特点。

设定QPSO 中的种群数为M，其随机分布在1 个Dim 维的目标寻优空间中。该空间中的粒子个体最优位置zi=(zi1,zi2,…,ziDim),i=1,2,…,M，而此时QPSO 全局最优位置si=(si1,si2,…,siDim),i=1,2,…,M。搜索过程中，不断记录此时群体中粒子最优解zbest和全局最优解sbest。引入群体中所有粒子个体最优位置的平均值，记为meanz，表示种群zbest的中间位置，其表达式为

式中，zi为第i个粒子的个体最优位置zbest。

根据粒子此时的个体最优位置和全局最优解得出吸引子Y的位置，记为

式中，为(0,1)之间的随机数。

结合式(3)、式(4)，位置更新公式为

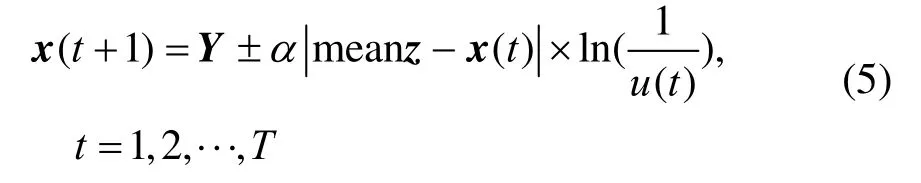
式中：t为当前迭代次数，T为最大迭代次数，u(t)为(0,1)上的均匀分布的概率密度函数；引入收缩膨胀因子，控制单个粒子的收敛速度，同时为了提高单个粒子的收敛性，的数值一般不大于1.782。

量子粒子群中的粒子在寻优的过程中容易局部收敛。为了防止粒子过早陷入局部最优解[15]，在原有QPSO 的基础上进行改进，强调在寻优初期拓展粒子的搜寻范围。因此，在计算个体最优位置时，加入1 个扰动量，

式中为扰动调整因子。

根据需要，合理选择扰动调整因子，使得加入的扰动量既不影响寻优的方向，又能避免陷入局部最优。

在循环迭代中，群体中的粒子不断地靠近吸引子的位置，直至落入其中。在达到最大迭代次数或误差精度后，输出群体的全局最优值sbest。

2.2 改进型QPSO 的适应度函数

顺序阀方式下，汽轮机流量特性的线性度由控制函数H、流量权值函数W、单阀函数F决定，流量权值函数W和函数F由流量特性试验获得。

为了兼顾流量特性线性度和阀门重叠度的双目标优化，改进型QPSO 事先随机搜索阀门重叠度θ，再计算当前重叠度进行流量特性线性度优化。θ由控制函数H决定：

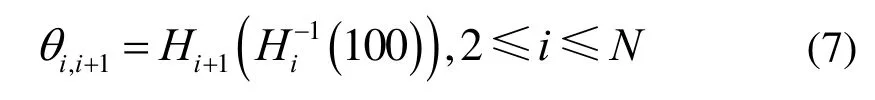
线性度目标函数[16]D一般可采用一维线性函数、正比例函数等。根据式(7)的重叠度对D进行分段优化，分别对应各个阀门所控制的流量区间Di。结合式(1)，汽轮机流量特性线性度优化计算式为

式中，、为双目标权值系数，一般、[0,1]，用于调整双目标之间性能指标的权重。

改进型QPSO 的双目标优化算法，经过多次循环迭代后，或当适应度函数值J达到精度要求0.05（满足生产需求）时，输出最优控制函数H和阀门重叠度θbest，能够在实现汽轮机流量特性线性度优化的同时，实现阀门重叠度和机组节能优化。算法流程如图2所示。

3 阀门流量特性优化

3.1 机组特性分析

某电厂1 号机组DEH 采用4 个阀门控制汽轮机进汽流量，其顺序阀次序为GV1/GV2-GV3-GV4。DEH 阀门控制函数采用折线函数。优化前，DEH阀门控制函数见表1，阀门控制函数曲线如图3所示。经计算，GV1/GV2 与GV3 重叠度（重叠度1）达到100%，GV3 与GV4 重叠度（重叠度2）为16.62%，即GV1 和GV2 在整个行程下均有节流情况。在顺序阀方式下，测试机组汽轮机流量特性[17]，并按照式(2)计算机组相对流量，测试结果如图4所示。由图4可见：曲线斜率变化较大，整体线性度不佳；其与线性度目标函数(D(X)=X)的标准差约为3.554%。

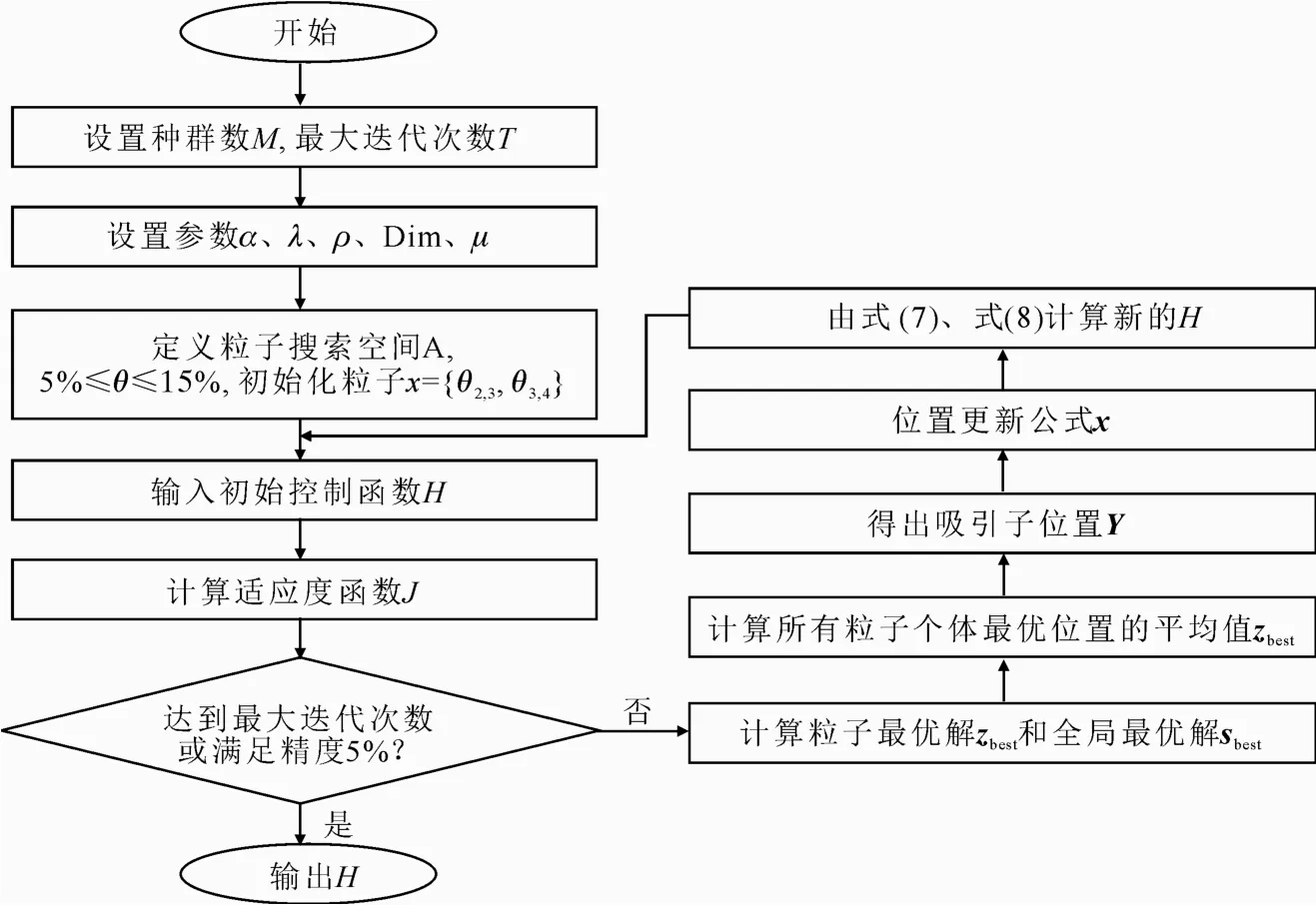
图2 算法流程Fig.2 The flow diagram of the algorithm

表1 优化前DEH 阀门控制函数Tab.1 The DEH valve control function before the optimization %

图3 优化前DEH 阀门控制函数曲线Fig.3 The curves of DEH valve control function before the optimization

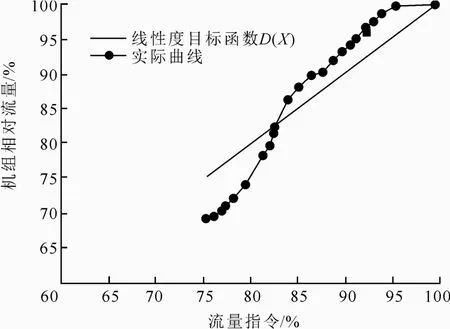
图4 优化前阀门流量特性Fig.4 The valve flow characteristics before the optimization

3.2 仿真优化

3.2.1 构造解空间

利用改进型QPSO 双目标优化算法，根据3.1测得的汽轮机流量特性试验数据建立仿真优化模型。结合图3阀门控制函数的曲线特征，GV1 与GV2 的控制函数H1=H2，构造粒子群的解空间A，

结合实际机组运行及阀门结构限制，阀门之间的重叠度越小，越容易造成在重叠区间阀门晃动、机组功率振荡等不稳定工况[18-19]，因此需要对重叠度加以限制，本文采用5%≤θ≤15%。

3.2.2 不同扰动调整因子下的收敛性对比

扰动调整因子μ的取值影响改进型QPSO 的收敛性。为了使算法快速收敛且双目标函数J满足精度要求，实现汽轮机流量特性线性度与重叠度优化，对不同u时双目标函数J的变化趋势进行讨论。

设置种群数M=200，最大迭代次数T=5 000，选取a=1.6、λ=1.0、р=0.1、Dim=2。在=1、0.1、0.01 时进行顺序阀方式下的仿真优化，各项指标如重叠度1、重叠度2、流量特性与目标函数的标准差||G-D||和双目标函数J对比情况见表2。由表2可见：当值取过大或过小时，造成算法寻优前期的扰动量过大或不起作用，使量子粒子群极易陷入局部最优解，无法取得较好的优化效果。因此，u值一般取0.05～0.5。

表2 不同值下仿真对比Tab.2 The simulation results with different values

指标扰动调整因子μ 1 0.1 0.01重叠度1/% 15.000 7.150 12.175重叠度2/% 13.352 9.410 13.511||G-D||/% 2.927 0.752 1.378 J/% 5.362 2.625 3.897

图5为当=0.1 时，优化后的DEH 阀门控制函数曲线，对应数据见表3。

图5 优化后DEH 控制函数曲线Fig.5 The curves of DEH valve control function after the optimization

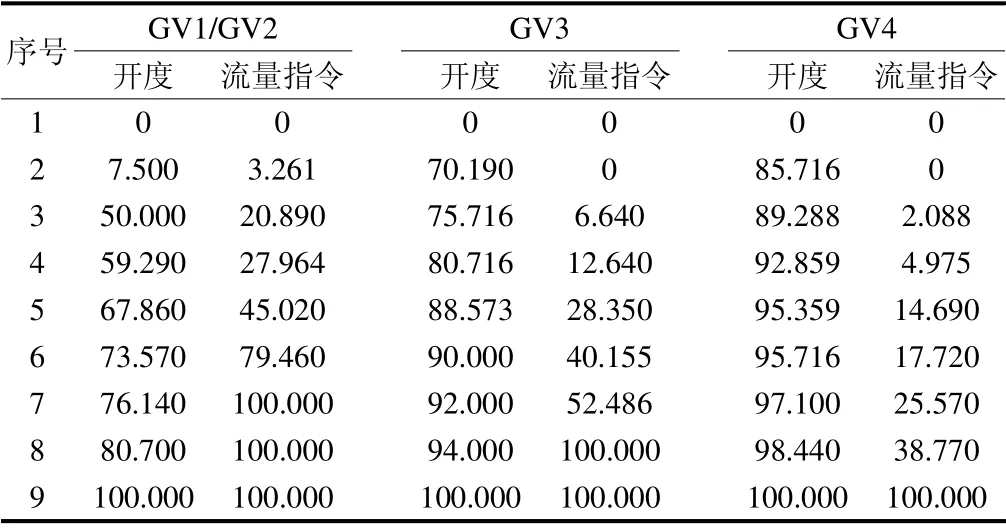
表3 优化后DEH 阀门控制函数Tab.3 The DEH valve control functions after the optimization %

计算可知：GV1/GV2 与GV3 的重叠度为7.150%，GV3 与GV4 的重叠度为9.410%，相较于原阀门重叠度均减小，线性度也得到了改善，满足优化精度0.05 的要求。

3.3 实际应用

为了验证仿真优化的实际效果，将表3中的函数应用至1 号机组DEH 阀门管理程序中。

优化后对机组开展汽轮机流量特性测试工作，并根据式(3)计算主蒸汽流量，测试结果如图6所示。由图6可知，优化后，实际汽轮机流量特性曲线与线性度目标函数D的标准差为0.969%，与仿真结果相差无几。考虑到实际生产中的数据精度和噪声等因素，该结果能够满足生产需求。基于改进型QPSO 的双目标优化算法，结合了汽轮机流量特性线性度和阀门重叠度的双优化，消除了原有汽轮机流量特性曲线突变，提升了整体流量控制的线性度，验证了仿真优化的效果。

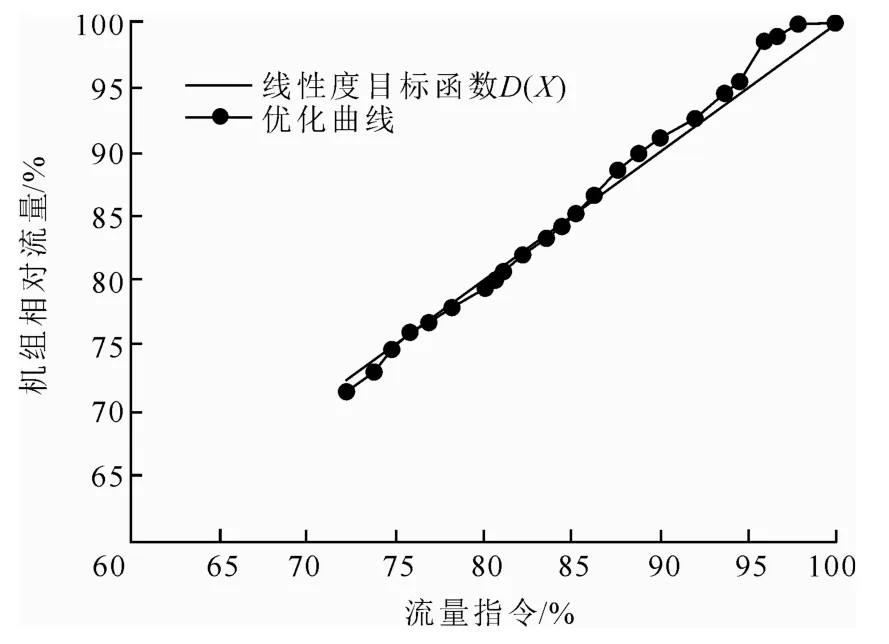
图6 优化后阀门流量特性Fig.6 The valve flow characteristics after the optimization

4 阀门流量特性节能分析

4.1 主蒸汽压损分析

为了进一步分析优化后的节能情况，采集1 号机组在汽轮机流量特性试验工况下的主要参数，用以对比优化前后汽轮机主蒸汽压损的变化情况，结果如图7所示。

在高负荷区间，由于调节阀基本处于全开状态，由阀门节流产生的蒸汽压损情况基本相当；但是在中低负荷段，由于优化后各阀门间的重叠度降低，GV1 和GV2 开度相较于优化前大，节流损失减少，因此优化后的主蒸汽压损显著减小，蒸汽品质得到提升。

同时从图7可以看出，机组流量指令在75%～100%的运行区间时，主蒸汽压力波动值较优化前减小，有利于提高机组负荷、主蒸汽压力等自动控制的品质。因此，改进型QPSO 的汽轮机流量特性节能优化效果较好。

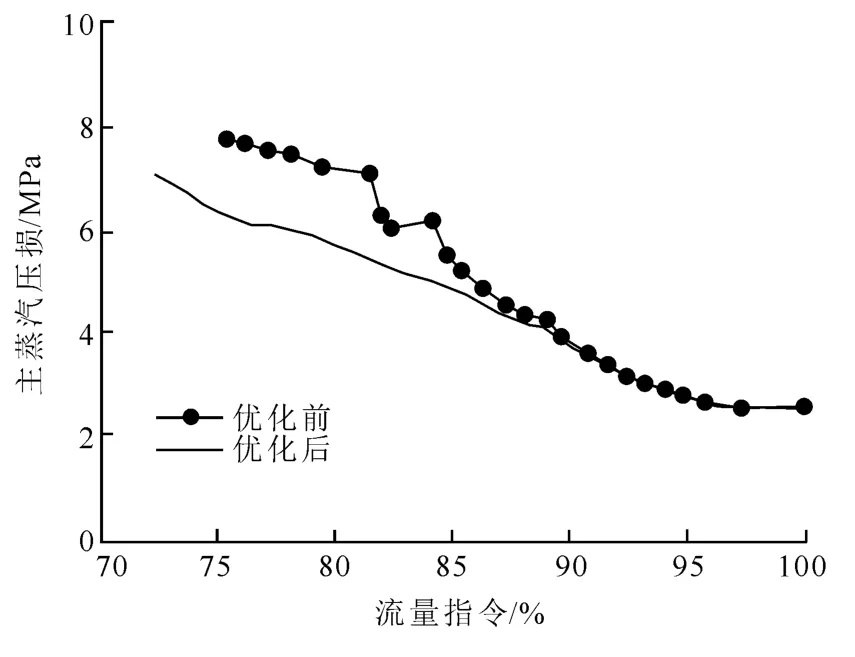
图7 主蒸汽压损分析Fig.7 The main steam pressure loss analysis result

4.2 汽轮机热耗率分析

进一步分析汽轮机流量特性优化后的节能效果，计算和对比优化前后汽轮机热耗率的变化情况[20]。大多数机组给水流量测点较主蒸汽流量测点可靠，因此采用以给水流量为基准值计算热耗率。高压加热器（高加）及除氧系统示意如图8所示。

图8 高加及除氧系统示意Fig.8 Schematic diagram of the high pressure heater and deaerator system

通过除氧器、高加等设备上对应的参数测量和计算，确定主蒸汽流量和再热蒸汽流量；针对再热回热式汽轮机，进行高加热平衡计算，得出各高加和除氧器的抽汽量和最终给水流量；查询各工质焓值，可计算出试验热耗率HR，其计算公式为[12]

式中，Dm为主蒸汽质量流量，t/h；Dr为再热蒸汽流量，t/h；Dfw为给水流量，t/h；Dcr为冷再热蒸汽流量，t/h；Dshs为过热减温水流量，t/h；Drhs为再热减温水流量，t/h；hm为主蒸汽焓，kJ/kg；hr为再热蒸汽焓，kJ/kg；hfw为给水焓，kJ/kg；hcr为冷再热蒸汽焓，kJ/kg；hshs为过热减温水焓，kJ/kg；hrhs为再热减温水焓，kJ/kg；Pe为汽轮机组功率，MW。

采集优化前后机组日常运行时，各个稳态负荷段下的主要参数。优化后，机组在400 MW 工况下的主要工质焓值见表4。通过表4等数据，根据式(11)计算出机组的平均热耗率，优化前后机组热耗率对比如图9所示。

表4 优化后400 MW 工况下主要工质焓值Tab.4 The enthalpy of main working fluids at 400 MW load after the optimization kJ/kg

图9 机组热耗率对比Fig.9 The unit heat rates before and after the optimization

对比分析图3和图5可以看出：在流量指令60%～80%，优化前GV1/GV2 开度处于30%～50%，此区间阀门流量变化较大，节流损失大；而优化后由于重叠度和阀门控制函数得到优化，GV1/GV2开度处于35%～100%，使得节流损失较小。因此，优化后，中低负荷段阀门节流损失减少，在该负荷区间汽轮机热耗率平均降低了约34.31 kJ/(kW·h)，节能效果较为明显（图9）。