Quasi-Z源逆变器纹波自注入APF及其控制策略

李志勇 王思君 陈有根

摘要：单相Quasi-Z源逆变器交流侧二倍基波频率（二倍频）的功率脉动会使其直流侧不可避免的出现二次纹波。针对单相Quasi-Z逆变器直流侧电感二倍频电流纹波问题提出了一种自注入APP控制策略。运用状态空间平均法研究二倍频能量的传递机理，结合Quasi-Z源网络小信号模型，发现占空比扰动可以影响Quasi-Z源网络能量分布。在直通占空比上叠加補偿信号，在不改变电路拓扑结构的前提下，利用Quasi-Z源网络向逆变桥自注入二倍频能量，抑制Quasi-Z源网络输入功率波动。仿真验证了所提控制策略的有效性，Quasi-Z源网络输入电流纹波幅值降低了81.4%，并结合反馈控制方法对所提控制的响应速度进行了仿真对比分析。

关键词：Quasi-Z源逆变器;纹波;传递机理;自注入

DOI：10.15938/j.emc.2019.10.009

中图分类号：TM 464文献标志码：A 文章编号：1007-449X（2019）10-0077-08

0引言

Quasi-Z源逆变器是具有升压逆变一体化的特殊结构，自提出以来即受到了广泛的研究和关注。从拓扑结构上看，单相Quasi-Z源逆变器本质上由Quasi-Z源网络和VSI（电压源型逆变器）级联组成。变流装置VSI的存在，必然会导致其交流侧存在二倍频率功率，进而引起直流侧产生二倍频的纹波，影响逆变器的运行品质。Quasi-Z源网络是一个由电感和电容组成的无源网络，具有一定的滤波能力。采用较大参数的电感和电容可以有效抑制二倍频的纹波，但是增加了Quasi-Z源逆变器的体积和成本，但若不抑制这些低频纹波，会影响Quasi-Z源逆变器的控制精度，降低器件的使用寿命。这些原因限制了Quasi-Z源网络在光伏发电、电机控制等对直流电源波动敏感领域的应用。采用合适的方法，对Quasi-Z源逆变器二倍频功率进行主动补偿，进而抑制二倍频纹波，对于提高其运行品质，拓宽应用领域具有重要意义。

目前针对Quasi-Z源逆变器二倍频功率的主动补偿方法主要有2种。一种是利用有源滤波思想添加额外带储能环节的拓扑支路，在逆变桥输人端或输出端对二倍频功率进行主动补偿。另一种则考虑Quasi-Z源网络本身是一个可控的储能网络，并且抑制的主要目的是在于稳定Quasi-Z源网络输入功率，在传统控制的基础上添加额外控制或滤波支路，抑制Quasi-Z源逆变器二倍频功率向前级流动。

文献提出运用有源滤波的思想，添加带有电容或蓄电池作为储能元件的额外支路，对逆变器交流侧产生的二倍频功率进行补偿，抑制Qua-si-Z源逆变器二倍频功率的流动。一方面，添加额外支路改变了Quasi-Z源逆变器的拓扑结构，增加了成本。另一方面，额外支路亦需要添加额外的控制策略，增加了控制的复杂度。理论上，此类控制方法可以对逆变桥生成的二倍频功率完全补偿，但在逆变器实际运行过程中直流电源输出功率允许在一个合理的范围内波动。

为此，部分学者提出利用Quasi-Z源网络储能可控的特点，对原有控制策略进行改进，利用Quasi-Z源网络能量对二倍频功率进行自注入式补偿。此类方法不改变Quasi-Z源逆变器拓扑结构，在保证Quasi-Z源网络升压能力的前提下，将其作为一个有源滤波装置，在原有电路的基础上构建虚拟APF也可以有效解决二倍频纹波问题。

在Quasi-Z源逆变器中，传统控制策略均在开关周期的固定位置插入直通占空比，Quasi-Z源网络电感电流开关周期平均值并不固定。文献提出通过改变开关的插入直通占空比的位置，抑制电感电流的波动。通过对Quasi-Z源网络建模分析，占空比扰动可以改变网络电容电压和电感电流，即改变占空比大小以可以控制网络能量状态。文献采样直流电源支撑电容电压，通过比例控制器跟随其直流分量，将生成信号叠加至稳态占空比，实现了光伏电池输出功率的稳定。直流电源支撑电容目的在于稳定直流电源的输出功率，若采用合适控制策略后，可以由Quasi-Z源网络承担支撑作用。文献在拓扑结构上取消了直流侧支撑电容，直接提取直流侧电源输出电流的交流分量，与参考值比较后通过PI控制器对占空比施加扰动。本质上看，文献均采用了反馈控制的思想，通过Quasi-Z源网络向逆变桥补偿二倍频功率，抑制二倍频功率向直流电源端的传递。本质上，二者均属于反馈控制，虽然具有较高的控制精度，但是，动态响应特性较差。

本文将Quasi-Z源逆变器分为Quasi-Z源网络和VSI 2个二端口网络，通过分别研究2个二端口网络的输入输出关系，结合二者的连接关系，分析了二倍频功率在Quasi-Z源逆变器中的传递机理。以Quasi-Z源逆变器的传递机理为基础，将交流侧二倍频能量作为扰动，提出了一种基于前馈思想的自注入式APF控制策略。仿真验证所提控制策略对二倍频功率传递的抑制效果，并与采用反馈思想的控制策略在动态性能上进行了对比。

1二倍频纹波传递机理

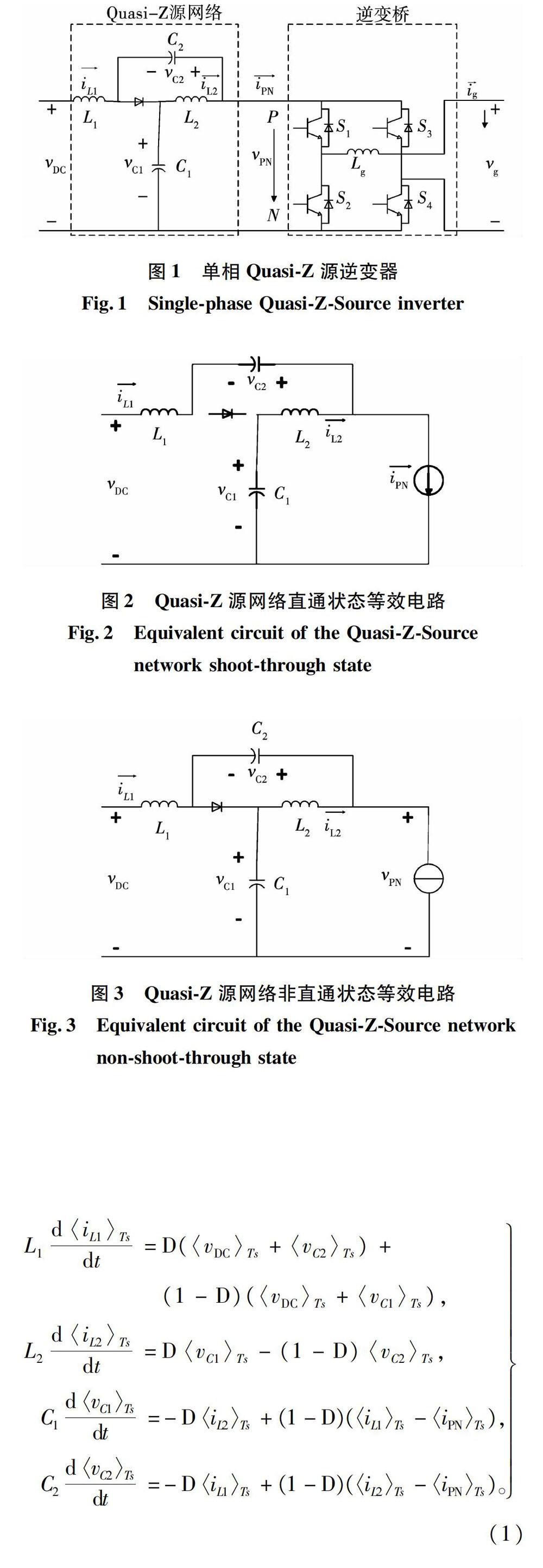
单相Quasi-Z源逆变器拓扑结构如图1所示，由电感L₁、L₂和电容C₁、C₂组成的Quasi-Z源网络以及逆变桥组成的传统逆变器2个二端口网络级联构成。Quasi-Z源网络和逆变桥的一部分组成了升压电路，将输入直流电压υ_DC升压后作为逆变桥的直流输入υ_PN。由开关管组成的传统逆变器，将前级直流输出υ_PN逆变为交流输出υ_g。足功率守恒原理，传统逆变器直流输出电压υ_PN必然会产生二倍频功率波动。为研究二倍频功率在Quasi-Z源逆变器中的传递机理，分别分析Quasi-Z源逆变器的2个二端口网络，确定Quasi-Z源逆变器输入和输出之间的关系。

1.1Quasi-z源网络模型

Quasi-Z源网络运行时，可分为直通和非直通2种工作状态。直通工作状态时同一桥臂开关器件同时导通，其等效电路如图2所示，此时电容处于放电状态，电感处于充电状态，二极管被反向截止。非直通状态下，二极管导通，电感处于放电状态，电容处于充电状态，如图3所示。

结合图2和图3，采用状态空间平均法，可以得到Quasi-Z源网络大信号模型为式（1），其中（x）_Ts代表狀态变量x在一个开关周期的平均值。式中：i_L1、i_L2为电感L₁和L₂的电流;υ_C1、υ_C2为电容Cl和C，的电压;L₁，L₂、C₁、C₂分别为Quasi-Z源网络电感和电容;υ_DC为Quasi-Z源网络输入电压;i_PN为Quasi-Z源网络直通状态下输出电流;D为Quasi-Z源网络直通占空比。

当Quasi-Z源网络运行在稳态时，电感电流与电容电压的开关周期平均值为常数，即式（1）等号左侧部分为零。可以得到稳态时QuaSi-Z源网络输入和输出电流的关系为

其中，I_DC、I_L1、I_PN分别为Quasi-Z源网络稳态时的输入电流、电感L₁的电流、Quasi-Z源网络非直通状态时的输出电流。

1.2Quasi-z源逆变器输入电流分析

图1所示右侧虚线框为逆变器拓扑结构图，S₁，S₃为逆变电路开关函数，当开关函数为1时，对应开关器件导通，为0时对应开关器件关断。

由图4可知，逆变器输出电流：

i_PN=S₁i_g-S₃i_g（7）

结合文献[18]，可将开关函数S₁，S₃进行傅里叶级数展开，由于高次分量在通过Quasi-Z源网络时电容导通，因此可以省略高频部分后S₁，S₃逆变开关函数表达为

由式（2）可以看出，后级逆变器所产生的直流分量传递至Quasi-Z源网络输入端仍为直流。而后级逆变器所产生的交流分量，结合式（4）可以看出必然会引起Quasi-Z源网络输入端波动。即Quasi-Z源逆变器工作时，Quasi-Z源网络运行在稳态工作点附近。结合式（4）和式（10）可以得到Quasi-Z源逆变器输入电流波动为

若单位功率因数为ρ并网时，上式的时域形式为

2纹波自注入APF控制策略

当Quasi-Z源逆变器工作时，其输出电压为V_gsinwt、输出电流为I_gsin（wt+ρ）。由于电感电流和电容电压存在扰动，根据功率守恒原理应该有：

上式中等式左右两侧直流分量应相等，交流分量亦然。因此可进一步得出Quasi-Z源逆变器工作时交流功率流动关系如式（14）所示：

结合式（4）和式（10）以及上式可以得出Quasi-Z源逆变器未进行纹波抑制时交流功率分布的表达式为：

由上式可以看出，采用自注入APF控制策略后，电容电压上的波动产生了变化，电容输出功率的幅值和相位也随之产生了变化。并且由式（18）可以看出，电感电流上的波动将变为零。此时交流功率相量将发生变化，如图5所示。此时逆变桥输出功率的交流成分将完全由电容提供，同时和未进行电感电流纹波抑制时相比，电容输出的交流功率将变低。

由于二倍频功率在Quasi-Z源逆变器中反向流动造成Quasi-Z源网络输入功率的波动。区别基于反馈控制的纹波抑制策略，本文所提方案直接对扰动源进行了提取，经过处理后直接叠加至控制量，从本质上看是一种前馈控制，因而本方案具有良好的动态特性，可以在负载突变时快速响应。

3仿真分析

为验证纹波自注入式APF控制策略对Quasi-Z源逆变器输入电流纹波的抑制作用，运用MATLAB/Simulink搭建单相Quasi-Z源逆变器并网仿真模型，仿真参数如表1所示。

采用本文所提纹波控制策略和未采用纹波控制策略的Quasi-Z源网络输入电流i_L1（ι）如图8所示。可以看出，在未加入控制时，Quasi-Z源输入电流中明显含有二倍频纹波，加入所提控制策略后，输入电流交流成分明显减小。对比图9（a）和（b）可以看出，采用所提控制策略前后输入电流中的直流成分基本保持一致，同时其二倍频成分有效值由未控制前的1.753A降低到了0.03278A，说明此时输入侧电流波动得到了明显的抑制。图10所示的并网电流波形可以看出，采用所提控制策略后，并网电流没有较大变化，即逆变器输出功率并未产生变化。图11表示采用所提纹波控制前后直通占空比的波形，可以看出，采用所提控制策略后，直通占空比由一个恒定值变成了一个含有二倍频交流分量的变化值。图12所示为电容电压波形，采用所提控制策略后电容电压中交流分量幅值将低于未采用控制策略时。这与前一节的分析相一致，电感、电容、逆变桥、直流电源的瞬时交流功率均为相量，应满足图4和5的关系。因此采用自注入式APF控制策略后，可以一定程度上降低Quasi-Z源网络电容的应力。

由于纹波自注入式APF控制策略时利用前馈控制的思想，直接对造成Quasi-Z源网络工作不稳

4结论

本文将Quasi-Z源逆变器分为2个二端口网络建模后分析了二倍频能量传递机理，通过对Quasi-Z源网络模型分析得知通过改变直通占空比可以生成二倍频能量，以此为基础利用Quasi-Z源网络产生的二倍频能量与交流侧的二倍频能量相抵消，进而提出自注入式APF控制策略，对并网电流进行处理后得到逆变桥输出电流的交流分量，并通过控制器处理后将其叠加至用于升压控制的直通占空比上。通过仿真验证表明：所提控制策略可以将Quasi-Z源网络输入端纹波电流幅值降低81.4%，并具有良好的动态响应性能。