变负载空间机械臂混沌运动分析与控制

刘福才 闫莉莉 秦利 徐智颖

摘要：针对空间机械臂在轨服役时操作任务复杂多样且外部扰动随机等因素可能引起系统动力学特性和控制性能发生变化这一问题，研究了其负载不确定及外部扰动与重力释放的耦合影响引起的系统混沌运动，讨论了一种基于模糊幂次趋近律的快速滑模变结构控制方法。首先应用相图法、庞加莱映射法和最大李亚普诺夫指数法，分析系统在地面和空间两种环境的不同工况中，可能出现的混沌现象，及该情况下负载质量参数范围。通过对传统滑模面分析和比较，设计了一种快速非线性滑模面，根据模糊控制理论，设计模糊幂次趋近律，在实现混沌状态有效抑制的前提下，提高了系统的趋近运动速度。最后，通过与常规控制策略的对比仿真研究，验证了所提控制方案的有效性。

关键词：空间机械臂;重力效应;负载变化;混沌运动;滑模变结构控制

DOI：10.15938/j.emC.2019.10.014

中图分类号：TP 241;0322文献标志码：A 文章编号：1007-449X（2019）10-0120-09

0引言

空间机构服役于太空微重力环境，但其装配和调试过程是在地面环境完成的，太空环境的复杂和力学环境的变化会使其动力学特性和控制性能发生變化。清华大学利用悬吊技术研究了不同重力指向下可展开桁架机构的动力学响应，结果显示重力环境下机构运动更易趋于稳定。V.G6chshenko等通过分析大量试验数据发现微重力环境下，航天器机载电子设备会出现电池逻辑状态反转、逻辑元件开关容量异常等故障。重力效应对空间机构研发和应用过程运动行为的影响引起了学者们的关注，进而开展了空间机构服役性能地面模拟研究工作，如自由落体、飞机抛物线飞行、悬吊、气浮等模拟试验方法。目前仍面临地面任务级微重力模拟环境难以有效搭建的问题，如日本空间站机械臂系统精细臂样机的飞机抛物线试验结果显示其动力学特性以及控制力矩的变化规律与地面有很大不同。机械臂飞行演示实验（manipulator flightdemonstration，MFD）在轨飞行测试的试验结果表明其定位误差与地面悬吊模拟试验数据有明显差异。文献分析了重力对运动关节界面间隙及运动阻力的影响，提出采用运动行为模拟代替环境模拟、开展空间机构地面模拟研究的设想，为空间机构研究和探索提供了一种新思路。

太空环境变化复杂的非线性因素令空间机构的动力学特性对某些设计参数与操作工况的微小变化十分敏感，而限制了研发时机构运动行为的可预测性与实际应用中控制系统的稳定性，地面装调阶段容易掩盖实际多变的非结构化在轨操作中可能出现的混沌运动。如文献分析陀螺仪卫星的动力学行为，发现转子不对称会导致系统发生混沌运动。文献利用Melnikov数值方法分析了卫星在系统参数变化时发生的混沌运动。许多在理论模型中难以精确与充分表达的混沌运动特征不断被证实，相关研究一方面集中在对系统混沌现象的分析，如空间机构受重力梯度、系统结构不对称及参数变化、内外扰动等因素影响发生的混沌运动，相应结论可为机构设计提供理论基础;另一方面，针对应用场景广泛的空间操控机构，除了改进设计对一定范围的参数进行合理规避，具有混沌抑制能力的控制策略优化也受到重视。如文献设计递归比例反馈（RPF）和连续延迟反馈控制方法对绳系卫星在椭圆轨道和圆形轨道做俯仰、滚转运动时可能会出现混沌运动进行抑制。文献设计基于Lyapunov方法的自适应控制律对受扰航天器在系统参数变化时出现的混沌运动抑制。文献针对具有内部阻尼的磁性刚性航天器的混沌姿态运动，设计了输入输出反馈线性化方法进行抑制。每种控制策略都具备各自的特点与局限，且复杂空间机构的混沌抑制策略设计往往要针对各类机构的特殊性，有待进一步探索。

空间机械臂作为典型空间机构，在太空工作中具有不可替代的支撑作用。在轨任务中，机械臂操作对象未知，往往惯性参数变化较大，在地面难以实现其服役全生命周期各种工况的真实模拟。这对空间机械臂控制性能和操作精度提出了更高的要求，文献分析了负载转矩的变化对空间机器人伺服系统性能的影响，设计状态观测器，采用最小峰值方法自动调整调节器参数。文献针对空间机器人在轨燃料消耗，硬件重构，目标捕获等原因造成的惯性参数变化问题，根据非线性优化方法实现惯性参数识别，采用粒子群优化算法确定控制参数。重力释放与负载动量变化及外部干扰的耦合作用，可能会使空间机械臂系统在轨服役时发生混沌运动，造成操作任务的失败。如文献分析了受重力梯度扰动的自由漂浮空间机器人混沌姿态非线性动力学特性。文献针对空间自由浮动冗余机器人的混沌运动设计了自适应延迟反馈控制策略实现对其抑制。但并未分析空间机器人地面装调与空间应用不同阶段重力环境的变化对系统动态性能和控制器有效性的影响。文献考虑空间机械臂研发与应用阶段重力环境的变化，设计了对重力环境改变自适应的控制方案，但未涉及工况变化可能发生的混沌运动的抑制。

基于上述考虑，本文研究在不同重力环境下采用同一常规控制器时，负载不确定及外部扰动与重力释放的耦合影响使空间机械臂系统出现的混沌运动，并分析出使系统出现混沌运动的负载质量参数范围，进一步说明了空间机械臂服役全生命周期使用常规控制器时控制效果的局限性。然后，对空间机械臂新型滑模控制律进行设计，根据系统跟踪误差的大小，提出一种分段非线性快速滑模面设计方法，使机械臂系统控制收敛速度加快;针对机械臂混沌运动状态抑制问题，利用模糊理论，设计基于幂次趋近律的新型趋近律，以保证系统在不同负载质量下的关节跟踪效果。最终提出一种在不改变控制器结构与参数的情况下，可实现不同负载及外部扰动下机器人系统混沌运动自适应抑制与末端准确定位的控制方案。

1机械臂系统动力学模型

图2为负载质量较小，取m_p=50kg时地面调试以及空间应用阶段空间机械臂系统分别在τ_ground和τ_space控制下的末端轨迹跟踪曲线和误差曲线。

从图2所示仿真结果可以看出，当负载质量较小时，对地面和空间中三种不同机械臂动力学模型分别用基于式（6）的τ_ground和τ_space进行控制，使用同一控制参数，一定时间后均能实现对期望轨迹的跟踪。

进一步采用同样的控制器，在载体质量改变后，对空间机械臂在不同重力环境下操作不同负载的情况下进行轨迹跟踪控制，取负载质量由m_p=50kg增加为m_p=200kg，地面装调阶段、空间应用阶段自由漂浮基座和等价固定基座系统仿真结果如图3-图5所示。

图3为负载质量增加为m_p=200kg时，地面装调阶段机械臂关节2轨迹跟踪结果、空间相图和庞加莱截面图，可以看到，使用常规控制器仍能实现较好的控制效果，此时系统没有出现混沌运动。

图4为自由漂浮空间机械臂关节2的轨迹跟踪曲线、空间相图、庞加莱截面图及分叉图仿真结果，可见图4中的角位移轨迹跟踪效果较差，对系统初值敏感，空间相图轨迹在一定区域内随机分布、反复折叠，庞加莱截面图中的映射截点呈现为成片的离散密集点。根据wolf方法分别计算3种情况下系统动力学方程的关节2时间一位移序列的最大李雅普诺夫指数，分别为λ_maxl=3.0899>0，表明系统处于混沌运动状态。由图4（d）所示分叉图可知，系统在m_p>150kg时，会出现混沌现象。

对等价固定基空间机械臂系统进行轨迹跟踪控制，同样取负载质量增加为m_p=200kg，仿真结果如图5所示。

由图5所示机械臂關节2的轨迹跟踪曲线、空间相图以及Poincare截面图均可看出等价固定基空间机械臂系统处于混沌运动状态，计算关节2的最大李雅普诺夫指数λ_max4=6.5982>0。由图5（d）所示分叉图可以看出，系统在m_p∈[100kg，220kg]时会出现混沌。图6所示为操作负载变化较大时，不同重力环境下空间机械臂关节驱动力变化曲线，空间应用阶段发生混沌运动时，关节驱动力较大，不利于系统稳定。综上，采用常规控制器无法保证机械臂服役全生命周期的有效运行，也就说明在组合不同舱段后，机械臂的后续操作任务存在失败的可能性。

3模糊滑模变结构控制器设计

3.1快速滑模面设计

滑模变结构控制系统的运动分为趋近运动和滑动运动，当系统处于滑动运动时，对被控对象的模型误差、对象参数的变化以及外部干扰有极佳的不敏感性，鲁棒性较强。针对所研究空间机械臂系统，在快速终端滑模面的基础上，设计了一种基于状态变量x的新型快速分段滑模面，以提供状态的收敛速度，表示为：

设机械臂关节位置跟踪误差e为系统状态变量，即

其中：q为实际关节位置矢量，q_d为期望关节位置矢量。则机械臂滑模面设计为：

3.2趋近律设计

趋近运动阶段系统从任意初始状态趋向切换面，滑模可达性条件没有对这一运动阶段的具体轨迹作出规定，为保证趋近运动的品质，设计幂次趋近律，表示为

当系统状态接近滑模面时，趋近速度有所降低，有利于削弱振动，抑制混沌状态。当状态远离滑模面时，幂次趋近律速度过小，使趋近过程时间过长，进而影响系统的性能。则γ的值应综合考虑系统趋近速度和混沌状态两因素进行选取，采用模糊控制方法来确定幂次趋近律中γ的值。滑模面s是关于e的函数，通过s的值可间接估计干扰的大小。基于此，设计一维模糊控制器，通过|s|的大小，实时调整趋近律的参数γ。

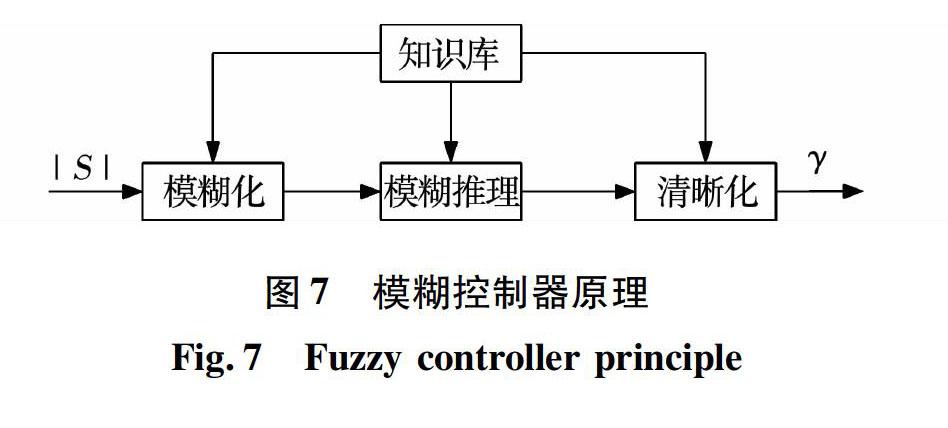
图7为模糊控制原理框图，|s|为模糊控制器输入变量，|s|为输出变量。用于表示输入变量和输出变量语言值的模糊子集均为{ZR，PS，PM，PB}。设输入变量|s|的论域为X，把|s|的大小量化为6个等级，即X={0，1，2，3，4，5};设输出变量γ的论域为Y，类似地，将γ的大小也量化成6个等级。

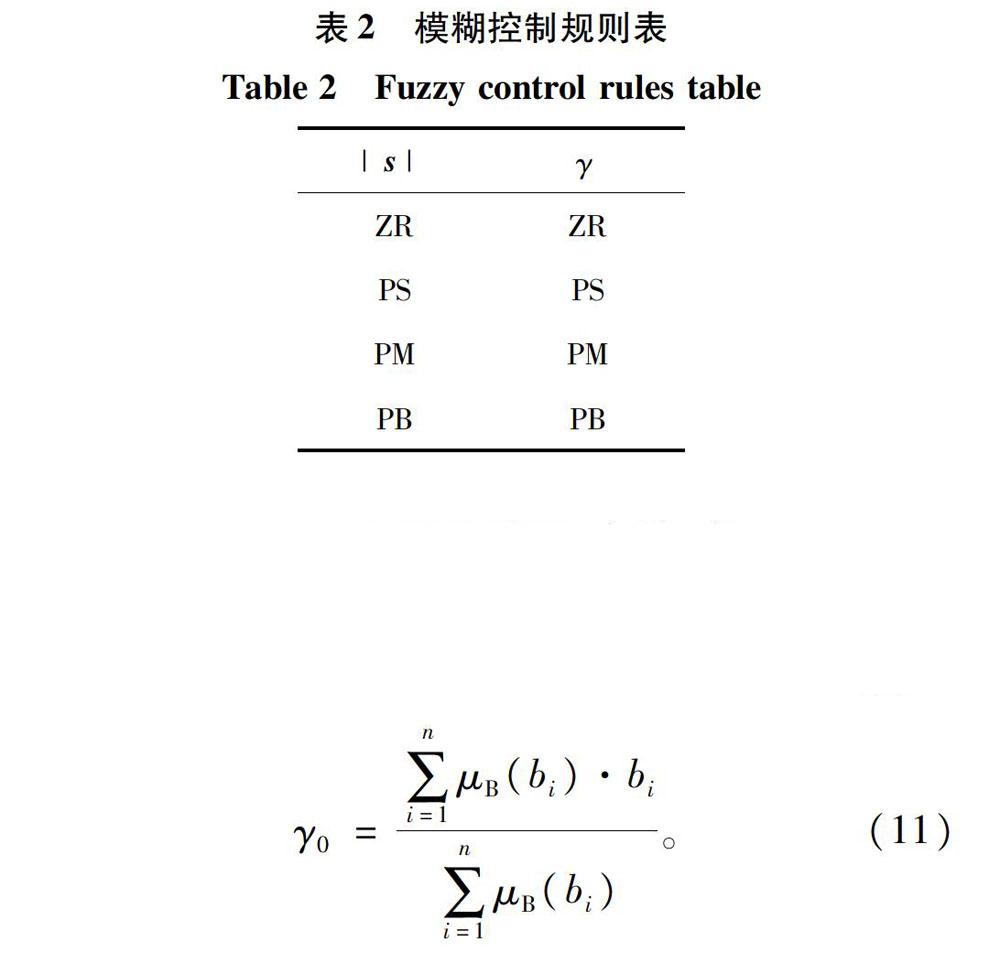
根据经验，当|s|为PB时，表示系统状态远离滑模面，此时γ须较大，也应为四，从而加快趋近速度;当|s|为PS时，表示系统状态接近滑模面，γ须较小，也应为PS，从而抑制混沌状态。基于此，可得表2所示模糊控制规则表。

选择MIN-MAX-GRAVITY方法对模糊量进行清晰化处理，可得清晰化的控制量γ_o。实际控制量γ可由γ_o经过尺度变换转化得到，γ_o表达式如下式中：μ_B（b_i）表示隶属度;b_i表示隶属度的自变量。引入双曲正切函数，将式（10）改写为

该趋近律的设计过程有效的避免了指数趋近律设计中滑模运动切换带呈带状的问题，同时保证了趋近速度。系统状态接近滑模面时，趋近速度已接近零，减小状态的偏离，有效抑制了混沌状态。

3.3控制器的设计

对式（9）进行求导，得到

3.4稳定性分析

采用上述模糊滑模变结构控制算法，可使系统的运动点能够从任意给定的初始状态e（0），在有限的时间内到达平衡点，最后趋于稳定。证明如下：

1）系统状态在有限时间内到达平衡点

根据所设计的新型快速分段滑模面，系统从初始状态到达平衡点的过程被分为|e|≥1和|e|<1两个阶段。以e≥0这种情况进行分析，e≤O证明过程相同，也就是分析从初始状态到e（t）=1和从e（t）=1到平衡点这两个阶段的性能。

（1）从初始状态到达e（t）=l

在这一阶段，e≥1。根据式（9），有对上式进行积分，得这一阶段所用时间

两阶段时间和即为系统从初始状态到平衡点所需的时间，即

t=t₁+t₂。（22）

综上，所设计滑模面可以再有限时间内到达平衡点。

2）稳定性分析

证明：在滑模面上，s=0，根据式（9）得到：

当系统状态到达并保持在滑模面上时，选取Lyapunov函数对式（25）求导，结合式（24），可得：

已知α>0，β>0，p，r均为正奇数，则满足：

根据Lyapunov稳定性原理可知，系统是渐近稳定的。

4仿真实验

为验证所提出的控制方案可以有效的抑制混沌运动，对地面调试以及空间应用阶段的不同工况下机械臂系统轨迹跟踪情况进行仿真研究，并与常规控制器的仿真结果进行比较。控制参数设置为：α=30，β=2，κ=90，r=9，p=7，系统扰动ω=[0.05

0.05]^T。仿真结果如图8所示。

图8所示为m_p=200kg时，采用所设计控制策略，地面调试与空间应用阶段机械臂系统仿真结果，可见，机械臂系统末端轨迹跟踪效果良好，计算3种情况下关节2位移-时间序列的最大李雅普诺夫指数分别为λ_max9=-0.7904<0、λ_max10=-0.1652<0、λ_max11=-0.5417<0，表明混沌运动得到有效的抑制，系统趋于稳定。图8（b）所示为空间和地面关节驱动力变化曲线，对比图6曲线可知，采用所设计的控制器，机械臂关节驱动力变小。

5结论

通过研究，验证了空间站长期建设过程中服役的空间机械臂随实际操作工况改变，可由重力以及负载惯性参数变化引起的混沌运动，并分析了可能造成混沌运动的操作负载质量范围。分析了地面装调和空间应用不同阶段的动力学特性，基于模糊幂次律的快速滑模控制理论所设计的控制方案对系统混沌运动状态的抑制有明显效果，且收敛速度更快，实现对不同工况混沌运动的自适应抑制与期望运动目标的跟踪，并对外界干扰和参数摄动具有一定的鲁棒性。