交直流输电线路离子流场的时域混合有限元法
2019-12-03田毅黄新波田文超曹雯朱永灿赵隆张烨
田毅 黄新波 田文超 曹雯 朱永灿 赵隆 张烨


摘要:高压交、直流输电线路同走廊架设作为一种提高走廊输电能力和节约土地资源的方法得到大力发展。两种线路相互接近时,其电磁环境与交直流线路单独运行时是不同的,因此需要对混合场进行分析从而指导混合线路的设计。在分析混合线路离子流场中,第一次将时域混合有限元法应用于混合离子流场的数值模拟。此外,在数值模拟中高压直流和交流输电线路之间的相互作用被考虑。通过与实测结果以及现有方法相比,证明了所提方法更加适合交、直流线路混合离子流场问题的分析,并且在提高计算效率和精确度的同时获得了无震荡数值解。对不同混合线路配置模型的地面电场和离子流密度进行了数值模拟,通过分析计算结果,总结了混合输电线路电场分布的一般规律。最后,利用所提数值模拟方法对两种典型的全尺寸同走廊输电线路模型进行了分析,进而为工程设计提供参考.
关键词:混合线路;离子流场;电晕;时域混合有限元法;电场分布
DOI:10.15938/j.emc.2019.10.010
中图分类号:TM 835文献标志码:A 文章编号:1007-449X(2019)10-0085-10
0引言
随着经济的发展,电力需求与日俱增,交直流混合输电线路作为一种提高同走廊长距离输电能力的手段,近几十年来得到了大力的发展。当交流线路和直流线路相互接近时,许多潜在的问题需要我们去确定。为了指导实际工程的设计和优化,并控制高电压铁塔周围电场分布以满足电磁环境标准,需要开发一种高精确度、高效的数值分析方法。
交直流混合离子流场的研究已经进行了多年。早期研究的重点主要集中在分析解决方法上,对于混合离子流场通常通过大量的假设条件来进行大幅简化从而便于数值计算分析。近年来,混合电场分布的数值分析方法得到了进一步的发展。杨勇等将ZHAO T等提出的单相单极性交直流电场的计算方法应用到三相双极性交直流电场的计算中。李伟和张波等提出了一种求解混合电场的时域迎风差分方法。尹晗等通过引入一步校正法和改进型算子分裂法改进了李伟等的工作。卢铁兵和周象贤等提出了一种基于有限元(finite elementmethod,FEM)和有限体积法(finite volume method,FVM)的新方法,其电荷注入由每一时间步迭代确定。这些方法,问题的计算准确性、效率和稳定性与节点数量之间的关系还存在非常大的问题,并且分析时域只达到一阶。
本文通过引入吸收边界条件对求解域进行了重新划分,基于时域混合有限元法对交直流混合离子流场进行数值分析。通过与现有方法以及实测结果的比较,验证了所提方法的高效性。此外,采用所提方法计算了4种混合线路模型的地面电场和离子流密度。通过比较这些数据,总结了交直流输电线路混合电场分布的一般规律。最后,对同走廊的两种典型全尺寸交直流混合输电线路的离子流场进行了分析和预测。
1计算模型
当直流线路靠近交流线路时,其混合离子流场既不属于静态问题,也不是两种离子流场简单的线性叠加,而变成了一种非常复杂的时变动态混合离子流场。
1.1控制方程
交直流输电线路混合系统的电晕是一种依赖时间的双极性离子流场问题,其控制方程如下
1.2求解域划分
简化的线路模型包括一系列的圆柱形无限长导线,它们之间相互平行的位于地平面上。三维传输线可以遵循这个简化模型,使用一个二维模型来表示:即垂直于平面的导线。时域分析方法被采用,在每一时间步长,由于交流线路的存在离子运动将变得更加复杂,且离子复合及离子约束变得更加明显。求解域Ω是二维域上的一个有界凸多边形,其边界T代表边界集合,根据离子的运动方向其被划分如下:
1.3边界条件
离子流场的数值方程是超一阶非线性偏微分方程。对于泊松方程,导线的电势和地平面是给定的,需要通过添加人工边界使其求解域变为有界。对于电流连续方程,导线边界的电场和电荷密度被设置为边界条件。如Streamline upwind/Petrov-Galerkin方程所示,迎风单元的加权余量形式有效地将较重的权重加权在上流节点上而非下流节点。如果电势梯度不是很大,则上流节点和下流节点值之间的差異很小,加权余量则对权函数的形状不是很敏感。因此是否使用迎风方案或网格细化来避免数值震荡,不应该由对流占优方程的形式决定,而是应该基于边界层存在形式即其形成的机制,其通常是由边界条件类型来控制。通过上面的分析,在边界条件上采用吸收边界条件。合适的人工边界选择,可以使人射波的反射最小。
根据Kaptzov条件,放电极的表面电场保持起始值。当导线电晕时,流入边界上的离子密度被初始化,而在其他时刻其被设置为零;在流出边界上离子被吸收,然后该部分的离子密度被取消。
1.4泊松方程的求解
泊松方程控制空间电荷存在下的电势分布,其通过混合有限元法求解。为了便于计算,将二阶泊松方程分解为两个一阶方程,因此如下矢通量函数被引入
为了数值计算混合有限元,在内部单元边界上引入拉格朗日乘数λ∈L2(Fh),从而自动满足边界条件,同时内部单元边沿之间的连续性被放松。即:
注意:
(1)拉格朗日乘数的引入,第三个方程规定了空间电荷在速度场上所需的连续性。式(13)中μ∈L2(Fh)也为拉格朗日乘数并与λ等价。λ是ψ(t)在内部单元边界上的轨迹,其满足
λ(s)=ψ(s) on Fh。(14)
(2)Ω项增强了单元域上对流占优方程的满足度。为了提高精确度,采用α最优六阶三角形单元离散。每个内部计算域采用标准Galerkin方法处理。
(3)为了表示相邻单元接口间的关系,混合有限元法引入了跳跃算子,其定义如下
1.5电流连续性方程的求解
在空间域和时间维度对电流连续方程进行离散化。为了获得较好的精确度,在空间域采用间断有限元法,在时域应用三阶显示总变差减小龙格库塔法(total variation diminishing Runge-Kutta,TVDRK3)。将式(2)代入式(4)中,然后对其和式(3)分别乘以基函数Wh∈Vh,并在计算域内分别进行积分。对于积分后的方程分别利用间断有限元法计算,放松内部单元间的边界连续性,从而推导出电流连续方程的间断有限元形式,即:
1.6求解过程
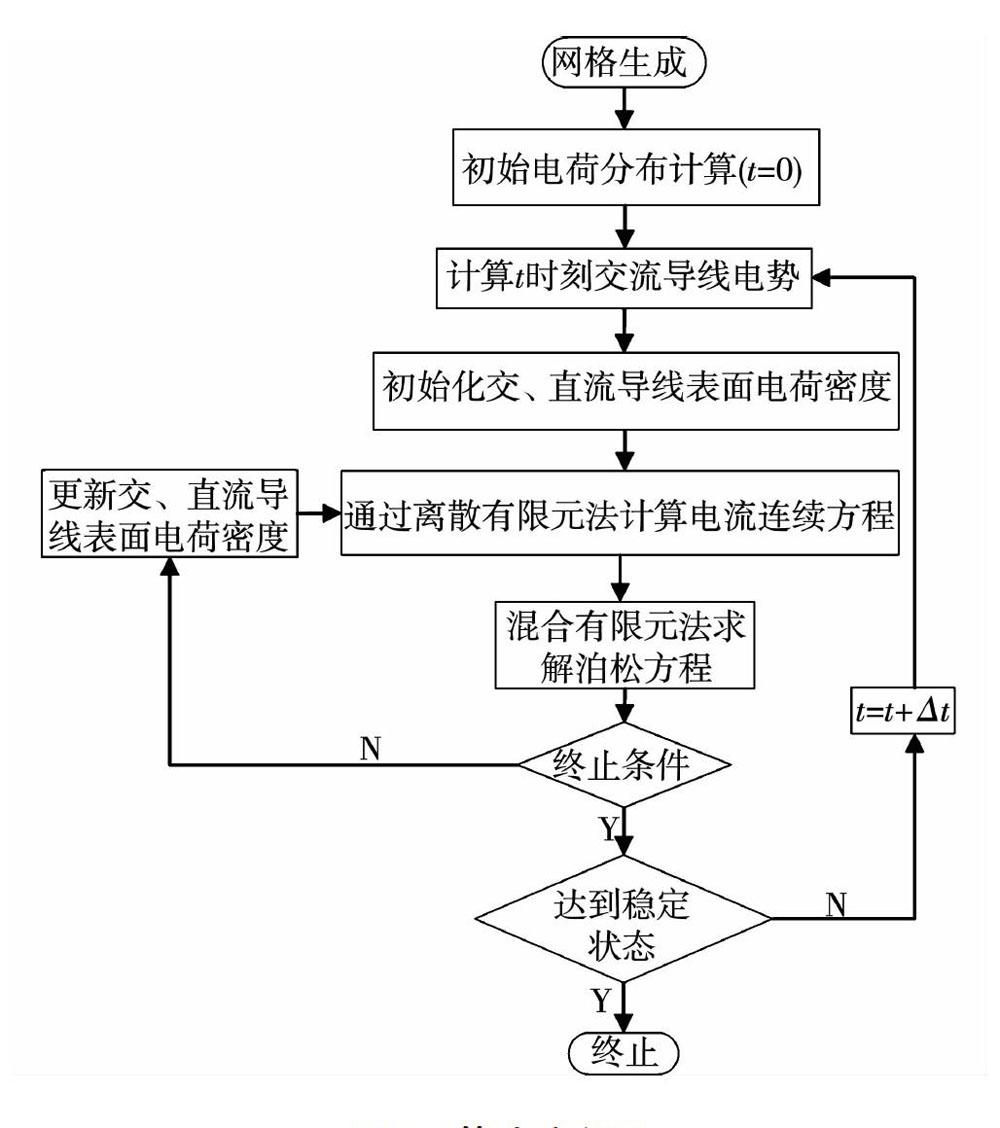
交直流混合离子流场为电场-空间电荷耦合问题,因此其数值分析为非线性过程,其是通过迭代求解泊松方程和电流连续方程来实现的。根据上文的分析,提出了一种基于时域的新算法,其计算过程如图l所示。导线表面起晕场强作为边界条件,这样整个计算满足Kaptzov假设。在内层循环,如果满足电荷密度δρ和电位δρ的相对误差,则计算结束,否则修正导线表面电荷密度。
在外层时间循环,用显示了VD RK3在时域计算电流连续方程,分别单独迭代求解正、负空间电荷。不断循环计算整个外层循环直到过去两个计算周期的计算结果近似时终止。
1.7所提方法的优点
在求解离子流场问题时,严重的震荡通常是由于顺风边界变量变化迅速而导致。这里的震荡代表伪数值解,其主要是由于在计算域的边界采用了不合适的有限元网格划分。因此,为了消除计算结构的数值震荡,采用吸收边界层类型来消除震荡。
为了消除沿轨迹逼近驻点的震荡,有限元法和有限体积法的Peclet数必须满足如下限制
通过观察公式(33),我们发现网格必须非常小才能使得扩散系数D在敏感区域足够的小,因此就要求计算网格必须非常的细化。表1总结了所提方法与有限元法及有限体积法的对比。
在空间离散上所提方法采用与FEM相同阶数的单元形函数,但是其系统系数矩阵更加稀疏,从而带来更快的求解过程;在方程的边界上通过添加数学算子来实现内部单元边界的离散,从而保证计算网格在计算域是连续的;在不改变网格数量的前提下通过采用α优化节点集和多阶多项式基极大的提高了计算精确度。在时域离散上通过采用更大的稳定时间步长来抵消额外增加的一步计算。因此,与FEM和FVM相比较,所提方法的计算效率有了极大的提高。同时采用迭代方法而不是牛顿法,这样的好处是避免了多阶导数的求解从而减小了整个计算的复杂度,同时提高了计算效率。时域方法更加深入地分析了研究对象的物理特性。
2计算方法有效性验证
前文已经在理论上分析了所提方法的可行性,并且與已有的方法进行了对比。为了进一步验证所提数值方法,研究了文献中提出的一种缩小规模的交直流混合线路模型,如图2所示。对于图2中的模型,电晕仅发生在直流导线上;根据上文的定义将整个计算区域划分为矩形区域,其以交、直流导线中心为中心,距离左右边界距离相等,即为3.7m,上边界距离地面高度为4.4m,下边界为地面。
单相交流和单/双极性直流线路的地面电场和离子流密度分别被计算,计算结果如图2所示,其中“实验测试结果”为文献中EPRI实验长期测试值。通过观察图2发现所提方法计算出的结果非常接近实验测试值。针对上述典型的缩小规模交直流混合线路,所提方法与FEM、FVM的计算时间进行了对比,如表2所示。从表2中可以看出,所提方法比FEM和FVM的计算效率更高,特别是在高精确度的情况下。
图2中,由于交流导线未起晕,因此交流导线通电时的地面电场和离子流密度与交流导线接地时非常接近。这与后文中交流线路电晕时的情况形成了巨大的反差。这主要是由于混合场中交流线路的屏蔽作用,而交流线路的屏蔽作用包括两方面:离子中和效应的增加及交流电场对直流导线电晕产生的空间电荷运动的改变,而这里的根本原因是由于交流导线没有发生电晕从而其对于离子的中和效应不存在。另外,所提方法考虑了交流导线对直流导线表面电场的影响,因此其导线表面电场呈现出周期性变化,但是其导线表面的总电场依然满足Kaptzov假设。
3交直流混合离子流场分析
为了进一步研究交直流混合离子流场和探索其一般规律,对4种不同形式的混合线路模型进行了研究,其几何尺寸如图3所示。对于每一种单相交流和双极性直流线路混合模型,其每条线路均包含两条外径相同的导线束,直流电压和交流电压的有效值分别为±40kV和28kV。
利用所提的方法对4类混合线路模型的地面电场和离子流密度分别进行计算,计算结果如图4和图5所示。通过比较这些数据,对混合线路模型电场分布的一般规律总结如下:
(1)随着直流导线位置的变高,合成电场强度的最大值逐渐变小。同时当交流线路位于直流线路和地平面之间时,电场强度将显著减小,其减小的原因主要为交流导线的屏蔽效应。
(2)当交流导线位于直流导线的上方或一侧时,交流导线施加电压的大小对于整个电场分布和离子流密度的影响非常小。
(3)当交流导线位于直流导线下方时,交流导线上施加电压的幅值对混合电场分布有较大的影响。当交流导线的电压低于电晕起始电压时,其对于整个电场分布的影响很小;而当交流导线的电压大于电晕起始电压时,电场强度的幅值变小以及整个电场分布曲线向负半轴移动。
(4)在相同幅值的导线电压下,负极性电晕强于正极性电晕,在图中表现为负半轴电场曲线和离子流密度曲线的最大值大于正半轴的。
(5)当负极性(或正极性)导线位于正极性(或负极性)下方时,电场曲线和离子流密度曲线轮廓的大部分位于负半轴侧(或正半轴侧)。
(6)在一般情况下,离子流密度与电场强度曲线具有相同的趋势。
4应用
同走廊全尺寸混合输电线路主要包括两种混合线路模型:交流和直流线路分别位于相邻的两级杆塔上如图6(a)所示;标准的双回路交流线路系统中一回路被直流线路代替如图7(a)所示。两种模型直流电压为±800kV,交流电压有效值为500kV,利用所提的方法对其进行对比分析研究。该混合线路模型的交直流导线分别采用如下规格:分裂间距为40cm的6×LGJ-500/35型导线和分裂间距为45cm的6×ACSR-720/50型导线;地线分别采用:JLB1A-185和JLB1A-150型导线。
分别计算两种混合线路模型的地面电场和离子流密度,计算结果如图6和7所示。对比计算结果可以发现,同塔混合线路模型的地面电场和离子流密度的最大值较并行混合线路模型分别减少了40%和36%,但是对比图6(a)和7(a),我们发现对于同塔混合线路模型杆塔的横向较并行混合线路模型大了将近一倍。因此实际中采用哪种混合线路模型要根据具体的情况来决定。
5结论
对于高压交直流输电线路的混合离子流场的数值分析技术已经研究了许多年。本文的目标是开发一种新的模拟计算方法从而达到降低计算成本、提高精确度和稳定性的目的。因此,泊松方程通过混合有限元法求解,电流连续性方程在空间域通过离散有限元法求解,在时域通过显示TVD RK3方法求解。通过与现有的方法相比,本文发展的新方法实现了这一目标。
通过与缩小规模混合线路模型的实验测试结果相比较,证明了本文所提方法的有效性。通过计算不同配置的交直流混合场的地面电场和离子流密度分布,总结了其一般规律,并推导出最优的混合线路配置,从而为全尺寸混合输电线路的设计提供了理论依据。分析典型的两种全尺寸混合线路模型,从而得出同塔混合线路模型的地面电场强度和离子流密度的最大值较并行混合线路模型分别减少了40%和36%,但是同塔混合线路模型杆塔的横向较并行混合线路模型大了将近一倍。因此实际中采用哪种混合线路模型要根据具体的地理环境来确定。
