基于RLWE 支持身份隐私保护的双向认证密钥协商协议

杨亚涛，韩新光，黄洁润，赵阳

（1.西安电子科技大学通信工程学院，陕西 西安 710071；2.北京电子科技学院电子与通信工程系，北京 100070）

1 引言

密钥交换协议（key exchange protocol）[1]能够使通信双方或者多方在复杂信道上安全通信。1976年，Diffie 和 Hellman 设计了经典的Diffie-Hellman 密钥交换协议[2]，密钥协商需要两轮消息传输，此协议无法抵抗敌手发起的中间人攻击和重放攻击等，同时也不能提供相互认证的功能。

2001年，Li 等[3]提出适用于多服务环境的身份验证协议，这个解决方案导致通信成本和计算成本太高，不能适用于实际情况。2012年，Liu等[4]提出了一个基于离散对数问题的多服务器认证协议。2004年，Tsaur 等[5]提出了一种基于RSA 算法和大整数问题的多服务器协议。同年，Juang[6]提出另一种使用对称加密来验证身份的多服务器身份验证协议。然而，Chang 等[7]表明Juang 的协议易受离线字典攻击，因此提出了一个克服Juang 的协议安全漏洞的方案。2009年，Regev 等[8]提出了带错误的学习（LWE,learning with error）问题，说明了格上的最短向量问题等。2009年，Liao 等[9]提出了一种多服务器场景下的认证协议。2010年，Wu 等[10]提出了基于用户认证的密钥交换协议，该协议可以抵抗重放和密钥复制等攻击，并保证部分前向安全。Yoon等[11]引入了另一个基于客户端/服务器的用户认证密钥交换协议来提高性能。2010年，Lyubashevsky 等[12]引入环上带误差学习（RLWE,ring learning with error）问题，困难性基于理想格上的最短向量问题（SVP,shortest vector problem）。2011年，He 等[13]提出了椭圆曲线上的用户认证和密钥交换协议，该协议提供了远程相互认证与密钥协商，并可抵御各种已知的攻击。然而，Islam 等[14]证明了He 等[13]的协议易受已知密钥会话临时攻击、冒充攻击，无法保证用户的匿名性。2010年，Hao 等[15]提出了一个基于客户/服务器模型的PAKE（password authenticated key exchange）协议，该协议的安全性基于离散对数的困难性，这很容易受到量子计算机的攻击。2015年，Zhang 等[16]提出了一种新的基于格理论的认证与密钥交换方案。但是，他们需要参与者公钥/私钥对来完成身份认证。文献[17]提出了一隐私保护的会话密钥协商方法。文献[18]提出了一种身份隐藏且非延展安全的认证密钥协商方法。2016年，文献[19]提出了基于 LWE 的2PAKE 协议。文献[20]提出了关于验证元的三方口令认证密钥交换协议，但是存在效率低、占用资源多等缺点。2016年，Tseng 等[21]提出了用户身份验证和基于身份的密码系统的密钥协商协议，该协议能够抵抗移动多服务器中的随机数泄露攻击。2018年，Wu 等[22]提出了一种新的基于混沌映射的多服务器环境用户匿名认证密钥协商方案，不能抵抗量子计算机的攻击。同年，Sharma 等[23]提出了一种无配对的认证密钥协商协议，计算成本低，特别是对于低功率设备，但是存在长期密钥泄露和短暂密钥泄露的风险。2017年，Jheng 等[24]提出了一种基于格理论的客户端/服务器端模型的口令认证密钥协商协议，该协议通过共享口令完成相互认证密钥协商，但该协议用户的身份信息不具有匿名性且不能抵抗中间人攻击。

本文设计了一种基于RLWE 支持身份隐私保护的认证密钥协商协议。该协议通过C 类承诺机制的设计，将通信双方不愿暴露的真实身份信息隐藏为承诺值的形式，承诺值消息具有完整性，不可篡改。协议基于RLWE 困难问题，在保障身份匿名的前提下，通过2轮的消息交互不仅完成了双向身份认证，而且保证传输消息的完整性，并协商出共享会话密钥。通过分析，在协议执行效率上，完成匿名的双向认证与密钥协商只需经过2轮的消息传输，公钥长度较短。在安全性上，所提协议能够抵抗伪造攻击、重放攻击、密钥复制攻击和中间人攻击。在eCK 模型下满足可证明安全性，可以抵抗量子计算攻击。

2 基础知识

2.1 格

简单地说，格（lattice）是实数空间中线性无关向量的整系数组合的集合。可以形式化地描述为给定n个m维的线性无关的向量b1,b2,…,bn∈Rm×n，由它们作为基形成的格是由下列向量组成的集合，如式(1)所示。

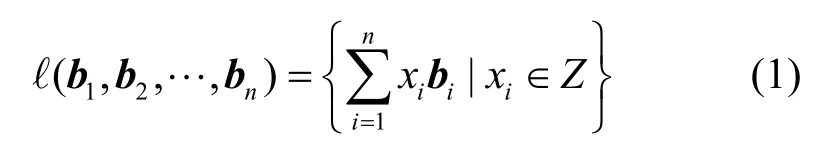
其中，b1,b2,…,bn为格的一组基，记为B=[b1,b2,…,bn]∈Rm×n。

2.2 RLWE 问题

定义1搜索性 RLWE 问题。令a均匀随机选取，e∈R是服从正态分布ψ的差错向量，若己知b∈R，且b=as+e，则由a、b求解s的问题就是搜索性RLWE 问题。

定义2判定性 RLWE 问题。令s均匀随机选取，e∈R是服从正态分布ψα的差错向量，计算b=as+e，且b∈R。记As,ψ为(a,b)的分布，则如何区分As,ψ与R×R上的均匀分布问题就是判定性RLWE 问题。假设判定性RLWE 问题是困难的，则As,ψ伪随机。

2.3 eCK 模型

定义3假设会话是新鲜的，则满足以下条件。

1)敌手E未对通信方i,j进行Ephemeral_Secret Reveal()和Static_Key Reveal()查询。

这里假设敌手E 能够任意伪造、重放和删除通信信息，是一个概率多项式时间的图灵机，且可完成以下功能。

1)Establish_Party(i)。敌手E 可在CA 上注册参与者i的公钥。

2)Ephemeral_Secret Reveal(i)。敌手E 获得i的临时私钥。

5)Static_Key Reveal(i)。敌手E 获得i的长期私钥。

2.4 C 类承诺机制

G是阶为q的群，q是素数，N是群G的生成元[25]。承诺时期，承诺者承诺被隐藏信息a∈{0,1,2,…,q-1}，计算com()=Na，将com()函数值发送给接收者。打开承诺，承诺者发送a给接收者，接收者证实等式com()=Na。

3 协议设计

3.1 协议参数选取

假设n是2的整数次幂，pw 是Alice 和Bob 的共享口令，G是阶为q的群，q是素数，N是群G的生成元。素数q满足q＞8且qm od2n=1，Rq是模数为q的多项式环，且，X是在Rq上的高斯离散分布，g是双方共享的公共参数，(pk,sk)是Bob 的公钥/私钥对，IDA和IDB是Alice和 Bob 的身份信息，协议中的 com 函数为com()=NH(ID)。协议中涉及的散列函数H使用SHA256算法，输出256 bit 的消息摘要。

3.2 协议执行流程

协议的执行流程如图1所示，具体如下。

1)Alice 随机选择y1∈(1,2,···,q)，计算u1=y1+H(IDA)，Alice 的身份信息IDA经过com()函数处理得到承诺值MA。Alice 选取参数fA,α,Nonce ←χ，利用fA,α生成认证参数X=gα+2fA，随后利用Bob 的公钥pk 加密得到Alice 的身份认证信息AuthA，之后将H(IDA)|X|AuthA|u1发送给Bob。

2)Bob 接收到H(IDA)|X|AuthA|u1后进行以下操作。

① Bob 接收到数据u1|H(IDA)，首先验证消息y1|u1|MA的完整性。Bob 计算。验证是否成立，如果等式成立，证明消息传送过程中，参数未被更改，消息具有完整性；反之，则消息验证失败，Bob 拒绝通信。

② Bob 收到AuthA后，利用自己的私钥sk 解密得到散列值HA=H(X|MA|pw|Nonce)和随机参数Nonce。Bob 利用参数X|MA|pw|Nonce，首先计算HB=H(X|MA|pw|Nonce)，若HB=HA，则Alice 的身份认证通过；反之失败，Bob 拒绝通信。若身份认证成功，Bob 随后选取参数fB,β,rB←χ得到认证参数Y=gβ+2fB，KB=Xβ+2rB。利用Sig 和 Extr 函数得到wB=Sig(KB)，ρB=Extr(KB,wB)。

图1 协议流程

③Bob 将身份信息IDB经com()函数处理得到承诺值MB，随机选择y2∈(1,2,···,q)，计算u2=y2+H(IDs)和 Bob 的身份认证信息AuthB=HB′(Y|MB|pw|wB|Nonce +1)，随后将H(IDB)|Y|AuthA|u2|wB发送给Alice。

最终 Bob 获得共享会话密钥skB=H(MA|MB|X|Y|wB|Nonce|ρB)。

3)Alice 接收到H(IDB)|Y|AuthA|u2|wB后进行以下操作。

①Alice 接收到Bob 传来的数据u2|H(IDB)，首先验证消息y2|u2|MB的完整性。Alice 计算并验证是否成立。若等式成立，证明消息传递途中参数y2|u2|MB没有被更改，消息具有完整性。反之，消息验证失败，Alice 拒绝通信。

②Alice 利用参数Y|MB|wB，将Nonce +1计算。若等式成立，Bob 的身份认证成功。反之失败，Alice 拒绝通信。若身份认证成功，Alice 随机选取参数rA←χ，计算KA=Yα+2rA，利用Extr 函数得到参数ρA=Extr(KA,wB)，则Bob 的共享会话密钥skA=H(MA|MB|X|Y|wB|Nonce|ρA)。共享会话密钥skA=skB，完成密钥协商。

3.3 协议的正确性证明

假设q是大于2的素数，，信号函数Sig(x)可定义为

证明假设q是大于8的奇数，则Extr 函数[26]定义为

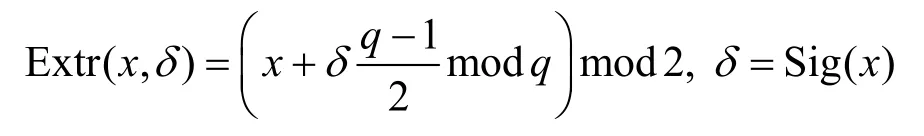
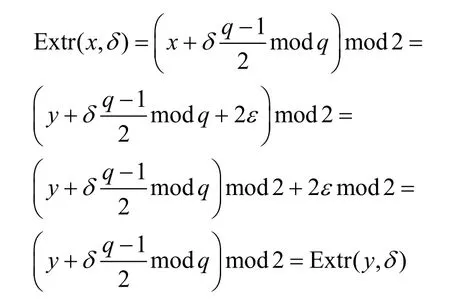
证毕。

3.4 协议的安全性证明

定义4敌手E 获胜的优势可定义为

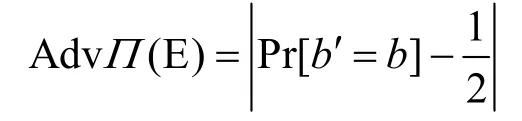
协议安全性条件介绍如下。

1)敌手E 可在匹配会话中获得相等的会话密钥。

2)在随机多项式时间内，敌手E 取得游戏胜利的概率忽略不计。

定理1在多项式时间内，若敌手E 在游戏中以不可忽略的概率获胜，则存在模拟器Q，能够以AdvΠ(Q)优势在以上时间内解决最短向量困难问题。

证明协议的安全性证明可归约到求解基于格上最短向量困难的问题上。假设敌手E 攻击协议成功，则证明敌手可以解决格上的最短向量困难问题。由于协议中会话密钥与随机数的不可区分性，敌手E 在协议运行多次的情形下，选择单次目标会话，从密钥空间中的随机数或真实的会话密钥之间随机获得一个，协议的安全性基于敌手E 仅以可忽略的概率分辨真实的会话密钥和密钥空间中的随机值。

1)密钥复制攻击

敌手E 与通信双方创建一个与测试会话拥有一致会话密钥的会话，协议中会话密钥的产生所依赖的参数fA,fB,α,Nonce,rB,rA随机选取，则证明在不同随机参数的输入情形下产生相同的会话密钥的概率可忽略。敌手E 在eCK 模型下不允许对同一通信参与者进行Static_Key Reveal()和Ephemeral_Secret Reveal()的同步查询，因此真实会话与攻击会话中同时拥有相同的认证密钥和相同随机数的事件发生的概率可忽略，协议可抵抗密钥复制攻击。

2)伪造攻击

敌手E 计算得到ρA,ρB，借助随机预言机获得会话密钥skA=H(MA|MB|X|Y|wB|Nonce|ρA)。假设敌手E 通过模拟器Q 的随机选取获得的n次会话中包括m次匹配会话，则模拟器Q 在通信双方Alice 和 Bob 之间获得匹配会话的概率为。如果敌手E 以概率p获得匹配会话，且敌手E 成功地获得了会话密钥skA，说明敌手E 可计算ρA,ρB，由于ρA=SVP (kA,wA)，ρB=SVP (kB,wB),说明模拟器Q 能够攻克格上的最短向量问题。敌手E 在eCK 模型下不能对同一参与者完成Static_Key Reveal()和Ephemeral_ Secret Reveal()的同步查询，而且随机预言机随机选取相同输入的情况可忽略，敌手E 和模拟器Q 的关系为

假设敌手E 能够在多项式时间内，利用n次会话中的m次匹配会话，并且在游戏中以优势AdvΠ(Q)获胜，证明模拟器Q 可在多项式时间内以优势AdvΠ(Q)攻克SVP，并满足AdvΠ(Q)≥，则协议可抵抗伪造攻击得证。

3)抵抗重放攻击

重放攻击即攻击者通过二次发送复制信息欺骗通信参与者的行为。协议中，Alice 每次随机选取参数fA,α,Nonce,rA，计算X,KA,ρA；Bob 每次随机选取参数fB,β,rB，计算Y,wB,ρB。使当前单次会话生成的认证函数值AuthA,AuthB不同，导致最终产生的会话密钥skA,skB不可匹配，表明协议可抵抗消息的重放攻击。

4)抵抗中间人攻击

中间人攻击可通过获取通信双方的通信信息，进行篡改和窃听的攻击行为。Bob 接收到数据u1|H(IDA)，首先验证消息y1|u1|MA的完整性。计算验证Nu1=dAMA是否成立，若成立，则证明通信过程中消息y1|u1|MA完整没有被更改。同理，Alice接收到Bob 传来的数据u2|H(IDB)，首先验证消息y2|u2|MB的完整性。Alice 计算y2=u2-H(IDB)，，并验证是否成立，若成立，则证明通信过程中消息完整，y2|u2|MB没有被更改。在这2次验证消息完整性的过程中，由于仅传输双方双份身份信息的摘要值H(IDA)|H(IDB)和经过处理的参数u1|u2，并不能获得参数y1|y2和MA|MB，则中间人无法对中的任意一项进行篡改并最终使等式成立，故此协议可抵抗中间人攻击。

证毕。

4 性能分析

为了证明本文方案的优势，将其与其他经典方案进行性能对比分析，如表1所示。文献[27]是LWE问题上的2PAKE 协议，不满足客户和服务端的双向认证，易受不可测字典攻击，消息传输3轮。文献[16]是RLWE 困难问题上的2PAKE 协议，消息传输2轮，用户无法匿名。以上2种方案公钥长度均为(2n+1)lgq。文献[28]设计了隐式和显式认证2类2PAKE 协议，公钥长度为2nlgq，消息传输轮数分别为2轮和3轮，用户无法匿名。文献[29]困难假设基于ASPH 困难问题，用户无法匿名，公钥长度为(2n+1)lgq，且需要4轮通信，消息传输轮数最多。文献[30]提出了一种基于格的三方认证密钥协商协议，困难假设基于RLWE 问题，用户具有匿名性，可抵抗不可测字典攻击，消息传输轮数为3轮，公钥长度为2nlgq。文献[24]提出了一种基于格理论的客户端/服务器端模型下口令认证密钥协商协议，用户不具有匿名性，消息传输需要2轮，公钥长度为nlgq，可抵抗不可测字典攻击，消息不具备完整性验证。本文方案公钥长度为nlgq，在实现用户匿名性的前提下与以上方案相比公钥长度最短，消息传输轮数少，仅需要2轮通信，且能抵抗中间人攻击、不可测字典攻击、密钥复制攻击、重放攻击、伪造和量子攻击。通过与Ding 等[28]的协议对比，本文方案公钥长度缩短50%，且消息传输轮数仅需要2轮，具有更好的安全性和通信性能。

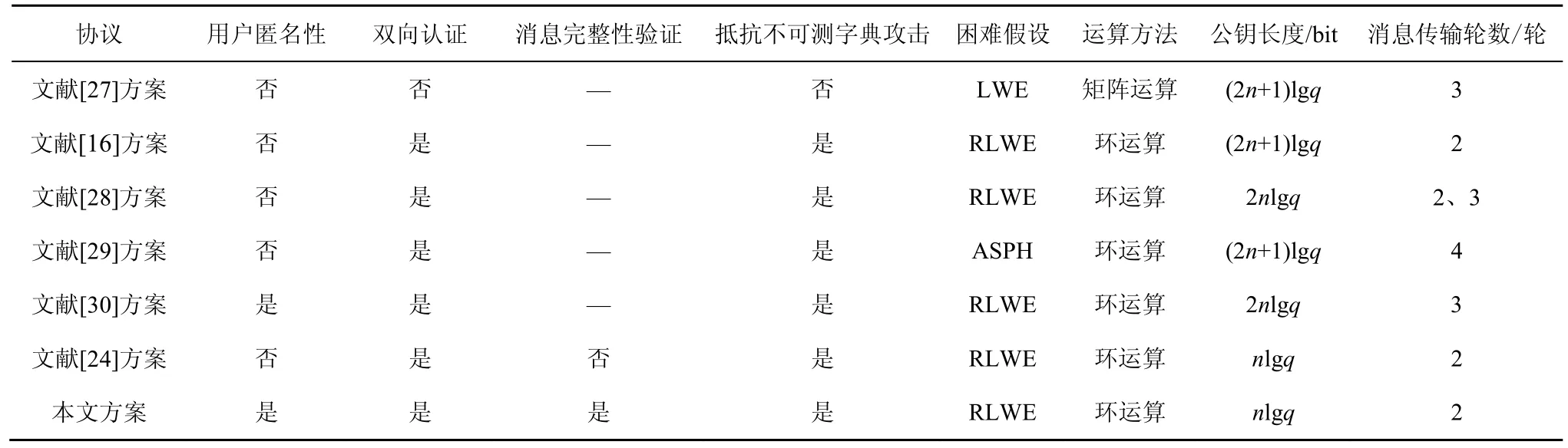
表1 协议性能对比分析

5 结束语

认证密钥交换协议可以在不安全的信道上协商出共同的会话密钥。为了解决执行认证密钥交换协议时通信双方身份匿名问题，本文提出了一种基于C 类承诺机制的抗量子攻击的双向认证密钥协商协议。该协议通过C 类承诺机制的设计，将通信双方不愿暴露的真实身份信息隐藏为承诺值的形式。协议基于RLWE 困难问题，在保障身份匿名的前提下，通过2轮的消息交互不仅完成了双向身份认证，而且保证传输消息的完整性，并协商出共享会话密钥。通过分析，在协议执行效率上，完成匿名的双向认证与密钥协商只需经过2轮的消息传输，公钥长度较短。本文协议满足可证明安全，可抵抗量子攻击。下一步研究计划将把本文协议进行软件快速实现。