基于特征值的频谱感知融合算法
2019-12-03赵文静李贺金明录
赵文静,李贺,金明录
(大连理工大学信息与通信工程学院,辽宁 大连 116024)
1 引言
随着无线宽带和多媒体用户市场的迅速扩大以及高数据速率的应用,频谱资源匮乏给未来的无线通信网络(5G 甚至是6G)带来很大挑战。未来的无线通信要给更多的用户提供更快更好的通信服务质量,满足这些要求的一个限制来自目前固定的频谱分配策略导致可用频率资源使用效率低[1-4]。提高频谱资源的使用效率是未来无线通信亟需解决的问题,为此,5G 使用的频谱范围将进一步扩展到毫米波频段,并采用动态频谱共享技术,即认知无线电(CR,cognitive radio)技术解决频谱匮乏的问题[5]。认知无线电的基本概念是频谱复用或频谱共享,它允许认知网络/认知用户(次用户)在主用户没有充分利用频谱的情况下,通过分配/许可给主用户的频谱进行通信。为此,需要认知用户频繁地进行频谱感知,即检测主用户的存在。当主用户处于激活状态时,认知用户必须以较高的概率检测到主用户的存在,并在一定的时间内清空信道或降低传输功率。然而,错综复杂的实际场景给频谱感知带来了很大的挑战,也促进了认知无线电技术的不断发展。
认知无线电技术一直受到学术界及工业界的广泛关注,大量的研究工作集中在设计可靠准确、高效的频谱感知技术[6-9]。根据不同的实现条件及要求,频谱感知算法分为最优检测算法、半盲检测算法和盲检测算法。匹配滤波算法是最优的频谱感知算法之一,其能够在次用户已知主用户信号和噪声信息的前提下取得最优的检测性能,且每个次用户均满足同步条件,这在实际场景中是难以实现的[10]。半盲检测算法是只需已知噪声功率的检测算法。典型的半盲检测算法有能量检测(ED,energy detection)[11],其不需要主用户的先验信息且易于实现,但是在实际情况中,因多径衰落及遮蔽现象导致信号功率波动,信噪比较低,使能量检测算法的性能严重下降。为此,文献[12]提出了一种基于历史信道状态信息的能量检测算法,其在检测性能上有一定的提升。ED 算法对于独立同分布信号具有最优的检测性能,而对于相关信号的检测性能相对较低。ED 算法需要已知噪声功率,然而,实际系统中噪声随时间变化,存在噪声不确定性问题,这导致“信噪比墙”的产生和虚警概率的升高。为了克服这些缺点,全盲检测算法应运而生,这类算法既不需要信号功率信息也不需要噪声功率信息。基于特征值的检测算法是一类典型的全盲检测算法,其利用了接收信号的样本协方差矩阵捕捉信号间的相关性,很大程度上提高了对主用户的感知能力,这引发了一些基于特征值检测算法的提出[13-14]。例如最大最小特征值(MME,maximum-minimum eigenvalue)算法[15]、最大特征值与迹(MET,maximum eigenvalue-trace)算法[16-17]、最大特征值与特征值的几何平均(MEGM,maximum eigenvalue to the geometric mean)算法[18]和极特征值的均方比(MSEE,mean-to-square extreme eigenvalue)算法[19]等。
在低信噪比下,基于特征值的盲检测算法表现出很好的检测性能,主要原因是样本协方差矩阵的最大最小特征值能够较好地捕捉信号的相关性和噪声的特性,MET 算法和MEGM 检测算法分别在瑞利衰落信道和Nakagami-m信道取得了较好的检测性能。此外,MET 算法和MEGM 算法还克服了实际系统中的噪声不确定问题。本文综合考虑MET算法和MEGM 检测算法的特点,基于不同参数α并利用样本协方差矩阵的最大特征值、迹和几何平均值得到了一种新的全盲融合检测算法(α-MTG,α-maximum eigenvalue-trace-geometric mean)。所提算法将已有的MET 算法和MEGM 检测算法作为特例。利用随机矩阵理论,分析并得到了所提算法的检测概率、虚警概率和门限的解析表达式。通过分析表明,所提算法具有恒虚警特性,克服了噪声不确定问题。仿真实验表明,所提算法的性能有较大的提高。
2 系统模型
如图1所示,本文考虑的是多天线认知无线电网络,假设有P个主用户,T个认知用户,每个认知用户配有M个接收天线用于感知主用户是否存在,认知用户的第m个天线的接收信号记为rm(n)。
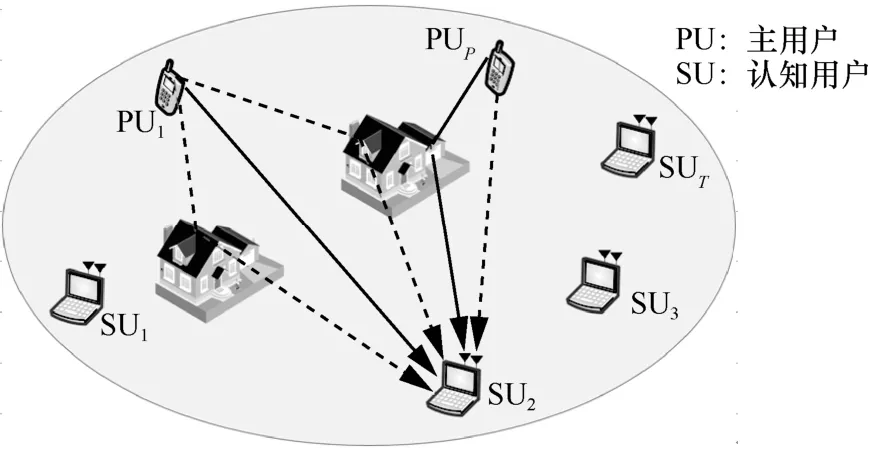
图1 多天线认知无线电系统中的频谱感知场景
频谱感知问题实际是对某一授权频段是否可用的判断,假设认知用户具有M个接收天线,不失一般性,对于主用户的感知问题可以转化为如下的二元假设检验问题。
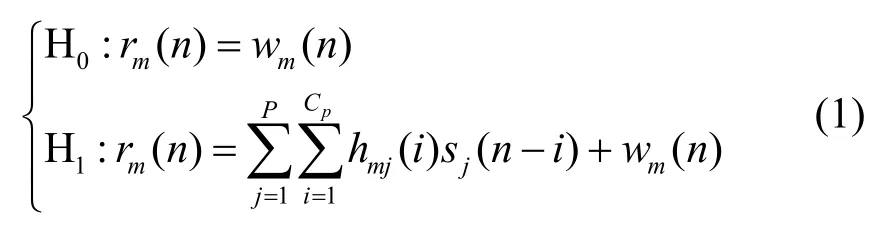
其中,m=1,…,M,n=1,…,N;H0表示主用户信号不存在,H1表示主用户信号存在;表示服从均值为0、方差为的加性高斯白噪声;sj表示第j个与噪声独立的主用户信号;hmj表示第j个主用户与认知用户第m个接收天线之间的信道响应;Cp表示信道阶数。
同一采样时刻的数据可以表示为
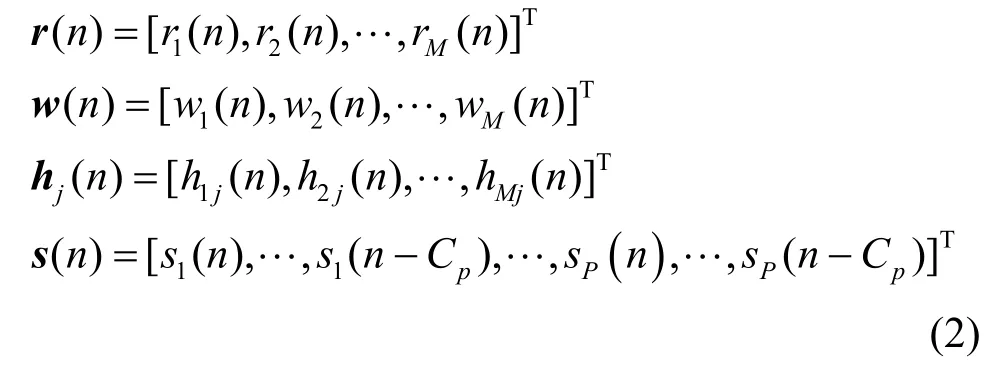
接收向量可以表示为
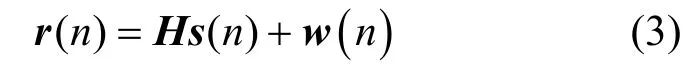
其中,H=[H1,…,HP]为主用户与认知用户之间的信道响应矩阵,且Hj=[hj(0),…,hj(Cp)]∈CM×(Cp+1)为M×(CP+1)的复矩阵。
考虑N个采样序列,接收信号的样本协方差矩阵可以表示为

3 基于特征值的融合检测算法
本节首先回顾几种经典的频谱感知算法,然后综合几种算法的优点,提出融合的特征值检测算法。
3.1 经典的频谱感知算法
盲频谱感知算法因既不需要信号功率信息也不需要噪声功率信息而被称为全盲的检测算法。典型的盲频谱感知算法包括MET 算法、MEGM 算法等。
1)MET 算法
根据奈曼-皮尔逊准则,似然比检测算法在信号和噪声信息已知时是最优的检测算法。一般信号和噪声的相关信息是未知的,此时广义似然比检测(GLRT,general likelihood ratio test)算法是解决这类问题的常用算法。GLRT 算法的主要思想是,首先对未知参数进行最大似然估计,然后利用似然比检测算法进行检测。文献[17]利用这一思想对H0和H1下的噪声功率及信道进行估计,得到了如下的GLRT 算法,其检测统计量可表示为
其中,λmax(Rr(N))、tr(Rr(N))分别表示样本协方差矩阵的最大特征值与迹。为了方便,将此算法简记为MET 算法。仿真实验表明,MET 算法在瑞利衰落信道下具有比MME 算法等更好的检测性能。
2)MEGM 算法
对于实际场景,信道状态可能不满足瑞利衰落信道,因此,为了改善在其他信道状态下认知用户对主用户的感知能力,一些检测算法被相继提出。例如,对于Nakagami-m衰落信道,文献[18]提出了MEGM 算法。MEGM 算法的检测统计量可表示为

3.2 融合的特征值检测算法
MET 算法和MEGM 算法分别在瑞利衰落信道和Nakagami-m衰落信道具有较好的检测性能。因此,本文结合这2种算法的优点,得到更加一般化的具有更高检测概率的盲频谱感知算法。所提算法的检测统计量可表示为

其中,α是正数,且α∈[0,1]。从式(7)可知,所提算法利用了样本协方差矩阵的最大特征值、迹和所有特征值的几何平均。因此,为了简便,将所提算法简记为α-MTG 。所提算法的检测统计量可以进一步表示为
根据式(8)可知,所提算法是一些现有的特征值检测算法的一般化,当α=0.5和α=1时,所提算法分别等价于MEGM 算法和MET 算法。
α-MTG 算法的详细步骤如下。
1)利用N个采样点计算接收数据的样本协方差矩阵,如式(9)所示。
2)求解样本协方差矩阵Rr(N)的特征值λi(Rr(N)),并找出最大特征值λmax(Rr(N))。
3)计算所有特征值的几何均值及样本协方差矩阵的迹。

4)计算检测统计量并与门限进行比较判决。如果统计量大于门限,则判断为主用户存在并记为H1;否则,判断为主用户不存在并记为H0。
与已有的特征值检测算法类似,所提算法也属于盲检测算法,只利用接收数据而不需要信道及信号的任何先验信息。
4 性能分析
检测概率与虚警概率是评价检测算法性能的2个重要指标,本文利用随机矩阵理论分析并推导了所提算法的检测概率和虚警概率,并根据虚警概率与门限的关系给出理论门限的解析表示。
4.1 虚警概率与门限
当没有信号时,接收信号的样本协方差矩阵表示为
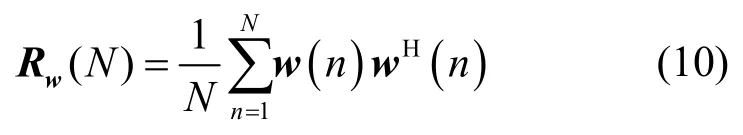
根据随机矩阵理论,矩阵Rw(N)是Wishart 矩阵。为了方便,令且假设,其最大特征值近似服从一阶Tracy-Widom 分布[20],其中
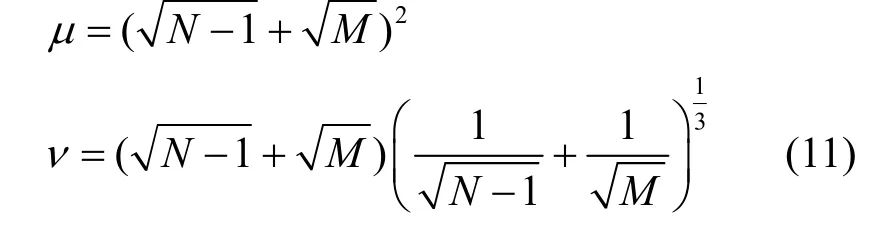
不失一般性,虚警概率表示为

其中,γ为门限。则在H0下,有

此时,虚警概率表示为

当采样点N充分大时,服从一阶Tracy-Widom 分布,因此
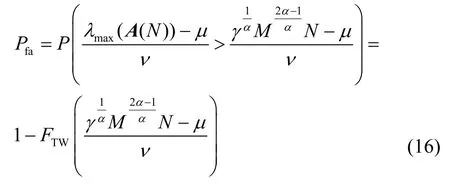
其中,μ,ν如式(11)所示。
根据虚警概率的表达式可知,虚警概率只与门限γ、采样点个数、接收天线个数及参数α有关,与噪声功率无关。因此,所提算法也属于盲频谱感知算法。
利用门限与虚警概率的关系,门限可以表示为


表1展示了MET 算法与MEGM 算法的虚警概率与门限的解析表示[18]。通过对比可知,所提算法的虚警概率及门限在α=0.5和α=1时与MEGM 算法和MET 算法等价。
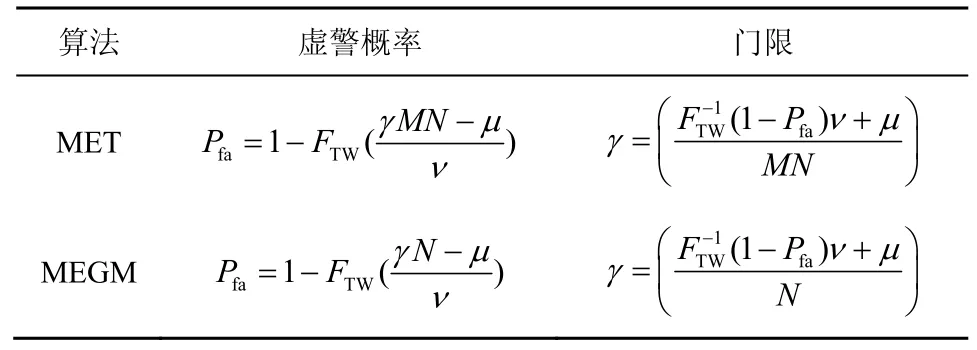
表1 MET 算法与MEGM 算法的虚警概率与门限
4.2 检测概率
在H1下,接收信号的样本协方差矩阵近似表示为
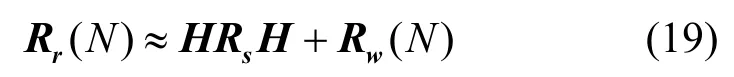
其特征值满足
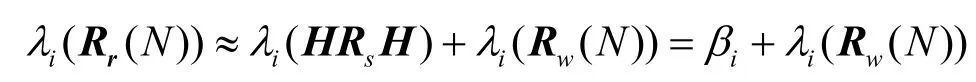
其中,βi为矩阵的特征值,且β1≥β2≥…≥βM。
检测概率进一步表示为
由噪声样本协方差矩阵的最大特征值近似服从Tracy-Widom 分布,可得

4.3 参数α的选择
由式(7)及式(17)可知,所提α-MTG 算法的检测统计量和门限除了依赖于采样点数N和接收天线数M,与参数α也是紧密相关的,参数α的选择对算法性能具有较大的影响。对给定的门限,检测统计量越大越有利于检测。考虑到判决门限也依赖于参数α,本文分析了检测统计量与门限之比随参数α的变化关系,进而得出α的选择依据。根据式(7)及式(17)可得,检测统计量与门限之比具有式(22)所示的关系。
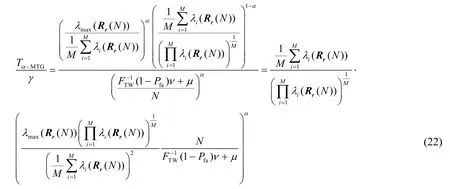
为了方便,令
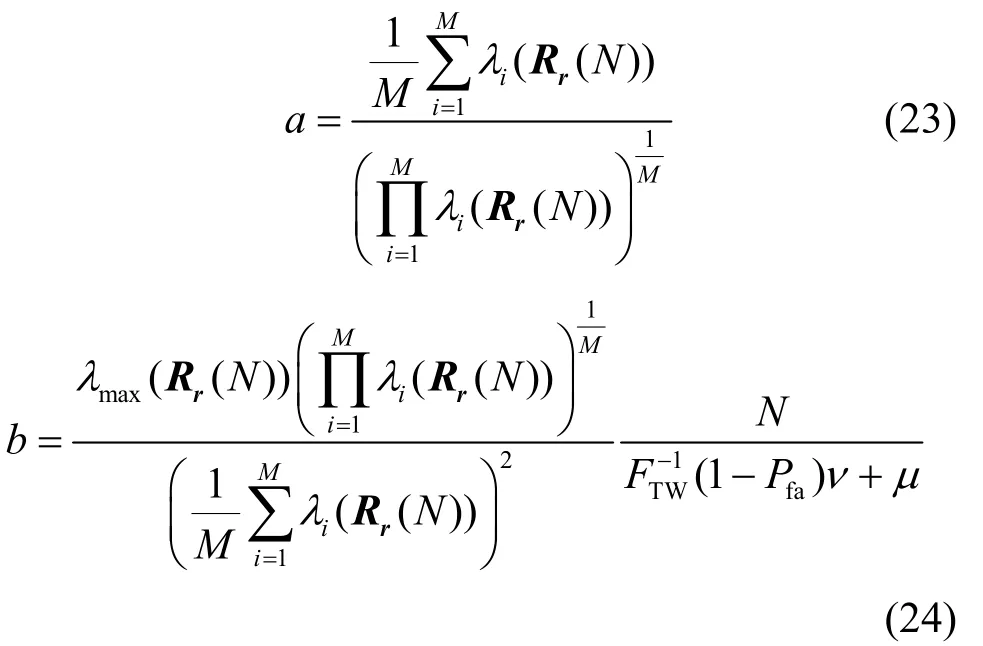
则式(22)可以表示为
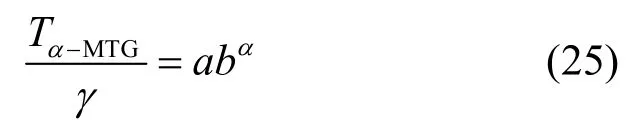
本文主要分析一个主用户存在的情况,矩阵HRs H为秩1矩阵,当N充分大时,接收信号矩阵,则
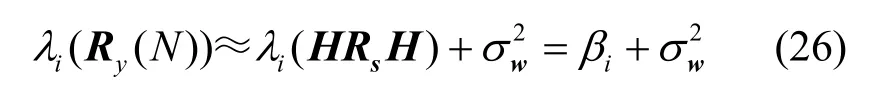
由于HRs H为秩1矩阵,因此,HRs H只有一个非0特征值,即为β1。故
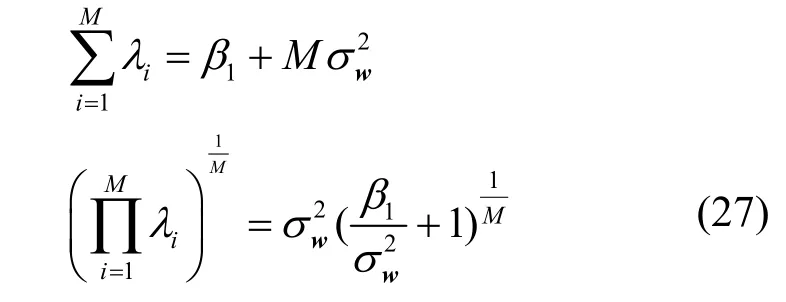
根据信噪比的定义可得
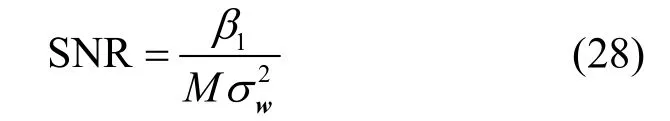
将式(28)代入式(24)可得
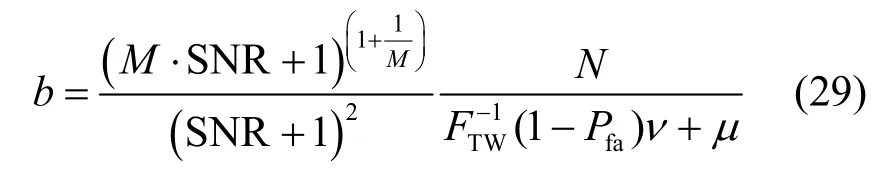
在给定N、M和虚警概率Pfa的条件下,通过对式(29)的计算可得b<1,因此,是关于α的单调递减函数。根据以上分析可知,在给定的虚警概率下,α越小,检测统计量与门限的差异性越大,越容易检测。由所提算法的检测统计量计算式即式(7)可知,当α=0.5时,所提α-MTG 算法与MEGM 算法等价;当α=1时,所提α-MTG 算法与MET 算法等价。利用以上分析可以得出,当α<0.5时,α-MTG 均能获得优于MET 算法和MEGM 算法的性能。
5 仿真实验
本节通过一些仿真实验说明所提α-MTG 算法的有效性。在每一次实验中,假设只有一个主用户独立发送BPSK(binary phase shift keying)信号,认知用户有4根接收天线,采样点数为1000。此外,本文考虑的是瑞利衰落信道,信道阶数为10。虚警概率为0.1,在每一个信噪比下,通过10000次蒙特卡罗仿真实验实现。
首先,本文基于以上仿真参数分析了不同的参数α对应的检测性能。如图2所示,在α∈[0.1,1]时,α取值越小对应的检测性能越好。当α=0.5和α=1时,所提算法的性能与已有的MEGM 算法和MET 算法性能一致。且α≤0.4时,所提算法的性能优于MEGM 算法和MET 算法。

图2 不同α对应的检测性能比较
其次,本文对比了在不同主用户数P下,所提α-MTG 算法与MET 算法、MEGM 算法、MME算法及MSEE 算法的检测性能。图3和图4分别表示P=2和P=4时,几种算法的检测概率随信噪比变化曲线。从图3和图4可知,当主用户数P增加时,所有算法的性能下降,但在不同主用户数P下,α-MTG 算法在α≤0.4时仍具有更好的检测性能。
图5和图6分别表示P=1和P=2时,不同采样点数对检测性能的影响,其中,采样点数分别设置为1000、5000和10000。为了方便,对于所提α-MTG 算法只考虑了α=0.1,0.2,0.3,0.4这4种情况。图5和图6表明,随着采样点的增加,所有算法的性能提高,其主要原因是采样点增加时样本协方差矩阵趋于统计协方差矩阵;同时,所提α-MTG 算法的性能仍然优于MET 算法、MEGM算法及MSEE 算法。

图3 P=2时,不同算法的检测性能
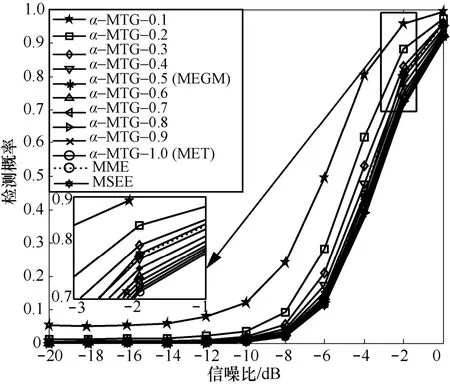
图4 P=4时,不同算法的检测性能
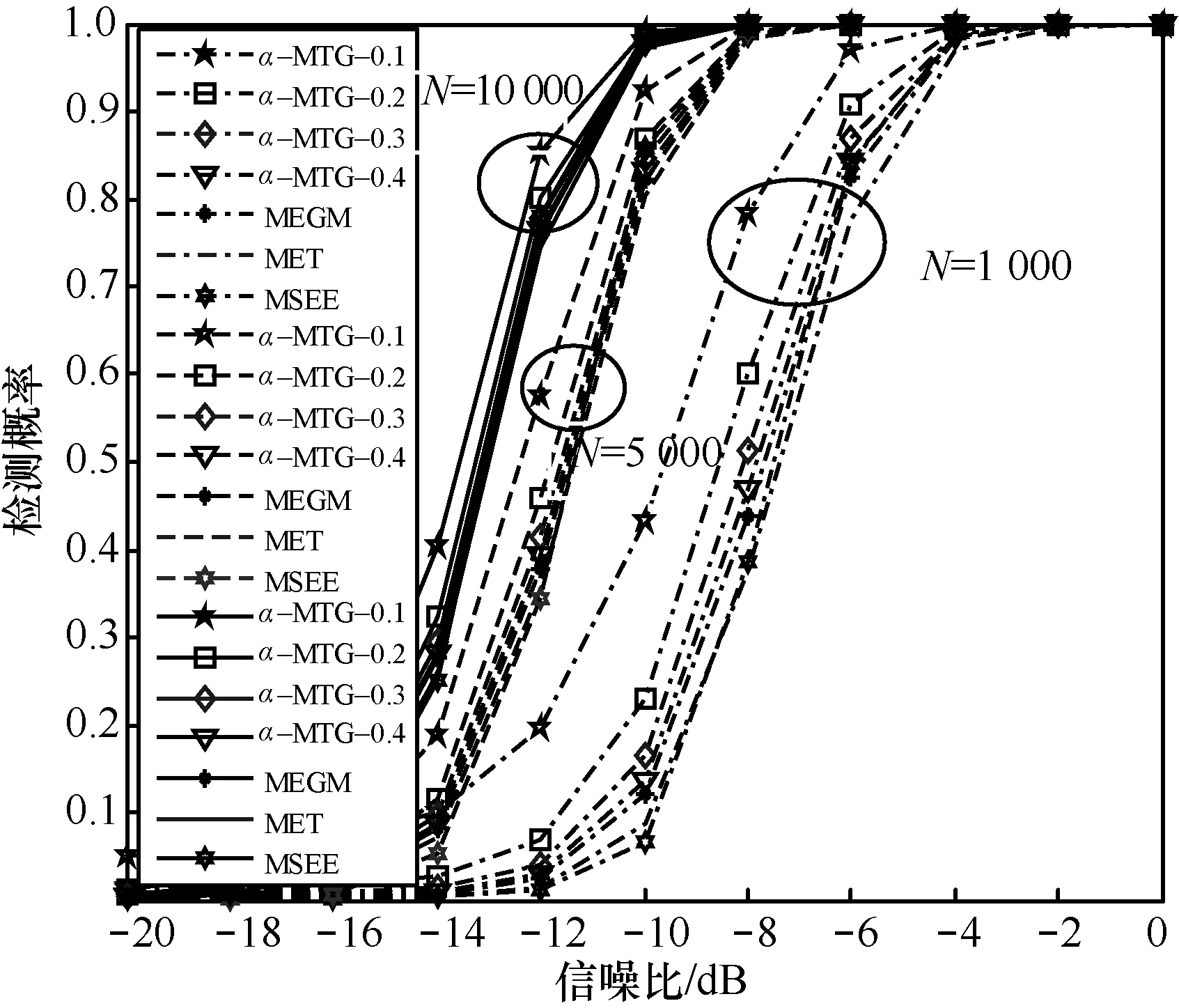
图5 P=1时,不同采样点数下,不同算法的检测性能
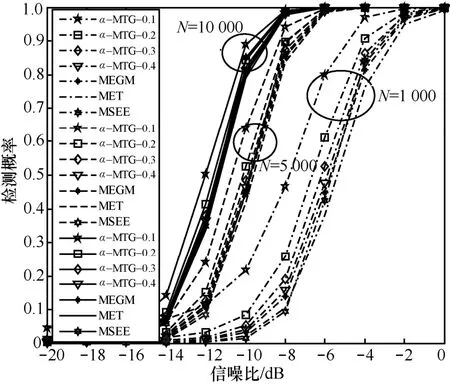
图6 P=2时,不同采样点数下,不同算法的检测性能
上述实验表明,所提α-MTG 算法不仅具有比已有的MET 算法、MEGM 算法及MSEE 算法更好的检测性能,而且具有更强的稳健性。同时,在不同用户数、不同采样点数的情况下,所提的α-MTG 算法在α=0.1时具有更高的检测性能。
6 结束语
为了更好地实现频谱复用,本文提出了一种新的基于特征值的频谱感知算法。所提的α-MTG 算法是已有的MET 算法和MEGM 算法的一般化融合形式,保持了MET 算法和MEGM算法的优点。仿真实验表明,α-MTG 算法具有比MET 算法、MEGM 算法及MSEE 算法更好的检测性能。基于本文的融合思想可以考虑很多其他的融合算法,对频谱感知算法的研究有积极的促进意义。
