GNSS水准自适应联合平差

丁阿鹿，田 婕，聂建亮，刘晓云，郭鑫伟，赵大江，张海平

(1. 北京市勘察设计研究院有限公司，北京 100038； 2. 自然资源部大地测量数据处理中心，陕西 西安 710054； 3. 山东省国土测绘院，山东 济南 250102)

GNSS与水准等大地测量观测技术是国内外学者研究地壳垂直运动的重要技术手段[1-6]。精密水准测量是地壳垂直运动监测的经典方法，是定量获得垂直形变信息精确的技术方法，20世纪初该技术就应用于东京及周边区域监测，但其观测成本高、观测周期长、观测条件要求高等因素决定了大区域精密水准测量的复测频率不高。GNSS可以进行实时观测，获取区域垂直形变信息，GNSS连续运行基准站系统可以提供连续形变信息，提高垂直形变分析控制点密度，目前该技术已成为垂直形变监测工作重要的观测技术。然而上述两种技术获得的垂直运动之间存在一个垂线偏差，文献[1]分析了小范围内监测点的大地高变化速度近似替代正常高变化速度；两类观测数据所采用不同的观测手段、噪声模型、起算基准、数据处理方法，导致两类垂直运动之间可能存在一定的系统偏差。为了充分发挥GNSS和水准对垂直运动的贡献，需要根据GNSS、水准精度实现多源数据融合。文献[6]提出了大地测量数据融合的基于观测信息和基于平差结果的融合模式，证明两种模式理论上是等价的。考虑到从原始观测值层面融合难度较大，可以采用水准高差观测值和GNSS垂直运动速度结果进行融合。这样如何有效确定水准高差观测值权矩阵与GNSS垂直运动速度权矩阵之间的比例关系成为实现数据融合的关键。目前，国内外学者常用两种方法确定权比：①方差分量估计方法，该方法能够有效协调不同观测之间的权重，已应用于地震反演[8]、地球重力场[9]、GPS网平差[10]、自适应滤波[11]、地面沉降[12]等方面；②利用反演结果分辨率与反演残差的折中曲线确定权比值的方法，已应用于地震反演[13]、地壳垂直运动[14]。而方差分量估计方法是国内外学者青睐的权比确定方法。在以上研究的基础上，将水准原始高差观测值和GNSS垂直运动速度结果作为数据融合观测值，将一定数量GNSS水准点的垂直运动速度作为限制条件，利用方差分量估计方法自适应调整GNSS、水准观测值权比，采用相关抗差估计方法抑制异常误差影响，从而实现GNSS与水准的垂直运动融合，以提高区域垂直运动模型的精度。

1 GNSS水准联合平差

水准观测可以获取高精度正常高方向形变信息，GNSS观测能够获得大地高方向变化量，两类形变信息之间存在较小差异，可用大地高变化代替正常高变化[1]。文献[1，8]联合GNSS连续站的高程分量变化速率与复测水准资料进行动态平差，解决了水准高程变化基准问题。

GNSS与水准联合平差的误差方程由水准高差观测值误差方程与GNSS高程方向速度值误差方程组成。选取一定数量的GNSS水准点作为约束点，则联合平差误差方程为

(1)

联合平差观测值的权矩阵为

(2)

式中，n0为水准高差观测值个数；m为GNSS大地高速度个数；α为两类观测值间的权比；水准高差观测值权矩阵PL按照测站数定权；GNSS垂直运动速度值的权矩阵PG为垂直运动速度平差精度协因数矩阵的逆矩阵。为了控制观测数据中异常误差影响，采用相关观测抗差估计最小二乘方法[15]降低异常观测值的权值，构造双因子相关等价权矩阵[15]。

2 自适应联合平差

理论上基于观测信息、中间结果和最终平差结果的数据融合是一致的，为了得到可靠的计算结果，确定不同观测数据之间合理的权比α显得尤为重要。折中曲线确定权比方法依靠经验确定两类观测值之间的权比[12-13]，无法实现自适应纠正，而方差分量估计方法依据验后估计精度逐步调整不同观测值之间的权比，使权比更接近真实比例关系。

Helmert方差分量估计方法得到的第i0类观测值的残差平方和为

(3)

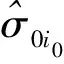
Helmert方差分量估计的Baumker简化公式为

(4)

式中，ni0为第i0类观测值的个数。不同类观测值之间的权比α为

(5)

经过多次迭代，直到α趋于稳定。

3 算例分析

算例采用2006、2015年山东省似大地水准面精化GNSS、水准观测数据。水准网观测按照二等水准网观测纲要于2004—2006、2015年进行观测，GNSS控制网按照C级网观测纲要于2004—2006、2015年同步进行数据采集(水准路线及C级点示意图如图1所示)，其中两期分别有1337、1105个水准高差观测值，两期GNSS观测共有153个C级重合点。利用两期GNSS控制网、水准网观测数据，采用联合平差方法实现GNSS水准融合，从而获得山东省区域垂直形变信息。

为了实现水准观测值与GNSS垂直运动速度联合平差，采用如下步骤处理：①使用GAMIT/GLOBK软件处理GNSS数据，获得GNSS垂直运动速度及协方差矩阵；②整理两期水准网重合点数据，水准网平差起算点采用青岛国家水准原点，其速度为+2.2 mm/a[4]；③组建联合平差观测误差方程，水准观测值根据测站数定权，GNSS根据协方差矩阵定权，两类观测值之间的权比α采用Helmert方差分量估计方法确定，从而获取垂直运动速度。

为了比较GNSS水准融合效果，采用4种方案进行比较分析：

(1) 利用最小二乘方法进行水准网整体平差。

(2) 利用抗差最小二乘进行水准网整体平差。

(3) 选取两类高程变化一致性较好的60个GNSS水准并置点作为约束点，利用联合平差方法进行融合，权比利用Helmert方差分量估计方法确定。

(4) 同方案(3)，构造双因子相关等价权函数削弱异常观测值的权值。

4种方案计算结果见表1，误差曲线如图2所示。由计算结果可以得到如下初步结论:

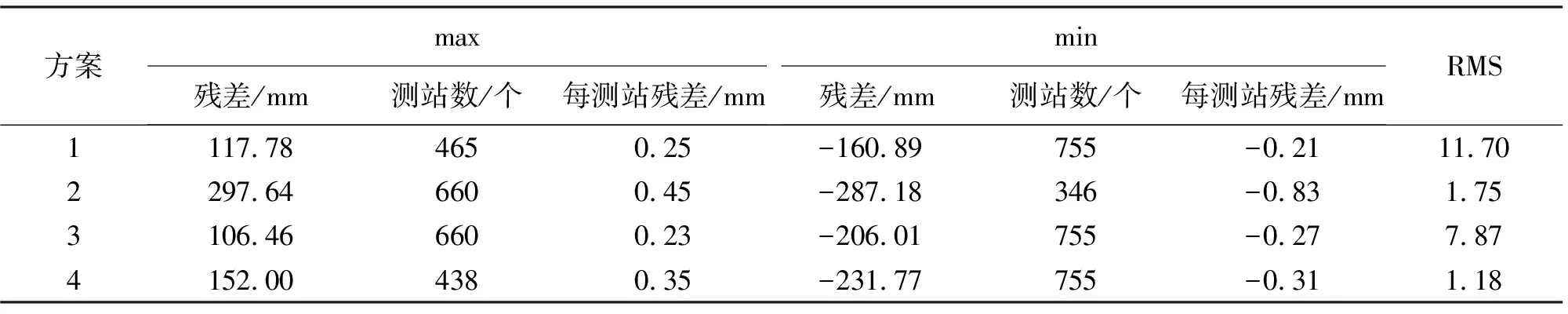
表1 各方案误差统计信息

(1) GNSS水准联合平差与水准网平差相比，联合平差精度有一定程度提高。联合平差充分利用了水准高差观测值和GNSS平差结果，通过约束GNSS水准点垂直运动速度建立水准垂直运动速度与GNSS垂直运动速度之间的关联，实现水准高差观测值与GNSS垂直运动速度的有效融合，从而提高水准环包围区域的垂直形变信息精度。

(2) 方案2、4与方案1、3相比，对应平差精度都有一定程度提高。方案2、4采用抗差估计方法降低了异常观测值的权值，削弱了异常误差影响，提高了垂直运动估计精度；方案3、4与方案1、2相比，利用Helmert方差分量估计方法根据验后残差自动调整两类观测值之间的权比，实现了GNSS与水准的有效数据融合，提高了垂直形变信息的可靠性；由于误差转移、处理策略的不同，联合平差与水准网动态平差残差最大值、最小值的位置可能会存在一定不同。

(3) 利用GNSS水准数据获取了山东省西降东升、北降南升的整体垂直运动趋势。西北、西南部地区沉降严重，整体呈下降趋势，垂直运动速度平均为20.0 mm/a；德州、菏泽、广饶地区出现3个沉降中心，主要由于地下水过度开采导致地面沉降，其中广饶地区沉降最严重，10年平均沉降速度70.0 mm/a左右；而在胶东半岛呈5.0 mm/a的上升趋势。

致谢：感谢山东国土测绘院与陆态网络中心提供的GNSS试验观测数据。