磁通反向永磁电机齿槽转矩分析与抑制
2019-12-02张颖博
张颖博,李 洋
(阜新德尔汽车部件股份有限公司,辽宁 阜新 100023)
0 引 言
随着永磁材料的不断发展,永磁无刷电机(在工业驱动、国防军工、可再生能源、家用电器等领域得到不断推广和应用。在传统转子永磁型电机中,永磁体位于电机转子侧,通常需要对转子采取特殊的加固措施以克服高速运转时的离心力,这必将增加工艺复杂性;同时由于转子散热困难,这势必会导致永磁体因高温发生不可逆退磁的风险增加。为克服上述转子永磁型电机的缺点,近二十年出现了将永磁体安置于定子侧的定子永磁型无刷电机,受到了日益广泛的关注[1-3]。
磁通反向电机作为定子永磁型电机的一种,在1997年被罗马尼亚学者I. Boldea教授首先提出[4]。其可被视为永磁电机与开关磁阻电机相结合的产物,该类型电机继承了两种电机的优点,散热性能好、功率(转矩)密度高、抗去磁能力强、转子结构简单、容错性能好等[3,5]。然而,由于特殊的双凸极结构,磁通反向电机通常具有较大的齿槽转矩,这势必会导致电机产生额外的转矩与转速脉动及振动噪声,尤其在低速工况下,这种影响更为严重。因此必须对该电机的齿槽转矩加以重视。到目前为止,已有学者对其进行了研究,并取得了一定的成果。
文献[6]基于变网络等效磁路法,建立了磁通反向电机的等效磁网络模型,计算电机的空载磁链、反电动势、电感等静态特性。文献[7-8]借助二维有限元法,以6槽/8极结构磁通反向电机为例,研究了转子齿宽、转子开辅助槽、永磁体削角、转子齿顶削角和转子斜槽对齿槽转矩的影响。文献[9]采用转子齿组合的方法以抑制磁通反向电机的齿槽转矩。文献[10-11]对传统转子结构进行优化,提出了一种转子大小齿间隔加分段结构以抑制齿槽转矩。我国磁通反向电机齿槽转矩的研究起步较晚,对于深入分析影响齿槽转矩关键参数迫在眉睫。
本文基于磁共能法及磁导-磁势模型,首先推导了磁通反向永磁电机齿槽转矩解析模型;在此模型基础之上,分析了电机参数对齿槽转矩波形及其谐波分布的影响;研究了如何优选定、转子齿宽以降低齿槽转矩的方法;最后采用有限元法,以6/8结构磁通反向电机为例,验证了分析正确性。
1 齿槽转矩解析模型的建立
本部分内容以磁通反向永磁电机为研究对象(如图1所示),基于磁共能法及磁势-磁导模型,推导了该类电机齿槽转矩的解析模型。根据文献[5],该结构电机相空载反电动势波形趋近于正弦波,适合BLAC控制。
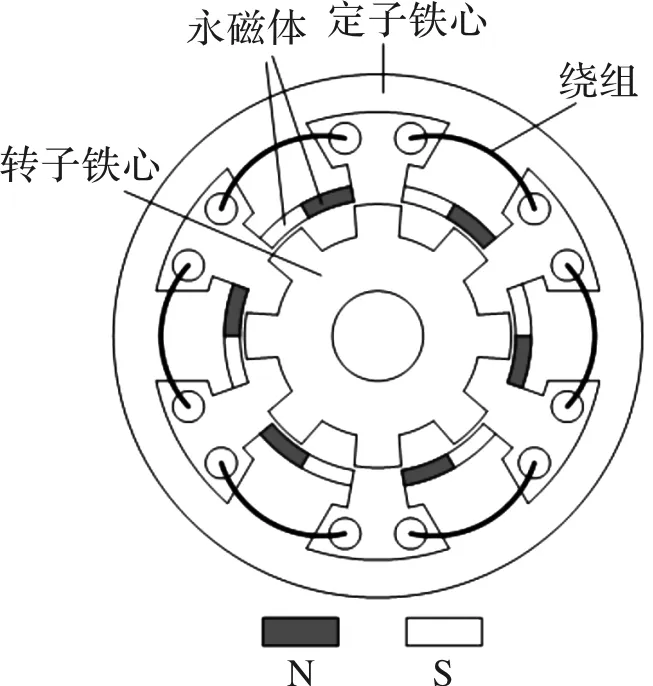
图1 磁通反向永磁电机横截面示意图
为了便于分析,首先作如下基本假设:
(1)定、转子铁心的磁导率无穷大,即不考虑磁路饱和。
(2)忽略漏磁的影响。
(3)认为气隙磁密只有径向分量。
一般而言,永磁电机的齿槽转矩可被认为是电机不通电时磁场能量W相对于位置角α的负导数,即:
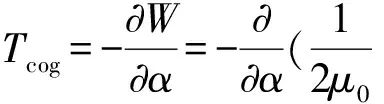
(1)
式中,μ0为真空磁导率;B(θ,α)为气隙磁密;V为气隙体积;θ为定子沿圆周方向的角度;α为转子位置角;Tcog为电机的齿槽转矩。
在理想空载情况下,永磁电机的气隙磁密可由永磁磁动势与气隙比磁导的乘积表示[12],即:
B(θ,α)=Fpm(θ)Λ(θ,α)
(2)
将式(2)代入式(1)中,可得到:
(3)
根据式(3)可知,若要得到电机的齿槽转矩,首先必须能够分别求出永磁磁动势平方与气隙比磁导平方的数学表达式。
1.1 永磁磁动势模型
在图1所示磁通反向电机某一时刻其磁动势的空间分布如图2(a)所示,而磁动势平方的空间分布如图2(b)所示,此处需要说明的是图2中θst=2θpm。
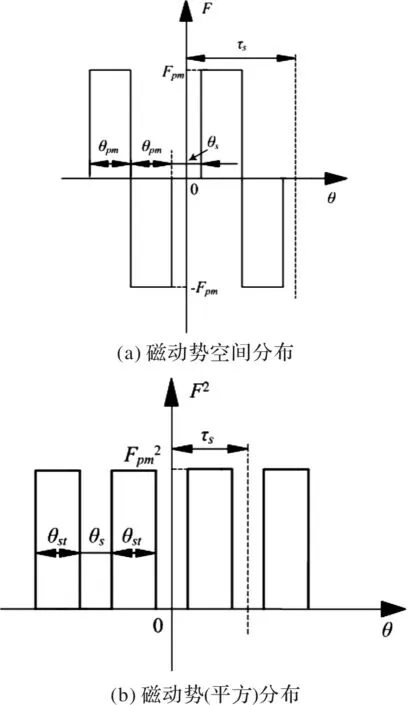
图2 永磁磁动势及磁动势平方分布
若将图2(b)中的磁动势平方分布用数学表达式表示,则可得到:
(4)
式中,Fpm为永磁磁动势幅值;Ns为定子槽数;θs、θst分别为定子槽宽和齿宽(用弧度表示);s为定子极距(用弧度表示)。
将上式展开成傅里叶极数的形式,并经过简单数学变换可得到:
(5)
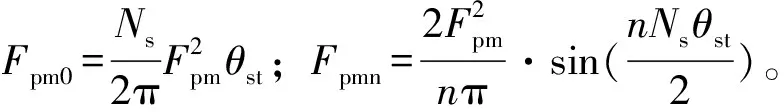
1.2 气隙比磁导模型
磁通反向电机气隙比磁导空间分布如图3所示,由其可得比磁导的数学表达式(6)。
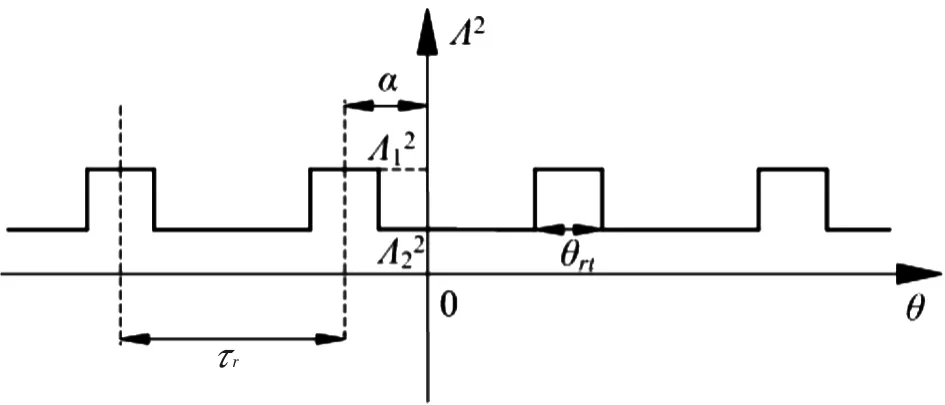
图3 气隙比磁导分布
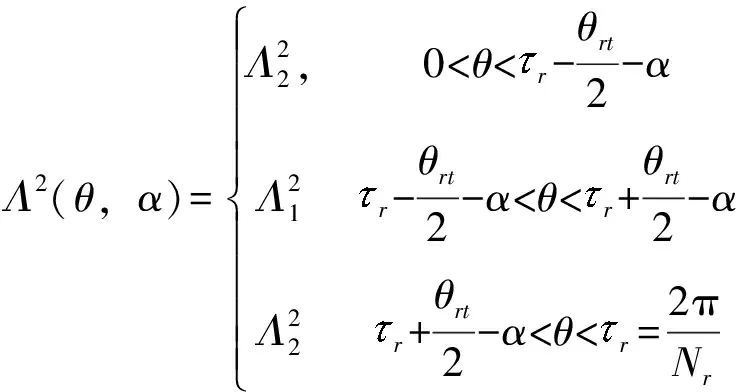
(6)
式中,Λ1、Λ2分别为转子齿和槽部分的气隙比磁导;θrt为转子齿宽(用弧度表示);r为转子极距;Nr为转子极数。
将式(6)展开成傅里叶极数,得到:
(7)
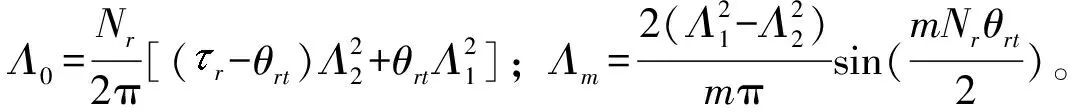
1.3 齿槽转矩表达式
将式(5)、式(7)代入式(3),可得到
(8)
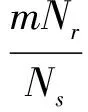
从式(8)可以看出,齿槽转矩谐波次数为mNr,即kLCM(Ns,Nr),若令LCM(Ns,Nr)次为基波,则kLCM(Ns,Nr)次为k次谐波,下文中的k次谐波皆基于这个假设。
从式(8)中还可以看出,齿槽转矩的基波周期用机械角度可表示为
(9)
式中,LCM(Ns,Nr)为Ns和Nr的最小公倍数。
2 齿槽转矩分析
为了验证以上分析,以6/8结构磁通反向电机为例进行阐明,其电机截面图已在图1中给出,相关电机参数如表1所示。
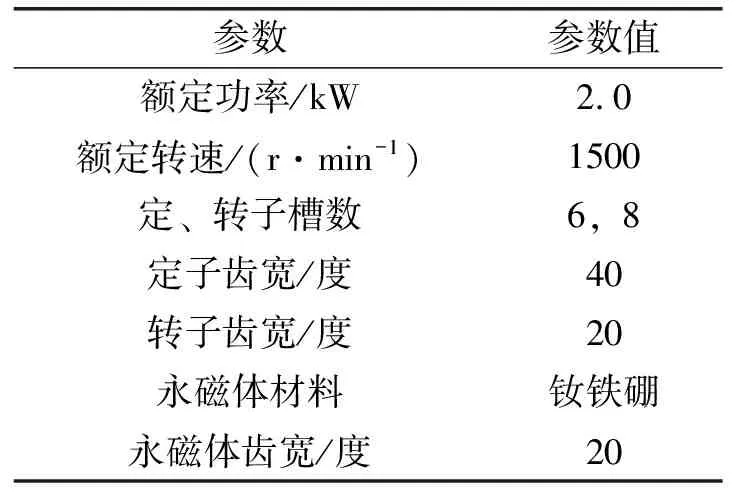
表1 电机参数
2.1 齿槽转矩波形
图4通过有限元计算得到的电机齿槽转矩波形图。对于该结构,通过式(9)可知,其齿槽转矩的机械周期为15°,与图4相符,进一步验证了理论分析的正确性。
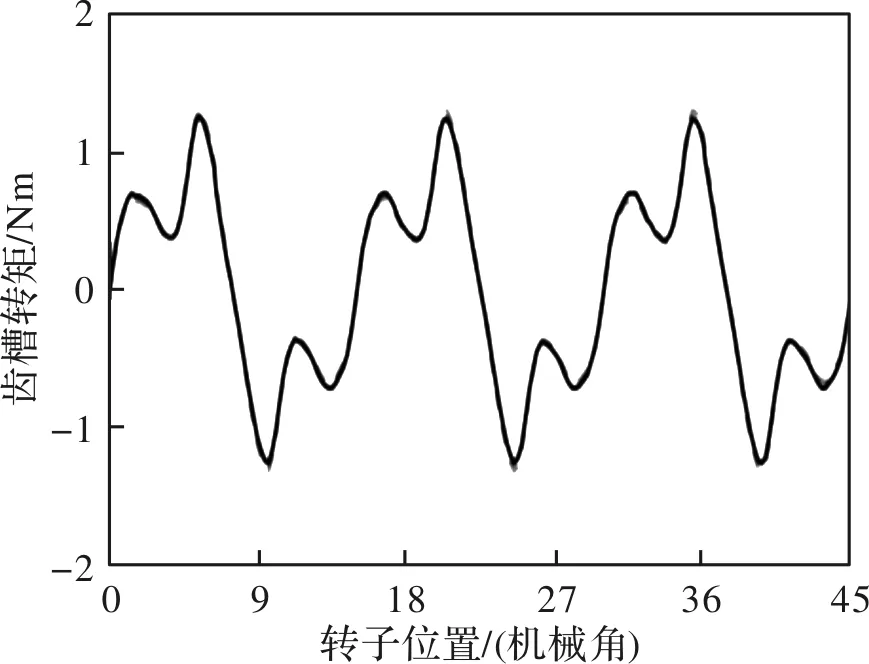
图4 磁通反向电机齿槽转矩波形
图5为齿槽转矩波形的谐波分布,可以看出除基波以外,2次、3次谐波分量也占了很大比例。
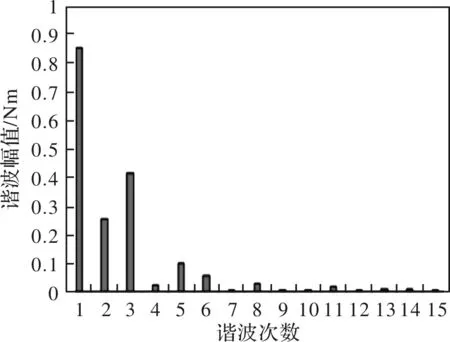
图5 齿槽转矩波形谐波分布
2.2 齿槽转矩谐波分析
将Fpmn、Λm表达式代入式(8),可进一步得到齿槽转矩与电机参数的关系式:
(10)
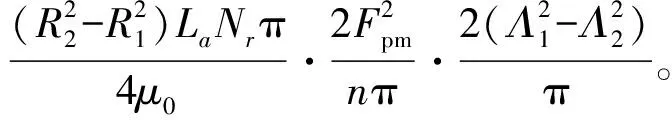
从式(10)中我们可以看到,磁通反向电机齿槽转矩主要与定子齿数Ns和齿宽θst、转子极数Nr、转子齿宽θrt等设计参数有关。
此外,从式(10)中还可以看出,若转子齿宽的取值满足以下等式时,相应的k次齿槽转矩谐波分量就会被削弱。
(11)
同理,若定子齿宽满足下式时,相应的k次齿槽转矩谐波分量也会被削弱。
(12)
以6/8结构磁通反向电机为例,由上述两个公式可知:若要削弱齿槽转矩的基波,则θrt和θst可分别取15k1和15k2(单位:度),即15°、30°、45°等;同理,若要削弱二次谐波,则θrt和θst可分别取7.5k1和7.5k2(单位:度),即7.5°、15°、22.5°等;消除其它更高次谐波也可按照此分析方法。可求得各次谐波幅值取最小值时相应的电机参数具体数值,取前5次谐波列于表2中。
图6与图7为通过有限元仿真得到的齿槽转矩各谐波幅值与定、转子齿宽取值的变化关系图。需要指出的是,研究图6的变化规律时保持转子齿宽为初始设计值20°不变;而研究图7的变化规律时则保持定子齿宽为初始设计值40°不变,在定转子齿宽取值范围内,仿真得到齿槽转矩的最小值。 从图中可以看到,随着定/转子齿宽的变化,齿槽转矩各次谐波幅值也随之不断变化。对于初始设计,即θrt=20°、θst=40°,由前面图5分析可知,齿槽转矩基波占所有谐波的比例最大,其次是3次谐波,再是2次谐波、5次谐波、4次谐波。而随着定/转子齿宽不断变化的过程中,虽然在大部分情况下,齿槽转矩基波幅值占主导地位,但是也有特殊情况。例如当定子齿宽取43°~45°或转子齿宽取14°~17°时,二次谐波居于主导地位。

表2 不同定、转子齿宽时的谐波分量
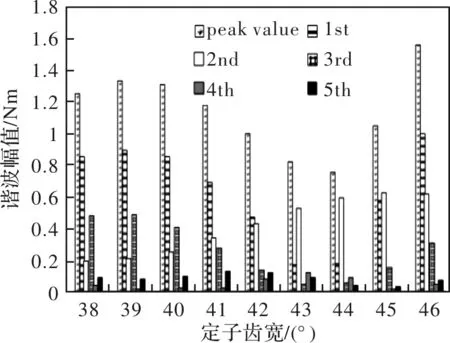
图6 齿槽转矩谐波随定子齿宽变化
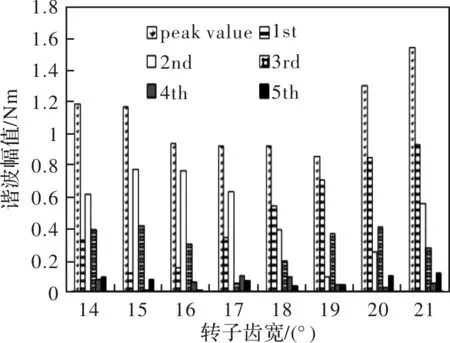
图7 齿槽转矩谐波随转子齿宽变化
此外,可以得到当定/转子齿宽取43°/15°时,基波幅值达到最小;当定/转子齿宽取38°/19°时,二次谐波幅值达到最小;当定/转子齿宽取43°/17°时,三次谐波幅值达到最小;当定/转子齿宽取39°、45°/15°、20°时,四次谐波幅值达到最小;当定/转子齿宽取39°、44°/16°、18°时,五次谐波幅值达到最小。与表2中理论值相比,整体上较为吻合,但也存在少许偏差,这是因为理论公式推导时忽略了漏磁和饱和因素的影响。
由以上分析可以看出,根据不同定、转子齿宽组合对齿槽转矩及其谐波分布的影响规律,因此,合理选取定、转子齿宽组合可以降低电机齿槽转矩。在电机设计初始阶段,可以采用这个方法抑制齿槽转矩对电机性能的影响。
3 从设计角度优化齿槽转矩
对于一台特定的电机,若要降低其齿槽转矩,最简单直接的方法就是从电机尺寸参数上着手,通过优选该数值,以达到抑制齿槽转矩的目的。本部分从电机定、转子齿宽出发,通过选取合理的齿宽组合以降低齿槽转矩。
从2.1节分析可知,对于该结构电机,1-3次齿槽转矩谐波分量较大;另一方面又由图6分析可以发现,当定子齿宽取43°时可以显著削弱齿槽转矩基波和三次谐波幅值,但二次谐波幅值仍然较大;而通过图7分析可知,当转子齿宽取19°时可以大大削弱齿槽转矩二次谐波。因此,可以推断出当定、转子齿宽分别取43°和19°时(优化模型),可以大大减小电机齿槽转矩。图8为通过有限元计算,对比齿宽改变前后的齿槽转矩变化。从图8(a)中可以发现,齿槽转矩幅值确实被大大削弱;而从图8(b)中可以发现,采用上述齿宽后,齿槽转矩1至3次谐波都被大幅度削弱,与上述预期相一致。然而,采用这组齿宽后,会导致四次谐波的增加,因此,若要进一步降低该电机的齿槽转矩,需要着重削弱该次谐波(本文不做进一步的优化)。
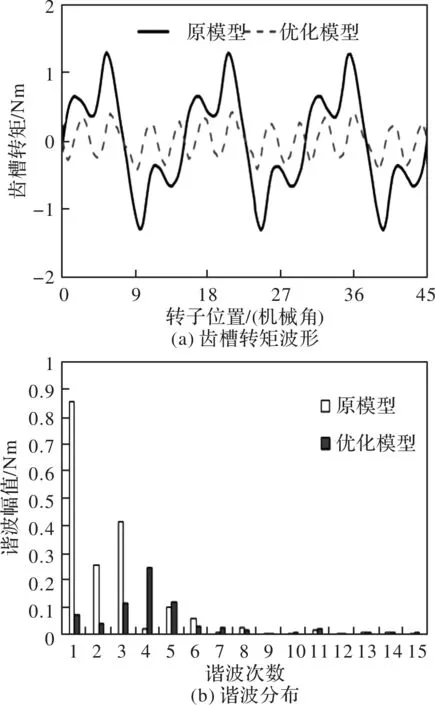
图8 6/8结构磁通反向电机的齿槽转矩对比
图9对比了齿宽优化前后的空载相反电动势波形(1500 r/min),可见优化后的模型反电动势幅值有所增加,这将有利于提高电机出力。此外,图10对比了齿宽优化前后电机的额定转矩(相电流峰值为5.54 A)。通过数据分析可以得到:优化后电机转矩脉动从原来的39.0%降低到16.0%,平均转矩从原来的6.5 Nm增加到6.9 Nm。
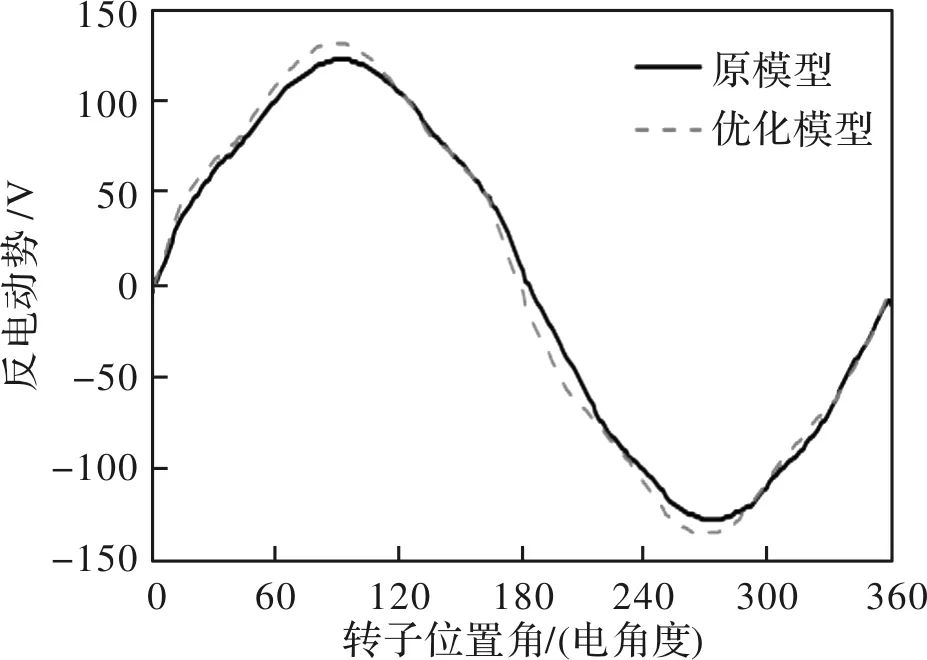
图9 优化前后空载感应电势对比
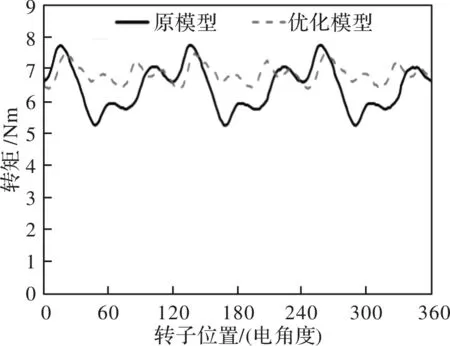
图10 优化前后额定转矩对比
4 结 论
本文基于磁共能法及磁势-磁导模型,推导了磁通反向永磁电机的齿槽转矩解析模型。在此模型基础之上,进而研究了电机参数(包括定子齿宽和转子齿宽)对齿槽转矩波形及其谐波分布的影响规律;提出了如何优选定、转子齿宽以降低齿槽转矩的方法;最后,借助有限元法,以6/8结构磁通反向电机为例,验证了分析的正确性。得到如下结论:
(1)定、转子齿宽参数对磁通反向电机齿槽转矩的影响较大;随着定、转子齿宽的变化,齿槽转矩各谐波分量占比也不断变化,基波分量并不是一直占主导地位。
(2)合理地选取定、转子齿宽组合,可以削弱特定的齿槽转矩谐波分量,进而达到抑制齿槽转矩的目的。因此,可以采用此方法,在电机设计初始阶段抑制齿槽转矩。
