基于改进PDF的粒子数量在线可调粒子滤波算法
2019-11-30袁帅苏航
袁帅 苏航


摘 要:粒子滤波运行效率的一个关键参数是粒子数量。算法运行使用的粒子数量越多,滤波器得到的分布越接近真实分布,然而计算成本会随着粒子数量增加而剧增。所以需要合理选择一定数量的粒子提高滤波运行效率。该文提出在线方法调整粒子数量,实时评估收敛性,调整算法中使用的粒子数量M。参考辅助粒子滤波的思想,将即时的观测值信息引入到重要性概率密度函数当中,改进粒子分布概率密度。实验结果对整个算法的改进进行仿真验证,证明了改进算法的可行性。
关键词:粒子滤波方法 在线调整粒子数量 辅助状态变量
中图分类号:TP391 文献标识码:A 文章编号:1672-3791(2019)09(c)-0199-03
1 粒子滤波方法介绍
粒子滤波的作用主要是用于参数估计,基于蒙特卡洛仿真的近似贝叶斯滤波算法,通过几轮蒙特卡洛试验,得到优化参数。其核心思想是用一些离散随机采样点来近似随机变量的概率密度函数,以样本均值代替积分运算,从而获得状态的最小方差估计。
2 粒子在线调整方法研究
在每次迭代中,从预测概率分布函数中生成K“虚拟观察值”来近似预测,分别表示为。通过收集一系列例如的统计数据,很容易测试它们的经验分布是否接近均匀。如果是任意独立且都来自同一个连续的概率分布,那么随机变量AK,t的概率质量函数是,其中是一个均匀分布,进行皮尔森卡方统计测试。根据方程式计算,得到P*K,t值。P*K,t值用于检验St的经验分布是否均匀。大的P*K,t值表示样本的匹配良好。而小的P*K,t值的样本表示不匹配。
将P*K,t值与两个不同的阈值进行比较:低阈值Pl和高阈值Ph。如果P*K,t≤Pl,则根据规则Mt=fup(Mt-1)增加粒子数;而如果P*K,t≥Ph,则根据规则Mt=fdown(Mt-1)减少粒子数。当Pl﹤P*K,t﹤Ph时,颗粒的数量保持固定。我们通过调整低阈值Pl和高阈值Ph这两个参数对滤波器性能与计算成本折中。
3 基于辅助状态变量的改进粒子分布概率密度方法研究
辅助粒子滤波方法是在考虑上一时刻的经验分布同时,也考虑当前观测值的影响。该文参考辅助粒子滤波的思想,将即时的观测值信息引入到重要性概率密度函数当中,这样不但可以提高滤波效率,也充分运用了当前的观测量,使得粒子分布更接近真实分布。
基于辅助状态变量的粒子滤波重要性概率密度函数为:
其中,辅助状态变量uki是在给定下的某些特征,通常是的期望均值,基于辅助状态变量的粒子滤波算法一般策略如下:
(6)计算有效粒子数Neff,如果Neff﹤Nth,Nth为系统阈值,续进行重采样,重采样后新的粒子权值赋值为。
Neff用来计算算法的退化情况。Neff越小,退化越严重。为系统设置一个阈值Nth,这样能有效控制系统的退化。
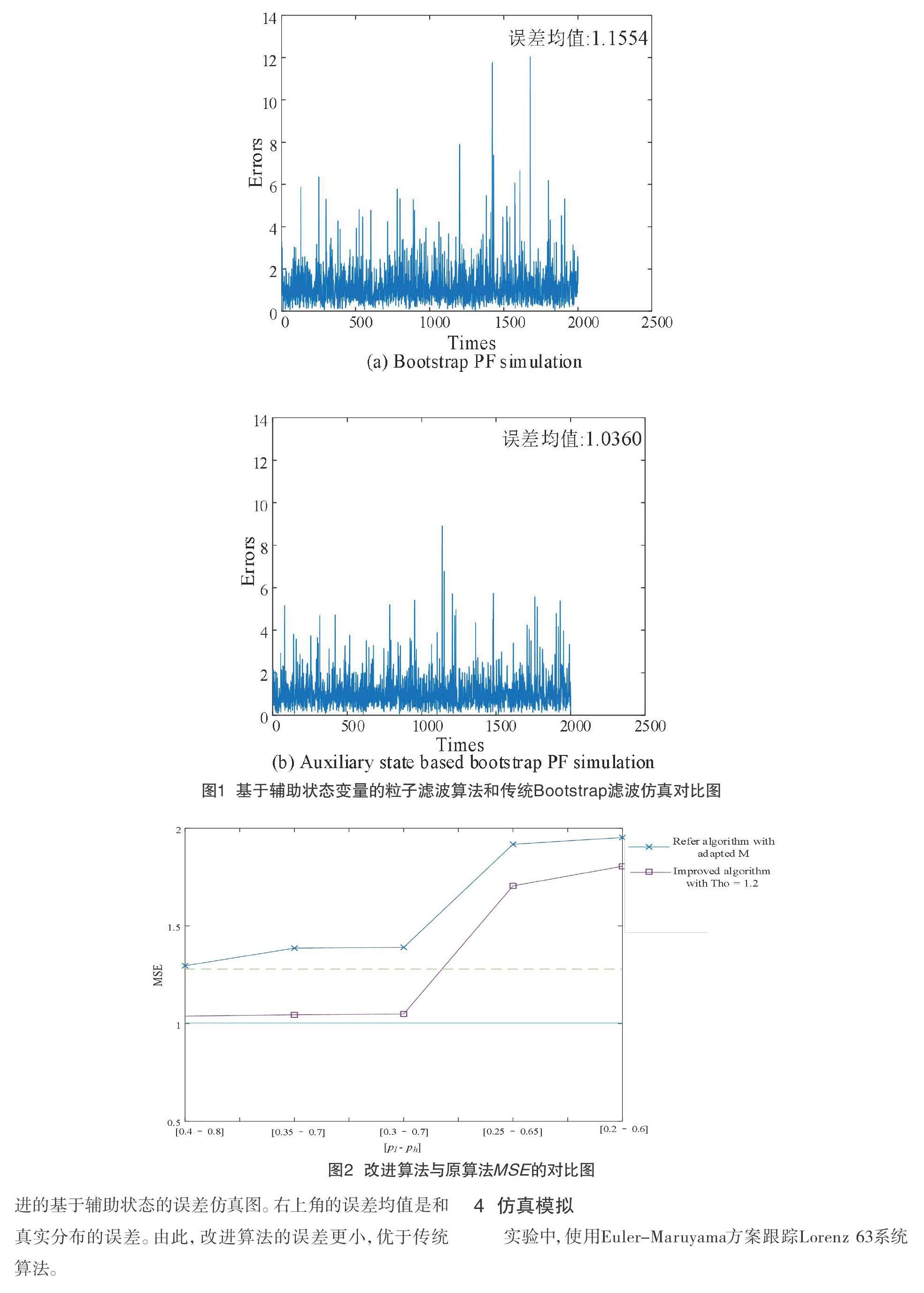
对上述方法进行了仿真验证,改进的基于辅助状态变量的粒子滤波算法和传统的Bootstrap算法进行了对比,如图1所示。
图1(a)是传统粒子滤波算法的误差仿真图,图1(b)是改进的基于辅助状态的误差仿真图。右上角的误差均值是和真实分布的误差。由此,改进算法的误差更小,优于传统算法。
4 仿真模拟
实验中,使用Euler-Maruyama方案跟踪Lorenz 63系统三维随机过程{X(s)}s∈(0,∞)。实验中使用离散时间版本,积分步长为△=10-3。每200个离散时间步骤观察系统。具体由Yt=X1,200t+Vt收集观察值。其中观测噪声{Vt}t=1,2,…是一系列独立且相同分布的正态随机变量,零均值和方差σ2=。
跟踪系统的后验概率测量序列可生成一系列T=2000的合成观测值,{yt;t=1,…,2000},对应Euler-Maruyama方案中的4×105个离散时间步长(每200个步骤观察一次)。对于基础离散时间系统,离散时间近似的时间尺度是n=200t,所以每200步进行重采样步骤。
实验开始时,运行具有足够多数量的粒子M=5000。然后运行提出的算法,减少粒子数量让M达到滤波器性能和计算成本的折中。这一点由P值的操作范围控制,P值又由一对阈值限定。实验结果如图2所示。
5 结语
粒子滤波运行效率的一个关键参数是粒子数量。该文利用皮尔森卡方评估收敛性的方法在线调整粒子数量。粒子滤波重采样方法解决粒子退化问题,但也会引起粒子多样性减弱的问题。该文从粒子滤波重要性概率密度方面考虑,提高粒子滤波中粒子分布概率密度的准确性,提出基于辅助状態变量的改进粒子分布概率密度方法。通过仿真验证了算法的有效性。
参考文献
[1] Elvira Víctor, Míguez Joaquín,Djuri? Petar M.Adapting the Number of Particles in Sequential Monte Carlo Methods through an Online Scheme for Convergence Assessment[A].IEEE Transactions on Signal Processing[C].2015.
[2] 胡士强.粒子滤波原理及其应用[M].北京:科学出版社,2010.
[3] 苟清松.多目标粒子滤波检测前跟踪算法研究[D].电子科技大学,2015.
