保持算子†-乘积幂等性的映射
2019-11-29董改芳
董改芳
朔州师范高等专科学校, 山西 朔州 036002
关于算子代数上保持问题的研究已经得到了许多有意义的成果[1~7].设H是复的无限维的完备的不定内积空间,B(H)是由H上所有有界线性算子构成的代数,Ω⊂B(H),I∈Ω,C*I1(H)⊂Ω,且∀A∈Ω,Gcv{A,I}⊆Ω,Φ是Ω上保持算子†-乘积幂等性的映射,Φ(I)=I.文献[6]给出了Φ的具体形式.本文证明了此结论对于dimH≥3也成立,并给出Mn(C)上Φ的具体形式.
1 符号及概念
I是单位元,C*,R*是非零复数集和实数集,I*(H),I1(H)是B(H)的非零幂等元和一秩幂等元集合.dimH表示H的维数.rank(P),rng(P),ker(P)是P的秩、值域和零空间.B(H)同构于n级矩阵代数Mn(C).I*(H),I1(H)分别记I*(n),I1(n).称Φ为Ω上保持算子†-乘积幂等性的映射,若∀A,B∈Ω,AB+∈I*(H)⟺Φ(A)Φ(B)+∈I*(H).Gcv{A,I}={λA+(1-λ)I,λ∈C}为A,I的广义凸组合.
2 主要结果

AB+∈I*(H)⟺Φ(A)Φ(B)+∈I*(H)
⟺∃c∈R*,∃有界可逆线性或共轭线性算子U∈B(H),U+U=c-1I使得Φ(A)=cUAU+对所有的A∈Ω成立.
3 证明
引理1[8]Φ(0)=0,Φ为单射,且Φ双边保幂等元.
引理2[8]Φ双边保一秩幂等元.
引理3[8]设P,Q∈I1(H),则P⊥Q⟺Φ(p)⊥Φ(Q).
证明 文献[8]已证明结论对于dimH≥4成立,下面证明结论对于dimH=3也成立.我们先证明一个断言:
断言1设dimH=3,P1,P3,P3∈I1(H),则下列条件等价:
(i)P1Pj=0,i≠j,i,j=1,2,3.
(ii)对∀R∈I(H),PiR∈I*(H),i=1,2,3,蕴涵R=I.

证明 设(ii)成立.我们断言:如果i≠j,则rng(Pi)∩rng(Pj)={0}.用反证法,假设H0=rng(P1)∩rng(P2)≠{0},由于P1,P2,P3∈I1(H),故必有rng(P1)=rng(P2)=H0.于是存在H的一组基(不必正交)使得

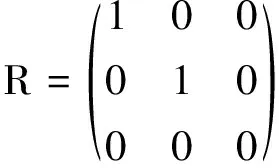
则显然PiR∈I*(H),i=1,2,3,但R≠I,矛盾.
记Pi=ei⊗fi,i=1,2,3,我们断言:{e1,e2,e3}是线性无关的.否则,由前一断言知,H1=span{e1,e2,e3},dim(H1)=2.令R∈I(H),rng(R)=H1,则PiR∈I*(H)但R≠I.
现在验证P1,P2,P3是相互正交的.仍用反证法,假设P1P2≠0,则有〈e2,Jf1〉=α≠0.因为H=span{e1-α-1e2}⊕span{e2-e3},∃R∈I(H)使得rng(R)=span{e2,e3},ker(R)=span{e1-α-1e2},显然Re1=α-1e2,故〈Rei,Jfi〉=1对每个i=1,2,3都成立,此蕴涵PiR∈I*(H)对每个i=1,2,3都成立,但R≠I,又得矛盾.到此,断言1得证.

下面我们给出定理1的证明
定理1的证明充分性显然,下面来证必要性.
情形(1).当H为无限维时,定理1成立.文献[8]中已证明.

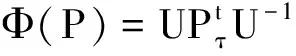
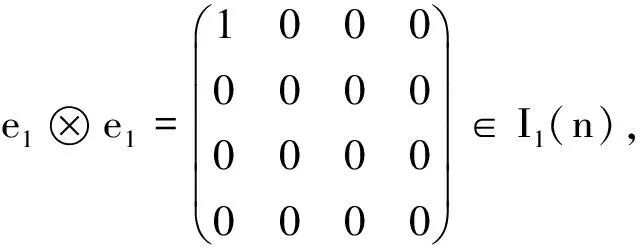
如果Φ(P)=UPτU-1对所有的P∈I1(n)成立,那么
Φ(e1⊗e1)Φ(e1⊗e1)+=U(e1⊗e1)τU-1(U(e1⊗e1)τU-1)+=Ue1⊗(U-1)+e1(Ue1⊗(U-1)+e1)+
=Ue1⊗(U-1)+e1J-1(U-1)+e1⊗JUe1=〈J-1(U-1)+e1,(U-1)+e1〉Ue1⊗JUe1∈I*(n)
所以〈J-1(U-1)+e1,(U-1)+e1〉〈Ue1,JUe1〉=1.

作为现实社会的延伸,网络空间也同样充满了各国之间的分歧和冲突。个别西方国家依靠自己的网络技术优势,垄断网络资源和网络话语权,实施网络霸权。某些西方发达国家为了惩罚或推翻非亲西方的发展中国家,往往会以切断其国家的网络服务为借口进行要挟,逼迫发展中国家就范;或者利用网络空间对于发展中国家进行意识形态渗透,造成社会的混乱;更有甚者直接利用网络工具煽动和策划发展中国家内部的反政府力量进行推翻现有政府的活动。这些活动必然会加深发展中国家与这些发达国家之间关于网络规则、网络秩序和网络治理理念的分歧与对抗。

Ψ(A)=cU+Φ(A)U,(∀A∈Ω)
则对∀P∈I1(n),Ψ(P)=cU+Φ(P)U=cU+cUPτU+U=Pτ,且Ψ(I)=I.对∀A,B∈Ω,AB+∈I*(H)⟺Ψ(A)Ψ(B)+=cU+Φ(A)U(cU+Φ(B)U)+=cU+Φ(A)UcU+Φ(B)+U=cU+Φ(A)Φ(B)+U∈I*(H).故Ψ也满足定理的条件.


由于
则有
设τ(t)=αeiθ1,τ(s)=βeiθ2,其中α=|π(t)|,β=|π(s)|则
所以我们知
α4+2α2β2+β4=1
(1)
又因为
t4+s2=1,所以τ(t)2+τ(s)2=1.从而α2ei2θ1+β2ei2θ2=1
(2)
而式(2)等价于
(3)
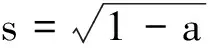
定理1在有限维Hilbert空间可以表述为下面的定理2.

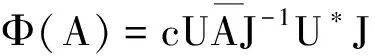
由定理1,我们可以得到以下推论3,其描述了有限维Hilbert空间上保持算子*乘积幂等性的映射.
推论3设n≥3,Ω⊂Mn(C),I∈Ω,C*I1(n)⊂Ω,且∀A∈Ω,Gcv{A,I}⊆Ω.


