一种基于局部和全局拟合的混合多相水平集分割模型及算法

(山东科技大学 计算机科学与工程学院，山东 青岛 266590)

多相分割是近年来图像分割领域研究的新问题。相对于传统的两相分割模型[1-6]将图像分为前景和背景，多相分割方法用多个水平集驱使轮廓线按照一定规则将图像分为多个区域，在处理复杂多目标图像的分割上具有明显的优势[7-9]。将两相活动轮廓模型扩展到多相分割领域，能够显著提升分割效果[10-11]。在水平集方法中，运用多种图像统计信息以及不同能量模型间的加权融合能有效扩大分割能力[12]。Wang等[13]将CV模型[1]与LBF模型结合并扩展到多相水平集，在MR图像分割中取得了不错的结果。Boutiche等[14]将LGD模型[6]和CV模型结合起来并做了改进，在处理灰度不均匀图像和抗噪性上更具有优势。

近年来，基于深度学习的图像分割技术获得广泛关注。Mask RCNN[20]模型是基于Faster RCNN模型架构提出的新的卷积网络，该模型速度更快，在有效检测目标的同时能够完成高质量的语义分割。

医学图像分割需要很高的分割准确度和很强的分割目标性，为了更准确地获得目标轮廓边界并同时处理成像过程带来的噪声，提出一种基于局部和全局拟合的混合水平集分割模型(hybrid multiphase model driven by local and global Fitting energy，HMDLG)及算法,在多相分割框架中综合运用包括梯度、方差、均值多种灰度统计信息检测分割目标，能根据图像区域特性调节分割阈值。实验结果表明，该模型能更加准确地处理目标的拓扑结构。

1 图像分割模型

1.1 拉普拉斯主动轮廓模型

拉普拉斯算子是图像边缘检测的方法之一。Zhang等[15]利用图像拉普拉斯算子与水平集函数结合，能准确的定位弱目标边界。能量项表示为：

(1)

其中，α对噪声起到一个调节作用，Δ是拉普拉斯运算符。上式对应的梯度下降流方程为：

(2)

1.2 LCV模型

Wang等[5]将局部统计信息纳入到CV模型中，以改善对图像局部区域纹理的分割效果，提出了LCV模型。LCV模型的全局项表示如下：

(3)

其中，u0(x,y)表示图像的灰度，c1和c2分别表示曲线内部和外部图像灰度均值。

作为对全局项的修正，LCV模型使用局部统计信息构建局部项，定义如下:

(4)

其中gk是一个k×k大小的均值卷积算子。d1和d2分别是不同图像中gk×u0(x,y)在轮廓线C内外的灰度均值。

1.3 LGDF模型

Wang等[6]利用图像的局部区域信息，提出了基于局部高斯分布拟合能量的活动轮廓模型(LGDF模型)，利用图像的局部区域方差和均值作为灰度信息统计量。

假设在图像区域Ω中，Ωi表示第i个目标区域，Ox是以x为中心的区域，每个子领域Ωi∩Ox的图像灰度概率密度函数为高斯分布，定义为：

(5)

其中fi(x)和σi(x)分别为局部均值和标准差。引入高斯核函数并最小化能量函数可得到：

(6)

2 基于全局和局部能量拟合的HMDLG模型的算法实现

HMDLG模型算法首先预处理图像，然后返回预分割的结果作为初始轮廓。多相水平集由带有局部特性的全局项和局部项加权构成，其中由特征向量加权的拉普拉斯拟合函数和深度自适应分割项组成的全局项能够精确地分割目标边缘轮廓，引入局部均值和方差作为统计量的高斯核函数作为局部项能更好地处理灰度不均匀区域，全局项和局部项的比重由加权函数调节。

2.1 图像边缘的去噪增强和快速预分割

HMDLG模型算法使用多尺度细节提升方法[16]增强图像细节。首先用标准差，分别为σ1=1.0，σ2=1.0，σ3=4.0的3个高斯核函数对原图像I做卷积处理得到3个滤波结果：

(7)

然后用差值提取不同层次的图像细节信息，表示如下：

(8)

最后加权不同的图层信息得到新的图像灰度：

I=(1-w1×sgn(D1))×D1+w2×D2+w3×D3。

(9)

其中w1=0.5，w2=0.5，w3=0.25。

LCV模型中构造了扩展的线性结构张量，易导致边界模糊。因此这里采用非线性扩散张量，在不同的方向上自适应利用不同的扩散系数，在平滑过程中尽可能多地保留图像特征：

(10)

其中，Iσ=I(t,x)*Kρ，Kρ为高斯核函数。结构张量表示为：

(11)

Jρ的两个正交特征向量与相应的特征值分别为υ1，υ2和μ1，μ2。取扩散张量D(Jρ)的特征值为：

(12)

为了降低不同初始轮廓线对结果带来的影响，用基于二维最大熵和改进的遗传算法结合[17]快速获得初始轮廓线。二维最大熵算法采用像素灰度和邻域平均灰度构成的二维直方图搜索阈值，充分利用了像素的灰度分布信息和像素间的空间相关信息获得最佳阈值。改进的遗传算法对选择、交叉、变异等算子进行了优化，运用到二维最大熵算法中大大地减少了计算量，提高了速度。

2.2 HMDLG分割模型的组成框架

HMDLG模型使用双水平集进行四相图像分割，定义水平集函数Φ1，Φ2，分割4个互不重叠的区域：{Φ1>0，Φ2>0}，{Φ1>0，Φ2<0}，{Φ1<0，Φ2>0}，{Φ1<0，Φ2<0}。

模型中Heaviside函数和Dirac函数正则化的表达式如下：

(13)

(14)

其中ε是个小的正常数，Hε(x)和δε(x)的ε取值为1。

在图像域Ω里，四项分割的4个子域用Heaviside函数描述为；

(15)

HMDLG模型总的能量泛函定义为：

(16)

其中，p(Φi)和L(Φi)分别为正则化项和长度项，υ和μ分别为对应的权重系数，εLGLF(Φi)为基于区域的能量拟合项。

区域正则化项p(Φi)：模型使用距离正则化能量拟合项[18]来保持水平集演化稳定

(17)

长度项L(Φi)：模型使用水平集的长度项用来平滑目标轮廓

(18)

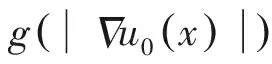
(19)

这里Gσ是标准差为σ的高斯滤波器，m取值为4。代入(18)式中，得

(20)

基于区域能量的拟合项εLGLF(Φi)：使用图像灰度信息构造能量项对目标进行分割。

在HMDLG模型的多相分割的框架中，基于区域的能量拟合项εLGAF(Φi)表示为：

(21)

其中

(22)

式中的ri(i=1,2,3,4)表示由全局和局部统计信息拟合的能量项。

2.3 基于多种局部特征变量加权重构的拉普拉斯全局拟合项

在全局项中，用加权重构的拉普拉斯能量分割目标整体轮廓，并且定位弱边界。HMDLG模型在图像中选取以像素x为中心的P*P邻域，并将其所有灰度值从小到大排列为x1,x2，…,xn, 通过3种特征变量以特定的系数加权组合，得到一组新的数据矩阵u0new(x)作为处理后的图像灰度矩阵:

u0new(x)=MED(x)+τ1IQR(x)+τ2MAD(x)，τ1,τ2∈[0,1]。

(23)

其中，

(24)

IQR(x)=Q3(x)-Q1(x)，

(25)

(26)

在u0new(x)中，中位数信息可以处理图像中的异常值点，四分位距和平均绝对偏差能够锐化目标的弱边界，提高分割精度。将得到的u0new(x)作为拉普拉斯拟合能量(公式2)的输入矩阵，得到：

(27)

2.4 基于深度自适应分割的区域能量全局拟合项

HMDLG模型通过最小化LCV模型的全局项(公式3)，得到梯度下降流方程并改写得到表达式：

(28)

由公式(28)可看出演化过程中LCV模型把轮廓线内外的图像灰度均值(cm+cn)/2作为硬阈值判断水平集演化的方向。HMDLG模型用统计函数min(cm,cn)+λ×abs(cm-cn)近似代替图像灰度值u0,得到新的表达式方程：

(29)

其中λ为分割深度系数，即控制演化偏向于cm和cn的程度，当λ=0.5时，公式(28)和公式(29)的结果近似。在λ的取值过程中，如果人为地根据图像大体估测，并不能取得良好的分割结果，HMDLG模型利用图像的局部和全局统计信息构建了一个统计函数来计算λ：

(30)

其中，cm和cn为轮廓内外的全局灰度均值，fm和fn为轮廓内外的局部灰度均值，α和β为全局和局部的权重系数，且α∈(1,2，…,n)，β∈(0,1，…,n)，ω为补充调节系数。

由于图像存在灰度不均匀问题，如果既要保证对图像细节的分割，又要减少出现过分割或误分割的现象，则需要全局和局部灰度信息的共同调节。HMDLG模型通过构造带有深度系数λ的能量函数来有效调节控制全局和局部统计信息的权重，从而提升分割的精度。

LCV模型的全局项式(29)，LCV模型的局部项以及新的拉普拉斯能量项式(27)共同构建的新能量模型为：

(31)

2.5 基于局部方差和均值统计的局部拟合项

HMDLG模型采用局部高斯方差和均值作为统计量的LGDF模型局部分割项，表示如下：

(32)

2.6 MLGLF模型的梯度下降流方程

在HMDLG模型的多相分割框架中，由式(22)可得基于区域的能量拟合项：

m,n=1,2,3,4。

(33)

其中θ(x)是系数调节方程，图像局部窗口灰度信息计算获得[14]，表达式为:

θ(x)=γaverage(CN(x))(1-CN(x))，

(34)

(35)

式(34)～(35)中，γ是正整数,Mmax和Mmin分别为图像局部窗口最大和最小的像素值。Mg是图像的灰度极大值，取值为255。

式(33)中，图像的局部均值fi(x)和方差σi(x)表示如下：

(36)

(37)

图像的全局均值ci(x)和差分图像均值di(x)分别表示为:

(38)

(39)

其中Mi(x)是4个分割子域，由公式(15)计算得出。

将总能量方程最小化，求解下列两个拉格朗日梯度下降流方程：

(40)

(41)

3 算法实现步骤

HMDLG模型算法首先对分割图像进行纹理增强和去噪，通过预分割得到初始轮廓Φ1和Φ2，然后进行分割。在判断水平集演化是否停止时，通过设定固定的迭代次数并引入一个边界停止函数[19]：当迭代次数大于20次，并且双水平集演化轮廓线同时满足有5个或者5个以上的迭代结果重合时中断演化过程。

HMDLG模型算法的主要步骤如下：

预处理：采用公式(7)～(12)对图像预处理；

预分割：预分割得到初始轮廓Φ1和Φ2；

k=0；

for(i=1;i<=n;i++)

依次通过式(36)～(39)计算ci,fi,σi,di；

通过式(34)和(35)计算θ(x)；

通过式(33)计算rm-rn；

通过式(22)计算S1(x)和S2(x)；

根据式(40)和(41)迭代Φ1,Φ2；

end for

k=k+1；

end while。

4 实验结果与分析

将HMDLG模型应用于医学图像和自然图像分割，并与最新的多相混合分割模型和机器学习模型的分割结果进行比较。实验电脑配置为COREi 7 CPU，8GB RAM。多相水平集实验环境为MATLAB7.10.0(R2010a)，系统为Windows 10，深度学习实验测试环境为Python 3.5,Tensorflow 1.5.0，系统为Ubuntu 16.04。HMDLG模型参数设置：ε=1，σ=3，υ=1，Δt=0.1,μ=0.001×2552，τ1=τ2=0.5。α,β,ω根据图像特点选取。

实验1用一组核磁共振医学图像进行分割实验,将HMDLG模型的实验结果与Wang等[13]和Boutiche等[14]提出的多相分割模型的结果进行对比，如图1所示。

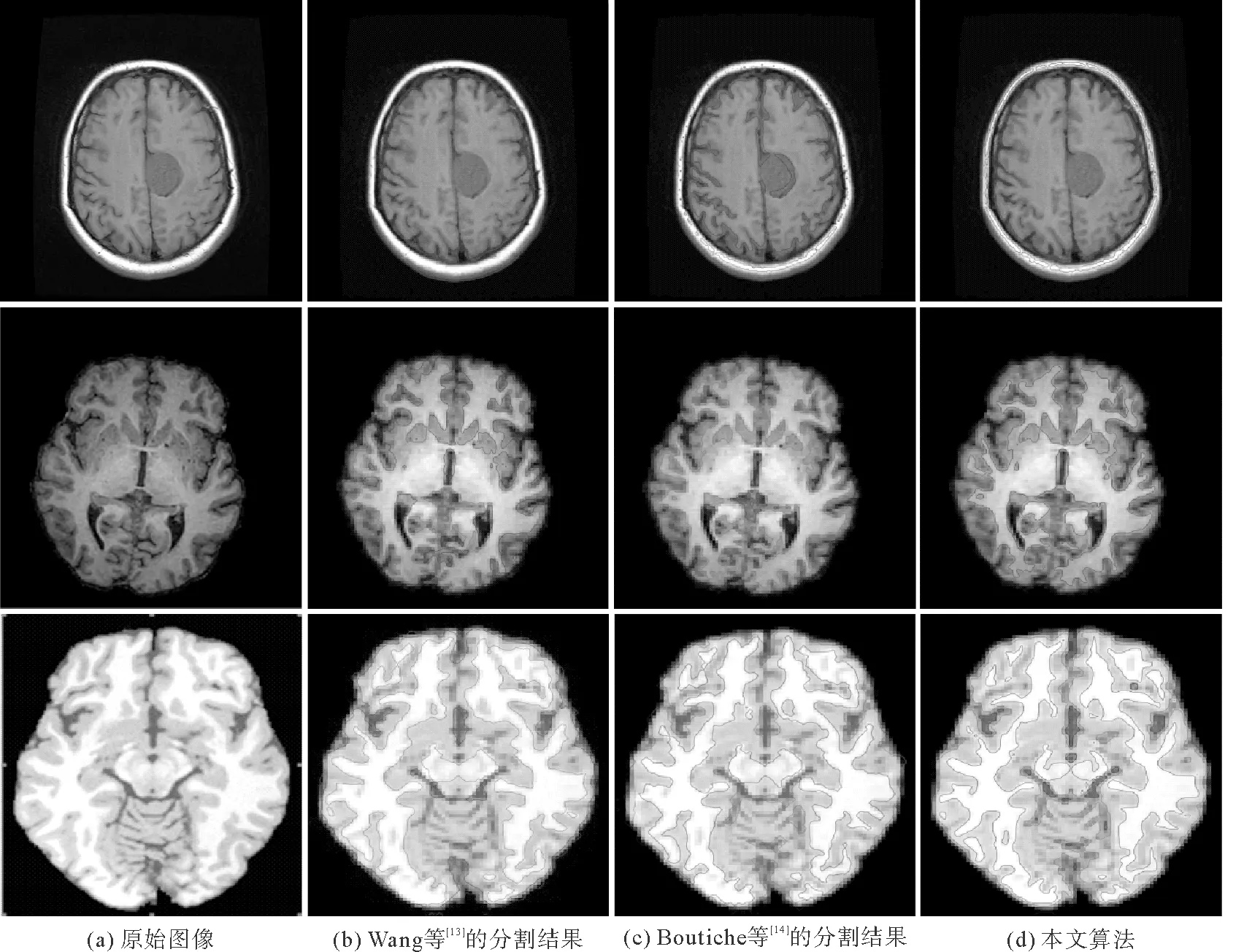
图1 MR图像的分割实验结果 Fig. 1 Segmentation results of MR images

由图 1看出，HMDLG模型在3组MR图像的分割中均取得了最好的结果。3组模型对目标轮廓都能完成有效分割，但是对部分边界和区域的分割效果有差异。Wang等[13]提出的模型使用CV和LBF方法相融合，对图像的局部分割不够细致，特别是对细小组织区域的处理较差。Boutiche等[14]提出的模型局部采用LGDF方法进行构建，在灰度不均匀区域的分割结果更好，但在某些局部区域的分割仍然不够精确。HMDLG模型取得了最好的分割结果，在分割的精细度上领先于其他两组模型。

实验2用一组自然图像的灰度图像继续进行实验，将HMDLG模型的实验结果与深度学习Mask R-CNN模型[20]和Boutiche等[14]提出的多相分割模型的结果进行对比，如图2所示。

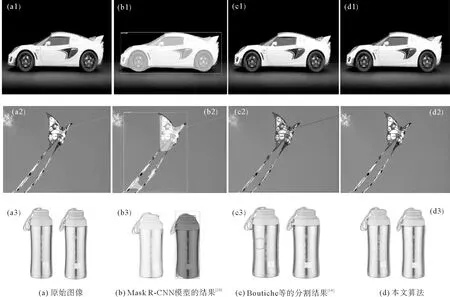
图2 自然图像的分割实验结果 Fig. 2 Segmentation results of natural images

本实验中Mask R-CNN模型使用COCO数据集进行训练，测试图像均来自COCO数据集所属类别的单目标灰度图像。基于深度学习的Mask R-CNN模型通过空间特征量化提取对目标作为整体进行语义分割，能正确地进行目标检测并获取整体轮廓。多相水平集模型对单幅图像的分割速度更快，利用图像灰度统计，函数对目标外部边界和内部拓扑结构分割处理，在后续目标特征分析中发挥更大价值。正确率高。从图2的分割结果可以看出，Mask R-CNN模型对目标边界的定位出现了或多或少的偏差，两组多相水平集模型在目标边界的分割处理上更为精确，但出现了背景区域的过分割现象。其中，HMDLG模型的分割结果最好；Boutiche等[14]提出的模型的分割结果不够准确，比如未分割出车胎，目标内部和背景的处理稍差。

为了衡量各个方法分割精度差异，下面采用定量的方法进行数值分析。采用遗传相似系数(dice similarity coefficient, DSC)作为评价分割精度的指标，原始图像的目标真值通过专家人工分割得到，使用的标注工具为LabelMe，为了避免偶然性，对每一幅图像的分割目标分别由两个实验人员人工勾画三次，取结果坐标的平均值作为目标真值。分割结果由本模型和两组对照实验得到，然后求得各模型与目标真值分割结果的相似系数。DSC指标定义为

(42)

其中S1和S2分别表示目标真值和分割模型的结果(自然图像不考虑背景影响，只计算目标及附近区域)，N(•)表示封闭集合的元素数目。DSC值越接近1，表示分割结果越准确。

上述各组图像的分割实验结果的DSC值如表1所示，表1中3组医学图像与图1中9组图像顺序对应，3组自然图像与图2中3组图像顺序对应。

表1 各图像分割结果的DSC值Tab. 1 The DSC value of all image segmentation results

另外，对于模型中错误分割和未分割的区域，本文采用过分割率OR和误分割率UR来进一步分析:

(43)

(44)

其中，Os表示过分割的图像结果区域，Us表示欠分割的图像结果区域(自然图像不考虑背景影响，只计算目标及附近区域)。表1中的各组图像的结果如表2所示。

表 2 各图像分割结果的过分割率Os和欠分割率UsTab. 2 The over-segmentation rate Os and under-segmentation rate Us of each image segmentation result

从表1和表2中的量化数据可以看出，HMDLG模型与水平集模型的结果对比显示，HMDLG模型对目标内部的分割效果更好，如核磁共振图像内部各组织边界的划分更准确，自然图像目标内部的错分割区域更少；与Mask R-CNN模型的结果对比显示，HMDLG模型的优势在于目标外部的边界的划分，Mask R-CNN模型侧重于目标的检测，语义分割对边界区域的定位更为粗糙。

5 总结

本研究提出了一种混合多相水平集分割模型及其算法，用于分割核磁共振医学图像和单目标自然图像中的灰度图像。水平集模型有效利用了图像区域统计信息和梯度信息，用带有深度系数的区域分割项和多特征变量加权重构的拉普拉斯函数处理复杂的拓扑结构并实现自适应分割，多种能量函数的加权融合有效地增强了模型的鲁棒性。实验表明HMDLG模型适用于需要精确分割的目标图像，并能有效地处理目标的拓扑结构，精确定位目标边缘。