基于层次分析法的铁路旅客换乘方案选择权重研究
2019-11-29刘彦麟吕晓艳周姗琪
刘彦麟,李 琪,吕晓艳,周姗琪,王 梓
(中国铁道科学研究院集团有限公司 电子计算技术研究所, 北京 100081)
换乘方案选择是指旅客在综合考虑不同影响因素的基础上选择的最优方案。很多铁路科技人员针对该问题进行了分析和研究。文献[1]分别给出旅行时间、换乘次数、票价、距离、到发时刻和综合指数6 种影响因素权重的确定方法,提出最短路法和列车匹配法2 种求解方法。文献[2]主要分析影响换乘的各种因素,将这些因素加权为广义旅行时间函数,将换乘方案抽象为最短路径问题。
本文参考文献[1]和文献[2]中的影响因素,在现有运行图的基础上,采用层次分析法(AHP,Analytic Hierarchy Process)对现有的换乘方案数据进行研究,得出各种选择方案的权重,为旅客在换乘方案的选择上提供有意义的参考,同时为铁路部门在运行图的制作和调整方面提供科学依据。
1 层次结构模型
1.1 AHP概述
AHP[3]是美国运筹学家T.L.Saaty 于20 世纪70年代中期提出的,是一种实用的多准则决策方法。其特点是可以对非定量事件进行定量分析,将专家的经验定量化。该方法的基本原理是:(1)将复杂问题分成若干层次;(2)以同一层次的各要素按照上一层要素为准则,进行两两判断,比较其重要性,以此计算各层要素的权重;(3)根据组合权重并按最大权重原则确定最优方案。
运用AHP 的步骤为:建立层次结构模型,构造出层次中的所有成对比较矩阵,计算权向量并做一致性检验,计算组合权向量并做组合一致性检验。
1.2 建立层次结构模型
影响旅客进行换乘行为选择的因素较多,且同一个因素对不同旅客选择的影响也不同,本文选择旅行时长、换乘时段、实际票价、出发时刻、到达时刻5 个影响因素进行分析研究。其中,旅行时长包括列车的运行时长和在换乘站的换乘时长,运行时长指旅客到达时间和出发时间之间的时间差,换乘时长为旅客从一个车站到达另一个车站所用的时长;换乘时段是指旅客进行换乘的时间段,例如,是白天换乘还是夜间换乘;实际票价,为方便研究,这里将票价定义为乘坐铁路交通运输工具所产生的票价之和;出发时刻是指旅客乘坐铁路交通运输工具的出发时刻;到达时刻是指旅客乘坐铁路交通运输工具的到达时刻。
铁路旅客在进行换乘行为选择时,确定各影响因素在心中的相对重要性;根据不同换乘方案的各个特性进行比较对比;将两个层次的比较判断进行综合,选出最优的换乘方案。由此可以看出,铁路旅客换乘行为选择的决策问题可分解为3 个层次,即方案层、准则层和目标层。
本文选择2017 年暑运期间,旅客从太原去往大连,在北京换乘的数据进行研究。由于太原去往大连没有直达列车,若旅客选择乘坐铁路交通工具,需经过换乘才能实现。太原去往北京有动车组列车和普速旅客列车,出发车站有太原和太原南站;从北京去往大连也有动车组列车和普速列车,乘车站有北京和北京南站,旅客可以选择的列车出发时间和到达时间也比较丰富,该数据的选取具有一定的代表性。
根据目前列车的实际开行图,可以供旅客选择的换乘方案有动车组列车换乘动车组列车、动车组列车换乘普速旅客列车、普速旅客列车换乘动车组列车和普速旅客列车换乘普速旅客列车4 种方案。由于旅客经济条件、出行习惯和喜好的不同,其选择的换乘方案也不同。根据影响换乘方案选择的因素和可供选择的方案构造的层次结构模型图[4],如图1 所示。
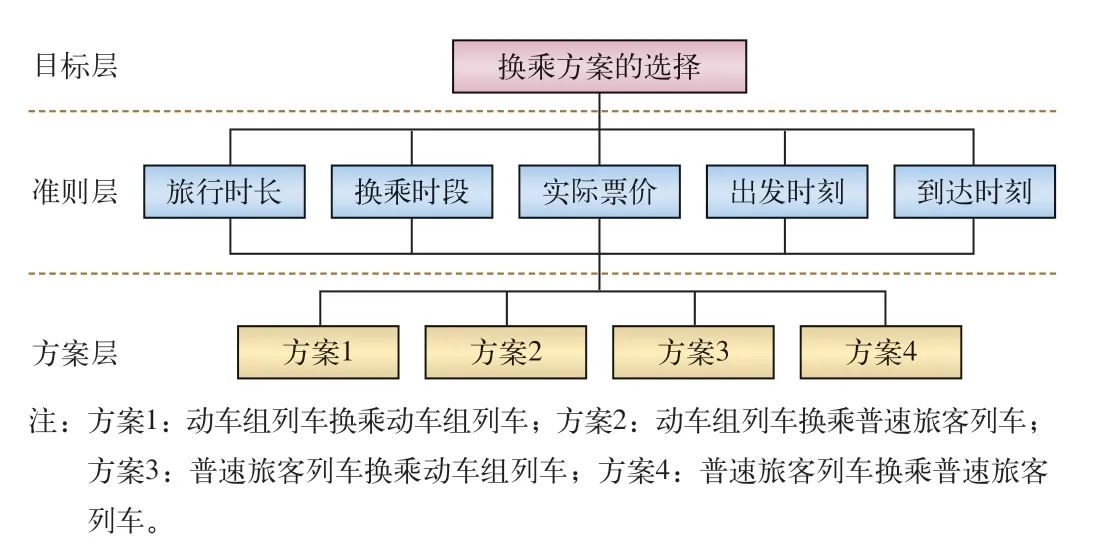
图1 旅客换乘方案选择层次结构模型图
2 换乘方案选择计算过程
2.1 构造成对比较矩阵
在建立旅客换乘方案选择的层次结构后,上下层之间元素的关系就确定了[5]。假设铁路部门提供的运力是充足的,则准则层的5 个因素,旅行时长、换乘时段、实际票价、出发时刻、到达时刻都会对目标层换乘方案的选择产生影响。根据上述分析,利用成对比较法和1-9 比较尺度[1]构建准则层对目标层的成对比较矩阵A,其中,1-9 比较尺度如表1 所示。每次取两个因素i和j进行比较,用aij表示i和j对目标的影响之比,全部比较结果可表示为:

其中:n为影响因素个数;i=1,…,n;j=1,…,n。

表1 1-9比例标度表[3]
通过数据调查,得到太原去往大连换乘方案选择的成对比较矩阵C为:

用同样的方法构造第3 层方案层对第2 层准则层的每一元素的成对比较矩阵Bk,k=1,…,5,针对本文选取的换乘数据,B1~B5表示目前铁路部门提供的太原到大连经北京换乘可供旅客选择的现有方案(方案1、方案2、方案3 和方案4)对应准则层每一元素(旅行时长、换乘时段、实际票价、出发时刻、到达时刻)的成对比较矩阵,如B1表示方案层的4 种方案针对旅行时间的成对比较矩阵。构造的成对比较矩阵B1~B5如下。

2.2 计算权向量并做一致性检验
2.2.1 计算权向量
针对每一个成对比较矩阵,运用特征根法求出权重系数,并将其归一化为同一层中相应指标对上一层某个指标的权重向量[6]。
计算成对比较阵A每一行元素的几何平均值得到近似的特征向量其中:
其中,Vi即为权重系数值,权重向量为V=(V1,V2,…,Vn)T。
2.2.2 一致性检验
在实际应用中,为避免其他因素对成对比较矩阵的干扰,成对比较矩阵需满足大体上的一致性,只有通过一致性检验,才能说明成对比较矩阵可以被接受。本文主要通过一致性指标、随机一致性指标和一致性比率来对矩阵的一致性进行检验。
一致性指标CI可表示为:
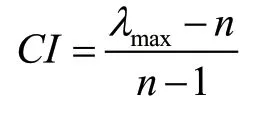
其中,λmax是成对比较阵的最大特征值。
一致性比率CR可表示为:

其中,RI是随机一致性指标,其具体数值可通过表2 查找。

表2 随机一致性指标RI数值表
一般情况下,当一致性比率CR<0.1 时,认为成对比较矩阵A的不一致程度在可接受范围之内,可将其特征向量归一化后作为权向量,否则要重新构造成对比较阵,利用矩阵元素变化与一致性的关系,确定影响一致性的关键元素并进行调整。
2.2.3 实例计算
本文运用Matlab 程序软件[7],基于2.2.1 和2.2.2小节的理论和计算方法,对2.1 节中构造的换乘方案成对比较矩阵进行分析和计算。
(1)准则层对应目标层
运用Matlab 程序软件求得准则层因素对应目标层的成对比较阵C的最大特征值与对应的特征向量为:

将矩阵C的特征向量U归一化得权向量V:
V=(0.273 9,0.480 7,0.052 8,0.094 9,0.097 7)T
因此,矩阵C的一致性指标CI=0.028 675。由于C的阶数为5,由表2 可知RI=1.12。矩阵C的一致性比率通过一致性检验。
(2)方案层对应准则层
对成对比较矩阵Bk(k=1,…,5),计算出各自对应的权向量Vk,最大特征根λk和一致性指标CIk以及一致性比率CRk,结果如表3 所示,其中,vki(i=1,…,4)为权向量Vk的元素。
从表2 中可以看出,对于各个准则元素的一致性比率CRk,均有CRk<0.1,所以权重向量均通过一致性检验。
2.3 计算组合权向量并做组合一致性检验
计算同一层次中所有元素对于最高层(目标层)的相对重要性标度(排序权重向量)称为层次总排序。利用总排序一致性比率进行检验[8],若通过,则可按照总排序权向量表示的结果进行决策,否则需要重新考虑模型或重新构造那些一致性比率较大的成对比较矩阵。

表3 换乘方案选择方案层对应准则层的计算和检验结果列表
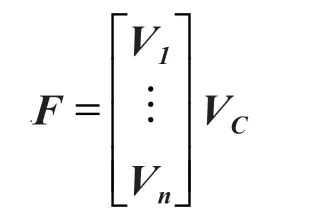
假设准则层的影响因素个数为k,准则层对应目标层的权向量为VC,方案层对应准则层的权向量为V1,V2,…,Vk。则排序权重向量F为:
总排序一致性比率为:
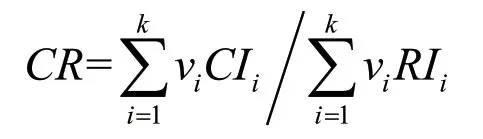
其中,vi为向量VC的元素。
利用上述公式对旅客换乘方案选择的数据进行计算,可得方案对目标层的排序权重向量F和总排序一致性比率CR分别如下:
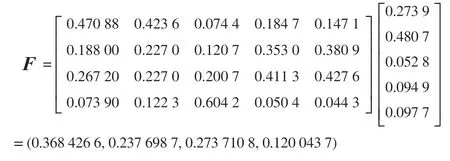
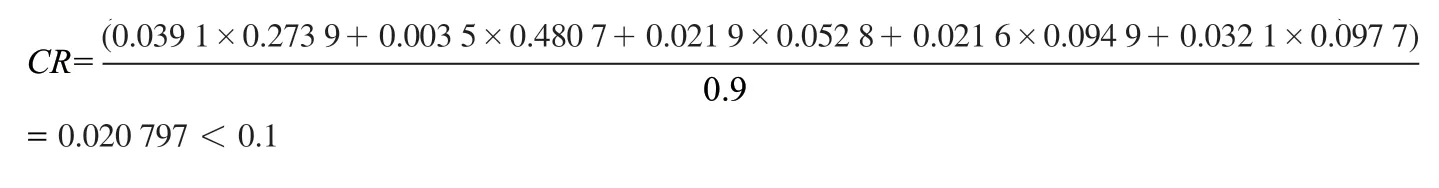
由CR<0.1 可知层次总排序通过一致性检验。(0.368 426 6,0.237 698 7,0.273 710 8,0.120 043 7)可以作为最后的决策依据。即各选择方案的排序权重为:方案1>方案3>方案2>方案4。
通过对2017 年暑运期间,旅客从太原到大连经由北京换乘的数据进行人工验证,得出该方案的计算结果与实际结果一致。
3 结束语
本文应用AHP 对旅客换乘方案的选择问题进行分析,通过将影响换乘方案选择的5 个因素进行量化,得出了旅客换乘方案选择的排序权重,并用实际数据验证其正确性。研究结论为铁路部门在编制列车开行方案和优化列车运行图方面提供了科学的依据,可用于辅助决策。
由于验证数据是抽样选取的,本文的结论具有一定的局限性,且只能说明当前旅客在现有运行图基础上的选择情况。随着高速铁路的不断发展及旅客认知水平的不断变化,旅客换乘方案的选择也会发生相应的变化,因而,评判结果也会有变化。对于这类问题,还有待于进一步探讨和研究。
