平面体系的自由度计算及分析步骤刍议

周海龙　安珍　李平　李昊

摘  要：平面体系的几何组成分析是结构力学与建筑力学课程的教学重点与难点，自由度等基本概念的理解及基本规则的掌握是学好本章的基础，作者根据多年的教学经验，依据学生作业常出现的问题，对自由度的计算给出合理化的公式，并按照“三步走”的思路给出几何组成分析习题规范的解题步骤，对学生掌握好本章内容，养成严谨认真的学习态度具有重要指导意义。

关键词：平面体系;自由度;几何组成分析;分析步骤

中图分类号：Ο342         文献标志码：A         文章编号：2095-2945（2019）31-0032-03

Abstract： The analysis of the geometric composition of the plane system is the teaching focus and difficulty of the course of structural mechanics and architectural mechanics. The understanding of basic concepts such as freedom and the mastery of basic rules are the basis for learning this chapter. Based on years of teaching experience， the author gives a rational formula for calculating freedom based on the problems that often arise in student homework. And in accordance with the "three-step walk" thinking to give the geometric composition of the analysis of the specification of the problem-solving steps， which to master the content of this chapter， to develop a rigorous and serious attitude of learning for students has an important guiding significance.

Keywords： plane system; freedom; geometric composition analysis; analysis steps

平面体系的几何组成分析就是分析若干杆件所组成的体系是几何不变体系還是几何可变体系，有的教材将此过程称为几何构造分析或机动分析[1]，其主要目的就是确定体系能否作为工程结构，工程结构要求体系必须为几何不变体系，另外通过分析体系的内部组成，可以搞清楚杆件部分之间的组成规律，以便选择合理的计算次序，同时也可以给出体系所属具体结构类型，静定结构还是超静定结构，以方便选择不同的计算方法，提高计算的效率[2]。因此，本章内容看似文字偏多，计算内容偏少，但重要性不言而喻，它直接影响后续静定结构与超静定结构的内力计算，一定程度上也决定着你能否将结构力学学通学透的关键环节。基本概念多是本章内容的一个特点，体系分析过程的文字表述也是本章的一个特色，已发表的相关文献[3-6]较多的集中在分析方法与规则利用技巧等方面进行阐述，对于基本概念与规范的分析步骤论述比较欠缺，因此，笔者根据多年的结构力学教学经验，对这两方面的问题，也有些新的体会，在此与学者们交流，以翔读者。

1 容易混淆的几个概念

1.1 刚片与钢片

几何组成分析中，涉及到相关刚片的选择，在书写过程时，很多同学就会把刚片写为“钢片”，部分同学属于笔误，部分同学是由于不理解其本质含义所导致。刚片是体系中任意几何不变部分，它是平面刚体，可以是一根梁，一根链杆，甚至是基础等。通常认为其在力的作用下，内部任意两个质点的距离不会发生改变，刚度无穷大。这是根据本章研究问题的需要引入的一个新概念，这在先前理论力学与材料力学课程中没有涉及，学生在本质理解上有点困难，需要教师将此概念的本质讲清楚;而“钢片”是涉及到材料的具体属性，用钢材制作的构件，它在力的作用下会发生变形，因此是不一样的概念，不能在此处混用。

理解了这两个概念，后期的几何组成分析中铰结点也不会写成“绞结点”，刚结点也不会写成“钢结点”。

1.2 体系与结构

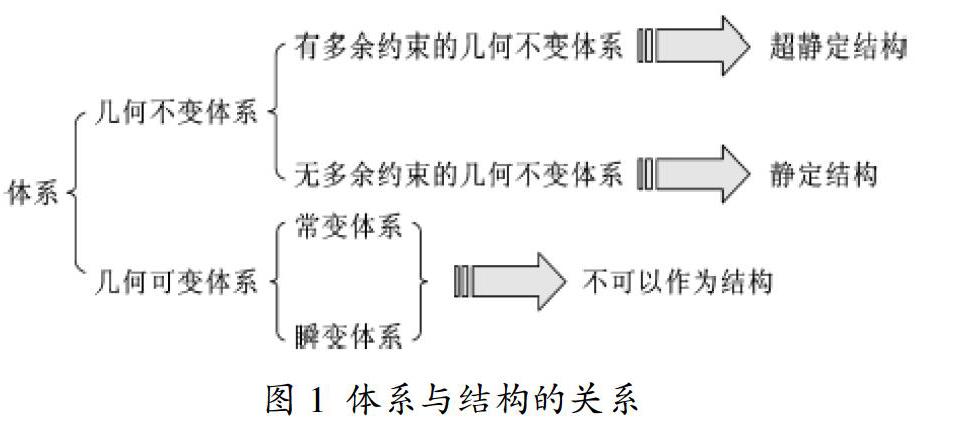
体系是一个广义的概念，有平面体系也有空间体系，结构力学主要研究平面杆件体系，有的体系含有基础，有的体系只是体系本身;而结构是指能够承受荷载而且骨架作用的部分，这两者的关系见图1所示。

理解了这两个概念，在几何组成分析出题时就不会出现“试分析如下结构的几何组成”，结果体系分析的结论为瞬变体系的矛盾表述，实际上老师是要书写“试分析如下体系的几何组成”，概念不清，不够严谨，将会对学生产生误导。

1.3 自由度与约束

体系的自由度是指体系运动时，可以独立改变的几何参数数目，或者是用来确定体系的位置所需独立坐标的数目。因此，在平面内，动点的自由度为2，刚片的自由度为3。

约束是减少自由度的装置，也称为联系。主要的约束形式有链杆、铰结点和刚结点三种。一根链杆相当于1个约束;一个单铰相当于2个约束，一个单刚结点相当于3个约束;复铰与复刚结点要分别转化为单铰与单刚结点;连接n个刚片的复铰相当于（n-1）个单铰，连接n个刚片的复刚结点相当于（n-1）个单刚结点。

理解了这两个概念，为进行自由度的正确计算奠定了基础。

2 体系自由度的计算

体系的自由度计算通常就是指计算计算自由度（W），计算自由度是从计算角度反映加约束前后体系自由度的变化，它是几何组成分析的一个辅助手段。

在应用公式（1）与（2）进行自由度计算时，要注意把握以下几点：

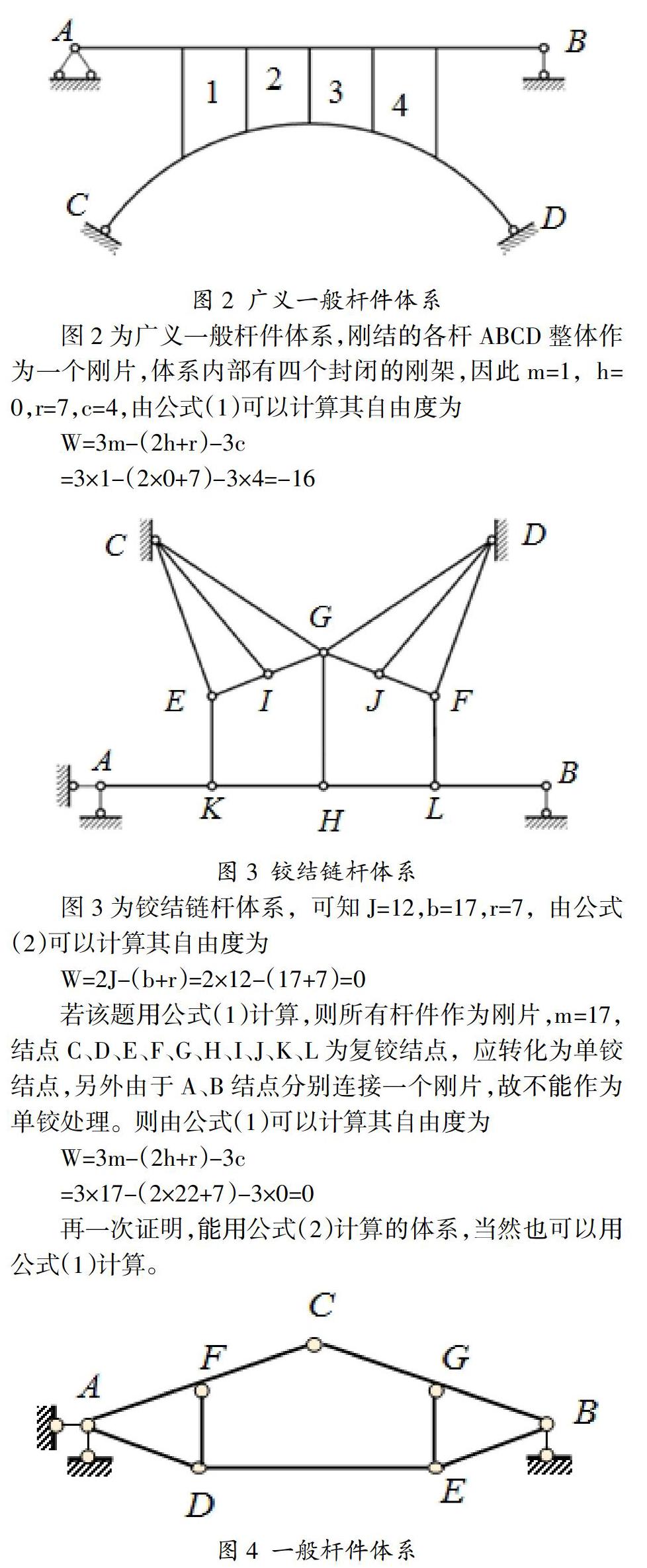
（1）要注意区分一般杆件体系与铰结链杆体系。当体系完全由铰结点连接的杆件组成的体系称为铰结链杆体系（例如桁架）;当体系中有刚结点存在的体系称为一般杆件体系（例如刚架），广义一般杆件体系，本文将其定义为具有封闭刚刚架的体系。

（2）公式（1）中未计入刚结点，是因为当考虑单刚结点时，相应的刚片数也增加;增加1个单刚结点，相当于增加3个约束;相应地，刚片数目也增加1个，相当于增加3个自由度，所以对于整个体系的自由度没有影响。故一般在计算自由度时，不考虑单刚结点，按单一刚片考虑计算体系的自由度。

（3）公式（1）中对于组合结点，计算单刚结点时把铰结链杆当作不存在的，而当计算铰结点数目时，则把刚接各杆看作一个刚片。

（4）公式（1）适用于广义一般平面杆件体系，而公式（2）只能适用于铰结链杆体系，公式（1）的应用范围远远大于公式（2）的应用范围，能用公式（2）计算的体系，当然也可以用公式（1）计算，只不过相对公式（1）而言，公式（2）更加简单一些。

3 平面体系的分析步骤及示例

3.1 分析步骤

（1）计算体系的计算自由度W。若体系中有基础相连，当W>0时体系为几何可变体系;

若无基础相连，当W>3时为几何可变体系。对于W≤0或W≤3的情况，则根据第二步进行分析。

（2）利用几何组成分析的三个规则进行分析。

（3）给出分析结论。对于几何不变体系，应指出有无多余联系，若有，应指出有几个多余联系;若为几何可变体系，可指明是瞬变体系还是常变体系。

3.2 示例

试分析图5所示体系的几何组成。

解：（1）计算体系的自由度

W=2J-（b+r）=2×9-（15+3）=0

（2）进行几何组成分析

如图5所示，由于体系本身与基础通过三根链杆相连，故基础可去掉，只分析体系本身即可。首先将上部二元体B-D-G拆掉，将△ABE作为基本刚片，在此基础上增加二元体A-C-B，C-F-E，得到扩大的刚片Ⅰ。将△EGI作为基本刚片，在此基础上增加二元体G-H-I得到扩大的刚片Ⅱ。刚片Ⅰ与Ⅱ通过铰E与FH链杆相连，由两刚片规则知，原体系为几何不变且无多余联系。

通过上述示例，可以大致总结出几何组成分析过程书写的基本思路是：

（1）基础可否去掉;

（2）二元体能否拆掉;

（3）基本刚片（Ⅰ、Ⅱ、Ⅲ）的选择或扩大刚片（Ⅰ、Ⅱ、Ⅲ）的选择;

（4）刚片之间连接的说明;

（5）规则的说明，采用的是两刚片规则还是三刚片规则;

（6）分析的結论。

学生只要按照以上提纲去书写，就不会出现只有分析结论没有分析过程短短几个字的表述，也不会出现无从下手的感觉，经过一定量习题的训练，相关的原理也会逐渐掌握的比较扎实。

4 结束语

本文选择抽象而难懂的平面体系几何组成分析章节为例进行了阐述，力争通过笔者多年的教学经验，对相关原理及方法进行阐明，首先重点介绍了刚片与钢片、体系与结构、自由度与约束等几个最容易混淆的基本概念;接着对于体系的计算自由度，按照广义一般杆件体系与铰结链杆体系给出了两个计算公式，通过三个示例，介绍了该公式的具体应用;最后给出了几何组成分析的“三步走”步骤，对分析过程的书写也给出了相应的书写提纲，通过示例对分析步骤与分析思路进行了印证，有了方法思路的引导，无从下手的问题将得到根本解决。

参考文献：

[1]李廉锟.结构力学[M].6版.北京：高等教育出版社，2017.

[2]周海龙，李晓丽.建筑力学[M].北京：中国水利水电出版社，2017.

[3]邱秀梅，戴景军，孙建武.平面体系几何组成分析的方法技巧[J].力学与实践，2009，31（2）：80-81.

[4]张琳楠，徐春晖，秦太验.平面体系机动分析的一般方法[J].力学与实践，2014，36（6）：738-741.

[5]郇筱林，王崇革.平面体系几何组成规则的理解和简化分析技巧[J].力学与实践，2018，40（6）：696-699.

[6]孙旭峰.结构力学中的换铰法应用刍议[J].力学与实践，2019，41（1）：91-94.