基于静力学分析的电动拖拉机前桥多目标优化设计

张鑫 葛红恩 赵光龙 王通 杨延超

摘要：为了快速发展25.7 kW电动拖拉机，解决电动拖拉机前桥设计周期长等问题，依据现有SF400E燃油动力拖拉机的前桥，对其进行静力学分析，通过ANSYS对3种工况进行仿真研究，发现该前桥在极限载荷下的最大应力值为372.2 MPa，超出前桥材料Q345的屈服極限7.9%，不能满足电动拖拉机的设计要求;在此基础上对该前桥进行多目标优化设计，优化结果表明，优化后的前桥最大应力值为293.5 MPa，降低了21%，低于前桥材料的屈服极限，优化后的质量为20.1 kg，减少了7%，优化后的前轴能够满足电动拖拉机的设计要求;并对优化后的前桥进行模态分析，模态分析结果表明，优化后前桥的1～6阶固有频率均远远大于来自地面的垂直激励，不会引起共振。

关键词：电动拖拉机;前桥;静力学分析;多目标优化;模态分析

中图分类号： S222.3文献标志码： A

文章编号：1002-1302（2019）18-0247-06

收稿日期：2018-06-14

基金项目：国家重点研发计划（编号：2016YFD0701005）;山东省重点研发计划（编号：2018GGX103002）;山东省研究生教育质量提升计划建设项目（编号：SDYJD17018）。

作者简介：张 鑫（1970—），男，山东泰安人，博士，教授，博士生导师，主要从事机械系统动力学、机电系统建模与仿真、电动汽车设计等研究。E-mail：zhangxinmt@163.com。

通信作者：葛红恩，硕士研究生，主要从事电动拖拉机设计研究。E-mail：sdustjdghe@163.com。

近年来，随着轮毂电机和动力电池技术的快速发展，电动拖拉机将成为发展现代化农机的主要方向。电动拖拉机前轴是拖拉机的关键部件，它不仅是承重桥，还是转向桥，性能要求较高。然而，我国对于电动拖拉机的研究仍不成熟，新的结构需要较长的设计、加工、生产周期以及较高的研制成本，鉴于此类情况，采用在燃油动力拖拉机前轴结构的基础上进行试验、优化的设计方法，能够有效地解决上述问题[1-2]。具体实施方式是将电动拖拉机的设计载荷加载到传统的燃油动力拖拉机前轴上，对前桥进行静力学分析，在此基础上对其进行多目标优化设计，并对优化后的前桥进行模态分析以验证共振影响，最终得到可行的电动拖拉机前桥。

1 前轴静力学分析

25.7 kW电动拖拉机整机质量为2 t，前后轴荷比为2 ∶3，轮距为1.2 m，前桥使用SF400E拖拉机的伸缩套管式前轴，前轴以及前轴臂均由钟型断面的异型钢管构成。与传统燃油拖拉机相比，纯电动拖拉前桥须要承受更大的载荷，如果在设计及后续制造工艺上对此类问题考虑不周全，电动拖拉机前轴则会产生变形或断裂，将严重影响整车的安全性，因此须要对SF400E拖拉机前轴进行静力学分析。

1.1 前轴受力分析

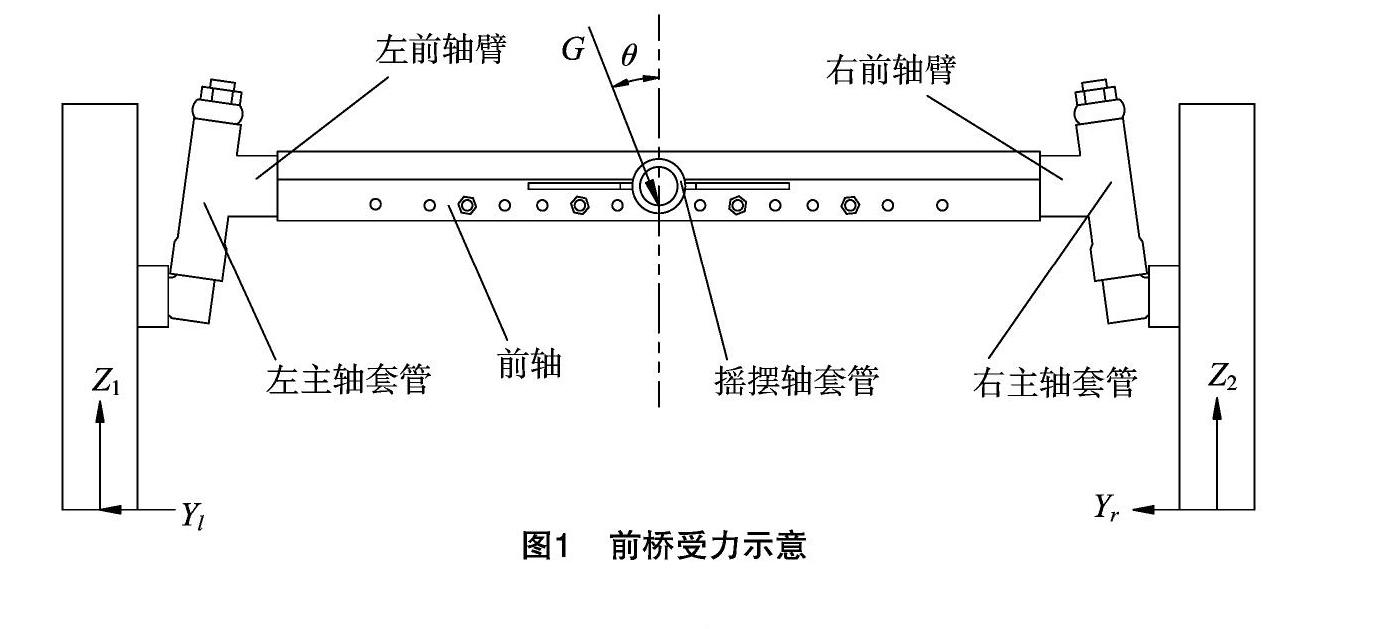
电动拖拉机前桥在行驶过程中不仅承受整体车身的重力、侧向力，而且还有相切方向上的力，受力情况较为复杂，不容易得到实际的受力情况，因此须简化前桥受力。拖拉机结构中非驱动前桥与车架仅靠1根摇摆轴连接，当左、右车轮在不平的道路上行驶和田间作业时，前轴会产生上下摆动，整体车身的重力会与前轴的法线方向产生一定的跳转角θ;当车辆经过颠簸路面时，前轴承受的力不仅仅是整体车身分配到前桥的重力，还会有一定的动载载荷;当车辆在高速前进过程中转弯，前桥还会承受较大的侧向力。由于拖拉机的行驶速度较慢，可忽略转弯侧向力的分析。综上所述，本研究对前轴的静力学分析主要是基于前轴在有动载载荷、跳转角时的受力情况，其受力情况见图1。

对前桥进行受力分析知：

Z1+Z2=Gcosθ;（1）

Yl+Yr=Gsinθ;（2）

G=Kg（m+ml）。（3）

式中：G表示前轴承受载荷;K表示动载载荷;g表示重力加速度;m表示前桥承担质量;ml表示前桥质量;Z1、Z2表示前轮支持力;Yl、Yr表示侧向摩擦力;θ表示跳动转角。

参考农用车驱动桥设计检测标准，驱动桥上限载荷为3倍载荷，即拖拉机前轴的动载载荷K=3。为了不妨碍转向系统的正常工作，一般跳转角要控制在一定的范围之内，本研究设计的最大跳转角为θ=10°。结合以上分析，对前桥进行的强度和刚度分析，主要考虑以下3种工况。

工况1：单倍载荷，即K=1，前轴跳动转角θ=0°;工况2：3倍载荷，即K=3，前轴跳动转角θ=0°;工况3：3倍载荷，即K=3，前轴跳动转角θ=10°。

1.2 有限元模型的建立及其边界条件

本研究采用四面体主导的划分方法，对受力较大的边角处以及零件间的接触面等地方进行网格细化，得到前轴有限元模型共967 968个节点，639 922个单元，网格质量为0.76。

根据不同的工况分别进行加载求解;前轴的试验载荷加载在摇摆轴套管上;约束为左主轴套管固定x、y和z方向的位移，右主轴套管固定x和y方向的位移，z方向自由。材料选用Q345，其材料特性见表1。

1.2 静力学结果分析

按照工况1的受力大小加载求解后，分别提取前桥、前轴、右前轴臂的应力及应变见图2至图5。

整个前桥受力最大的部位集中在前轴臂两端的拳头部位，即主轴套管与前轴臂的连接处上部，此处在实际结构中因作为车轮的支撑，主轴套管与前轴臂的连接位置会产生较大的应力，在主轴套管设计时为满足转向节及转向使用要求时与纵轴轴线具有一定倾角，车轮接受地面的反作用力会产生一定的转矩，因此在横梁与转向套筒连接处产生一定转矩，在上部出现应力集中，由于上部接触角度小于下部接触角，因而上部的圆角半径更小，应力集中更大;另外由于主轴套管与前轴臂的之间存在过渡连接， 前轴与前轴臂的连接处出现较多的相贯线，应力较为容易集中;该前桥是组合结构，是相对薄弱的部位，也造成应力较大。由图5可知，前轴的最大应力点出现在摇摆轴套管较长端的上部与前轴的连接处，原因是在该处的过渡为直角，应力较为容易集中。

由图3、图5可知，前桥在受到应力后，最大综合位移值在摇摆轴套管的最长端处。在摇摆轴套管处施加载荷，使得前轴有较大的应力，应力沿前轴中心处向两边扩散，分析结构特点，由于摇摆轴套管有向下的载荷，同时因地面对车轮的反作用力传至前桥，此时的前桥结构相当于两端固定的简支梁。两端固定后，中间受到力的作用会产生形变，同时由于两端的限定，使摇摆轴套管处产生最大变形量;此外，摇摆轴套管受到均布载荷影响，基于横梁形成悬臂梁结构，随到固定端距离的增加，变形量增加;另外，由于该处受力较大，下端与前轴之间无支撑板，虽然摇摆轴套管左右两边都有肋板固定，但是其限制的主要是左右位移，对于摇摆轴套管上下位移的限制有一定的局限性[3]。

在求解后的工况1的结果中提取前桥及各部件的最大应力和应变值。前桥、前轴、左前轴臂、右前轴臂的最大应力分别约是120.1、43.2、120.1、69.2 MPa，都远低于材料Q345的屈服极限，零件不会发生破坏，前桥能够正常工作;同时根据《汽车驱动桥台架试验评价指标》标明载荷轴每米最大变形量要求小于1.5 mm/m，前桥、前轴、左前轴臂、右前轴臂的最大应变分别约是0.12、0.06、0.06、0.06 mm，取整体应变作为检测数据，最大变形量约为0.092 mm/m，远远低于1.5 mm/m，符合相关标准，该前桥在工况1中满足电动拖拉机的设计要求，即传统拖拉机前桥在承受电动拖拉机的正常载荷时，可以满足其性能需求。

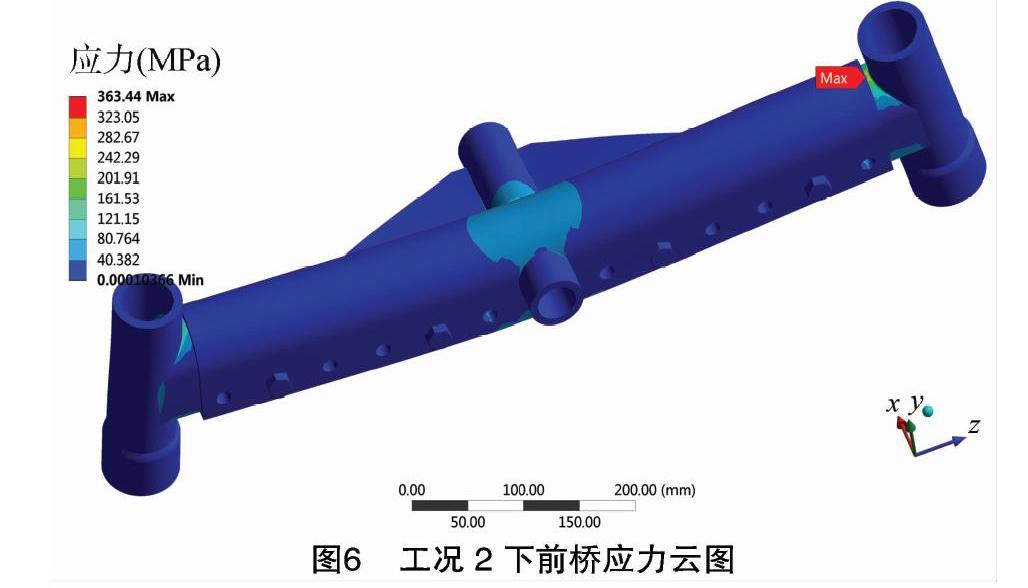
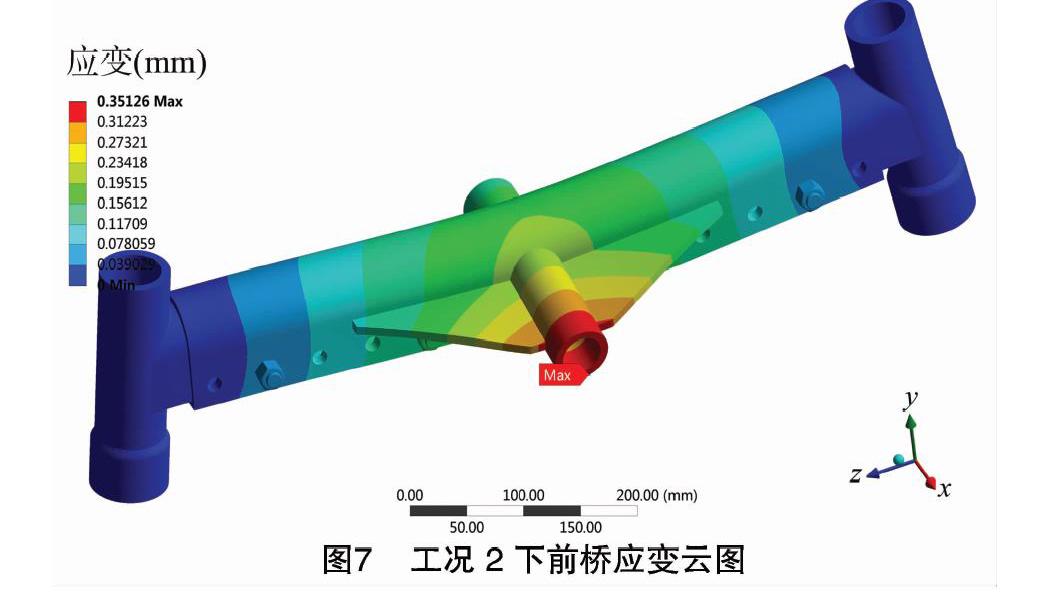
按照工况2、3的受力情况加载求解后，提取2种工况下前桥的应力和应变云图（图6至图9）。在工况2、3的情况下，前桥的应力分布、变形分布与工况1下的应力、应变一致。加载求解后，分别将前桥、前轴、左前轴臂，右前轴臂在工况2和工况3的最大应力值及应变值提取出来，连同工况1的应力值和应变值绘制成戴布拉图（图10、图11）。

由图10可知，前轴在工况2中左前轴臂和前轴的最大应力值不超过材料的屈服极限，但是右前轴臂的最大应力值为363.44 MPa， 超出材料Q345屈服极限的5.3%， 即前桥应力已经超出材料使用要求，该前桥已经发生破坏，不能正常使用。工况3中，除前轴的应力值低于材料的屈服极限外，其他部件均已超出材料的屈服极限，左前轴臂最大应力值为372.2 MPa，超出7.9%，右前轴臂最大应力值372.9 MPa，超出8.1%，2处的应力均使零件发生破坏，不能正常使用。根据相关的拖拉机前桥变形量检测标准，折合到该类型的电动拖拉机上的最大变形为1.8 mm，由图11可知，在3种工况下，前轴的变形量都远远低于1.8 mm，说明该前轴的刚度是满足标准的。

燃油动力拖拉机的前桥在没有经过优化的情况下应用到电动拖拉机上，其刚度在3种工况下都能满足检测标准。其强度在工况1中是满足要求的，但是在有动载载荷和跳转角的工况2和工况3中其部件的最大应力均大于材料屈服极限，零件发生破坏，影响前桥的使用，进而影响整机的性能，该前桥不能满足电动拖拉的设计使用要求。

2 前桥多目标优化设计

由“1.2”节得出结论，传统拖拉机前桥最大应力高于电动拖拉机前桥的设计要求，且局部的应力集中造成零件破坏现象，不能保证其可靠性与安全性。为了使该前桥能够应用在电动拖拉机中，须要对其结构进行优化。对拖拉机前桥进行优化，就是在该结构受到设计极限载荷情况下，即在工况3中，其强度和刚度在满足设计要求的前提下，尽可能地使结构的质量及制造成本降低。

现今的车辆优化设计中，拓扑优化是采用最广泛的优化方式，变厚度法具有使用方便、操作简易等多个优点[4]。在对工程结构进行优化的过程中，一般是把所要处理的物理模型转化成可进行求解的数学模型，再利用数学求解或图解的方式获得最佳解。由分析可确定以下对前桥影响较大的设计变量，P3表示前轴钟型钢管厚度，P4表示前轴臂钟型鋼管厚度，P5表示前轴臂拳部的过渡圆角半径。数学模型为：

minF（x）=f（x）;（4）

X=[P3，P4，P5]。（5）

约束条件：

E=P1<345 Mpa;（6）

TD=P2<0.5 mm。（7）

目标函数：

minG（x）=P6。（8）

式中：P1表示最大应力;P2表示总体变形量;P6表示前桥质量;X为设计变量;E为约束条件1，即最大应力;TD为约束条件2，即总体变形量;G（x）表示目标函数。初步设置设计变量的范围为P3=[5，8]、P4=[5，8]、P5=[1，3]。本研究借助ANSYS Workbench本身提供优化模块-Design Exploration（设计优化）对前桥进行优化。

2.1 灵敏度和响应面分析

局部灵敏度可以直观地反应设计变量对目标结果的影响程度，由于设计变量较多，为了避免盲目的尺寸优化，须对设计变量进行灵敏度分析，以期找出对目标结果影响较大的因素，再对设计参数进行调整，这样能够取得更好的优化效果。

由图12可知，P3、P4和P5对应力P1影响都比较大，P3和P4对整体变形P2影响较大。P3和P4对总体质量P6影响较大，对P5影响极小。圆角能够很好地消除应力集中，但是对于整个结构件的质量和变形几乎没有影响。该优化设计主要考虑的是前桥的强度是否达到标准，可降低设计变量中对应变影响较大，对应力影响较小的设计变量的权重。因此最终优化方案中的设计变量确定为P3、P4和P5。

响应面分析属于1种优化方法，因变量是响应值，单个或多个因素为自变量建立相应的函数关系，从响应面分析中能够很好地确定最终设计变量的范围[5-6]。从图13的响应面分析可知，P3和P4对应力结果的影响较为简单，随着相应参数的增加应力值总体下降，由图14可以看出，P5和P4对应力结果的影响较为复杂，但是可以清楚地看到应力值的最低点出现在圆角半径为2 mm的区域范围内，为接下来P5参数的设置提供依据。

2.2 优化结果及分析

由以上分析可调整设计变量参数设置，结果为P3=[4，7]，P4=[5，8]，P5=[0.5，3]，设计点个数为100，最后优化出3个候选点，即作为本次优化的优化解集，由表2可以看出点2在满足强度的条件下，质量最轻，变形量也能满足要求，故选点2作为本次优化的最优解。圆整候选点参数后的结果为P3=4 mm，P4=6 mm，P5=2.2 mm。

由前文中分析可知，工况3的受力情况最为接近拖拉机的极限工作状态，因此选择工况3作为前后的优化对比。优化前后的参数及结果对比结果见表3。由图8、图9可以看出，由最大应力点和总变形的分布和优化前相同，优化后的最大应力值为293.5 MPa，相比于优化前的应力值降低21%，低于Q345的屈服极限，满足使用要求。最大综合变形为0.39 mm，增加15%，但是远远低于1.5 mm/m，符合国家标准。优化后的质量为20.1 kg，减少整个构件质量的7%。从整体来看，整个结构优化后强度达到设计标准，整体的质量有所减轻，既达到增强结构的效果，又做到轻量化，满足最初的优化目标。

3 Modal分析

机械结构设计过程中，共振或者零件以某一特定的频率振动对零件的破坏是相当严重的。通过对拖拉机前轴的模态分析，能够认识到结构对不同类型的载荷是如何响应的，能够为优化设计提供参考标准，使其结构避免共振。其理论方程为

[M]X″+[C]X′+[K]X=F。（9）

式中：[M]为质量矩阵，X为位移矢量，[C]为阻尼矩阵，[K]为刚度矩阵，F为力矢量。

在求解固有频率和振型时，结构阻尼对固有频率的影响很小，可以不考虑阻尼。简化理论方程：

[M]X″+[K]X=0。（10）

结构在自由振动时，位移函数为正弦函数，即：

X=Asin（ωt）。（11）

式中：A为振幅;ω为角频率。代入式（10）得：

A[K]-Aω2[M]=0;（12）

ω=2πf。（13）

联立上式求得特征值ω2和系统的固有频率f[7-8]。

结合拖拉机前桥的实际安装及受力运动分析，约束左主轴套管x、y和z方向的位移，右主轴套管x和y方向的位移，z方向自由。拖拉机前桥的前几阶固有频率相对较低，对其动力学特性影响较大，因此取前6阶固有频率及其对应振型图作为分析对象。前6阶振型图如图17所示，前6阶固有频率及振型描述如表4所示。

拖拉机在行驶过程中，振动主要来自于地面对车轮的垂直激励，综合汽车以及拖拉机相关文献，地面对于拖拉机的振动频率都是小于100 Hz的。由表4可以看出，前6阶的固有频率远远大于100 Hz，不会引起前桥共振，结构的安全性较高。由前6阶振型图可以看出，1～3阶振型是典型的弯曲振动，4～6阶振动是扭动，最大变形发生在第3阶振型中，最大位移为0.36 cm，部位是摇摆轴套管的端部，由于此部分的受力较大，故在今后设计中须要加固。

4 结论

由静力学分析可知，燃油动力拖拉机前桥应用到电动拖拉机上，在该前桥承受正常载荷时，前桥最大应力值低于材料的屈服极限;在承受极限载荷及有极限跳转角时，最大应力为372.2 MPa，大于前桥材料的屈服极限，强度不够，前桥发生破坏;在3种设计工况下，变形量均远远高于相关标准，刚度达到设计要求。因此综上，该前桥不能满足电动拖拉机的使用要求，须要对其优化设计。

经多目标优化后的前桥在极限载荷及有极限跳转角时，最大应力值为293.5 MPa（<345 MPa），应力值降低21%，优化后的质量为20.1 kg，减少整个前桥质量的7%。优化后的电动拖拉机前桥既满足强度要求，又实现了轻量化。

模态分析结果表明，前桥优化后的各阶固有频率均高于地面的垂直激励，不会引起共振。优化后的前桥能够满足电动拖拉机的使用要求。该试验、优化的方法能够满足25.7 kW 电动拖拉机前桥的设计要求，为设计该类型的前桥提供理论依据。

参考文献：

[1]杨大兴，迟永昊，毕 聪. 轻型两座纯电动轿车车架静态分析与模态分析[J]. 公路与汽运，2012（5）：15-18.

[2]龙海洋. 电动汽车车架模态分析及其优化设计[D]. 唐山：华北理工大学，2015.

[3]李文春，王 斌，刘晓丽，等. 基于ANSYS的果园避障旋耕机旋耕刀片有限元分析[J]. 江苏农业科学，2017，45（1）：193-197.

[4]李 光，王文雅，孙彬青，等. 基于ANSYS Workbench的快装箱多目標优化设计[J]. 包装工程，2016，37（23）：29-33.

[5]Previati G，Gobbi M，Mastinu G. Multi-objective-reliability-based optimisation of a farm tractor front axle suspension[J]. International Journal of Heavy Vehicle Systems，2011，18（3）：257-271.

[6]易 婷，焦志伟，杨卫民. 基于ANSYS Workbench的塑料容器结构尺寸优化设计[J]. 塑料，2017，46（1）：65-67.

[7]沈柳杨，兰海鹏，张 宏，等. 基于ANSYS的核桃分级装置机架静力学及模态分析[J]. 农机化研究，2018，40（7）：36-41.

[8]程彬彬，黄美发，吴常林，等. 基于ANSYS Workbench的龙门铣床横梁多目标优化设计[J]. 组合机床与自动化加工技术，2015（2）：10-12，16.