基于粒子群算法的自动送钻控制器仿真优化
2019-11-28
(西安石油大学 机械工程学院,西安 710065)①
随着石油钻井业向钻井自动化、信息化、智能化方向发展,石油钻机已经由传统人工司钻向自动送钻转变[1]。自动送钻系统不仅可以解放人工司钻因长时间工作而产生的疲劳,更重要的是自动送钻系统在送钻过程中,钻头以恒定钻压钻进,可以提高钻头破碎岩石的效率和速度,减少钻头磨损。自动送钻系统的核心是对钻进过程进行控制,以提高钻井质量和经济效益,降低钻井成本。因此,研究自动送钻控制系统就变得尤其重要[2]。
自动送钻过程由于钻井参数的数据不能实时更新,以及钻井现场工况复杂,自动送钻控制系统因目标函数输入、输出的非线性关系,采用传统的控制器不满足响应时间和精确度等要求,控制效果与理想值相差较大[3]。传统控制器的缺点主要表现在其控制精度不高、抗干扰能力弱,对不同控制对象适应性差等[4]。因此,众多学者相继提出不同的控制方案,其中模糊自适应PID 控制器因其较好的专家控制性能,可以根据控制规则,模拟工作人员判断现场状况并执行控制,得到了广泛的应用。但是,模糊规则的建立过于依赖实际经验,同时模糊参数的调节需要一定的技巧,因此模糊自适应 PID 在很大程度上由于人为的主观性而很难达到理想的控制效果。
为解决上述问题,本文采用粒子群算法优化 (Particle Swarm Optimization ,以下用 PSO 表示)模糊控制器,从而整定 PID 参数。通过该算法的全局寻优的能力,实现自动送钻控制系统的动态性能优化。
1 自动送钻系统数学模型
本文中各参数的含义如表1。

表1 参数含义
液压盘式刹车自动送钻系统的核心部分为电液伺服系统,如图1所示。系统主要由液压泵、溢流阀、节流阀、电液伺服阀、液压缸、刹车钳和刹车盘等组成。自动送钻系统工作原理为:钻头在钻进过程中,由死绳张力传感器处测得的大钩拉力与钻具重力求解所得井底的实时钻压,通过压力变送器将井底钻压与地面给定钻压进行比较,在控制器中对比较结果进行处理,以驱动电液伺服阀对液压缸油压大小的控制,通过杠杆钳对刹车盘进行刹车,进而对钻柱起下钻速度进行控制,以实现恒钻压自动送钻[5-6]。
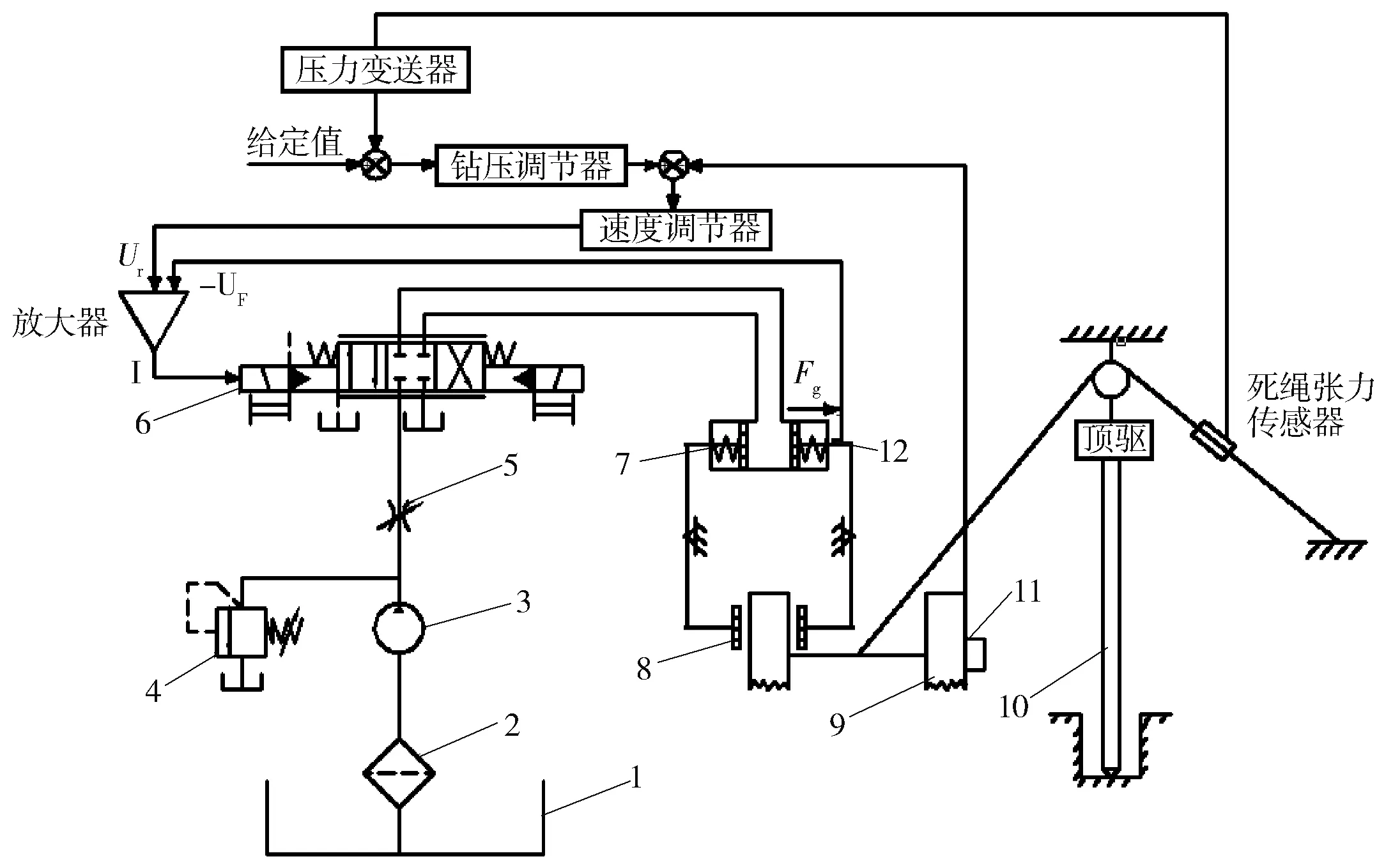
1—油箱;2—过滤器;3—液压泵;4—溢流阀;5—节流阀;6—电液伺服阀;7—液压缸;
由图1可见,液压控制系统主要由放大器、电液伺服阀、液压缸及力传感器等组成,由这些元件组成闭环系统。液压系统的控制过程为由速度调节器输出电压信号Ur与力传感器的反馈电压信号UF进行比较,其差值经放大器输出电液伺服阀电流I,驱动液压缸运行后弹簧输出压力为Fg,直到Ur=UF时,才可保证作用在刹车盘上的力基本为定值。
1.1 液压缸的数学建模
1) 滑阀的流量方程[7]。
QL=KqXV-KcpL
(1)
2) 液压缸连续性方程。
(2)
3) 液压缸和负载的力平衡方程。
Fg=ApL=(ms2+Bcs+K)Y
(3)
1.2 电液伺服阀传递函数
在液压盘式刹车自动送钻控制系统中,电液伺服阀输出流量对输入电流的传递函数可用一阶惯性环来表示[8]。
(4)
1.3 放大器比例环节
放大器在系统中可视为比例环节,则比例放大器和力传感器为
(5)
(6)
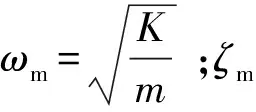
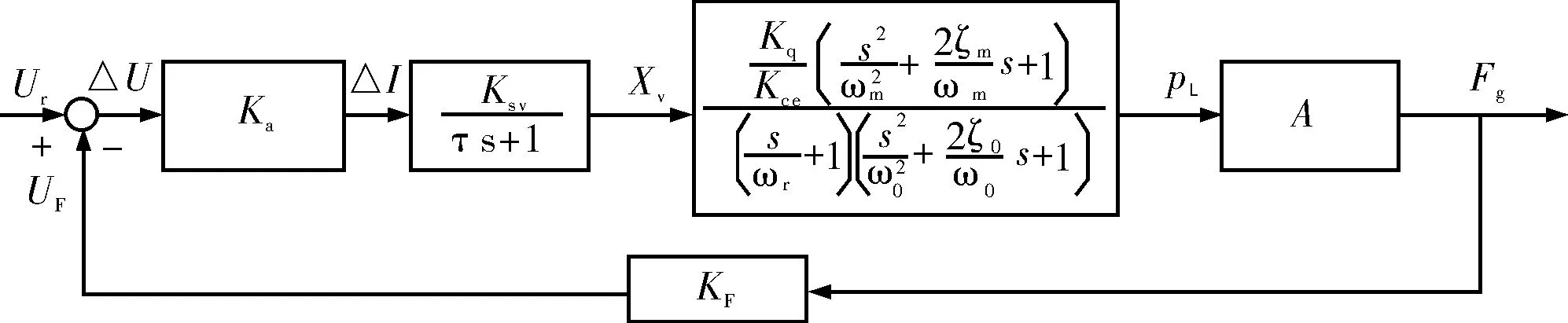
图2 阀控液压缸方块图
综合式(1)~(6),并将表2的数据代入传递函数中,可得:
2 钻机自动送钻系统的控制策略
液压盘式刹车自动送钻控制系统的目标函数具有非线性、时变性等特点,利用传统的闭环控制难以实现控制的精确性和系统的稳定性,为了克服这些缺点,引入模糊自适应 PID 控制器[9]。模糊控制器是一种依赖于专家控制经验来制定相应的控制规则,以实现对常规 PID 参数进行实时调整,从而达到系统的优化控制。
2.1 PID控制器参数整定
PID控制算法的传递函数为
(7)
式中:Kp为比例系数;TI为积分时间常数;TD为微分时间常数。
本文PID控制器参数整定利用临界比例度法。临界比例度法整定过程是先将积分和微分时间常数断开,比例系数从小到大改变数值,直到图像出现等幅振荡的过程,记下此时的比例度δk,等幅振荡周期为Tk=0.019。根据临界比例度法,计算得Kp0=26.65,Ki0=2 805,Kd0=0.063,在进行仿真过程中,当Ki0=800时,系统更稳定。
2.2 模糊自适应 PID 控制器简介
模糊自适应 PID 控制器结构如图3 所示。在控制系统运行过程中,不断检测e和ec与 PID 控制器中Kp、Ki、Kd之间的模糊关系,为了满足e和ec对控制参数的不同要求,根据模糊控制原理对Kp、Ki、Kd进行在线实时修改,实现系统的动、静态性能[10-11]。
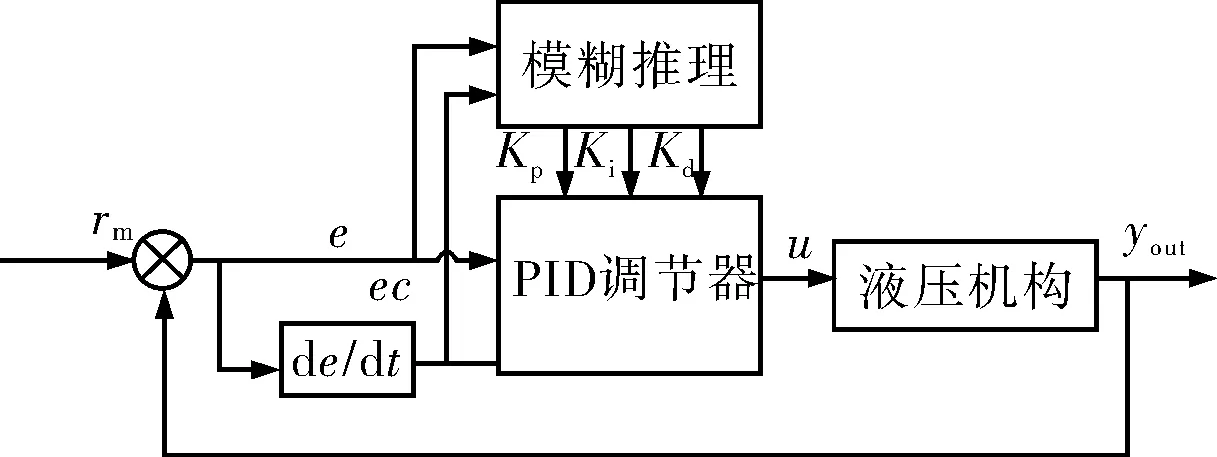
图3 模糊自适应PID控制器结构
2.3 模糊PID输入变量和模糊规则
根据模糊控制器的结构,对 PID 参数的调整实质是一个模糊推理的过程,模糊控制器采用二输入三输出的形式,二输入指的是:输入经过量化的e和ec,其中误差e指的是Ur-UF的差值;三输出指的是:经过模糊规则推理得到 PID 参数的矫正值为ΔKp、ΔKi、ΔKd。根据二输入和三输出,得到模糊子集及其子集元素所表示的数字:{ NB=负大,NM=负中,NS=负小,ZO=零,PS=正小,PM=正中,PB=正大 },再结合它的论域取值范围[-3,3],由此得到输入变量e、ec的量化论域为[-3,3],输出变量ΔKp的量化论域为[-0.3 ,0.3],ΔKi的量化论域为[-0.06 ,0.06],ΔKd的量化论域为[-3,3]。修正后的参数[12-13]由式(8)表示。
(8)
式中:Kp、Ki、Kd是经模糊PID调解后的修正值;Kp0、Ki0、Kd0是模糊 PID 控制器的初始值,它们通过常规 PID 的整定方法得到;ΔKp、ΔKi、ΔKd是经模糊规则调节输出对应 PID 参数的增量值。
根据模糊控制的隶属度赋值表在MATLAB中的Fuzzy工具箱中建立隶属函数曲线,输入变量e、ec的隶属函数曲线如图4所示;输出变量ΔKp的隶属函数曲线如图5所示。其中ΔKi、ΔKd的论域不同,隶属度函数曲线相同。
根据众多学者的分析研究,针对ΔKp、ΔKi、ΔKd3个参数建立模糊控制规则表,如表3。
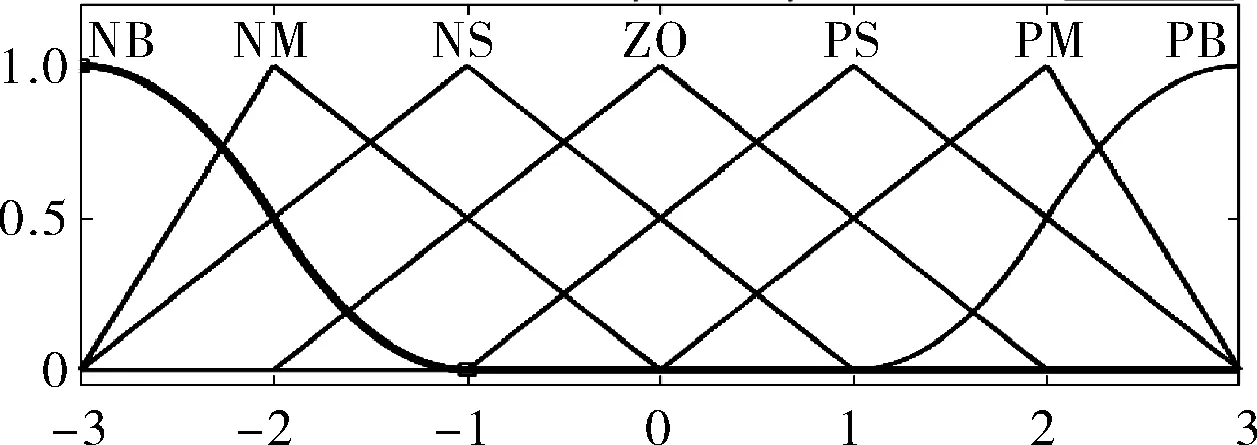
图4 变量e、ec的隶属函数曲线
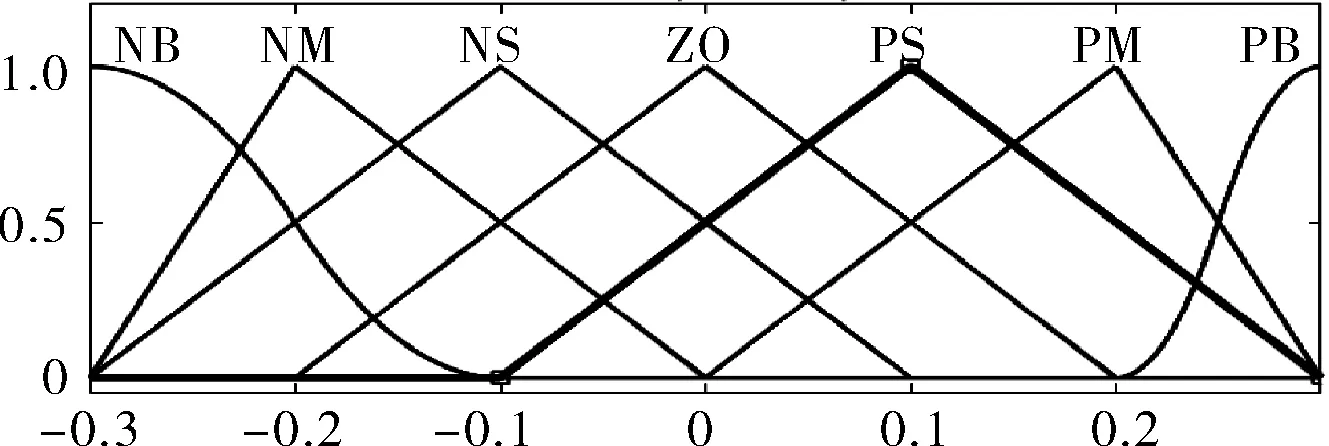
图5 变量ΔKp的隶属函数曲线
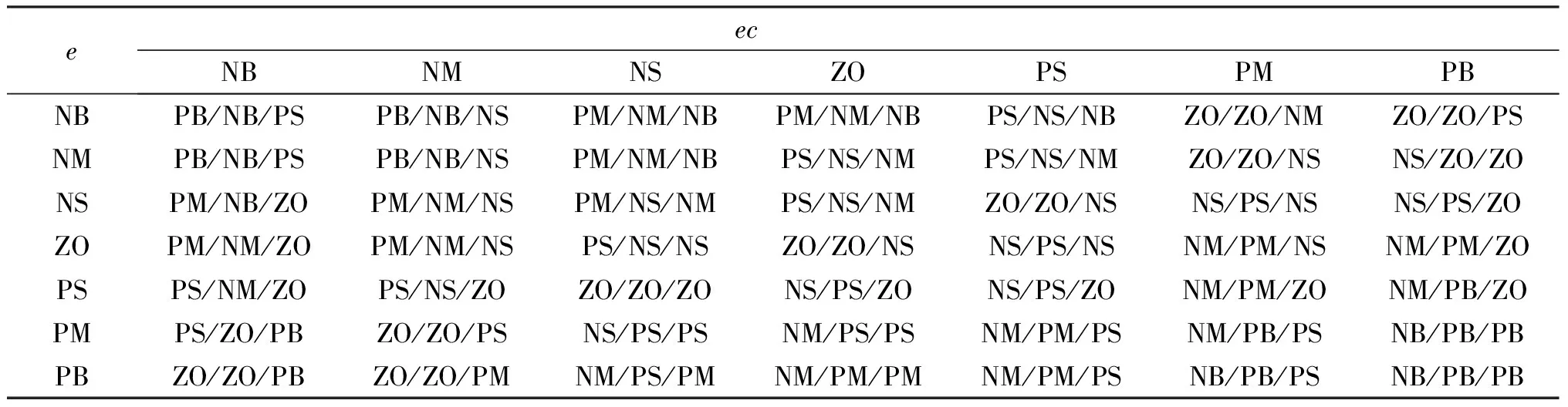
表3 ΔKp、ΔKi、ΔKd模糊规则表
3 基于PSO 优化的模糊自适应 PID 控制器设计
粒子群算法(PSO)是一种智能集群算法,由美国科学家Kennedy 和 Eberhart 设计得出[14]。开发 PSO 算法的核心时通过对鸟群、鱼群和人类社会系统的研究,证实了群体中个体之间信息的社会共享有助于整体优化。
3.1 PSO 优化原理
PSO 是一种随机优化算法。观察结果表明,群体中的个体鸟类或鱼类会受到其他个体行为的影响而移动[15]。 PSO 中每个粒子的速度更新概念如图6所示。在 PSO 的优化过程中,粒子在参数空间中通过3个分量移动:①粒子本身的惯性;②个体最佳的矢量,即粒子本身所发现的最佳位置;③全局最佳的矢量,即所有粒子都找到的最佳位置。通过这个原理,PSO 搜索参数的良好组合,使目标函数达到最佳值。此外,PSO 有一些参数用于采样,例如粒子的数量,常数的值等[16]。
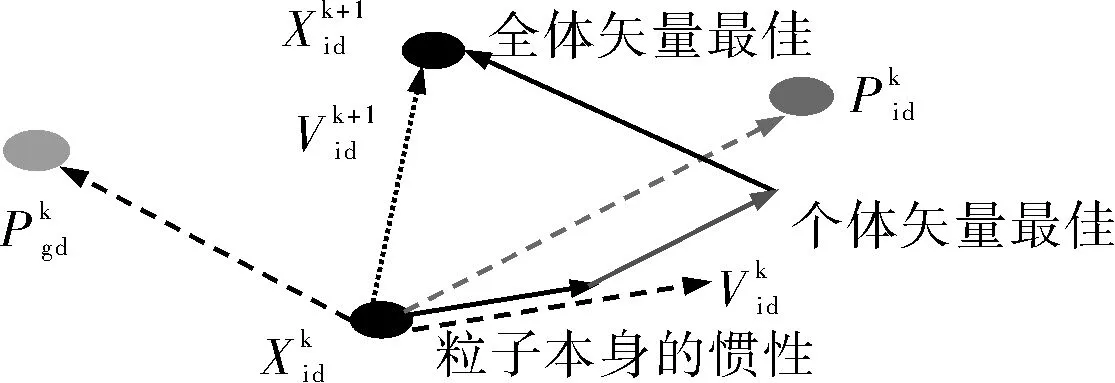
图6 PSO 中每个粒子的速度更新概念
PSO算法进行模糊自适应PID控制器的优化过程如图7所示。
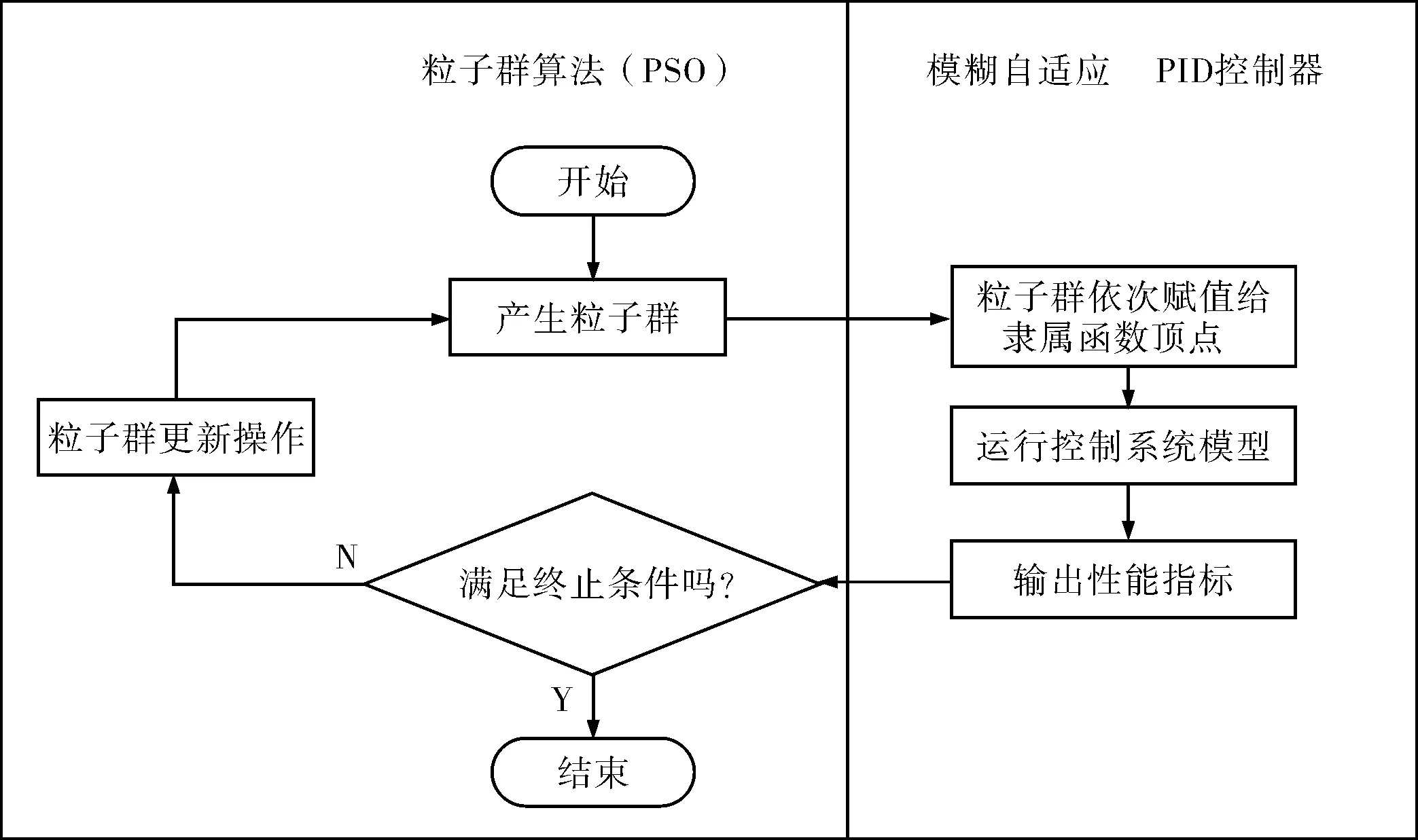
图7 控制器优化流程
对于规模为N,搜索空间为D维的粒子种群,在每次迭代过程中,粒子通过个体极值和群体极值更新自身的速度和位置,即:
(9)
(10)
式中:ω为惯性权重;k为当前迭代次数;Vid为粒子的速度1≤i≤N,1≤d≤D;c1和c2是非负的常数,称为加速度因子;r1和r2是分布于 [0,1] 区间的随机数。为防止粒子的盲目搜索,一般建议将其位置和速度限制在一定的区间[-Xmax,Xmax]、[-Vmax,Vmax]。
3.2 基于 PSO 的模糊 PID 参数自寻优
模糊控制在带入了专家经验的同时也暴露其缺点,就是过于依赖专家经验,即无法满足特殊条件下的抗干扰能力。本文根据对粒子群算法的研究,采用了一种基于粒子群算法优化的模糊 PID 控制算法,该算法弥补了模糊控制器过于依赖专家经验的缺陷。
在寻优过程中,采用式(11)作为每个微粒的适应度函数。
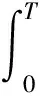
(11)
式中:J为优化的适应度函数;t为仿真时间;e(t)为误差。
4 PSO优化模糊自适应PID仿真
PSO算法进行模糊自适应PID控制器的优化控制框图如图8所示。

图8 控制器优化控制框图
利用 MATLAB 仿真软件,结合文中液压系统目标函数,在目标函数编译的基础上,对基于 PSO 算法优化 PID 的e、ec、Kup、Kui、Kud5个参数进行程序编写,设定 PSO 算法的参数。设初始种群 100,加速因子c1和c2都为 2,粒子最大速度为 1,最小速度为-1, 最大迭代次数为100。在 MATLAB 的 Simulink 模块中搭建系统仿真框图(如图9),将运行程序后得到的e、ec、Kup、Kui、Kud值在系统仿真图中给定,并且在0.1 s处加入阶跃干扰,运行 Simulink 系统,并在 Scope 模块中观察仿真结果。
主要程序为:y_fitness = zeros(1,MaxIter);Kup= zeros(1,MaxIter);Kui= zeros(1,MaxIter);Kud=zeros(1,MaxIter);e=zeros(1,MaxIter);ec=zeros(1,MaxIter)。
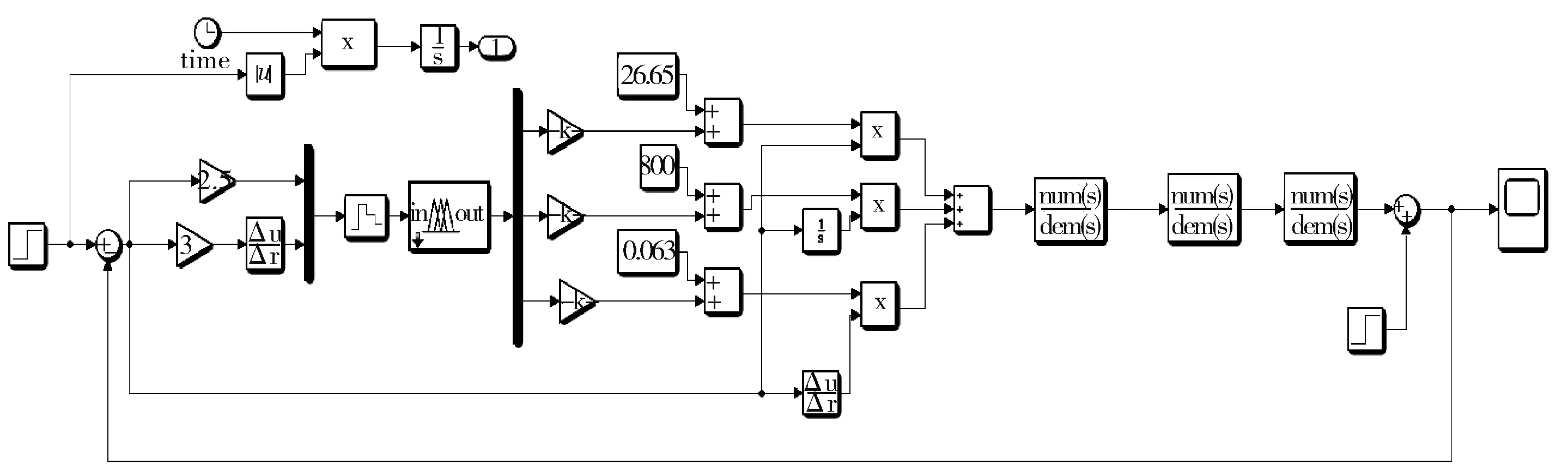
图9 基于PSO算法的模糊自适应PID仿真框图
e、ec、Kup、Kui、Kud的自适应调整如图10~11所示。e=2.5、ec=3;Kup、Kui、Kud的自适应调整值分别为1.17、35.7、0.11。
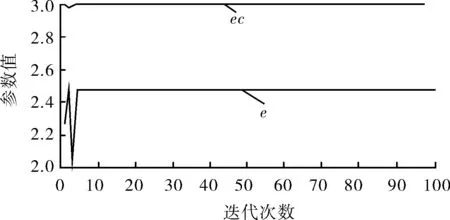
图10 e、ec的自适应调整

图11 Kup、Kui、Kud的自适应调整
粒子群的最优个体适应值如图12所示,为粒子群迭代次数为100次时的适应值。

图12 PSO算法最优个体适应值
笔者同时比较了各控制器的阶跃响应能力和抗干扰能力,如图13所示。其中根据液压盘式刹车目标函数的闭环阶跃响应加了PID 控制器后系统的超调量为20%,且在0.077 s趋于稳定,模糊自适应 PID 控制器的超调量为3%,在0.06 s趋于稳定。本文提出的基于 PSO 算法的模糊自适应 PID 控制系统的超调量为0.1%,响应时间为 0.05 s。
由图13可知,在相同的液压盘式刹车目标函数的闭环阶跃响应时间下,可以发现基于 PSO 算法的模糊自适应 PID 控制系统的响应时间最快,超调量较小,抗干扰能力较强,系统比较稳定,相较于模糊自适应 PID 控制器,其响应时间提高了 0.01 s,并且控制系统较 PID 控制更加稳定,准确,有较好的控制品质,达到了满意的控制效果。
5 PSO模糊自适应 PID 控制器的应用
基于井底钻压的自动送钻系统是利用井底钻压求解地面钻压值,在求解过程中建立模型,并且与软件和基于地面钻压的自动送钻系统集成[17],如图14所示。基于 PSO 算法的模糊自适应 PID 控制器,已经在一种新型的基于井底钻压的自动送钻系统中应用。在整个控制系统中,软件程序的粒子群算法不断优化 PID 控制器参数,并且将更新的参数作用于目标函数中,以实现对基于井底钻压自动送钻系统的完整控制,由控制结果可以看出,系统响应时间较快,整个系统运行平稳,达到了理想的控制效果。
6 结论
1) 根据液压盘式刹车自动送钻系统的工作原理,确定电液伺服阀和液压缸在控制过程中的数学物理方程并确定目标函数,其描述更能体现制动变化过程。
2) 分析了传统 PID 控制器的不足,选定模糊自适应 PID 控制器,针对ΔKp、ΔKi、ΔKd3个参数建立了模糊控制规则表;在 MATLAB 仿真软件中编译了 PSO 算法优化PID 参数程序,并利用 Simulink 模块搭建系统仿真框图,进行系统动态仿真优化。
3) 通过将基于粒子群算法模糊自适应 PID 控制器与 PID控制器和模糊自适应 PID 控制器对比可知,系统的自适应能力显著增强,超调量明显降低,调整时间更短,有较好的控制品质,可以满足自动送钻系统的设计要求,特别适合应用在一种新型的基于井底钻压的自动送钻系统中。
