基于响应曲面分析的卷盘式喷灌机行星齿轮减速箱壳体结构优化

侯新月，张晨骏，汤玲迪，郎景波，陆 静

(1.黑龙江省水利科学研究院，哈尔滨 150080；2.洛阳理工学院机械工程学院，河南 洛阳 471023； 3.江苏大学国家水泵及系统工程技术研究中心，江苏 镇江 212013)

卷盘式喷灌机是一种符合国情并正在成为我国最具发展前景的灌溉装备之一[1]。传统卷盘式喷灌机采用水涡轮作动力，而现有水涡轮结构的效率远低于电机效率，尽管国内学者经过努力，但其效率还是只能达到40%左右[2-5]，是造成卷盘式喷灌机整体动力-传动效率不高的主要原因。因此，采用电机替代水涡轮作动力就自然成为解决其效率问题的有效途径。

由于电机的转速远高于水涡轮转速，使得原来与水涡轮配套的减速箱速比不能与电机匹配，为增加速比，采用普通圆柱齿轮的减速箱需要增加传动级数，这就降低了减速箱的效率。现在，一些国内学者[6-9]采用一级蜗轮蜗杆与二级圆柱齿轮组合，以及采用三级行星齿轮等方案来减少传动级数和提高减速箱效率，取得了一些有益效果，但对减速箱壳体结构未开展研究。在传统的设计中，人们通常使用经验法设计壳体，过度地增加了壳体的壁厚，造成了不必要的材料浪费，增加了壳体的质量[10]。因此，壳体结构的优化设计对于节约原材料和增加减速箱的性能有着重要的意义。

随着各种计算机仿真软件被广泛地运用，人们采用先进方法对壳体轻量化开展了探究。沈伟等[11]通过拓扑优化的方法对小型联合收割机变速箱壳体进行了结构优化;朱剑峰等[12]将变密度法技术引入到汽车变速箱壳体结构设计中；张人会等[13]提出了基于直接自由曲面变形方法的液环泵壳体型线的响应面优化方法；鄢敏丽[14]通过拓扑优化的方法对专用齿轮箱进行了轻量化研究。本文拟采用曲面响应分析方法，对卷盘式喷灌机三级行星齿轮减速箱壳体进行轻量化设计。

1 壳体的静力分析

1.1 壳体几何

如图1所示为三级行星齿轮及壳体的几何模型。因壳体上分布着各种孔及圆角、倒角等小结构，增加了优化的复杂性，故对壳体做出如下简化[15]：

(1)忽略孔及圆角、倒角等小结构。

(2)保留前盖、机体和底座，并将这三部分看成一体。

(3)为保证连接处的强度与内部强度的一直性，将壳体的连接处当成理想连接。

图1 三级行星齿轮及壳体几何模型Fig.1 Geometric model of shell

1.2 模型的加载与求解

采用Workbench自带的Patch Conforming法进行网格划分，自动生成四面体网格，网格尺寸为10 mm，划分网格后壳体模型节点个数为253 608，单元个数为163 077。壳体的材料属性如表1所示，壳体网格划分模型如图2所示。

表1 壳体的材料属性Tab.1 Material properties of shell

图2 壳体网格划分 图3 壳体载荷约束图 Fig.2 Mesh model of shell Fig.3 The load and constraint chart of shell

因在行星传动中，太阳轮、行星轮、行星架这三者对传动轴径向合力为零，故只需考虑各级齿圈对壳体的作用力[16]。将该作用力转化为施加在壳体与齿圈接触面上的扭矩，并给壳体附上一个重力载荷。而在实际工况中，壳体是通过底座上的地脚螺钉固定，故在静力分析之前需对底座进行完全约束[17]。图3为壳体载荷约束图，其中A、B为对底座的约束，C、D、E分别为第一级、第二级和第三级内齿圈对壳体作用转化后的扭矩，F为施加的重力。

经过计算求解，壳体的形变云图和应力云图如图4和图5所示。

图4 壳体形变云图Fig.4 Deformation cloud chart of shell

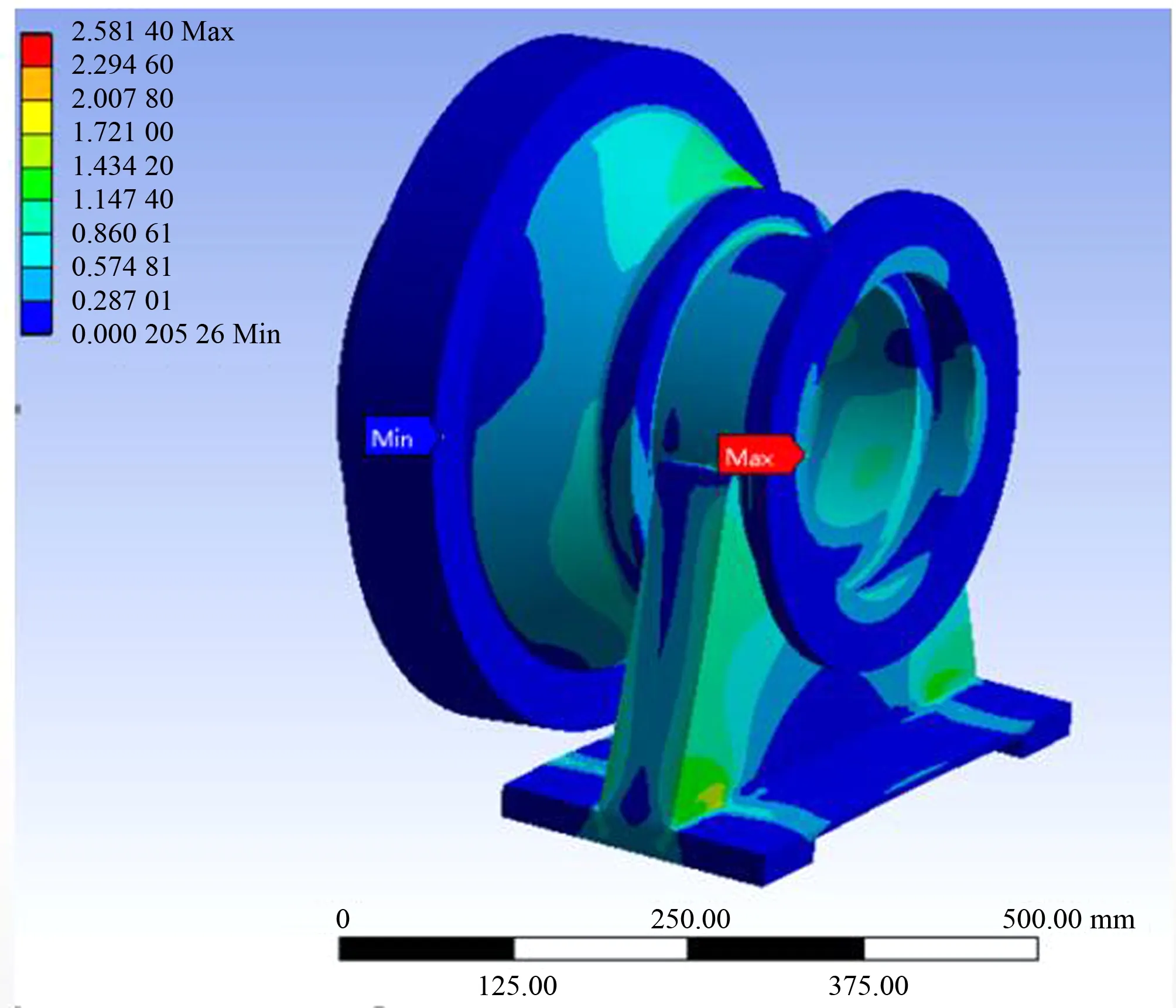
图5 壳体应力云图Fig.5 Stress cloud chart of shell

1.3 结果分析

如图4和图5所示，壳体最大形变为0.045 738 mm，在后盖与壳体中部的连接处，对壳体结构影响较小；壳体最大应力为2.581 4 MPa，位于第三级行星齿轮处的箱壁处，且明显看出壳体应力分布不均匀，且远小于材料许用应力135 MPa。

由此可见，在传统设计中，为了满足设计工况，壳体的壁厚常常被过度地增加，造成了不必要的材料浪费。

2 壳体结构的尺寸优化

2.1 响应曲面分析方法

响应曲面分析方法是基于合理的试验设计并结合实验所得一定数据，构建模型进行拟合，以得出最优组合解[18]。其常用的二阶多项式响应曲面模型如下式，并采用最小二乘法以求其待定系数。

(1)

式中：f(X)为预测响应值；α0、αi、αii分别为偏移项、线性偏移和二阶偏移系数；αij为交互作用系数；Xi为自变量试验水平实际值。

2.2 壳体结构优化模型

设计变量：在保证壳体内部形状不变，仅改变壁厚的前提下，选取对壳体影响较大的4个尺寸作为设计变量：前盖壁厚H1，壳体中部壁厚H2，壳体后端壁厚H3和底座肋板壁厚H4，如图6所示。设计变量初始值及上下限如表2所示。

图6 壳体尺寸示意图Fig.6 Dimensional sketch of shell

mm

目标函数：在保证各部件之间不发生干涉，减速箱能平稳运行情况下，壳体质量最轻，记为f(X)=Mmin。

约束条件：在取安全系数为2的情况下，壳体所受最大应力小于等于材料许用应力135 MPa。

2.3 壳体优化

通过利用ANSYS Workbench软件中的响应曲面优化模块对壳体的结构尺寸进行模拟分析，并根据设计变量的数值及设计变量的上下限，采用中心复合设计法确定了26个试验点，在每个试验点又进行求解，得到该点处箱体质量P5、最大形变量P6和最大应力P7(见表3)。

表3 求解结果Tab.3 Calculating results

优化后，获得了各设计变量对目标参数影响的响应曲面如图7～图9所示。其中，H1、H2对壳体质量影响最大，H1、H3对壳体最大变形量影响最大，H1、H3对壳体所受最大应力影响最大。

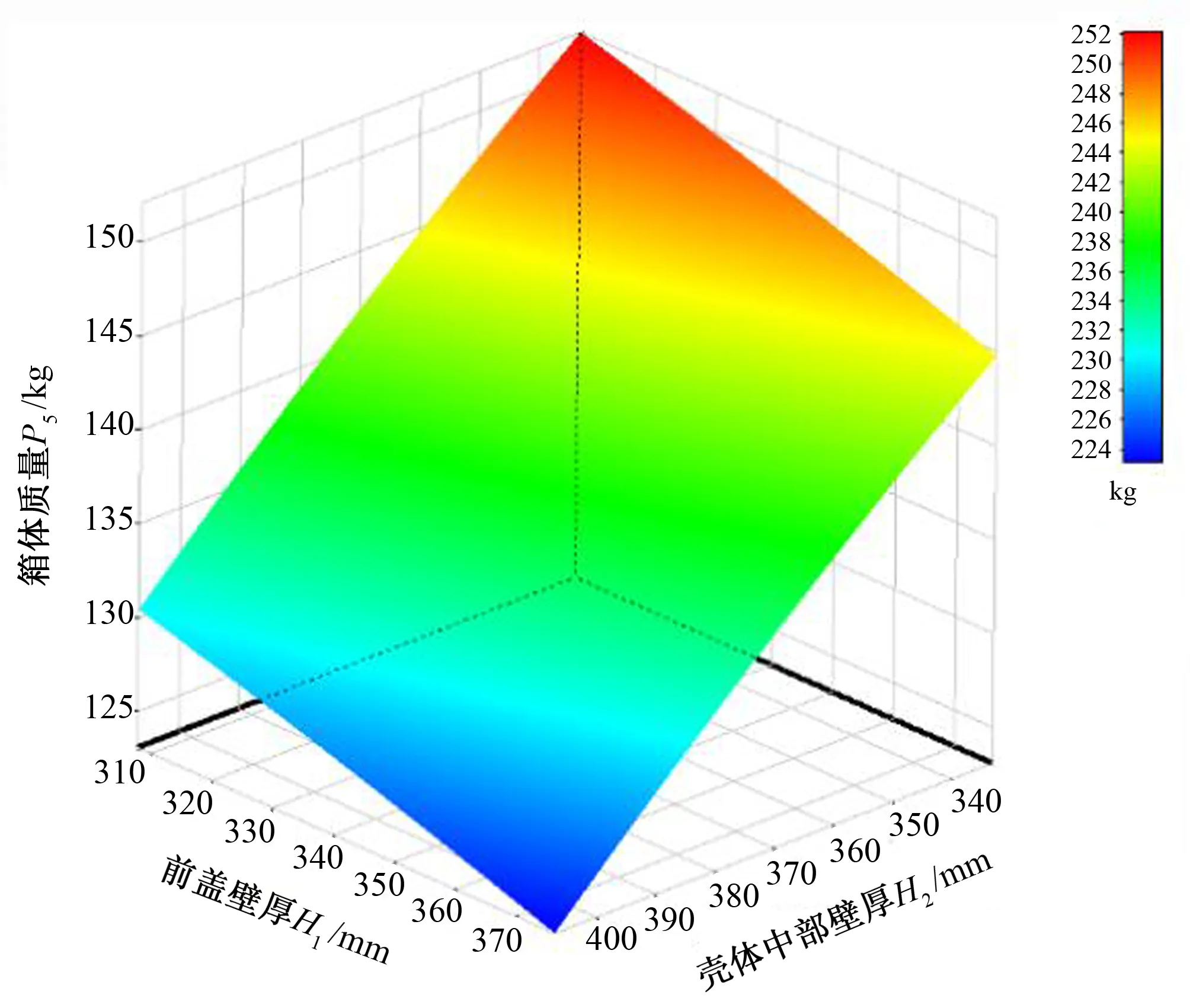
图7 H1、H2对壳体质量的响应曲面Fig.7 Response surface of H1 and H2 to gearbox mass

图8 H1、H3对壳体最大变形量的响应曲面Fig.8 Response surface of H1 and H3 to maximum deformation of gearbox

图9 H1、H3对壳体所受最大应力的响应曲面Fig.9 Rresponse surface of H1 and H3 to the maximum stress on the gearbox

3 结果分析

将箱体的最小质量、最大形变量、最大应力三者进行综合考虑，选取Candidate A为设计尺寸，并将壳体优化进行静力学分析，其优化后壳体形变云图如图10所示，壳体应力云图如图11所示。

图10 壳体形变云图Fig.10 Deformation cloud chart of shell after optimization

图11 优化后壳体应力云图Fig.11 Stress cloud chart of shell after optimization

优化后壳体最大形变量减小，壳体形变对三级行星齿轮组啮合稳定性的影响降低，最大形变量仍在第三级行星齿轮组安装处，与优化前位置吻合。同时优化后最大应力到2.575 MPa，下降了6 400 Pa，且满足强度要求，从优化后应力云图可以看出，壳体在三级行星齿轮安装处所受应力分布均匀，最大应力点转至底座肋板处。

优化后减速箱壳体最大形变量和所受最大应力均减少，刚度和强度都有所提高，同时壳体质量也有所降低，表4为壳体优化前后对比图。

表4 壳体优化结果Tab.4 Optimization results of shell

4 结 语

(1)本文通过对减速箱壳体进行几何建模和对模型进行静力分析发现，传统设计法易造成壳体的壁厚过厚，增大的壳体的质量。

(2)通过Workbench中曲面响应优化模块对壳体进行尺寸优化，前后对比后发现，壳体的质量从138.4 kg下降到127.6 kg，减少了7.8%，同时壳体最大形变量减少，而且应力分布更加均匀合理，壳体的结构更加合理。