基于图像处理技术的微灌砂颗粒形状参数分析

刘清霞，李国强，李景海，翟国亮，靳正轩，邓 忠

(1.安阳工学院 土木与建筑工程学院，河南 安阳 455000；2.安阳市第一中学，河南 安阳 455000； 3.中国农业科学院农田灌溉研究所，河南 新乡 453002；4.安阳工学院 机械工程学院，河南 安阳 455000)

在微灌系统中，砂过滤器是最常用的过滤器之一[1]，而在砂过滤器中，常将石英砂作为过滤介质，因而对砂滤层特性的研究非常重要。董文楚[2]将砂颗粒形状系数定义为砂颗粒不规则粒径(即筛分直径)与等体积球体直径的比值，并进行了相关研究，并对砂滤层过滤机理和堵塞过程进行了分析[3]； Wenquan Niu[4]等对砂滤层物理堵塞做了进一步研究；翟国亮[5]等配制粉煤灰水进行过滤，研究了砂滤层过滤出水浊度的变化规律；Tarjuelo[6]等提出砂过滤器在节水的同时，也应注重节能，从而为下游管网提供充足的水压；Bové[7,8]等研制了一种新型滤帽，并对过滤器水头损失进行了模拟；张杰武[9]等自行配制黄河水，对砂滤料过滤水头损失、出水浊度等性能进行了测试；蔡九茂[10]等对砂过滤器水动三向阀性能开展了对比试验。李景海等对砂滤层清洁压降进行了研究，计算出了最佳过滤速度[11]，并对砂滤层的反冲洗进行了三维模拟，得出了合理的反冲洗速度范围[12-14]。但由于没有考虑砂颗粒形状对过滤效果的影响[15]，得出的理论值与试验值尚有一定误差。

目前，在微灌领域对砂滤料形状特征的研究较少，但在化工和建筑等领域，有不少对颗粒形状的研究，朱继承[16]等对催化剂形状系数进行了研究，涂新斌[17]等采用图像分析技术对颗粒形状参数进行了描述，石崇[18]等对岩土颗粒形状参数进行了分析。

在借鉴上述研究成果的基础上，笔者利用计算机图像处理技术对微灌石英砂颗粒的图像进行处理，得到了砂颗粒面积、周长、外接圆半径和内切圆半径等参数，在此基础上计算了砂颗粒等效直径、简化延长指数和布拉斯谢克系数，通过对砂颗粒形状参数的分析，研究砂颗粒大小分布的均匀性和颗粒形态，为砂滤料的选型和加工提供技术参考。

1 微灌石英砂颗粒形状参数

石英砂颗粒在空间为多面体，其形状具有不规则性和随机性，在平面内则呈现为形状各异的不规则多边形。砂颗粒的形状特征，直接影响到砂滤层孔隙大小及其分布，从而对滤层过滤效果产生重要影响。

砂颗粒的形状也称为颗粒的粒性，颗粒粒性用于描述石英砂颗粒单元体的几何性[19]。在二维平面内，表征砂颗粒形状特征的参数主要有面积、周长、等效直径、外接圆半径和内切圆半径。

在砂颗粒的形状参数中，面积A和周长P属粒径参数，是影响颗粒形状的重要参数。在面积确定的情况下，周长不同则砂颗粒形状不同。同理，在周长确定的情况下，面积不同则砂颗粒形状也会有差异。

颗粒的延性即颗粒的伸长属性，延性系数反映颗粒总体上是长条状、柱状、板状还是近等轴方形形态。采用简化延长指数IA和布拉斯谢克系数Icb评价砂颗粒单元形态[20]。

简化延长指数IA为：

(1)

式中：Ri为砂颗粒内切圆半径，mm；Rc为砂颗粒外接圆半径，mm。显然，IA位于区间[0，1]，当IA取0时，表示砂颗粒为线段，当IA取1时，表示砂颗粒为圆。

布拉斯谢克系数Icb为：

(2)

式中：A为砂颗粒面积，mm2；P为砂颗粒周长，mm；Icb的取值范围为[0，8/π2]，当Icb取0时，表示砂颗粒为线段，当Icb取8/π2时，表示砂颗粒为圆。

显然，在面积A、周长P、内切圆半径Ri和外接圆半径Rc已知的前提下，就可以对砂颗粒形状特征进行计算分析。

2 砂颗粒图像处理方法

计算机图像处理技术为砂颗粒形状特征参数的获取提供了方便途径。其原理是通过高精度数码相机获取砂颗粒的数字图像，然后利用图像处理软件(如Adobe Photoshop)或自编程序，根据砂颗粒灰度与背景灰度的差异，将砂颗粒从图像背景中分离出来，对图像进行分析、加工、处理和数据输出。颗粒在二维平面内的面积A、周长P、内切圆半径Ri和外接圆半径Rc等形状参数可以从图像直接提取，参数及描述见表1。

表1 石英砂颗粒形状参数表

以粒径范围为1.0～1.18 、1.18～1.4和1.4～1.7 mm的3种滤层为研究对象，每种滤层中各随机取16粒石英砂作为样本，采用高精度数码相机对砂颗粒样本逐一拍照(示例见图1)，然后采用计算机C语言编制程序，从而对砂颗粒图像进行分析处理。

图1 石英砂颗粒数码图片示例

3 砂颗粒形状参数计算与分析

3.1 形状参数的计算

采用编制的计算机程序，对石英砂颗粒数码图片进行处理，得到砂颗粒的形状参数A、P、Ri和Rc，计算框图如图2所示。

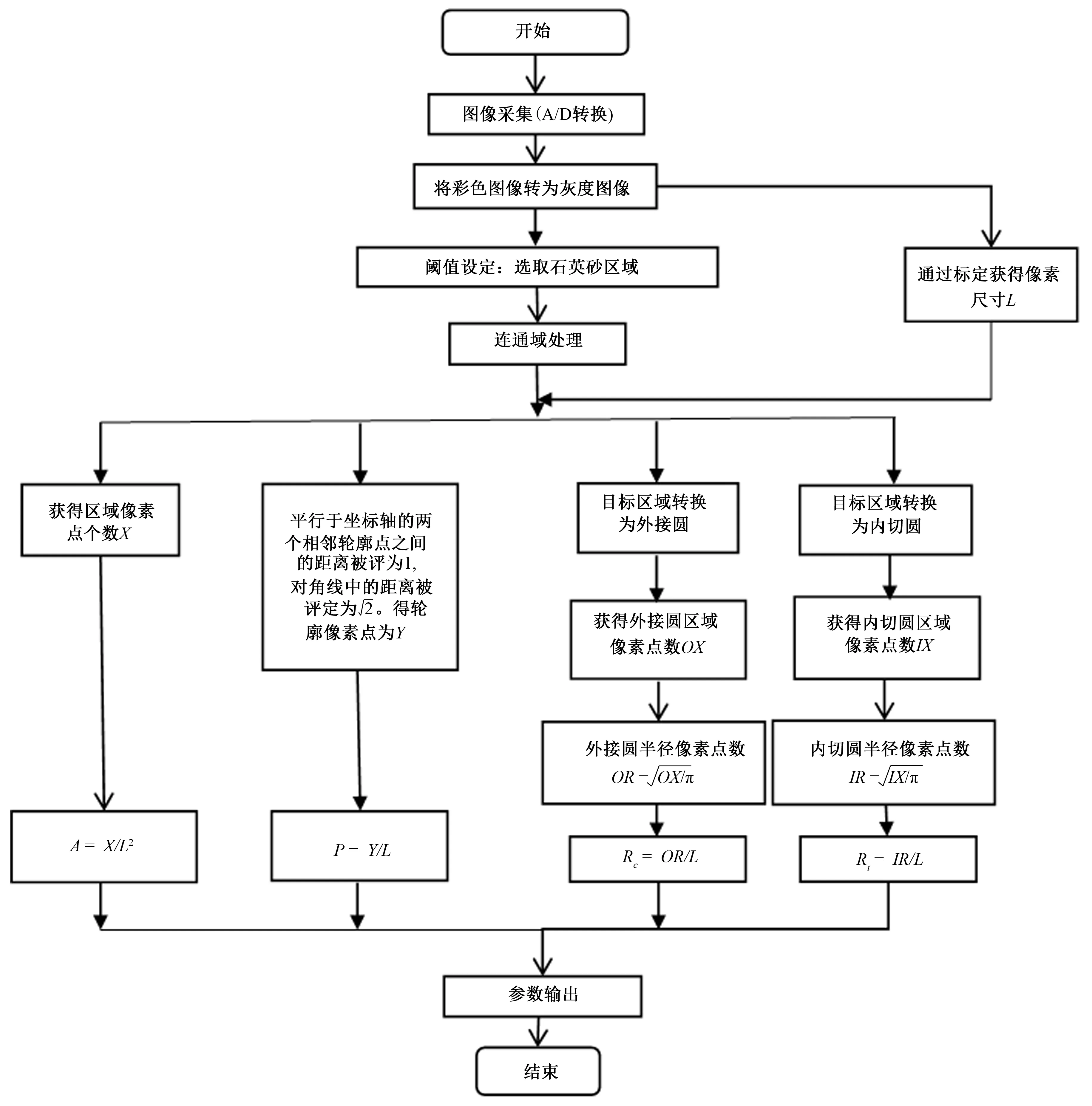
图2 砂颗粒形状参数计算框图

3.2 形状参数计算结果分析

由于石英砂颗粒形状具有随机性，因而其粒径参数与延性参数也具有随机性，因此采用样本参数的均值、标准差和变异系数来描述砂颗粒的整体特征。

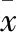
(3)

样本标准差s为：

(4)

样本变异系数Cv为：

(5)

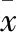
由自编程序计算得到样本的粒径参数A与P，由面积A得到砂颗粒等效直径D：

(6)

绘制砂颗粒面积波动趋势图(见图3)、砂颗粒周长波动趋势图(见图4)和砂颗粒等效直径波动趋势图(见图5)。A、P、D统计值结果见表2。

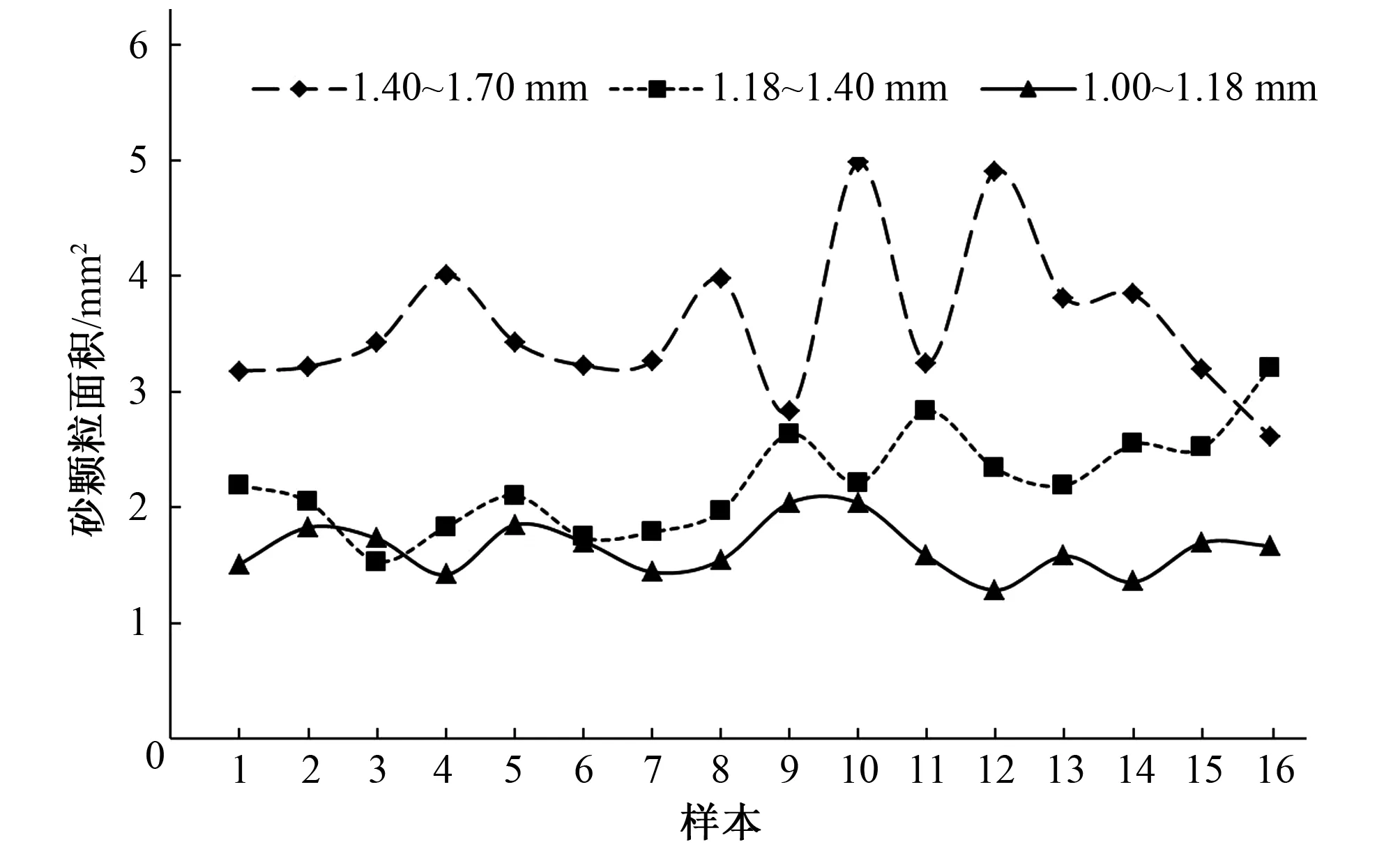
图3 砂颗粒面积波动趋势图

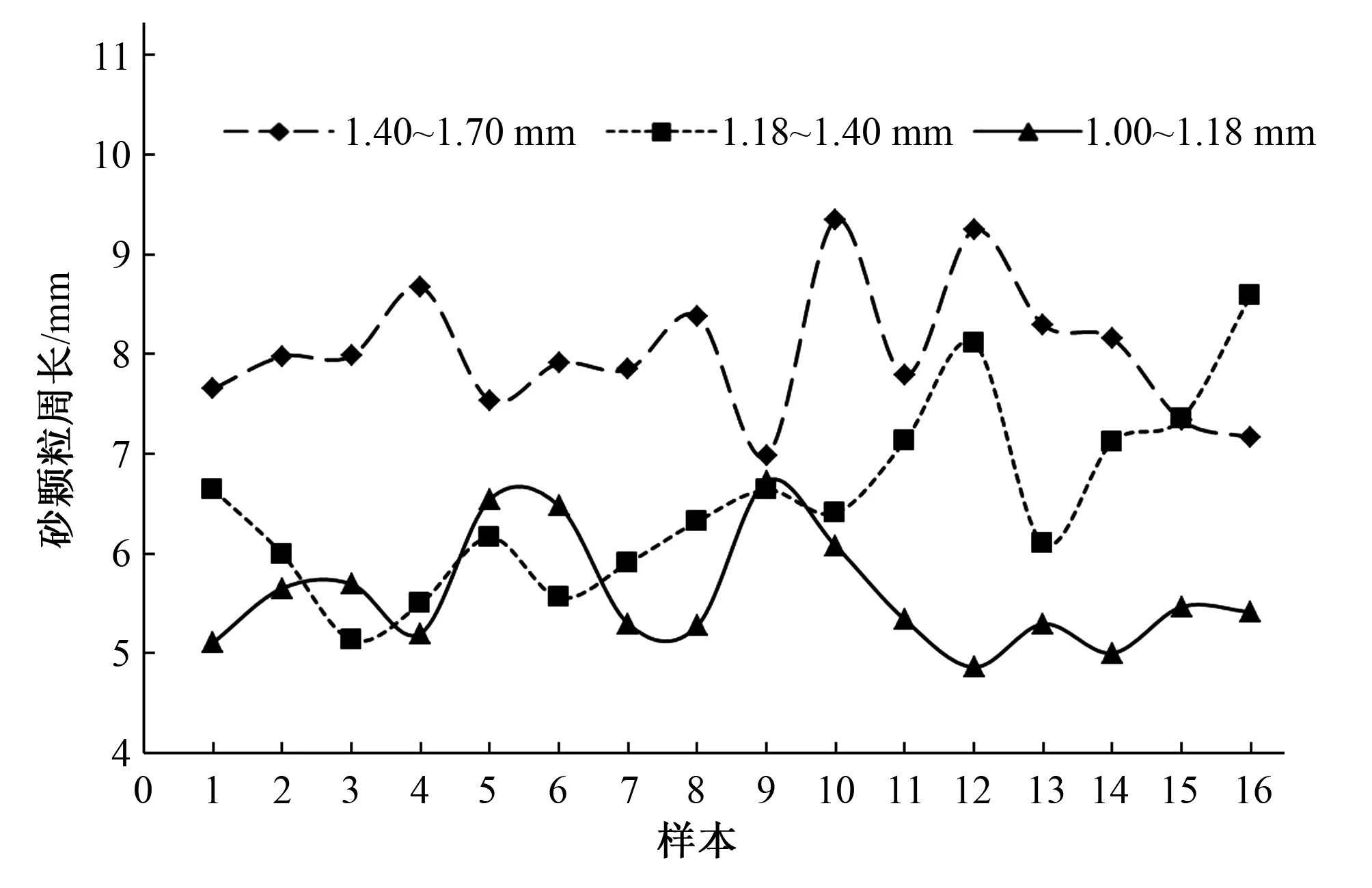
图4 砂颗粒周长波动趋势图

图5 砂颗粒等效直径波动趋势图

由图3可知，均值越大，砂颗粒面积波动幅度越大，即样本标准差越大，由表2可知，粒径为1.18～1.4 mm的石英砂，面积变异系数最大，为0.190，粒径为1.0～1.18 mm的石英砂，面积变异系数最小，为0.136。

由图4可知，粒径为1.18～1.4 mm的石英砂，周长波动幅度最大，标准差为0.908 mm，由表2知，样本变异系数也最大，为0.139。

表2 石英砂颗粒粒径参数及其统计值

由图5可知，均值越大，砂颗粒等效直径波动幅度越大，即样本标准差越大，同时由表2可知，变异系数也随均值的增加而增加，粒径为1.4～1.7 mm的石英砂，变异系数最大，为0.112。

总体而言，砂颗粒粒径参数的波动幅度较小，说明砂颗粒大小比较均匀。

由自编程序计算得到样本参数Ri和Rc，计算得到简化延长指数IA，由粒径参数A与P计算得到布拉斯谢克系数Icb，绘制砂颗粒简化延性指数波动趋势图(见图6)和布拉斯谢克系数波动趋势图(见图7)，其统计值计算结果见表3。

图6 砂颗粒简化延长指数波动趋势图

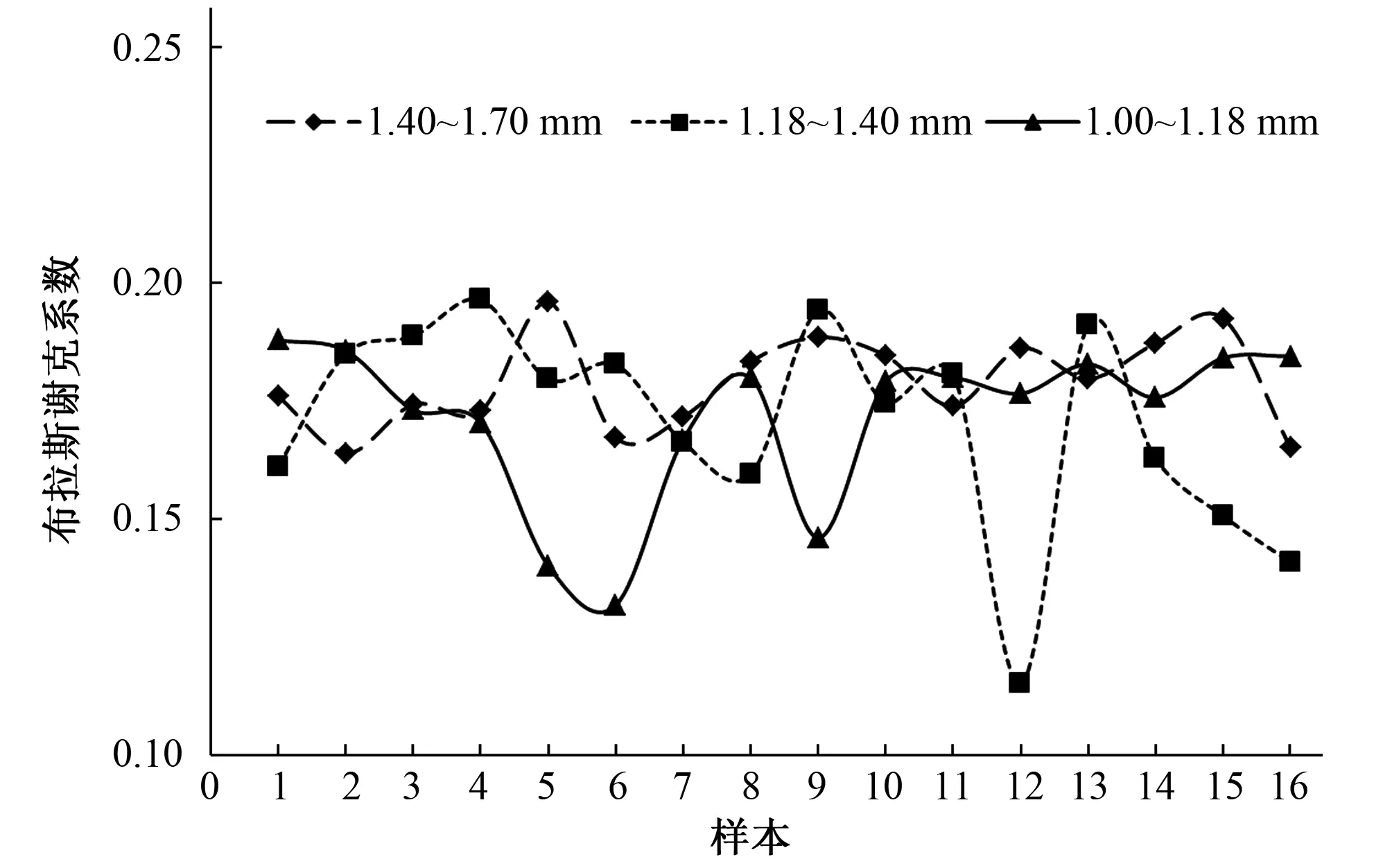
图7 砂颗粒布拉斯谢克系数波动趋势图

粒径范围延性参数最小值最大值均值标准差变异系数1.0～1.18 mmIA0.491 0.766 0.636 0.071 0.111 Icb0.132 0.188 0.172 0.017 0.096 1.18～1.4 mmIA0.440 0.710 0.606 0.072 0.119 Icb0.115 0.197 0.171 0.021 0.121 1.4～1.7 mmIA0.504 0.726 0.618 0.075 0.121 Icb0.164 0.196 0.179 0.009 0.053

由图6和图7可知，每种粒径范围砂颗粒简化延性指数波动趋势与布拉斯谢克系数波动趋势基本一致。

由表3可知，3个样本简化延长指数分别为0.636、0.606和0.618，数值十分接近，同时变异系数也比较小，最大值仅为0.121；3个样本布拉斯谢克系数分别为0.172、0.171和0.179，数值也十分接近，变异系数最大值为0.121。说明砂颗粒形状特征比较稳定，总体上颗粒形态呈扁平状，形状接近长轴与短轴比值为3∶2的椭圆形。

4 结 论

本文采用计算机图像处理技术，以粒径范围为1.0～1.18、1.18～1.4和1.4～1.7 mm的3种滤层为研究对象，每种滤层中各随机取16粒石英砂作为样本，利用自编计算机程序对微灌砂颗粒的面积、周长、外接圆半径和内切圆半径等形状系数进行了测量和分析，得出以下结论：

(1)自编程序计算了砂颗粒的面积、周长、外接圆半径、内切圆半径，根据砂颗粒的面积、周长、外接圆半径和内切圆半径计算出了简化延长指数和布拉斯谢克系数，采用样本参数的均值、标准差和变异系数来描述砂颗粒的整体特征。

(2)面积、周长和等效直径为砂颗粒的粒径参数，反映了砂颗粒的大小，是影响颗粒形状的重要参数。通过对砂颗粒粒径参数统计特征的分析，得到砂颗粒面积和周长的波动规律，结果说明砂颗粒大小比较均匀。

(3)简化延长指数和布拉斯谢克系数为砂颗粒的延性参数，采用简化延长指数和布拉斯谢克系数评价砂颗粒单元形态。砂颗粒延性参数统计分析说明，砂颗粒形状特征比较稳定，总体上颗粒形态呈扁平状，形状接近长轴与短轴比值为3∶2的椭圆形。