高速铁路地震预警阈值随机振动分析
2019-11-27李昊张鸿儒于仲洋
李昊 张鸿儒 于仲洋


摘要: 为研究地震作用下列车的动态响应和预警阈值,对车辆-轨道模型进行振动台模型试验,将试验结果与车辆-轨道数值计算模型的计算结果进行对比,对比结果基本吻合,表明数值计算模型具有一定的正确性;随后利用上述计算模型进行了地震波的频谱特性分析,结果表明,当地震波频率在1 Hz附近时,容易与车体水平向自振频率产生共振,导致列车出现轮轨分离状态。因此,采用传统脱轨指标恐无法判断列车安全运行的真實状态,将采用轮轨水平向相对位移、车轮抬升量和车体倾覆角三种脱轨指标来进行对列车地震预警阈值的确认和推导;最后提出确定高速铁路地震预警阈值的新思路。基于上述车辆轨道数值模型,挑选80条典型地震动记录,分别施加到车辆-轨道数学模型中进行时程分析计算,将计算结果中的车轮抬升量、轮轨接触点水平位移、车体倾覆角等参数与地震动峰值加速度之间的关系进行统计分析,利用随机振动原理给出地震作用下列车的地震预警阈值评价表。
关键词: 车辆-轨道模型; 振动台试验; 地震激励; 频率响应; 车轮抬升
中图分类号: U211.3; O324; P315.63 文献标志码: A 文章编号: 1004-4523(2019)05-0874-12
DOI:10.16385/j.cnki.issn.1004-4523.2019.05.016
引 言
中国的高速铁路快速发展,运营里程不断增加,至今已超过2万公里,到2025年,高速铁路将达到3.8万公里,覆盖大多数大城市。然而,中国是多地震国家,高速铁路经过的部分地区处于高烈度地震威胁之下,例如京津城际铁路、京广高速铁路、京沪高速铁路、哈大高速铁路、兰新高速铁路、西成高速铁路等,均经过该烈度地震设防区。因此,高速铁路的防震减灾问题一直受到重视。
高速铁路的防震减灾涉及到两个层次的问题:一是首先保证基础设施满足抗震设防的要求,目前已有较成熟的设计标准;二是在基础设施安全的条件下地震时列车的运行安全,目前尚无成熟的解决方案。
在过去的地震中,曾发生多起列车脱轨和颠覆事故。1976年唐山地震中,位于京山线震区的运行列车有货车28列,客车7列,其中,客车2列、货车5列发生部分车辆脱轨或倾覆[1]。1995年日本阪神地震中,共有16列列车受损,85辆车脱轨,轨道严重变形[2]。2004年日本新潟地震中,新干线列车“朱鹮325”号第8节车厢在时速200 km/h下脱轨,其中由10节车厢组成的列车中有7节车厢脱轨,列车脱轨后还继续运行了1600 m。2010年台湾高雄地震中,造成一列北上列车的一节车厢脱轨[3]。
为解决地震对高速铁路运行安全的威胁,除了进行高速铁路结构的抗震设计外,日本等国家采取了地震预警的方法,当预测的地震动达到一定阈值时,对高速列车进行减速或停车控制,从而减小列车脱轨或颠覆的危险,减少地震损失。中国部分高速铁路在建设过程中,已经预先设置了地震监测模型,以备地震预警使用;但中国在地震预警方面的研究刚刚起步,可参照的经验较少,相关参数如预警阈值等的合理性有待进一步研究和验证。
高速铁路地震预警模型主要包括三个方面的问题,第一是预测预警目的地的地震动强度,主要涉及利用早期监测到的较小的先达地震预警目的地的地震动大小,和后续产生破坏性地震动的大小;第二是确定地震作用时目的地的地震动预警阈值,与地震作用下列车的运行安全性密切相关;第三是预警信息的传输、发布和控制方法,主要包括传输发布的技术途径和控制策略和控制方式。本文主要探讨第二个问题,即预警阈值的确定。
高速铁路地震预警阈值涉及地震中列车运行的安全标准。日本是地震预警发展最早的国家,在20世纪60年代就考虑了铁路地震预警模型,其中新干线设置的预警阈值为40 gal[4],即当检测到40 gal的地震动加速度时,立即报警并控制牵引变电所停止向供电区间供电,使列车停止运行。中国学者本世纪初开始对铁路地震预警问题进行研究,北京交通大学刘林等[5]针对京沪高速铁路,以最大轨道允许横向加速度为基准,选取了60条具有代表性的地震波,通过对京沪高速铁路各类典型构筑物的大量地震响应统计分析,得到各类构筑物的动力响应系数95%概率上位值约为2.55,然后以轨道横向加速度限值(120 gal)除以动力相应系数得到预警阈值为45 gal。孙利[6]利用SI指标选取了4条典型的水平地震波分析了桥上列车地震预警阈值,得到运行速度为350 km/h的列车在以上地震波激励作用时,阈值分别为219.71,146.46,46.47,77.20 gal,取最小值,建议阈值设为40 gal。
高速铁路的地震预警阈值与地震作用下列车的动态响应、轮重减载和脱轨密切相关。文献[7-11]认为需要仔细研究地震作用下脱轨的机理,并且用更直接的参数来判别。利用5个周期长的正弦波作为地震荷载施加到轨道板上,分析了车辆轨道的动态响应,包括车轮抬升和横移。以30 mm车轮抬升量作为极限,得出了不同地震波频率所应对的、车辆安全运行的临界幅值曲线;同时,通过模拟车辆轨道全尺寸振动台试验,验证了数值分析结果,并建议车辆运行的临界幅值曲线可以应用于车辆轨道结构设计。凌亮等[12]同样利用5个周期长的正弦波对地震情况下高速列车的动力响应进行了分析,提出了两种新型的高速列车脱轨评价准则,即轮轨接触点位置和车轮抬升量。上述的研究均认为在不考虑轨道不平顺的前提下,车辆的运行速度对地震作用下车辆的运行安全边界影响不大,而地震波的频谱特性对其影响较大。Luo Xiu等[13-14]、凌亮等[15]认为地震激励频率较低时,易发生倾覆脱轨;地震激励频率较高时,易发生跳轨脱轨。Luo Xiu还对Miyamoto提出的车辆安全运行临界幅值曲线进行了讨论,并在Miyamoto研究内容的基础上提出了利用速度响应谱强度限值曲线来进行车辆轨道结构设计。徐鹏[16]、吴兴文[17]认为导致列车脱轨的原因与地震波的频率有关,且低频地震波对车辆的安全影响较大,当地震波频率在0.5-1 Hz范围内,容易与车体的上心滚摆或下心滚摆发生共振,从而影响车辆行车安全。文[18-22]对地震激励下列车运行的安全性问题用一个13自由度的半车/轨道耦合模型进行了仿真模拟,然后利用滚动振动台建立了1∶10的小型模型来进行模拟试验,最后通过车辆轨道全尺寸滚动振动台试验,验证了仿真模拟结果和车辆轨道1∶10缩尺试验结果的正确性。从而证明,在地震作用下,对列车脱轨起主导作用的是车体的侧滚运动以及轮轨蠕滑作用下的车轮横移。高速列车脱轨以“跳轨脱轨”为主要形式,且脱轨的原因与地震激励的振幅有关,与车速无关。王开云等[23]详细评述并归纳了地震作用下,列车轮轨动态安全性及列车脱轨问题,认为地震环境下,整个车辆模型、轨道模型均受地震位移或变形的影响,轮轨关系不能采用位移一致或轨道静止不动的方法,需考虑动态的、轨道结构大变形的轮轨接触。
总体看来,对地震作用下车辆轨道的动态响应、脱轨机理以及地震波幅频特性对车辆轨道运行安全的影响,已经有较一致的认识。这对于确定地震预警的阈值有一定参考价值。
考虑到地震是概率很小的偶然作用,且列车运行与地震作用可能产生耦合作用,但文[18-22]的缩尺滚动台的振动台试验表明,地震作用下的脱轨与列车速度关系不大。因此,本文對静止状态的列车-轨道在地震作用下的动态响应进行振动台试验研究,通过车辆-轨道振动台试验的试验结果来验证数值计算模型的准确性,提出一个确定地震预警阈值的初步思路,并根据典型地震波作用下的车辆轨道响应特性,给出列车地震预警阈值评价表。
1 车辆-轨道模型振动台模型试验
1.1 试验概况 试验在中国建筑科学研究院抗震实验室进行。试验模型各部件从上往下依次为车体、转向架 、钢轨、扣件、轨道板、振动台。振动台模型示意图如图1(a)所示。车厢采用角型钢和钢板围焊而成,车体底座采用框格箱体结构,框格由横向与纵向的矩形钢管拼焊而成,车体与转向架之间通过两侧旁撑支撑和心盘支撑进行焊接。轨道板为中国自主研发的CRTSⅢ型轨道板,如图1(b)所示。转向架采用石家庄车辆厂国产K2型转向架,如图1(c)所示。钢轨为60 kg/m轨,扣件采用WJ-8b型扣件,如图1(d)所示。为了较好地模拟半车体质量,采用添加配重块的方法进行车体质量模拟,如图1(e)所示。对轨道板板面进行钻孔设计,采用14根直径为30 mm的钢螺栓将轨道板锚固在振动台中央,使车辆-轨道模型可以随振动台同步振动。车辆轨道模型尺寸参数如表1所示。
考虑到在施加地震荷载的过程中容易发生车体摇摆和倾覆现象,故在试验模型周围架设黄色防倒塌钢架,如图2所示,确保试验安全进行。同时为防止车辆在振动过程中在轨道上滑动,采用两根直径为5 mm的钢弦将车体中部的前后端拴在防倒塌钢架的前后中柱上。
1.2 试验方案
试验采用WP-S型位移计(精度1/100 mm)量测车轮抬升量和轮轨水平相对位移,位移计布置如图3所示。采用直角应变花,通过组全桥的方式量测轮轨之间的垂向力和水平向力,图4为应变片组桥示意图。为方便轮轨力的量测和读取,试验开始前应按照规范《TBT2489-2016》[24]所提方法对轨道的垂向力和水平向力进行标定,标定方法如图5所示。
1.3 加载工况
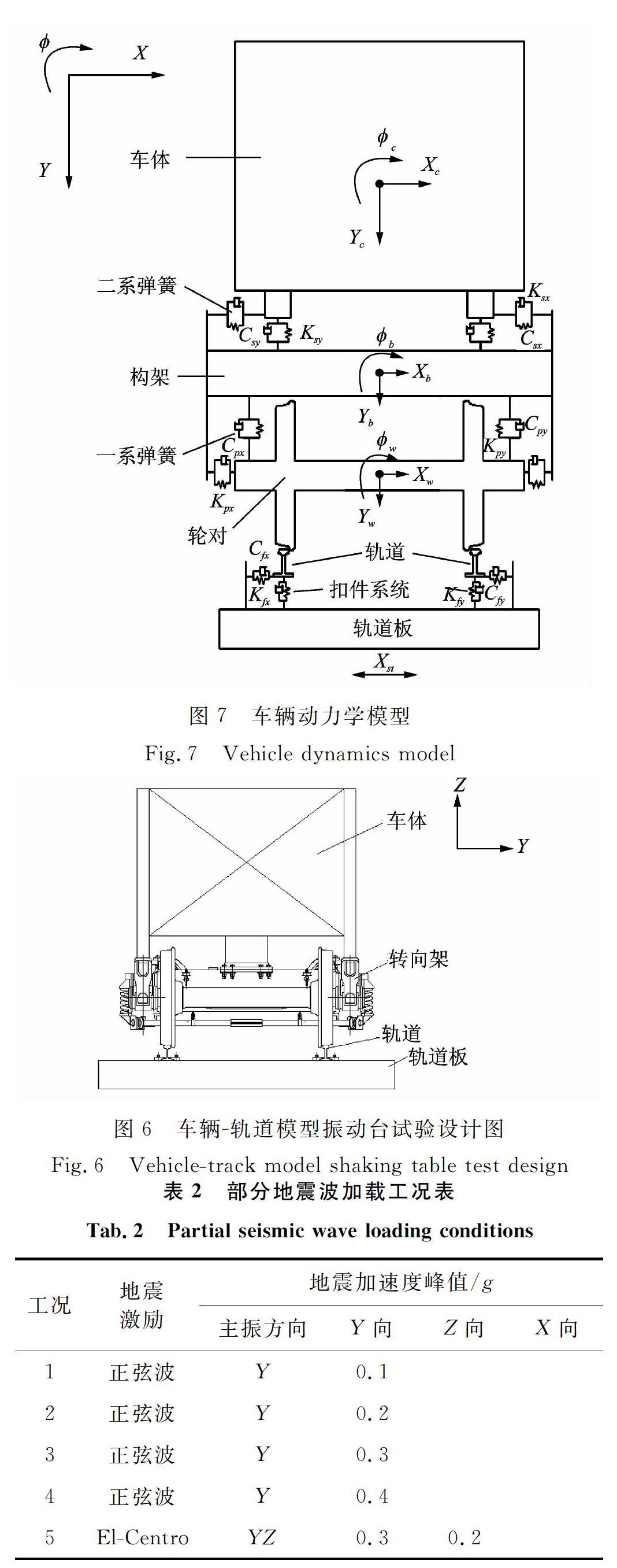
对车辆-轨道模型施加的地震波分别为5个周期的正弦地震波、El-Centro波、Kobe波和人工波,每条地震波均分级加载,其中地震波输入方向为水平向的共24个工况,输入方向为双向的共1个工况,即水平向、垂向同时施加El-Centro地震波,总计25个工况。地震波施加方向分别为Y方向和Z方向,其中Y方向为水平向、Z方向为垂向,试验模型设计简图如图6所示,限于篇幅原因,只列出部分工况如表2所示。
2 车辆-轨道模型数值模型
2.1 车辆-轨道模型 模型从上往下分别为车体-转向架-轮对-钢轨-扣件-轨道板。根据车辆-轨道动力学理论,高速列车的单节车辆可简化为由车体、构架、轮对和一、二系弹簧组成,轮对和构架间用一系弹簧连接,而车体与构架则用二系弹簧连接。钢轨与轨道板之间建立了弹簧阻尼单元来模拟扣件。
车辆模型包含1个车体、1个构架、1个轮对共3个刚体结构,各刚体考虑横向、垂向、侧滚这3个方向的自由度,整个车辆模型由9个自由度的多刚体模拟;另外,一、二系弹簧以及扣件模型均采用Pro Cartesian弹簧单元进行模拟,地震荷载从轨道板底部输入,整个计算模型如图7所示。
在动力学模型中,车轮内径为845 mm,外径为915 mm,厚度为145 mm,钢轨采用标准60轨,轨高176 mm,下宽150 mm,上宽73 mm,腰厚16.5 mm。钢轨间距根据规范取为1435 mm,车轮之间的轮轴为100 mm。轨道板铺于钢轨之下,长2.5 m,厚度为260 mm,为混凝土结构。钢轨、轨道板和扣件模型均采用线弹性本构模型,参数如表3所示。轨道上部结构各部件动力学参数如表4所示。
2.2 轮轨接触设置
模型中采用施加接触对的方式模拟轮轨间的相互作用,轮轨空间动态接触力模型包括轮轨切向力计算模型和轮轨法向力计算模型两部分。轮轨切向力则采用“罚函数”的计算方法,接触面的摩擦系数设为0.3;轮轨法向力表征的是轮轨接触处法向荷载与局部变形之间的关系,采用 “Hertz”接触的接触方法对模型进行分析,轮轨接触示意图如图8所示。
(3)2.3 数值模型的验证
上述车辆轨道模型参数均与振动台模型试验一致。拟通过和振动台模型试验结果相对比,来验证本文所建立的车辆-轨道计算模型的准确性。
将正弦地震波水平向施加到车辆轨道动力学模型底部,进行地震时程分析,分别绘出车轮抬升量、轮轨水平方向接触力和轮轨垂直方向接触力的动态响应随地震激励时间的变化规律,并与车辆轨道振动台模型试验结果进行对比分析。
通过对比,如图9所示,发现数值计算结果与振动台模型试验结果基本一致。虽细节处存在一定差异,但从两种结果的周期和峰值来看,数值计算结果与试验结果相吻合,表明车辆-轨道数值计算模型完美的模拟了试验的真实状态。
3 正弦波作用下模型的响应特征分析
地震波的强度、频率以及其持续的时间等都对车辆-轨道结构有着重要的影响,而地震波频谱特性对其的影响尤为显著。为了研究不同频谱地震波作用下车辆轨道的脱轨机理,分别采用时程分析和频域分析两种方法对车辆-轨道动力学模型进行不同地震波频率作用下的动态响应分析。
地震波采用单频率的加速度正弦波,其加速度峰值分别为0.1g,0.15g,0.2g,0.25g,0.3g,0.35g,根据车辆系统动力学理论可知,车辆系统的刚体模态主要集中在低频范围内,故选取频率范围为0.1-5 Hz,车辆-轨道数值计算模型参数保持不变,对其进行分析。将时程分析和频域分析所计算的结果进行统计汇总,分别得出两种算法下的轮轨水平向力、轮轨垂向力、车轮抬升量的频率响应关系图,如图10-12所示。
由图10-12可知,车辆-轨道动力学模型的时程分析结果与频域分析计算结果的变化规律基本接近,两种分析方法显示各脱轨指标均在1 Hz附近出现响应峰值,在高频范围内(大于1.5 Hz)各脱轨指标随着地震波频率的增加而趋于平稳。
为进一步探究地震波幅频特性对车辆系统的影响,对动力学模型进行自振频率分析,表5为车辆各部件自震频率计算结果。由表5可知,当地震波频率为0.91 Hz时,此时地震波的频率与车体水平向自振频率一致,较易产生共振,从而导致各脱轨指标在地震波频率为1 Hz附近达到响应峰值。
综上所述,地震波具有一定的复杂性,高速铁路运行安全除了与地震波强度有关外,还与地震波频率有重要的关系,尤其当地震波频率在1 Hz附近时,很容易与车体水平向自振频率发生共振,使车辆水平向滚摆运动加剧,极有可能出现轮轨分离状态,从而导致列车脱轨。当列车出现轮轨分离状态时,采用传统的脱轨指标如脱轨系数(Q/P)、轮重减载率(ΔP/P)等指标,可能无法准确地判断列车运行安全的真实状态。
4 地震作用下轮轨动力响应和地震预警阈值4.1 确定地震预警阈值的初步思路
在铁路设计建造和养护维修中常利用脱轨系数、轮重减载率等来评价列车在列车正常运行状态的安全,而养护标准中的脱轨系数等限值与脱轨极限尚有一段差距,例如,脱轨系数养护维修限值为0.8,《国际铁路联盟UIC规程》规定脱轨系数限值为Q/P≤1.2,由此可以判断出列车正常运行状态下脱轨系数存在相当大的安全冗余量。因此,可以考虑利用列车运行状态之间的安全冗余作为确定地震预警阈值的一个途径,其中地震作用假定可以按列车静止状态考虑。这一途径的优势是对于静止状态的列车-轨道在地震作用下的动态响应可以通过振动台试验予以检验;其主要缺陷实际上是,列车运行与地震作用可能产生耦合作用,但Nishimura[18-22]等的缩尺滚动台的振动台试验表明,地震作用下的脱轨与列车速度关系不大。因此,可以将上述路径作为确定地震预警阈值的初步近似。
本文拟在数值模拟基础上,提出地震预警阈值的初步建议,主要包括:
(1)将地震作用下列车运行状态看作为列车在不平顺的轨道上运行和地震作用下列车在光滑的轨道上运行这两种状态的叠加,地震激励下列车在光滑的直线轨道上运行时的车轮抬升量、轮轨接触点水平相对位移以及车体的倾覆角可近似等效于地震激励下列车静止状态时的车轮抬升量、轮轨接触点相对水平位移以及车体的倾覆角的值,则采用地震作用下列车静态的方法计算上述3种脱轨指标。
(2)采用80条典型地震记录,通过数值模拟,确定地震作用下静止状态列车的车轮抬升量、轮轨接触点水平位移、车体倾覆角等参数与地震动峰值加速度之间的关系,从而对其进行随机振动分析,并利用3种脱轨指标给出高速铁路的列车地震预警阈值的建议值。
4.2 车辆轨道模型随机振动分析
为研究列车地震预警阈值,继续采用上述车辆轨道动力学数值模型,通过选取80条典型的地震波对车辆-轨道模型进行动力响应分析,对80条地震波加速度時程曲线进行规格化处理,按0.01g的增量分别将各地震波加速度峰值调整为0.01g,0.02g,…,0.09g,0.1g,图13为部分地震波加速度峰值为0.1g时的加速度时程曲线。
把作用于车辆-轨道模型的地震动过程作为随机过程,从统计概率上推断车辆-轨道模型动力性能的理论,即为随机振动理论。随机振动理论大体可概括如下:作为结构分析的最终目的——评价安全度的方法,是要在统计概率上进行结构安全度的定量评价。以往的确定论方法过于依赖设计者的经验,因而从理论和经验的妥协出发而拟出的“现行安全率”曾是安全度评价的位移依据。而随机振动理论认为,能够利用产生破坏的概率Pf或者不发生破坏的概率,即可靠性Ps=1-Pf代替上述安全率来评价安全度。讨论计算分析车辆-轨道模型对于地震荷载的安全度,即其动力可靠性,可归结为从理论上计算出其首次偏移概率。
4.3 动力可靠度
综上所述,采用车轮抬升量,轮轨接触点的相对水平位移以及车体倾覆角作为地震作用下列车的脱轨指标可以清晰地记录轮轨间的相对位置和列车的脱轨状态,通过随机振动分析将地震波加速度峰值为0.01g-0.1g,即地震预警阈值时,首次偏移概率为2.5%的各脱轨指标统计如表6所示。
5 结 论
对车辆-轨道模型进行振动台模型试验,将试验结果与车辆-轨道数值计算模型的计算结果进行对比;随后,利用车辆-轨道数值计算模型,对地震作用下车辆-轨道模型进行分析计算,得出主要结论如下:
(1)将数值模拟结果与车辆轨道模型振动台试验结果对比分析,发现数值计算结果与振动台模型试验结果基本一致,虽细节处存在一定差异,但从两种结果的周期和峰值来看数值计算结果与试验结果相吻合。
[11] Lida K, Suzuki M, Miyamoto T, et al. Development of a lateral damper to improve the running safety of railway vehicles during an earthquake[J]. Quarterly Report of RTRI, 2012,53(1):34-40.
[12] 凌 亮, 肖新標, 吴 磊, 等. 地震激励下高速列车动态响应与运行安全边界研究[J]. 铁道学报,2012,34(10):16-22.
Ling Liang, Xiao Xinbiao, Wu Lei, et al. Research on dynamic response and operational safety boundary of high-speed train under earthquake excitation[J]. Journal of the China Railway Society, 2012,34(10):16-22.
[13] Luo Xiu.Study on methodology for running safety assessment of trains in seismic design of railway structures [J]. Soil Dynamics and Earthquake Engineering, 2005,25(2):79-91.
[14] Luo Xiu,Miyamoto T.Method for running safety assessment of railway vehicles against structural vibration displacement during earthquakes[J]. Quarterly Report of RTRI, 2007,48(3):129-135.
[15] 凌 亮, 肖新标,吴 磊,等.地震波频谱特性对高速列车动态脱轨行为的影响[J]. 工程力学,2013,30(1):384-393.
Ling Liang, Xiao Xinbiao, Wu Lei, et al. Influence of spectral characteristics of seismic waves on dynamic derailment behavior of high-speed trains[J]. Engineering Mechanics, 2013,30(1):384-393.
[16] 徐 鹏. 列车-轨道-路基耦合振动及地震条件下行车安全性分析[D]. 成都:西南交通大学, 2011.
Xu Peng. Analysis of train-track-subgrade coupled vibration and seismic conditions for down vehicle safety[D]. Chengdu: Southwest Jiaotong University, 2011.
[17] 吴兴文.地震条件下车辆脱轨安全性研究[D]. 成都:西南交通大学, 2016.
Wu Xingwen. Research on vehicle derailment safety under earthquake conditions[D]. Chengdu: Southwest Jiaotong University, 2016.
[18] Nishimiira K, Terumichi Y, Morimura T, et al. Development of vehicle dynamics simulation for safety analyses of rail vehicles on excited tracks[J]. Journal of Computational and Nonlinear Dynamics,2009,4(1):1-9.
[19] Nishimura K,Terumichi Y, Morimura T, et al. Experimental study on the vehicle safety by earthquake track excitation with 1/10 scale vehicle and roller rig [J]. Journal of System Design and Dynamics, 2010, 4(1): 226-238.
[20] Nishimura K,Terumichi Y,Morimura T,et al. Analytical study on the safety of high speed railway vehicle on excited tracks[J]. Journal of System Design and Dynamics, 2010, 4(1):211-225.
[21] Kazuhiko NISHIMURA, Yoshiaki TERUMICHI, Tsutomu MORIMURA, et al. Experimental study on the vehicle safety by earthquake track excitation with 1/10 scale vehicle and roller rig[J]. Journal of System Design and Dynamics, 2010,4(1):226-238.
[22] Kazuhiko Nishimura, Yoshiaki T, Tsutomu M, et al. Using full scale experiments to verify a simulation used to analyze the safety of rail vehicles during large earthquakes[J]. Journal of Computational and Nonlinear Dynamics, 2015,10:1-9.
[23] 王开云,王少林,杨久川,等.地震环境下铁路轮轨动态安全性能及脱轨研究进展[J].地震工程与工程振动,2012,32(6):82-94.
Wang Kaiyun, Wang Shaolin, Yang Jiuchuan, et al. Research progress on dynamic safety performance and derailment of railway wheel and rail in earthquake environment[J]. Earthquake Engineering and Engineering Vibration, 2012, 32(6): 82-94.
[24] 国家铁道局.高速铁路设计规范(试行)(TB10621-2009)[S]. 北京:中国铁道出版社, 2010.
State Railways Adminstration. Design specification for high speed railway (Trial)(TB10621-2009)[S]. Beijing: China Railway Publishing House, 2010.
Abstract: In order to study the dynamic response and early warning threshold of vehicles, the shaking table test of the vehicle-track model is carried out, and the test results are compared with the calculation results of the vehicle-track numerical calculation model. The comparison results are basically consistent which indicates that the numerical calculation model is correct. Subsequently, the spectral characteristics of seismic waves are analyzed, and the results show that when the seismic wave frequency is near 1Hz, it is easy to resonate with the horizontal natural frequency of the vehicle body. Therefore, appropriate measures should be taken in vehicle design to keep the natural vibration frequency of the vehicle system away from the lower frequency domain. Last, a new idea for determining the earthquake early warning threshold of high-speed railway is proposed. Based on the vehicle-track numerical model, 80 typical ground motion records are selected and applied to the vehicle-track mathematical model for time-history analysis and calculation. The parameters such as wheel lift, wheel-rail contact point horizontal displacement, vehicle body overturning angle and ground motion peak acceleration are calculated. The relationships between them are statistically analyzed. Finally, the stochastic vibration theory is used to give an earthquake warning threshold evaluation table for the vehicles.
Key words: vehicle-track model; shaking table test; seismic excitation; frequency response; wheel lift
作者簡介: 李 昊(1988-),男,博士研究生。电话: 15120072305; E-mail: 14115281@bjtu.edu.cn
