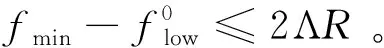非光滑约束优化的改进水平束方法

唐春明,王贞贞,郑海艳

(广西大学 数学与信息科学学院, 广西 南宁 530004)

0 引言

研究求解如下非光滑约束优化问题：

fmin:=min{f(x):c(x)≤0,x∈X},

(1)

其中,f,c:Rn→R均为凸函数, 但不一定连续可微,X⊆Rn为非空紧凸集。

形如(1)的优化问题在最优控制、联合机会约束规划、随机规划、能源问题和物流选址等领域有着广泛应用[1-3]。束方法是求解非光滑优化问题最有效的方法之一, 主要通过多面体模型近似目标函数，每步迭代求解一个二次规划子问题，是一种稳定化的割平面法，如文献[4-8]。束方法主要包括邻近束方法、水平束方法和信赖域束方法等。求解约束优化问题(1)的束方法又可细分为罚函数法[5], 改进函数法[9-10]和滤子法[11]等。改进函数法考虑如下改进函数：

h(x;fmin)=max{f(x)-fmin,c(x)},

(2)

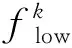
(3)

子问题(3)采用传统的欧氏范数作为距离函数, 为了充分利用可行集的几何结构, 提高计算效率, 可考虑用广义距离函数代替欧氏距离。KIWIEL[12]提出了基于Bregman距离函数的邻近束方法, 并证明了算法的全局收敛性。BEN-TAL等[13]提出了非欧氏限制记忆水平束方法, 允许根据可行集的几何形状调整方案, 得到的迭代复杂度与可行集的维数无关。欧小梅等[14]提出了基于Bregman距离的双稳定束方法。

本文针对非光滑约束优化问题(1), 对文献[10]的工作进行推广, 提出了基于Bregman距离的水平束方法, 将传统欧氏距离推广到广义Bregman距离, 从而可充分利用可行集的几何结构, 提升计算效率。该方法利用多面体模型近似原问题的目标函数和约束函数, 并引入改进函数作为最优性判别函数。最后证明了算法的全局收敛性并分析了迭代复杂度。

1 改进水平束方法的算法设计

定义Bregman距离函数[12-13]：

(4)

其中,ω(x)是可微的强凸函数, 强凸系数为σ>0, 即：

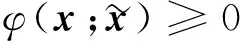
基于广义距离函数(4), 定义X的“直径”如下：

(5)

该直径基于Bregman距离函数，是传统欧式距离下定义的直径的推广。

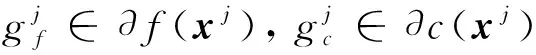
进而定义f(x),c(x)在第k次迭代的多面体模型：

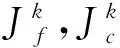
文献[10]将改进函数作为最优性判别函数, 并采用如下方式记录改进函数当前的最小值和相应的迭代点：

(6)

(7)

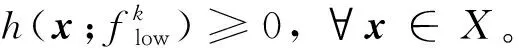
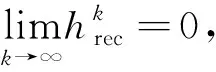
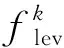
本文采用Bregman距离函数代替子问题(3)中的欧氏距离, 得到新型子问题如下：

(8)

下面将给出子问题(8)的最优解的一些重要性质, 其在束管理中起到重要的作用。

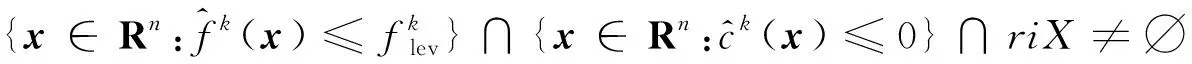
(9)

此外, 聚集线性化:

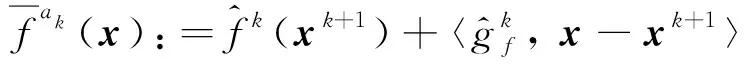
(10)

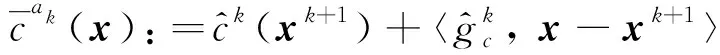
(11)

同时, 有:

(12)

证明：记iX是集合X的指示函数, 即当x∈X时, 有iX(x)=0;当x∉X时,iX(x)=+∞, 且有∂iX(x)=NX(x),∀x∈X, 其中NX(x)为X在x处的法锥。因此子问题(8)可等价为：

(13)

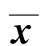
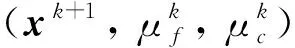
算法1(改进水平束方法)步骤如下：

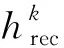
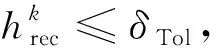
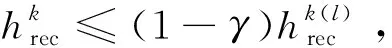
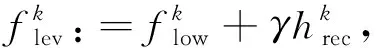
Step5(可行性检测)：如果Xk为非空集, 则转到step 6; 否则, 转step 7。

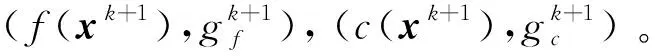
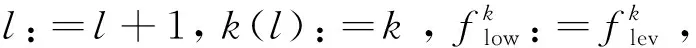
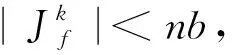
Step9(循环)：令k:=k+1, 返回step 1。

2 收敛性与复杂度分析

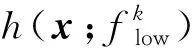
下面引理给出相邻两个迭代点距离的下界, 其说明连续的迭代点是不相同的。

引理3[10]在算法1的第k次迭代中下列关系成立：

下面将证明每一个循环Kl中的迭代次数是有限的。

引理4算法1的第l个循环中的迭代指标k(k∈Kl)满足：

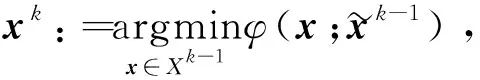
(14)

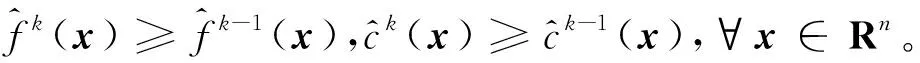
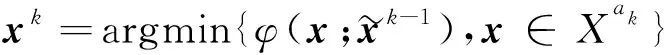
(15)

从而：

…

对上述求和得：

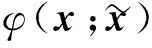
于是：

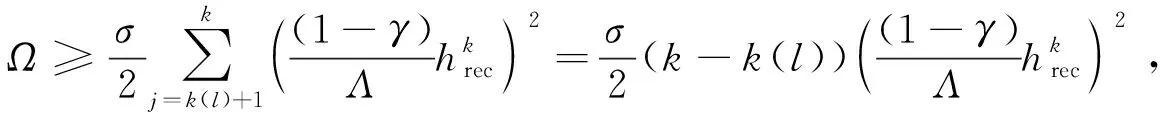
从而有：

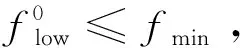
当初始下界通过如下方式选择：

(16)

则下面的命题给出了在一个循环中迭代次数的最大数目的上界。

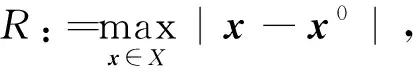
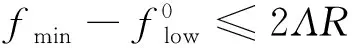
(17)

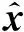
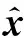
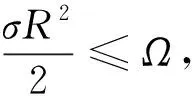
结合引理4可以得到式(17)的第二个不等式。

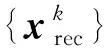
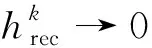
类似于文献[10]的定理2, 给出如下的计算复杂度结果。